六年级上册数学讲义-小升初培优:第07讲 立体图形体积(解析版)全国通用
文档属性
| 名称 | 六年级上册数学讲义-小升初培优:第07讲 立体图形体积(解析版)全国通用 |  | |
| 格式 | doc | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 09:58:04 | ||
图片预览

文档简介
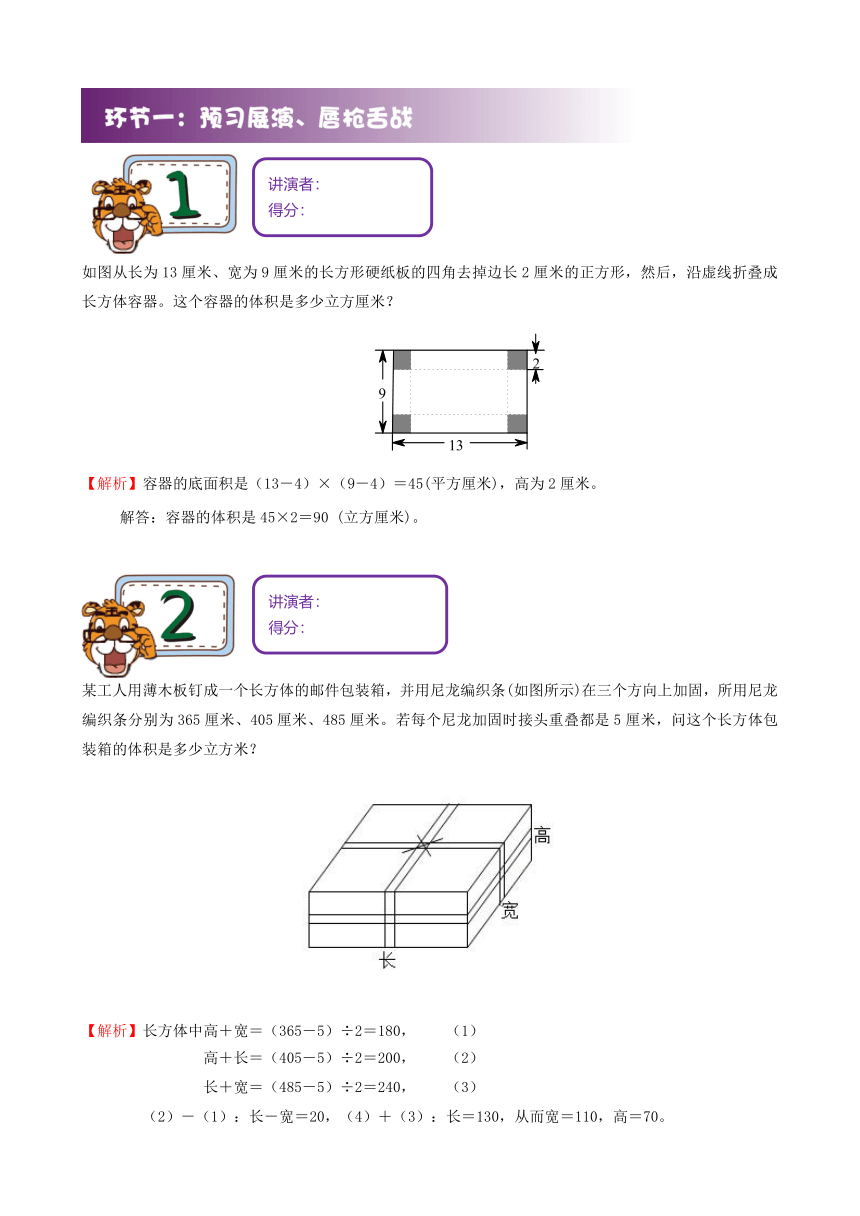
第七讲 立体图形体积
如图从长为13厘米、宽为9厘米的长方形硬纸板的四角去掉边长2厘米的正方形,然后,沿虚线折叠成长方体容器。这个容器的体积是多少立方厘米?
【解析】容器的底面积是(13-4)×(9-4)=45(平方厘米),高为2厘米。
解答:容器的体积是45×2=90 (立方厘米)。
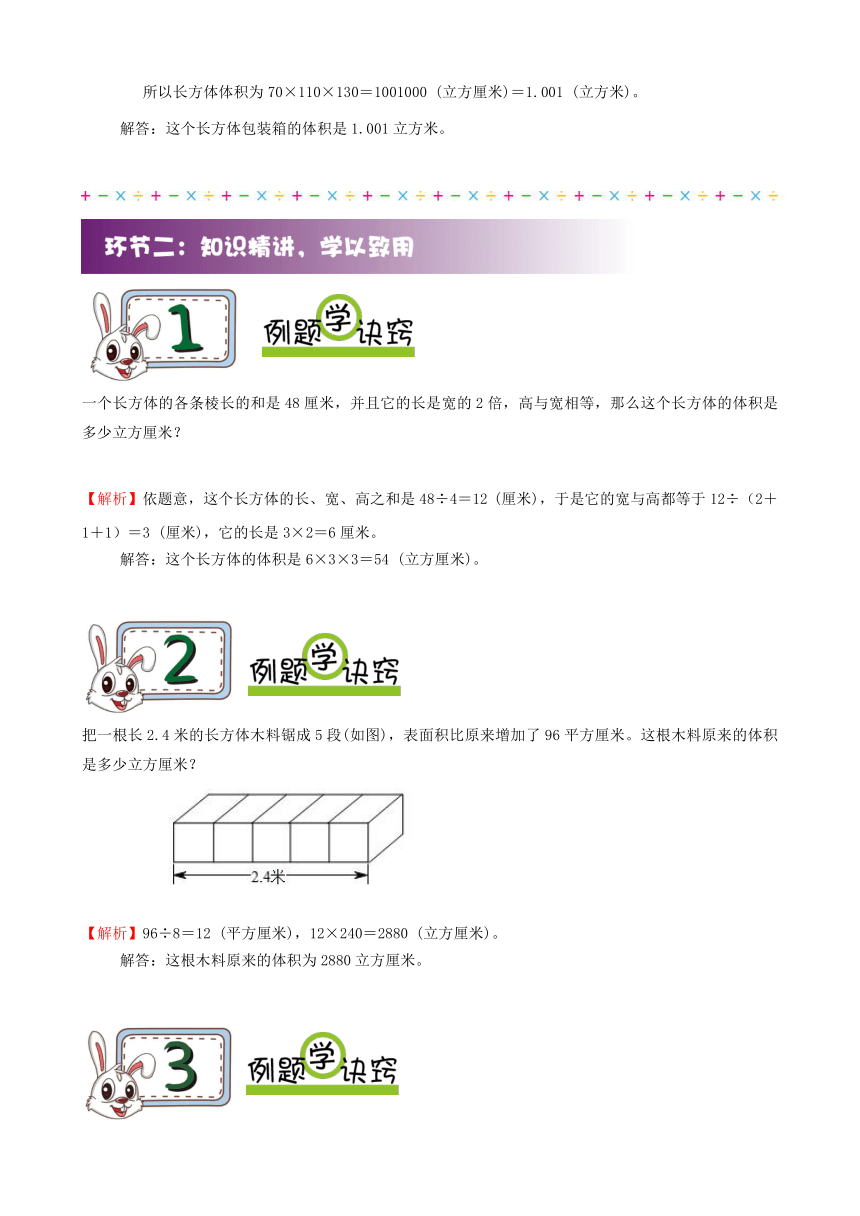
某工人用薄木板钉成一个长方体的邮件包装箱,并用尼龙编织条(如图所示)在三个方向上加固,所用尼龙编织条分别为365厘米、405厘米、485厘米。若每个尼龙加固时接头重叠都是5厘米,问这个长方体包装箱的体积是多少立方米?
【解析】长方体中高+宽=(365-5)÷2=180, (1)
高+长=(405-5)÷2=200, (2)
长+宽=(485-5)÷2=240, (3)
(2)-(1):长-宽=20,(4)+(3):长=130,从而宽=110,高=70。
所以长方体体积为70×110×130=1001000 (立方厘米)=1.001 (立方米)。
解答:这个长方体包装箱的体积是1.001立方米。
一个长方体的各条棱长的和是48厘米,并且它的长是宽的2倍,高与宽相等,那么这个长方体的体积是多少立方厘米?
【解析】依题意,这个长方体的长、宽、高之和是48÷4=12 (厘米),于是它的宽与高都等于12÷(2+1+1)=3 (厘米),它的长是3×2=6厘米。
解答:这个长方体的体积是6×3×3=54 (立方厘米)。
把一根长2.4米的长方体木料锯成5段(如图),表面积比原来增加了96平方厘米。这根木料原来的体积是多少立方厘米?
【解析】96÷8=12 (平方厘米),12×240=2880 (立方厘米)。
解答:这根木料原来的体积为2880立方厘米。
一个长方体的宽和高相等,并且都等于长的一半(如图)。将这个长方体切成12个小长方体,这些小长方体的表面之和为600平方分米。求这个大长方体的体积。
【解析】设大长方体的宽(高)为a分米,则长为2a,右(左)面积为a?,其余面的面积为2a?,根据题意,
2×2a?+8a?+6×2a?=600, 所以a?=25,a=5。
大长方体的体积=2×5×5×5=250 (立方分米)。
一个长方形水箱,从里面量长40厘米,宽30厘米,深35厘米。原来水深10厘米,放进一个棱长20厘米的正方形铁块后,铁块的顶面仍然高于水面,这时水面高多少厘米?
【解析】根据长方体的体积公式可以求出水箱内水的体积;放进去棱长20厘米的正方形铁块后,铁块的顶面仍然高于水面,说明这时候水的体积没变,但是水箱的底面积变小了,利用h=V÷S,从而可以求出水此时的高度,由此解决问题。水箱的底面积是40×30=1200(平方厘米),水的体积是1200×10=12000(立方厘米),铁块的底面积是20×20=400(平方厘米),放入铁块后,水箱的底面积变成了1200-400=800(平方厘米),这时水面高12000÷800=15(厘米)。
解答:这时水面高为15厘米。
有大、中、小三个正方形水池,它们的内边长分别是6米、3米、2米。把两堆碎石分别沉没在中、小水池的水里,两个水池的水面分别升高了6厘米和4厘米。如果将这两堆碎石都沉没在大水池的水里,大水池的水面升高了多少厘米?
【解析】把碎石沉没在水中,水面升高所增加的体积,就等于所沉入碎石的体积。因此,沉入水池中碎石的体积是3×3×0.06=0.54(米?),而沉入小水池中碎石的体积是2×2×0.04=0.16(米?),这两堆碎石的体积一共是0.54+0.16=0.7(米?)。把它们都沉入大水池里,大水池水面升高所增加的体积也就是0.7米3。大水池的底面积是6×6=36(米?)。所以水面升高了0.7÷36=(厘米)。
解答:大水池的水面升高了厘米。
一根长方体木料,体积是0.078立方米。已知这根木料长1.3米,宽为3分米,高该是多少分米?至慧兔把高错算为3分米,那么,这根木料的体积要比0.078立方米多多少?
【解析】0.078÷(1.3×0.3)=0.2(米),0.2米=2分米;
1.3×0.3×0.3-0.078=0.039(立方米)。
解答:这根木料的高是2分米;算错后,这根木料的体积比0.078立方米多0.039立方米。
有一个长方体的盒子,从里面量长40厘米,宽12厘米,高7厘米,在这个盒子里放长5厘米,宽4厘米,高3厘米的长方体木块。最多可放多少块?
【解析】下图表明3×4的长方形可以填满7×12的长方形。于是5×3×4的长方体可以填满40×7×12的长方体,即盒子中最多可放这种长方体40×7×12÷(5×3×4)=56(个)。
长方体的表面积是33.66平方分米,其中一个面的长是2.3分米,宽是2.1分米,它的体积是立方分米?
【解析】长方体的高是(33.66-2.1×2.3×2)÷2÷(2.1+2.3)=(分米)。
解答:长方体的体积是2.1×2.3×=(立方分米)。
约翰·何顿·康威(John Horton Conway,1937年12月26日-),生于英国利物浦,数学家,活跃于有限群的研究、趣味数学、纽结理论、数论、组合博弈论和编码学等范畴。康威年少时就对数学很有强烈的兴趣:四岁时,其母发现他背诵二的次方;十一岁时,升读中学的面试,被问及他成长后想干什么,他回答想在剑桥当数学家。后来康威果然于剑桥大学修读数学,现为普林斯顿大学的教授。
如图从长为13厘米、宽为9厘米的长方形硬纸板的四角去掉边长2厘米的正方形,然后,沿虚线折叠成长方体容器。这个容器的体积是多少立方厘米?
【解析】容器的底面积是(13-4)×(9-4)=45(平方厘米),高为2厘米。
解答:容器的体积是45×2=90 (立方厘米)。
某工人用薄木板钉成一个长方体的邮件包装箱,并用尼龙编织条(如图所示)在三个方向上加固,所用尼龙编织条分别为365厘米、405厘米、485厘米。若每个尼龙加固时接头重叠都是5厘米,问这个长方体包装箱的体积是多少立方米?
【解析】长方体中高+宽=(365-5)÷2=180, (1)
高+长=(405-5)÷2=200, (2)
长+宽=(485-5)÷2=240, (3)
(2)-(1):长-宽=20,(4)+(3):长=130,从而宽=110,高=70。
所以长方体体积为70×110×130=1001000 (立方厘米)=1.001 (立方米)。
解答:这个长方体包装箱的体积是1.001立方米。
一个长方体的各条棱长的和是48厘米,并且它的长是宽的2倍,高与宽相等,那么这个长方体的体积是多少立方厘米?
【解析】依题意,这个长方体的长、宽、高之和是48÷4=12 (厘米),于是它的宽与高都等于12÷(2+1+1)=3 (厘米),它的长是3×2=6厘米。
解答:这个长方体的体积是6×3×3=54 (立方厘米)。
把一根长2.4米的长方体木料锯成5段(如图),表面积比原来增加了96平方厘米。这根木料原来的体积是多少立方厘米?
【解析】96÷8=12 (平方厘米),12×240=2880 (立方厘米)。
解答:这根木料原来的体积为2880立方厘米。
一个长方体的宽和高相等,并且都等于长的一半(如图)。将这个长方体切成12个小长方体,这些小长方体的表面之和为600平方分米。求这个大长方体的体积。
【解析】设大长方体的宽(高)为a分米,则长为2a,右(左)面积为a?,其余面的面积为2a?,根据题意,
2×2a?+8a?+6×2a?=600, 所以a?=25,a=5。
大长方体的体积=2×5×5×5=250 (立方分米)。
一个长方形水箱,从里面量长40厘米,宽30厘米,深35厘米。原来水深10厘米,放进一个棱长20厘米的正方形铁块后,铁块的顶面仍然高于水面,这时水面高多少厘米?
【解析】根据长方体的体积公式可以求出水箱内水的体积;放进去棱长20厘米的正方形铁块后,铁块的顶面仍然高于水面,说明这时候水的体积没变,但是水箱的底面积变小了,利用h=V÷S,从而可以求出水此时的高度,由此解决问题。水箱的底面积是40×30=1200(平方厘米),水的体积是1200×10=12000(立方厘米),铁块的底面积是20×20=400(平方厘米),放入铁块后,水箱的底面积变成了1200-400=800(平方厘米),这时水面高12000÷800=15(厘米)。
解答:这时水面高为15厘米。
有大、中、小三个正方形水池,它们的内边长分别是6米、3米、2米。把两堆碎石分别沉没在中、小水池的水里,两个水池的水面分别升高了6厘米和4厘米。如果将这两堆碎石都沉没在大水池的水里,大水池的水面升高了多少厘米?
【解析】把碎石沉没在水中,水面升高所增加的体积,就等于所沉入碎石的体积。因此,沉入水池中碎石的体积是3×3×0.06=0.54(米?),而沉入小水池中碎石的体积是2×2×0.04=0.16(米?),这两堆碎石的体积一共是0.54+0.16=0.7(米?)。把它们都沉入大水池里,大水池水面升高所增加的体积也就是0.7米3。大水池的底面积是6×6=36(米?)。所以水面升高了0.7÷36=(厘米)。
解答:大水池的水面升高了厘米。
一根长方体木料,体积是0.078立方米。已知这根木料长1.3米,宽为3分米,高该是多少分米?至慧兔把高错算为3分米,那么,这根木料的体积要比0.078立方米多多少?
【解析】0.078÷(1.3×0.3)=0.2(米),0.2米=2分米;
1.3×0.3×0.3-0.078=0.039(立方米)。
解答:这根木料的高是2分米;算错后,这根木料的体积比0.078立方米多0.039立方米。
有一个长方体的盒子,从里面量长40厘米,宽12厘米,高7厘米,在这个盒子里放长5厘米,宽4厘米,高3厘米的长方体木块。最多可放多少块?
【解析】下图表明3×4的长方形可以填满7×12的长方形。于是5×3×4的长方体可以填满40×7×12的长方体,即盒子中最多可放这种长方体40×7×12÷(5×3×4)=56(个)。
长方体的表面积是33.66平方分米,其中一个面的长是2.3分米,宽是2.1分米,它的体积是立方分米?
【解析】长方体的高是(33.66-2.1×2.3×2)÷2÷(2.1+2.3)=(分米)。
解答:长方体的体积是2.1×2.3×=(立方分米)。
约翰·何顿·康威(John Horton Conway,1937年12月26日-),生于英国利物浦,数学家,活跃于有限群的研究、趣味数学、纽结理论、数论、组合博弈论和编码学等范畴。康威年少时就对数学很有强烈的兴趣:四岁时,其母发现他背诵二的次方;十一岁时,升读中学的面试,被问及他成长后想干什么,他回答想在剑桥当数学家。后来康威果然于剑桥大学修读数学,现为普林斯顿大学的教授。
同课章节目录
