六年级上册数学讲义-小升初培优:第07讲 和倍问题 (解析版)全国通用
文档属性
| 名称 | 六年级上册数学讲义-小升初培优:第07讲 和倍问题 (解析版)全国通用 |  | |
| 格式 | doc | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 11:01:34 | ||
图片预览


文档简介
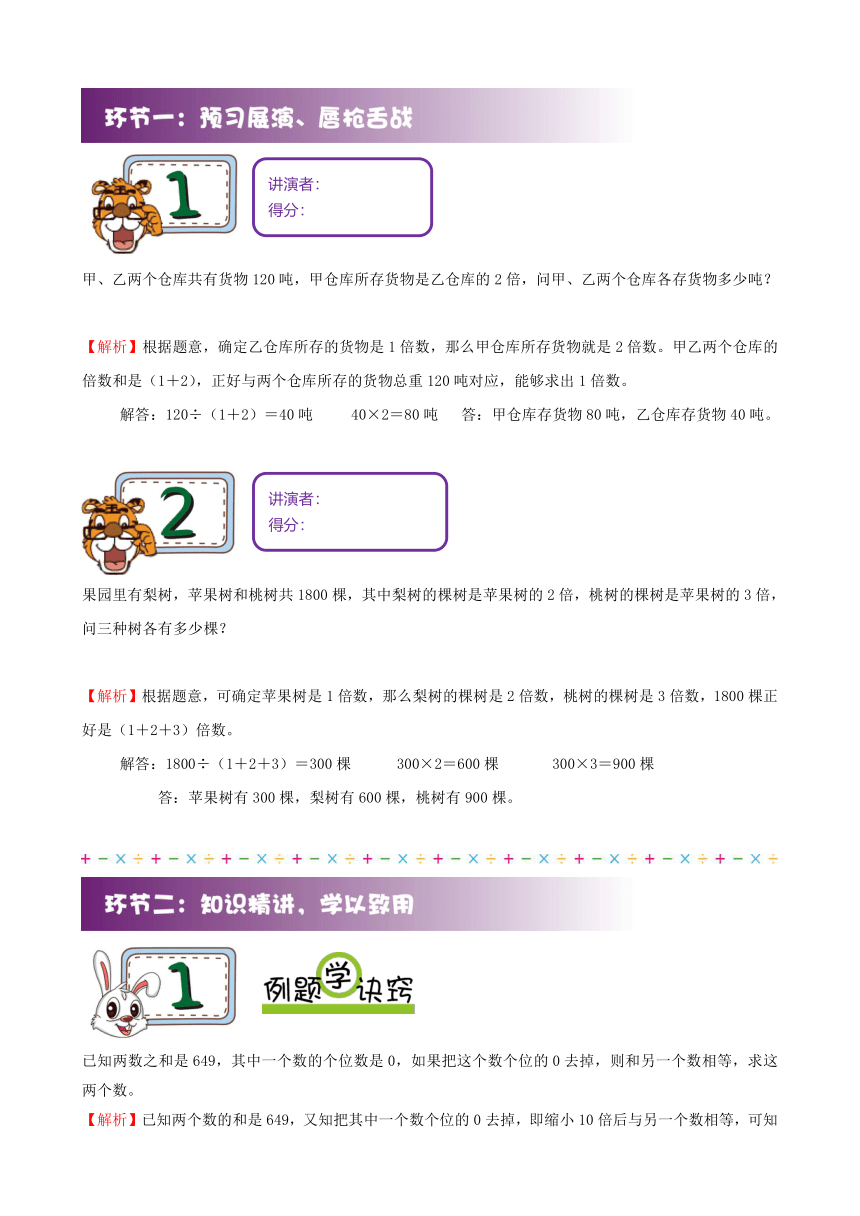
第七讲 和倍问题
甲、乙两个仓库共有货物120吨,甲仓库所存货物是乙仓库的2倍,问甲、乙两个仓库各存货物多少吨?
【解析】根据题意,确定乙仓库所存的货物是1倍数,那么甲仓库所存货物就是2倍数。甲乙两个仓库的倍数和是(1+2),正好与两个仓库所存的货物总重120吨对应,能够求出1倍数。
解答:120÷(1+2)=40吨 40×2=80吨 答:甲仓库存货物80吨,乙仓库存货物40吨。
果园里有梨树,苹果树和桃树共1800棵,其中梨树的棵树是苹果树的2倍,桃树的棵树是苹果树的3倍,问三种树各有多少棵?
【解析】根据题意,可确定苹果树是1倍数,那么梨树的棵树是2倍数,桃树的棵树是3倍数,1800棵正好是(1+2+3)倍数。
解答:1800÷(1+2+3)=300棵 300×2=600棵 300×3=900棵
答:苹果树有300棵,梨树有600棵,桃树有900棵。
已知两数之和是649,其中一个数的个位数是0,如果把这个数个位的0去掉,则和另一个数相等,求这两个数。
【解析】已知两个数的和是649,又知把其中一个数个位的0去掉,即缩小10倍后与另一个数相等,可知大数是小数的10倍,那么两数之和是小数的11倍,则可先求出一倍数,然后再求出另一个数。
解答:小数 649÷(10+1)=649÷11=59 大数 649-59=590或者59×10=590
答:这两个数分别为590和59。
某养鸡场共有鸡、鸭3561只,如果鸡减少60只,鸭增加100只,那么鸡的只数比鸭的只数的2倍还多1只。养鸡场有多少只鸡?多少只鸭?
【解析】画出线段图:鸡减少60只,鸭增加100只后的总数是 3561-60+100=3601(只),如果再减少1只鸡,总数变为3600只,这时鸡的只数正好是鸭的只数的2倍,鸭的只数=3600÷(2+1)=1200(只)。
解答:(3561-60+100-1)÷(2+1)=1200 1200-100=1100 3561-1100=2461
答:养鸡场有2461只鸡,1100只鸭。
水果店运进香蕉、苹果、生梨共846千克,运来的香蕉比苹果的2倍还多17千克,运来的生梨比苹果的3倍少11千克,问运来香蕉多少千克?
【解析】根据题意画出线段图,846千克减去17千克,可得香蕉的重量是苹果的2倍,在(846-17)千克加上11千克,可得生梨的重量是苹果的3倍,则(846-17+11)千克对应的倍数为(1+2+3)倍。
解答:(846-17+11)÷(1+2+3)=140千克 140×2+17=297千克
答:运来香蕉297千克。
把一个减法算式里的被减数、减数与差相加,得数是592,已知减数比差的2倍还大2,问减数是多少?
【解析】已知减数比差的2倍还大2,根据减法的运算关系我们又知:被减数=减数+差,因此被减数必定比差的3倍还大2。根据三者的关系我们画线段图:可以看出592包含了6份差和2个2,由此从592中减去2个2可以得到6份差,可以先求出差,那么减数也就迎刃而解了。
解答: 差 (592-2-2)÷(1+2+3)=98。 减数98×2+2=198。
有货物108件,分成四堆存放在仓库时,第一堆件数的2倍等于第二堆件数的一半,比第三堆的件数少2,比第四堆的件数多2.问每堆各存放多少件?
【解析】第一堆件数的2倍等于第二堆件数的一半,第二堆是第一堆的4倍;比第三堆的件数少2,第三堆是第一堆的2倍多2;比第四堆的件数多2,第四队是第一堆的2倍少2;和倍问题。
解答:第一堆的件数=(108-2+2)÷(1+4+2+2)=12件,第二堆的件数=12×4=48件
第三堆的件数=2×12+2=26件,第四堆的件数=2×12-2=22件。
在悉尼奥运会上,中国队与荷兰队共获金牌40枚,中国队的金牌数比荷兰队的3倍少8枚。中国队、荷兰队各获金牌多少枚?
?
【解析】由条件“中国队的金牌数比荷兰队的3倍少8枚”,可把荷兰队的金牌数看作一份,那么中国队的金牌数为3份减8。如果把中国队与荷兰队的金牌总数40枚再加上8枚,就等于荷兰队金牌数的4倍。
解答:荷兰队的金牌数:(40+8)÷(3+1)=12(枚) 中国队的金牌数:40-12=28(枚)
答:中国队获金牌28枚,荷兰队获金牌12枚。
小明、小红、小玲共有73块糖。如果小玲吃掉3块,那么小红与小玲的糖就一样多;如果小红给小明2块糖,那么小明的糖就是小红的糖的2倍。问小红有多少块糖?
【解析】如果小玲吃掉3块,那么小红与小玲的糖就一样多,说明小玲比小红多3块;如果小红给小明2块糖,那么小明的糖就是小红的糖的2倍,即小明加2是小红减2后的2倍,说明小明是小红的2倍少6(2×2+2)。这是一个和倍问题。
??解答:小红的颗数=(73-3+6)÷(1+1+2)=19块。
在书架上摆放着三层书共275本,第三层的书比第二层的3倍多8 本,第一层比第二层的2倍少3本。第三层上摆放着多少本书?
【解析】 画线段图根据线段图一层为少3本,三层为多8本,多去少补。
解答:(275-3+8)÷(2+1+3)=45(本) 45×3+8=143(本)
答:第三层上摆放着143本书。
欧拉的故事
欧拉是数学史上著名的数学家,他在数论、几何学、天文数学、微积分等好几个数学的分支领域中都取得了出色的成就。不过,这个大数学家在孩提时代却一点也不讨老师的喜欢,他是一个被学校除了名的小学生。
回家后无事的他就帮助爸爸放羊,成了一个牧童。他一面放羊,一面读书。他读的书中,有不少数学书。爸爸的羊群渐渐增多了,达到了100只。原来的羊圈有点小了,爸爸决定建造一个新的羊圈。他用尺量出了一块长方形的土地,长40米,宽15米,他一算,面积正好是600平方米,平均每一头羊占地6平方米。正打算动工的时候,他发现他的材料只够围100米的篱笆,不够用。若要围成长40米,宽15米的羊圈,其周长将是110米(15+15+40+40=110)。父亲感到很为难,若要按原计划建造,就要再添10米长的材料;要是缩小面积,每头羊的面积就会小于6平方米。小欧拉却向父亲说,不用缩小羊圈,也不用担心每头羊的领地会小于原来的计划。父亲不相信小欧拉会有办法,听了没有理他。小欧拉急了,大声说,只有稍稍移动一下羊圈的桩子就行了。父亲听了直摇头,心想:"世界上哪有这样便宜的事情?"但是,小欧拉却坚持说,他一定能两全齐美,父亲终于同意让儿子试试看。小欧拉见父亲同意了,站起身来,跑到准备动工的羊圈旁。他以一个木桩为中心,将原来的40米边长截短,缩短到25米。父亲着急了,说:"那怎么成呢?那怎么成呢?这个羊圈太小了,太小了。"小欧拉也不回答,跑到另一条边上,将原来15米的边长延长,又增加了10米,变成了25米。经这样一改,原来计划中的羊圈变成了一个25米边长的正方形。然后,小欧拉很自信地对爸爸说:"现在,篱笆也够了,面积也够了。"父亲照着小欧拉设计的羊圈扎上了篱笆,100米长的篱笆真的够了,不多不少,全部用光。面积也足够了,而且还稍稍大了一些。父亲心里感到非常高兴。孩子比自己聪明,真会动脑筋,将来一定大有出息。
父亲感到,让这么聪明的孩子放羊实在是可惜了。后来,他想办法让小欧拉认识了一个大数学家伯努利。通过这位数学家的推荐,1720年,小欧拉成了巴塞尔大学的大学生。这一年,小欧拉13岁,是这所大学最年轻的大学生
甲、乙两个仓库共有货物120吨,甲仓库所存货物是乙仓库的2倍,问甲、乙两个仓库各存货物多少吨?
【解析】根据题意,确定乙仓库所存的货物是1倍数,那么甲仓库所存货物就是2倍数。甲乙两个仓库的倍数和是(1+2),正好与两个仓库所存的货物总重120吨对应,能够求出1倍数。
解答:120÷(1+2)=40吨 40×2=80吨 答:甲仓库存货物80吨,乙仓库存货物40吨。
果园里有梨树,苹果树和桃树共1800棵,其中梨树的棵树是苹果树的2倍,桃树的棵树是苹果树的3倍,问三种树各有多少棵?
【解析】根据题意,可确定苹果树是1倍数,那么梨树的棵树是2倍数,桃树的棵树是3倍数,1800棵正好是(1+2+3)倍数。
解答:1800÷(1+2+3)=300棵 300×2=600棵 300×3=900棵
答:苹果树有300棵,梨树有600棵,桃树有900棵。
已知两数之和是649,其中一个数的个位数是0,如果把这个数个位的0去掉,则和另一个数相等,求这两个数。
【解析】已知两个数的和是649,又知把其中一个数个位的0去掉,即缩小10倍后与另一个数相等,可知大数是小数的10倍,那么两数之和是小数的11倍,则可先求出一倍数,然后再求出另一个数。
解答:小数 649÷(10+1)=649÷11=59 大数 649-59=590或者59×10=590
答:这两个数分别为590和59。
某养鸡场共有鸡、鸭3561只,如果鸡减少60只,鸭增加100只,那么鸡的只数比鸭的只数的2倍还多1只。养鸡场有多少只鸡?多少只鸭?
【解析】画出线段图:鸡减少60只,鸭增加100只后的总数是 3561-60+100=3601(只),如果再减少1只鸡,总数变为3600只,这时鸡的只数正好是鸭的只数的2倍,鸭的只数=3600÷(2+1)=1200(只)。
解答:(3561-60+100-1)÷(2+1)=1200 1200-100=1100 3561-1100=2461
答:养鸡场有2461只鸡,1100只鸭。
水果店运进香蕉、苹果、生梨共846千克,运来的香蕉比苹果的2倍还多17千克,运来的生梨比苹果的3倍少11千克,问运来香蕉多少千克?
【解析】根据题意画出线段图,846千克减去17千克,可得香蕉的重量是苹果的2倍,在(846-17)千克加上11千克,可得生梨的重量是苹果的3倍,则(846-17+11)千克对应的倍数为(1+2+3)倍。
解答:(846-17+11)÷(1+2+3)=140千克 140×2+17=297千克
答:运来香蕉297千克。
把一个减法算式里的被减数、减数与差相加,得数是592,已知减数比差的2倍还大2,问减数是多少?
【解析】已知减数比差的2倍还大2,根据减法的运算关系我们又知:被减数=减数+差,因此被减数必定比差的3倍还大2。根据三者的关系我们画线段图:可以看出592包含了6份差和2个2,由此从592中减去2个2可以得到6份差,可以先求出差,那么减数也就迎刃而解了。
解答: 差 (592-2-2)÷(1+2+3)=98。 减数98×2+2=198。
有货物108件,分成四堆存放在仓库时,第一堆件数的2倍等于第二堆件数的一半,比第三堆的件数少2,比第四堆的件数多2.问每堆各存放多少件?
【解析】第一堆件数的2倍等于第二堆件数的一半,第二堆是第一堆的4倍;比第三堆的件数少2,第三堆是第一堆的2倍多2;比第四堆的件数多2,第四队是第一堆的2倍少2;和倍问题。
解答:第一堆的件数=(108-2+2)÷(1+4+2+2)=12件,第二堆的件数=12×4=48件
第三堆的件数=2×12+2=26件,第四堆的件数=2×12-2=22件。
在悉尼奥运会上,中国队与荷兰队共获金牌40枚,中国队的金牌数比荷兰队的3倍少8枚。中国队、荷兰队各获金牌多少枚?
?
【解析】由条件“中国队的金牌数比荷兰队的3倍少8枚”,可把荷兰队的金牌数看作一份,那么中国队的金牌数为3份减8。如果把中国队与荷兰队的金牌总数40枚再加上8枚,就等于荷兰队金牌数的4倍。
解答:荷兰队的金牌数:(40+8)÷(3+1)=12(枚) 中国队的金牌数:40-12=28(枚)
答:中国队获金牌28枚,荷兰队获金牌12枚。
小明、小红、小玲共有73块糖。如果小玲吃掉3块,那么小红与小玲的糖就一样多;如果小红给小明2块糖,那么小明的糖就是小红的糖的2倍。问小红有多少块糖?
【解析】如果小玲吃掉3块,那么小红与小玲的糖就一样多,说明小玲比小红多3块;如果小红给小明2块糖,那么小明的糖就是小红的糖的2倍,即小明加2是小红减2后的2倍,说明小明是小红的2倍少6(2×2+2)。这是一个和倍问题。
??解答:小红的颗数=(73-3+6)÷(1+1+2)=19块。
在书架上摆放着三层书共275本,第三层的书比第二层的3倍多8 本,第一层比第二层的2倍少3本。第三层上摆放着多少本书?
【解析】 画线段图根据线段图一层为少3本,三层为多8本,多去少补。
解答:(275-3+8)÷(2+1+3)=45(本) 45×3+8=143(本)
答:第三层上摆放着143本书。
欧拉的故事
欧拉是数学史上著名的数学家,他在数论、几何学、天文数学、微积分等好几个数学的分支领域中都取得了出色的成就。不过,这个大数学家在孩提时代却一点也不讨老师的喜欢,他是一个被学校除了名的小学生。
回家后无事的他就帮助爸爸放羊,成了一个牧童。他一面放羊,一面读书。他读的书中,有不少数学书。爸爸的羊群渐渐增多了,达到了100只。原来的羊圈有点小了,爸爸决定建造一个新的羊圈。他用尺量出了一块长方形的土地,长40米,宽15米,他一算,面积正好是600平方米,平均每一头羊占地6平方米。正打算动工的时候,他发现他的材料只够围100米的篱笆,不够用。若要围成长40米,宽15米的羊圈,其周长将是110米(15+15+40+40=110)。父亲感到很为难,若要按原计划建造,就要再添10米长的材料;要是缩小面积,每头羊的面积就会小于6平方米。小欧拉却向父亲说,不用缩小羊圈,也不用担心每头羊的领地会小于原来的计划。父亲不相信小欧拉会有办法,听了没有理他。小欧拉急了,大声说,只有稍稍移动一下羊圈的桩子就行了。父亲听了直摇头,心想:"世界上哪有这样便宜的事情?"但是,小欧拉却坚持说,他一定能两全齐美,父亲终于同意让儿子试试看。小欧拉见父亲同意了,站起身来,跑到准备动工的羊圈旁。他以一个木桩为中心,将原来的40米边长截短,缩短到25米。父亲着急了,说:"那怎么成呢?那怎么成呢?这个羊圈太小了,太小了。"小欧拉也不回答,跑到另一条边上,将原来15米的边长延长,又增加了10米,变成了25米。经这样一改,原来计划中的羊圈变成了一个25米边长的正方形。然后,小欧拉很自信地对爸爸说:"现在,篱笆也够了,面积也够了。"父亲照着小欧拉设计的羊圈扎上了篱笆,100米长的篱笆真的够了,不多不少,全部用光。面积也足够了,而且还稍稍大了一些。父亲心里感到非常高兴。孩子比自己聪明,真会动脑筋,将来一定大有出息。
父亲感到,让这么聪明的孩子放羊实在是可惜了。后来,他想办法让小欧拉认识了一个大数学家伯努利。通过这位数学家的推荐,1720年,小欧拉成了巴塞尔大学的大学生。这一年,小欧拉13岁,是这所大学最年轻的大学生
同课章节目录
