六年级上册数学讲义-小升初培优:第07讲 图形面积(解析版)全国通用
文档属性
| 名称 | 六年级上册数学讲义-小升初培优:第07讲 图形面积(解析版)全国通用 |
|
|
| 格式 | doc | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 00:00:00 | ||
图片预览

文档简介
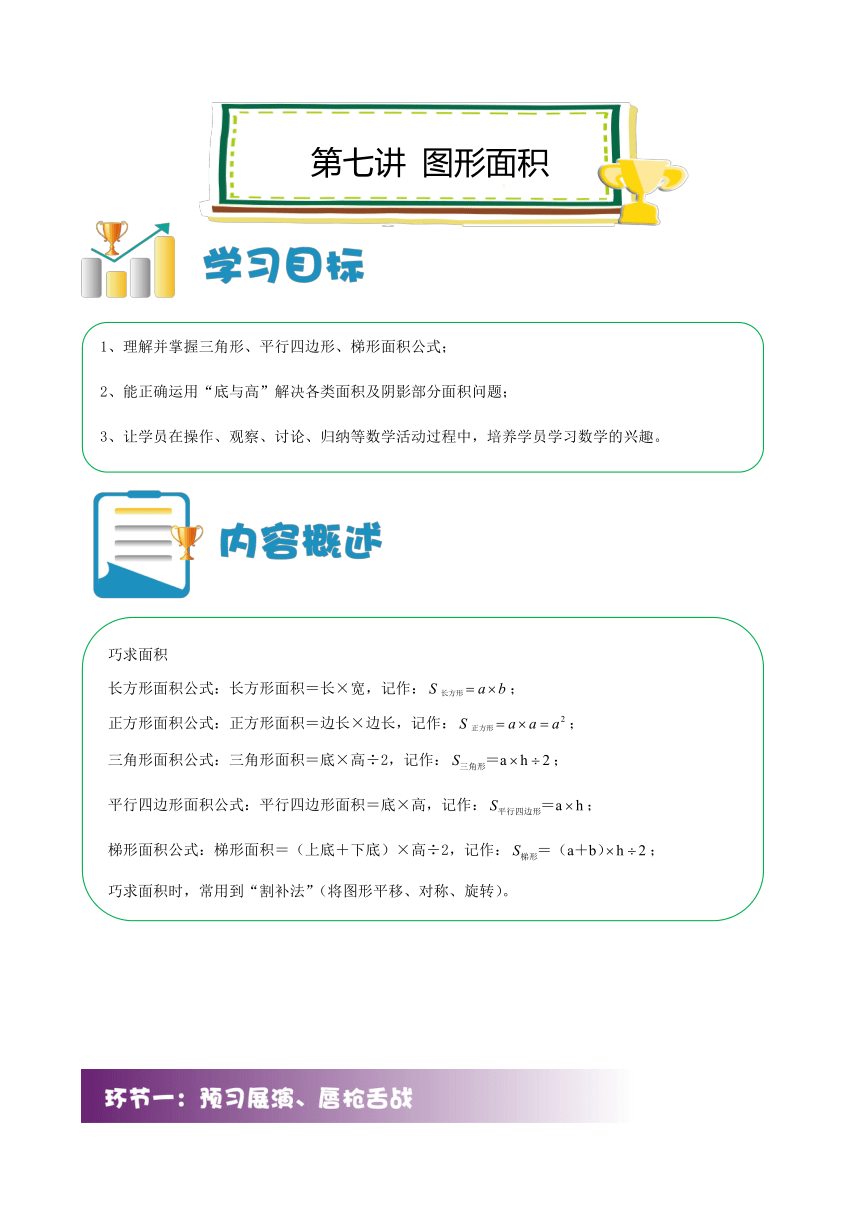
第七讲 图形面积
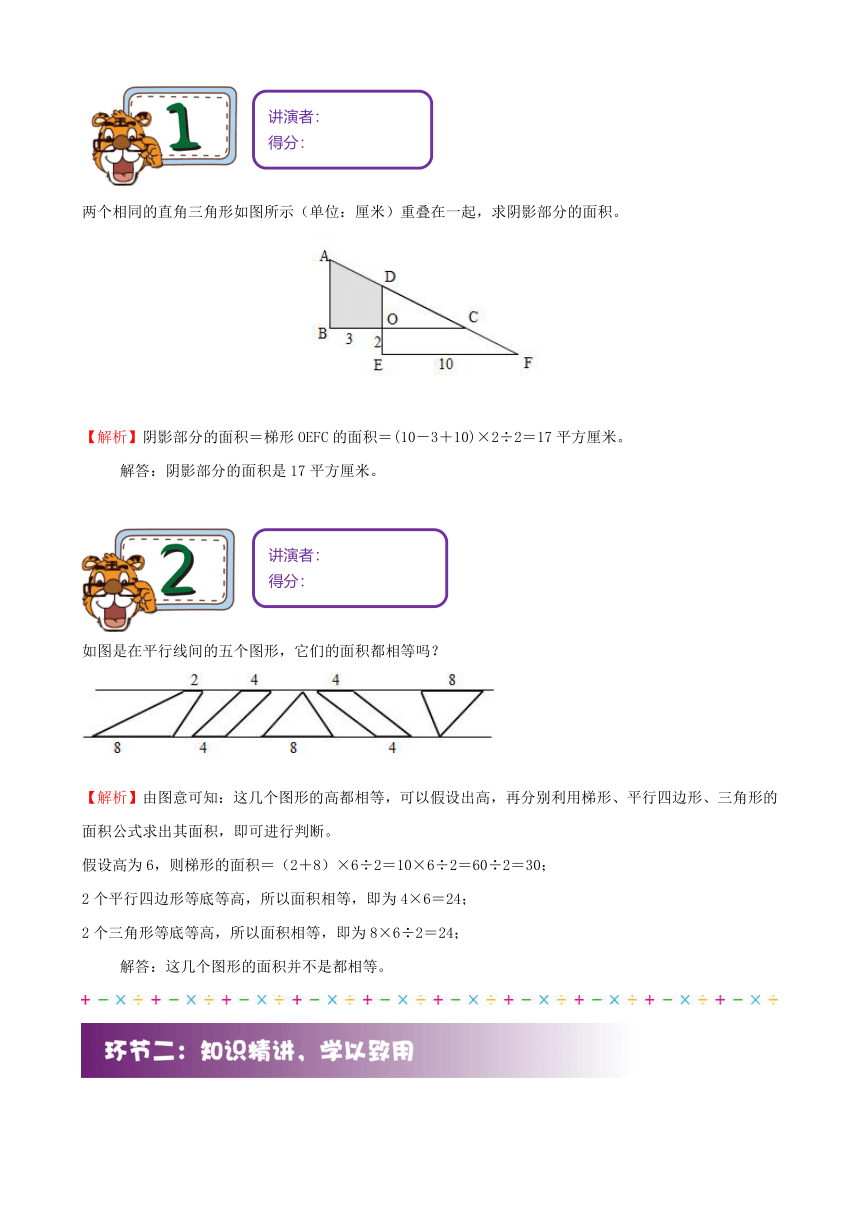
两个相同的直角三角形如图所示(单位:厘米)重叠在一起,求阴影部分的面积。
【解析】阴影部分的面积=梯形OEFC的面积=(10-3+10)×2÷2=17平方厘米。
解答:阴影部分的面积是17平方厘米。
如图是在平行线间的五个图形,它们的面积都相等吗?
【解析】由图意可知:这几个图形的高都相等,可以假设出高,再分别利用梯形、平行四边形、三角形的面积公式求出其面积,即可进行判断。
假设高为6,则梯形的面积=(2+8)×6÷2=10×6÷2=60÷2=30;
2个平行四边形等底等高,所以面积相等,即为4×6=24;
2个三角形等底等高,所以面积相等,即为8×6÷2=24;
解答:这几个图形的面积并不是都相等。
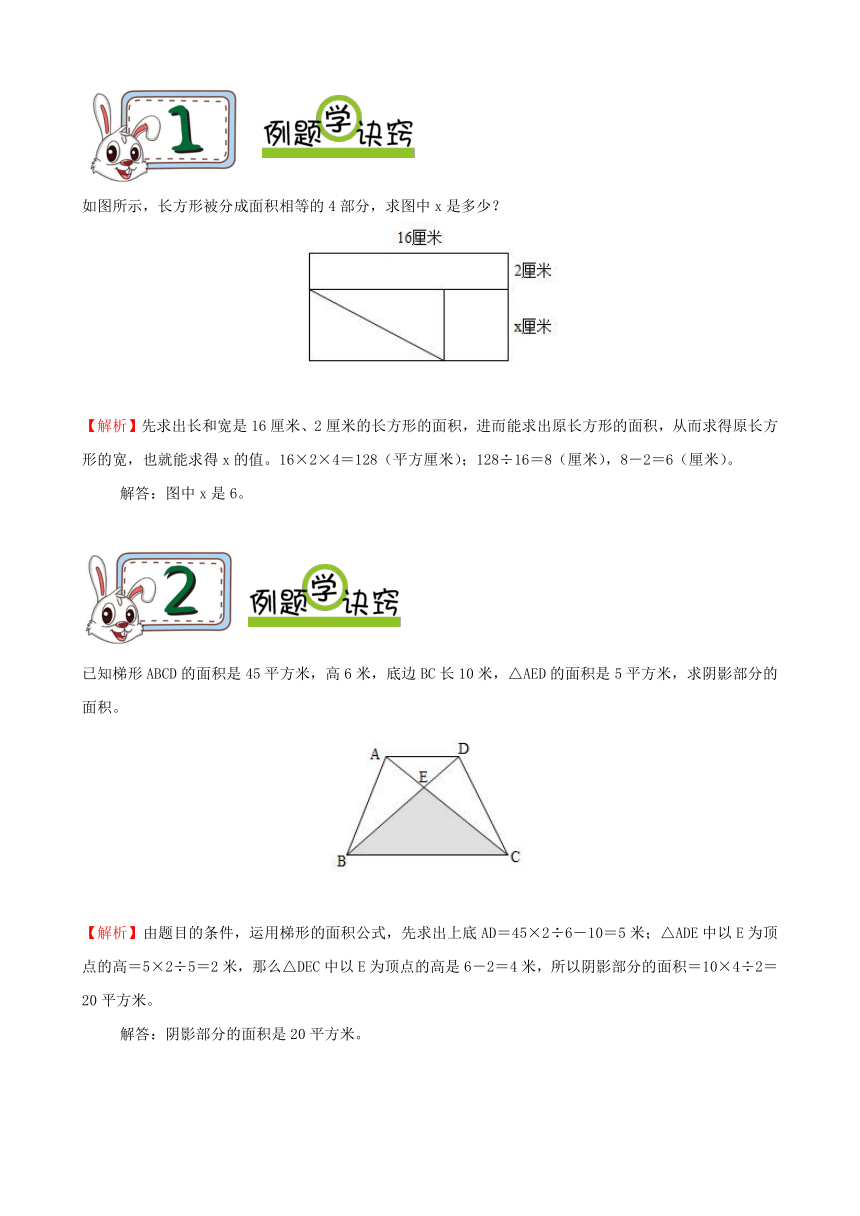
如图所示,长方形被分成面积相等的4部分,求图中x是多少?
【解析】先求出长和宽是16厘米、2厘米的长方形的面积,进而能求出原长方形的面积,从而求得原长方形的宽,也就能求得x的值。16×2×4=128(平方厘米);128÷16=8(厘米),8-2=6(厘米)。
解答:图中x是6。
已知梯形ABCD的面积是45平方米,高6米,底边BC长10米,△AED的面积是5平方米,求阴影部分的面积。
【解析】由题目的条件,运用梯形的面积公式,先求出上底AD=45×2÷6-10=5米;△ADE中以E为顶点的高=5×2÷5=2米,那么△DEC中以E为顶点的高是6-2=4米,所以阴影部分的面积=10×4÷2=20平方米。
解答:阴影部分的面积是20平方米。
大正方形的面积为9平方厘米,中间小正方形的面积为1平方厘米,甲、乙、丙、丁是四个梯形。那么乙和丁的面积之和是多少平方厘米?
【解析】所有的梯形上下底之和相同,而甲和丙,乙和丁高之和是相同的,所以甲丙面积和等于乙丁的面积和。(9-1)÷2=4平方厘米。
解答:乙和丁的面积之和是4平方厘米。
如图所示,ABCD是梯形,三角形ADE的面积为1,三角形ABF的面积为9,三角形BCF的面积为27,则三角形ACE的面积为多少?
【解析】(1)三角形ABF的面积为9,三角形BCF的面积为27,根据高一定时,三角形的面积与底成正比例的性质可得:AF:FC=9:27=1:3,梯形ABCD中,三角形ADF与三角形BFC相似,相似比是AF:FC=1:3,则它们的面积之比等于相似比的平方:1:9,所以三角形ADF的面积是:27÷9=3;
(2)又因为三角形ADE的面积是1,所以三角形AEF的面积是2,根据高一定时,三角形的面积与底成正比例的性质,再求出三角形EFC的面积即可解决问题。
解答:三角形AEC的面积是8。
已知平行四边形ABCD的面积是100平方厘米,△ABE的面积是31平方厘米,求△BEF的面积。
【解析】连接AC,△ABF的面积=△ABC的面积=100÷2=50平方厘米,△BEF的面积:50-31=19平方厘米。
解答:△BEF的面积是19平方厘米。
在下图直角梯形中,AB=8厘米,CD=4厘米,BC=6厘米,△AFB比△EFD 的面积大18平方厘米。求ED长。
【解析】梯形ABCD的面积:(8+4)×6÷2=36;△BCE 的面积:36-18=18;CE长:18×2÷6=6;ED长:6-4=2厘米
解答:ED长2厘米。
如下图,梯形ABCD中,下底是上底长的2倍,E是AB的中点,那么梯形ABCD面积是△BDE面积的几倍?
【解析】△ADE面积=△BDE面积=△BDC面积;
解答:梯形ABCD面积是△BDE面积的3倍。
如下图,梯形内有两个三角形,面积分别为6平方厘米和8平方厘米,且下底是上底的2倍,阴影部分的面积是多少平方厘米?
【解析】取下底中点M,△OCM的面积=8÷2=4平方厘米,BM=CM=AD
∵△OAD的面积=6平方厘米∴OE=1.5 OF
设OF=h,梯形的高为2.5h,且ah=8平方厘米,(a+2a)×2.5h÷2=7.5ah÷2=30平方厘米,
阴影部分的面积=30-6-8=16平方厘米。
解答:阴影部分的面积是16平方厘米。
中国古代数学著作—《九章重差图》
_??????_: 《海岛算经》 《_??????????????¨_》 《九章重差图》。
263年左右,刘徽发现当圆内接_????¤?è?????_的边数无限增加时,多边形的面积则可无限逼近_???é???§?_,即所谓“割之弥细,所失弥少,割之又割,以至于不可割,则与_?????¨_合体而无所失矣。”刘徽采用了以直代曲、无限趋近、“内外夹逼”的思想,创立了“_?????????_”。
《重差》原为《九章算术注》的第十卷,即后来的《海岛算经》,内容是测量目标物的高和远的计算方法,重差法是测量数学中的重要方法。
_?????????_:(公元429年─公元500年)是我国杰出的数学家、科学家,南北朝时期汉族人,字文远。他当时就把_?????¨_率精确到小数点后7位(3.1415926<圆周率<3.1415927),比西方领先了1500年,并得出的_??????_和的_??????_。《缀术》记载了他计算圆周率的方法,不过已经失传。
两个相同的直角三角形如图所示(单位:厘米)重叠在一起,求阴影部分的面积。
【解析】阴影部分的面积=梯形OEFC的面积=(10-3+10)×2÷2=17平方厘米。
解答:阴影部分的面积是17平方厘米。
如图是在平行线间的五个图形,它们的面积都相等吗?
【解析】由图意可知:这几个图形的高都相等,可以假设出高,再分别利用梯形、平行四边形、三角形的面积公式求出其面积,即可进行判断。
假设高为6,则梯形的面积=(2+8)×6÷2=10×6÷2=60÷2=30;
2个平行四边形等底等高,所以面积相等,即为4×6=24;
2个三角形等底等高,所以面积相等,即为8×6÷2=24;
解答:这几个图形的面积并不是都相等。
如图所示,长方形被分成面积相等的4部分,求图中x是多少?
【解析】先求出长和宽是16厘米、2厘米的长方形的面积,进而能求出原长方形的面积,从而求得原长方形的宽,也就能求得x的值。16×2×4=128(平方厘米);128÷16=8(厘米),8-2=6(厘米)。
解答:图中x是6。
已知梯形ABCD的面积是45平方米,高6米,底边BC长10米,△AED的面积是5平方米,求阴影部分的面积。
【解析】由题目的条件,运用梯形的面积公式,先求出上底AD=45×2÷6-10=5米;△ADE中以E为顶点的高=5×2÷5=2米,那么△DEC中以E为顶点的高是6-2=4米,所以阴影部分的面积=10×4÷2=20平方米。
解答:阴影部分的面积是20平方米。
大正方形的面积为9平方厘米,中间小正方形的面积为1平方厘米,甲、乙、丙、丁是四个梯形。那么乙和丁的面积之和是多少平方厘米?
【解析】所有的梯形上下底之和相同,而甲和丙,乙和丁高之和是相同的,所以甲丙面积和等于乙丁的面积和。(9-1)÷2=4平方厘米。
解答:乙和丁的面积之和是4平方厘米。
如图所示,ABCD是梯形,三角形ADE的面积为1,三角形ABF的面积为9,三角形BCF的面积为27,则三角形ACE的面积为多少?
【解析】(1)三角形ABF的面积为9,三角形BCF的面积为27,根据高一定时,三角形的面积与底成正比例的性质可得:AF:FC=9:27=1:3,梯形ABCD中,三角形ADF与三角形BFC相似,相似比是AF:FC=1:3,则它们的面积之比等于相似比的平方:1:9,所以三角形ADF的面积是:27÷9=3;
(2)又因为三角形ADE的面积是1,所以三角形AEF的面积是2,根据高一定时,三角形的面积与底成正比例的性质,再求出三角形EFC的面积即可解决问题。
解答:三角形AEC的面积是8。
已知平行四边形ABCD的面积是100平方厘米,△ABE的面积是31平方厘米,求△BEF的面积。
【解析】连接AC,△ABF的面积=△ABC的面积=100÷2=50平方厘米,△BEF的面积:50-31=19平方厘米。
解答:△BEF的面积是19平方厘米。
在下图直角梯形中,AB=8厘米,CD=4厘米,BC=6厘米,△AFB比△EFD 的面积大18平方厘米。求ED长。
【解析】梯形ABCD的面积:(8+4)×6÷2=36;△BCE 的面积:36-18=18;CE长:18×2÷6=6;ED长:6-4=2厘米
解答:ED长2厘米。
如下图,梯形ABCD中,下底是上底长的2倍,E是AB的中点,那么梯形ABCD面积是△BDE面积的几倍?
【解析】△ADE面积=△BDE面积=△BDC面积;
解答:梯形ABCD面积是△BDE面积的3倍。
如下图,梯形内有两个三角形,面积分别为6平方厘米和8平方厘米,且下底是上底的2倍,阴影部分的面积是多少平方厘米?
【解析】取下底中点M,△OCM的面积=8÷2=4平方厘米,BM=CM=AD
∵△OAD的面积=6平方厘米∴OE=1.5 OF
设OF=h,梯形的高为2.5h,且ah=8平方厘米,(a+2a)×2.5h÷2=7.5ah÷2=30平方厘米,
阴影部分的面积=30-6-8=16平方厘米。
解答:阴影部分的面积是16平方厘米。
中国古代数学著作—《九章重差图》
_??????_: 《海岛算经》 《_??????????????¨_》 《九章重差图》。
263年左右,刘徽发现当圆内接_????¤?è?????_的边数无限增加时,多边形的面积则可无限逼近_???é???§?_,即所谓“割之弥细,所失弥少,割之又割,以至于不可割,则与_?????¨_合体而无所失矣。”刘徽采用了以直代曲、无限趋近、“内外夹逼”的思想,创立了“_?????????_”。
《重差》原为《九章算术注》的第十卷,即后来的《海岛算经》,内容是测量目标物的高和远的计算方法,重差法是测量数学中的重要方法。
_?????????_:(公元429年─公元500年)是我国杰出的数学家、科学家,南北朝时期汉族人,字文远。他当时就把_?????¨_率精确到小数点后7位(3.1415926<圆周率<3.1415927),比西方领先了1500年,并得出的_??????_和的_??????_。《缀术》记载了他计算圆周率的方法,不过已经失传。
同课章节目录
