六年级上册数学讲义-小升初培优:第08讲 等积变形(解析版)全国通用
文档属性
| 名称 | 六年级上册数学讲义-小升初培优:第08讲 等积变形(解析版)全国通用 |  | |
| 格式 | doc | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 07:48:44 | ||
图片预览

文档简介
第八讲 等积变形
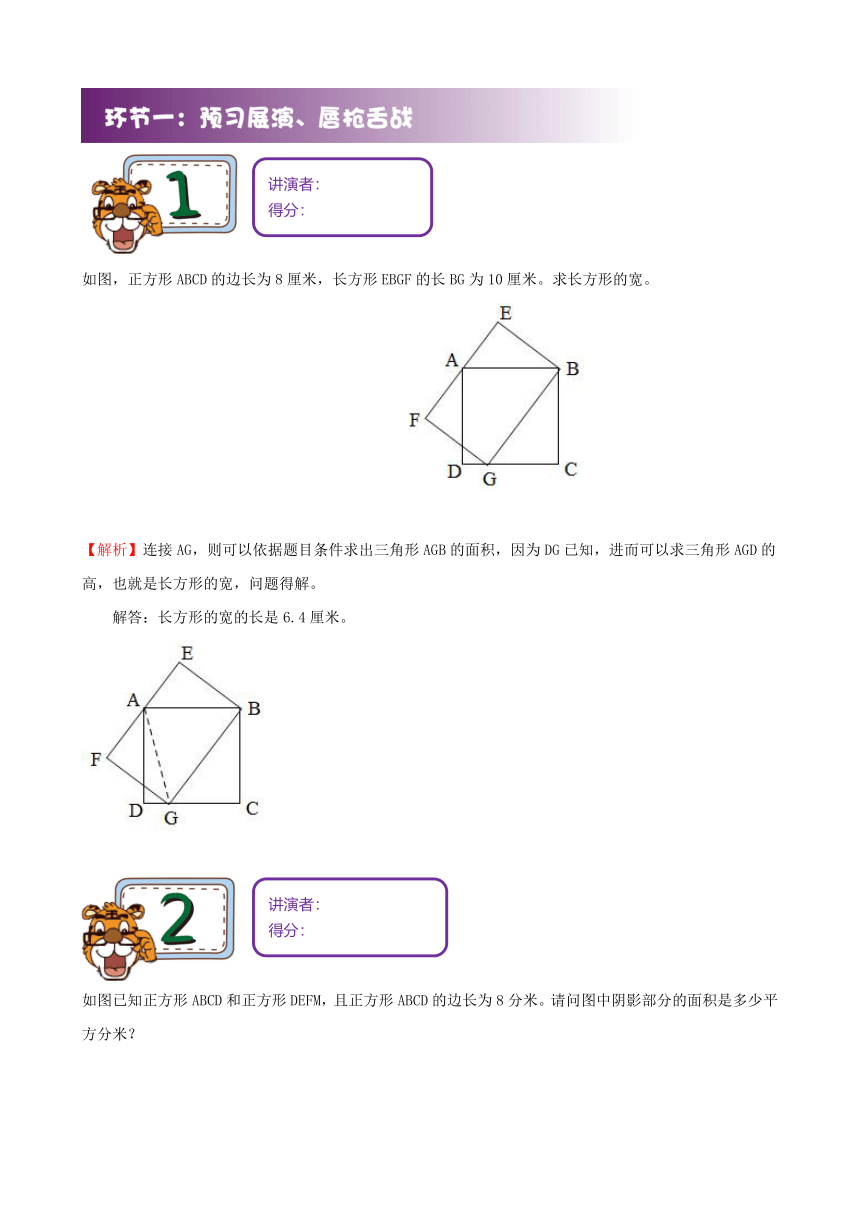
如图,正方形ABCD的边长为8厘米,长方形EBGF的长BG为10厘米。求长方形的宽。
【解析】连接AG,则可以依据题目条件求出三角形AGB的面积,因为DG已知,进而可以求三角形AGD的高,也就是长方形的宽,问题得解。
解答:长方形的宽的长是6.4厘米。
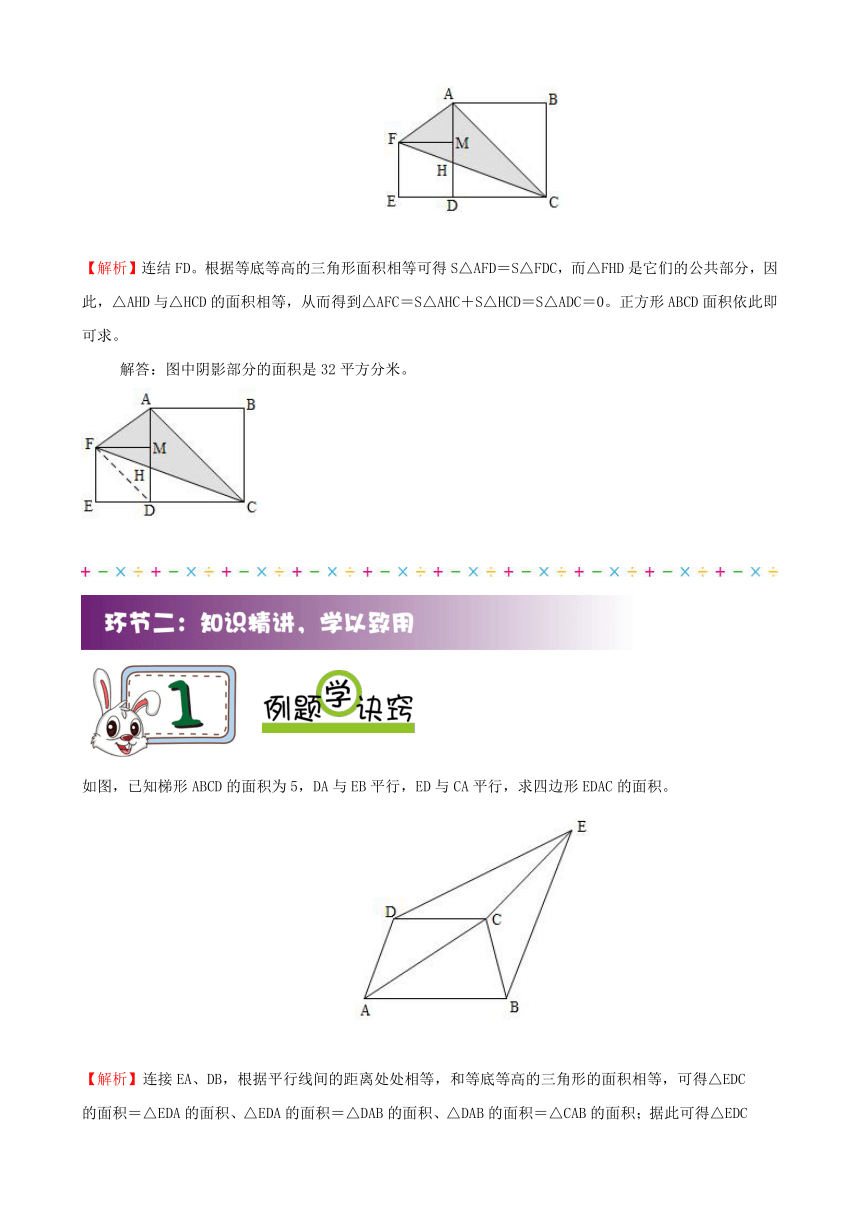
如图已知正方形ABCD和正方形DEFM,且正方形ABCD的边长为8分米。请问图中阴影部分的面积是多少平方分米?
【解析】连结FD。根据等底等高的三角形面积相等可得S△AFD=S△FDC,而△FHD是它们的公共部分,因此,△AHD与△HCD的面积相等,从而得到△AFC=S△AHC+S△HCD=S△ADC=0。正方形ABCD面积依此即可求。
解答:图中阴影部分的面积是32平方分米。
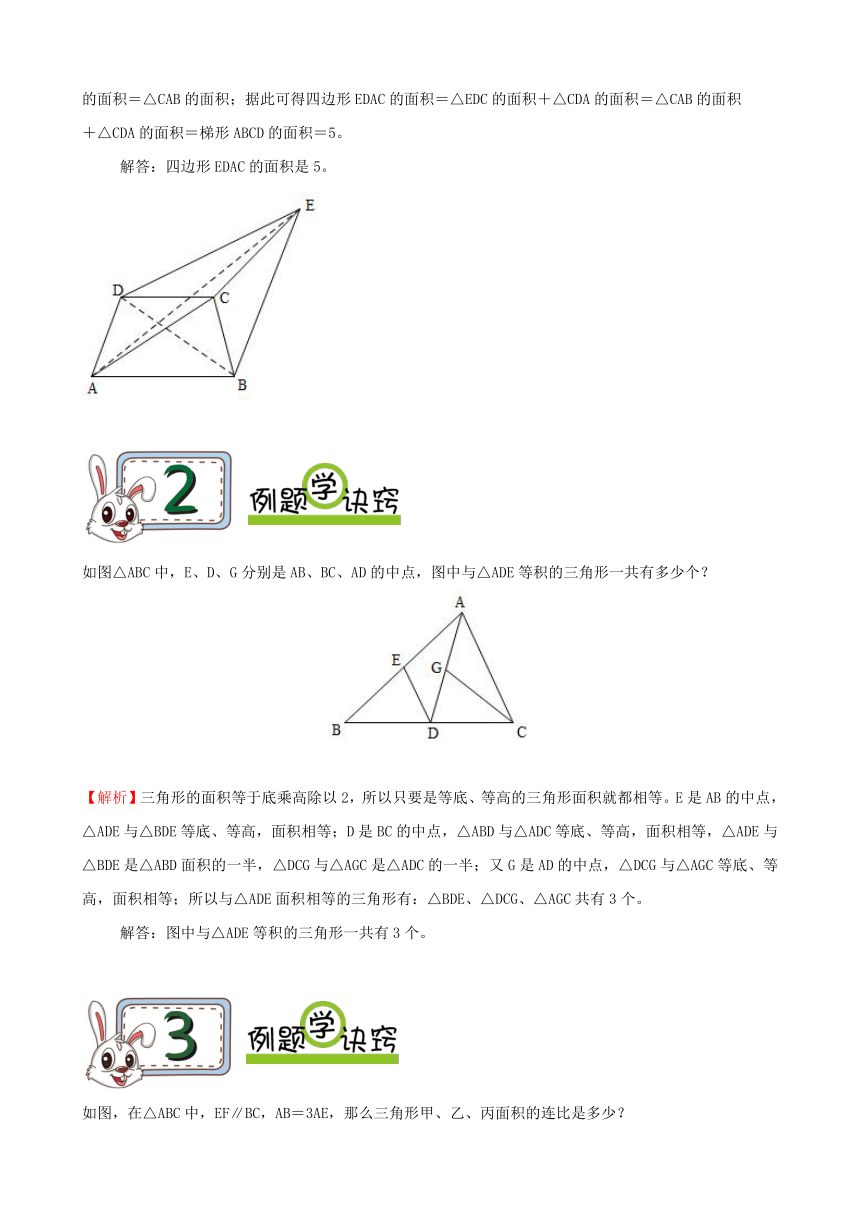
如图,已知梯形ABCD的面积为5,DA与EB平行,ED与CA平行,求四边形EDAC的面积。
【解析】连接EA、DB,根据平行线间的距离处处相等,和等底等高的三角形的面积相等,可得△EDC的面积=△EDA的面积、△EDA的面积=△DAB的面积、△DAB的面积=△CAB的面积;据此可得△EDC的面积=△CAB的面积;据此可得四边形EDAC的面积=△EDC的面积+△CDA的面积=△CAB的面积+△CDA的面积=梯形ABCD的面积=5。
解答:四边形EDAC的面积是5。
如图△ABC中,E、D、G分别是AB、BC、AD的中点,图中与△ADE等积的三角形一共有多少个?
【解析】三角形的面积等于底乘高除以2,所以只要是等底、等高的三角形面积就都相等。E是AB的中点,△ADE与△BDE等底、等高,面积相等;D是BC的中点,△ABD与△ADC等底、等高,面积相等,△ADE与△BDE是△ABD面积的一半,△DCG与△AGC是△ADC的一半;又G是AD的中点,△DCG与△AGC等底、等高,面积相等;所以与△ADE面积相等的三角形有:△BDE、△DCG、△AGC共有3个。
解答:图中与△ADE等积的三角形一共有3个。
如图,在△ABC中,EF∥BC,AB=3AE,那么三角形甲、乙、丙面积的连比是多少?
【解析】先比较甲和乙的面积,再比较(甲+乙)和丙的面积。
解答:甲、乙、丙面积的连比是1:2:6。
在图中,△ABC的面积是52,AC=13,△FDC是等腰直角三角形,又△ADC与△ABD面积相等,求△ADF的面积是多少?
【解析】△ABC若以BC为底,△ABD以BD为底,△ACD以CD为底,则它们的高相等,△ADC与△ABD面积相等都是26,根据三角形的面积公式可知它们的底也相等,即BD=CD;△ADC以AC为底,那么DF就是AC边上的高,根据它的面积和AC的长度就可以求出DF的长度,进而可求AF的长度,再根据直角三角形的面积公式就可以求出△ADF的面积。
因为S△ABC=52,所以S△ADC=S△ABD=52÷2=26;又因为AC=13,△FDC是等腰直角三角形,所以DF=S△ADC×2÷AC=26×2÷13=4;
因为CF=DF,即CF=4,所以AF=AC-CF=13-4=9;S△ADF=4×9÷2=18。
解答:△ADF的面积是18。
如图,在平行四边形ABCD中,E为BC的中点,DF=2BF,三角形BEF(图中阴影部分)的面积是8平方厘米。求:平行四边形的面积。
【解析】边接CF,△BFE与△CEF的高相同,面积的比就是底的比,E为BC的中点。所以它们面积的比为1:1,△CEF的面积为就是8平方厘米,△BCF与△CDF的高相同,它们面积的比就是底的比,因DF=2BF,所以它们面积的比是2:1,△CDF的面积是32平方厘米,平行四边形ABCD的面积等于三角形BCD的面积2倍。据此可求出平行四边形的面积。
解答:平行四边形的面积是96平方厘米。
长方形ABCD的对角线AC、BD相交于点O,过点O的直线分别交AD、BC于点E、F, AB=2厘米,BC=3厘米,问图中阴影部分的面积是多少平方厘米?
【解析】阴影部分的面积等于空白部分的面积。
解答:阴影部分的面积是3平方厘米。
如图,边长为7的正方形ABCD和边长为5的正方形CEFG并排放在一起,O1和O2分别是两个正方形的中心(正方形对角线的交点),问阴影部分的面积是多少?
【解析】连接CO1 ,CO2 ,我们发现CO2 和O1B平行,那么△O1O2 B和△O1CB的面积相等,所以△BO2 P和△O1PC的面积相等。
解答:阴影部分的面积=7×(7÷2)÷2=12.25。
如图,四边形EFGH的面积是66平方米,EA=AB,CB=BF,DC=CG,HD=DA。求四边形ABCD的面积。
【解析】根据四边形ABCD的面积是66平方米,要求四边形ABCD的面积,只要求出四边形ABCD与四周多出来的四个三角形的面积的关系以及四边形ABCD与四边形EFGH的面积关系,即可解决问题。
连接CA、AF、HC,则三角形ADC的面积=三角形HDC的面积=三角形HCG的面积=三角形HDG的面积的一半,同理可得,ABCD的面积为13.2平方米。
解答:四边形ABCD的面积为13.2平方米。
数学名言(一)
数统治着宇宙。 ——毕达哥拉斯
数学,科学的女皇;数论,数学的女皇。 ——高斯
上帝创造了整数,所有其余的数都是人造的。 ——克隆内克
上帝是一位算术家。 ——雅克比
一个没有几分诗人气的数学家永远成不了一个完全的数学家。——维尔斯特拉斯
纯数学这门科学在其现代发展阶段,可以说是人类精神之最具独创性的创造。——怀德海
整数的简单构成,若干世纪以来一直是使数学获得新生的源泉。——伯克霍夫
如图,正方形ABCD的边长为8厘米,长方形EBGF的长BG为10厘米。求长方形的宽。
【解析】连接AG,则可以依据题目条件求出三角形AGB的面积,因为DG已知,进而可以求三角形AGD的高,也就是长方形的宽,问题得解。
解答:长方形的宽的长是6.4厘米。
如图已知正方形ABCD和正方形DEFM,且正方形ABCD的边长为8分米。请问图中阴影部分的面积是多少平方分米?
【解析】连结FD。根据等底等高的三角形面积相等可得S△AFD=S△FDC,而△FHD是它们的公共部分,因此,△AHD与△HCD的面积相等,从而得到△AFC=S△AHC+S△HCD=S△ADC=0。正方形ABCD面积依此即可求。
解答:图中阴影部分的面积是32平方分米。
如图,已知梯形ABCD的面积为5,DA与EB平行,ED与CA平行,求四边形EDAC的面积。
【解析】连接EA、DB,根据平行线间的距离处处相等,和等底等高的三角形的面积相等,可得△EDC的面积=△EDA的面积、△EDA的面积=△DAB的面积、△DAB的面积=△CAB的面积;据此可得△EDC的面积=△CAB的面积;据此可得四边形EDAC的面积=△EDC的面积+△CDA的面积=△CAB的面积+△CDA的面积=梯形ABCD的面积=5。
解答:四边形EDAC的面积是5。
如图△ABC中,E、D、G分别是AB、BC、AD的中点,图中与△ADE等积的三角形一共有多少个?
【解析】三角形的面积等于底乘高除以2,所以只要是等底、等高的三角形面积就都相等。E是AB的中点,△ADE与△BDE等底、等高,面积相等;D是BC的中点,△ABD与△ADC等底、等高,面积相等,△ADE与△BDE是△ABD面积的一半,△DCG与△AGC是△ADC的一半;又G是AD的中点,△DCG与△AGC等底、等高,面积相等;所以与△ADE面积相等的三角形有:△BDE、△DCG、△AGC共有3个。
解答:图中与△ADE等积的三角形一共有3个。
如图,在△ABC中,EF∥BC,AB=3AE,那么三角形甲、乙、丙面积的连比是多少?
【解析】先比较甲和乙的面积,再比较(甲+乙)和丙的面积。
解答:甲、乙、丙面积的连比是1:2:6。
在图中,△ABC的面积是52,AC=13,△FDC是等腰直角三角形,又△ADC与△ABD面积相等,求△ADF的面积是多少?
【解析】△ABC若以BC为底,△ABD以BD为底,△ACD以CD为底,则它们的高相等,△ADC与△ABD面积相等都是26,根据三角形的面积公式可知它们的底也相等,即BD=CD;△ADC以AC为底,那么DF就是AC边上的高,根据它的面积和AC的长度就可以求出DF的长度,进而可求AF的长度,再根据直角三角形的面积公式就可以求出△ADF的面积。
因为S△ABC=52,所以S△ADC=S△ABD=52÷2=26;又因为AC=13,△FDC是等腰直角三角形,所以DF=S△ADC×2÷AC=26×2÷13=4;
因为CF=DF,即CF=4,所以AF=AC-CF=13-4=9;S△ADF=4×9÷2=18。
解答:△ADF的面积是18。
如图,在平行四边形ABCD中,E为BC的中点,DF=2BF,三角形BEF(图中阴影部分)的面积是8平方厘米。求:平行四边形的面积。
【解析】边接CF,△BFE与△CEF的高相同,面积的比就是底的比,E为BC的中点。所以它们面积的比为1:1,△CEF的面积为就是8平方厘米,△BCF与△CDF的高相同,它们面积的比就是底的比,因DF=2BF,所以它们面积的比是2:1,△CDF的面积是32平方厘米,平行四边形ABCD的面积等于三角形BCD的面积2倍。据此可求出平行四边形的面积。
解答:平行四边形的面积是96平方厘米。
长方形ABCD的对角线AC、BD相交于点O,过点O的直线分别交AD、BC于点E、F, AB=2厘米,BC=3厘米,问图中阴影部分的面积是多少平方厘米?
【解析】阴影部分的面积等于空白部分的面积。
解答:阴影部分的面积是3平方厘米。
如图,边长为7的正方形ABCD和边长为5的正方形CEFG并排放在一起,O1和O2分别是两个正方形的中心(正方形对角线的交点),问阴影部分的面积是多少?
【解析】连接CO1 ,CO2 ,我们发现CO2 和O1B平行,那么△O1O2 B和△O1CB的面积相等,所以△BO2 P和△O1PC的面积相等。
解答:阴影部分的面积=7×(7÷2)÷2=12.25。
如图,四边形EFGH的面积是66平方米,EA=AB,CB=BF,DC=CG,HD=DA。求四边形ABCD的面积。
【解析】根据四边形ABCD的面积是66平方米,要求四边形ABCD的面积,只要求出四边形ABCD与四周多出来的四个三角形的面积的关系以及四边形ABCD与四边形EFGH的面积关系,即可解决问题。
连接CA、AF、HC,则三角形ADC的面积=三角形HDC的面积=三角形HCG的面积=三角形HDG的面积的一半,同理可得,ABCD的面积为13.2平方米。
解答:四边形ABCD的面积为13.2平方米。
数学名言(一)
数统治着宇宙。 ——毕达哥拉斯
数学,科学的女皇;数论,数学的女皇。 ——高斯
上帝创造了整数,所有其余的数都是人造的。 ——克隆内克
上帝是一位算术家。 ——雅克比
一个没有几分诗人气的数学家永远成不了一个完全的数学家。——维尔斯特拉斯
纯数学这门科学在其现代发展阶段,可以说是人类精神之最具独创性的创造。——怀德海
整数的简单构成,若干世纪以来一直是使数学获得新生的源泉。——伯克霍夫
同课章节目录
