六年级上册数学讲义小升初培优第09讲 图形计数 (解析版)全国通用
文档属性
| 名称 | 六年级上册数学讲义小升初培优第09讲 图形计数 (解析版)全国通用 |  | |
| 格式 | doc | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 11:15:23 | ||
图片预览


文档简介
第九讲 图形计数
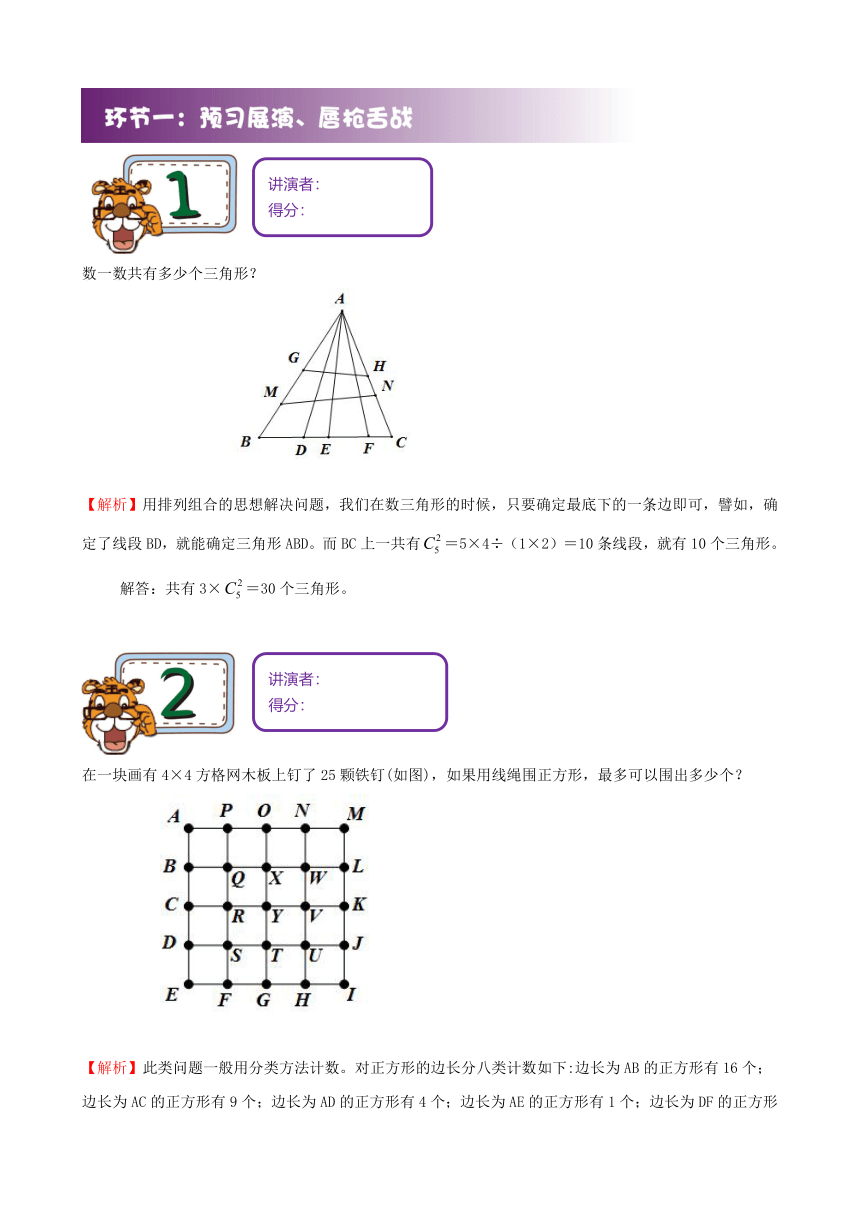
数一数共有多少个三角形?
【解析】用排列组合的思想解决问题,我们在数三角形的时候,只要确定最底下的一条边即可,譬如,确定了线段BD,就能确定三角形ABD。而BC上一共有=5×4÷(1×2)=10条线段,就有10个三角形。
解答:共有3×=30个三角形。
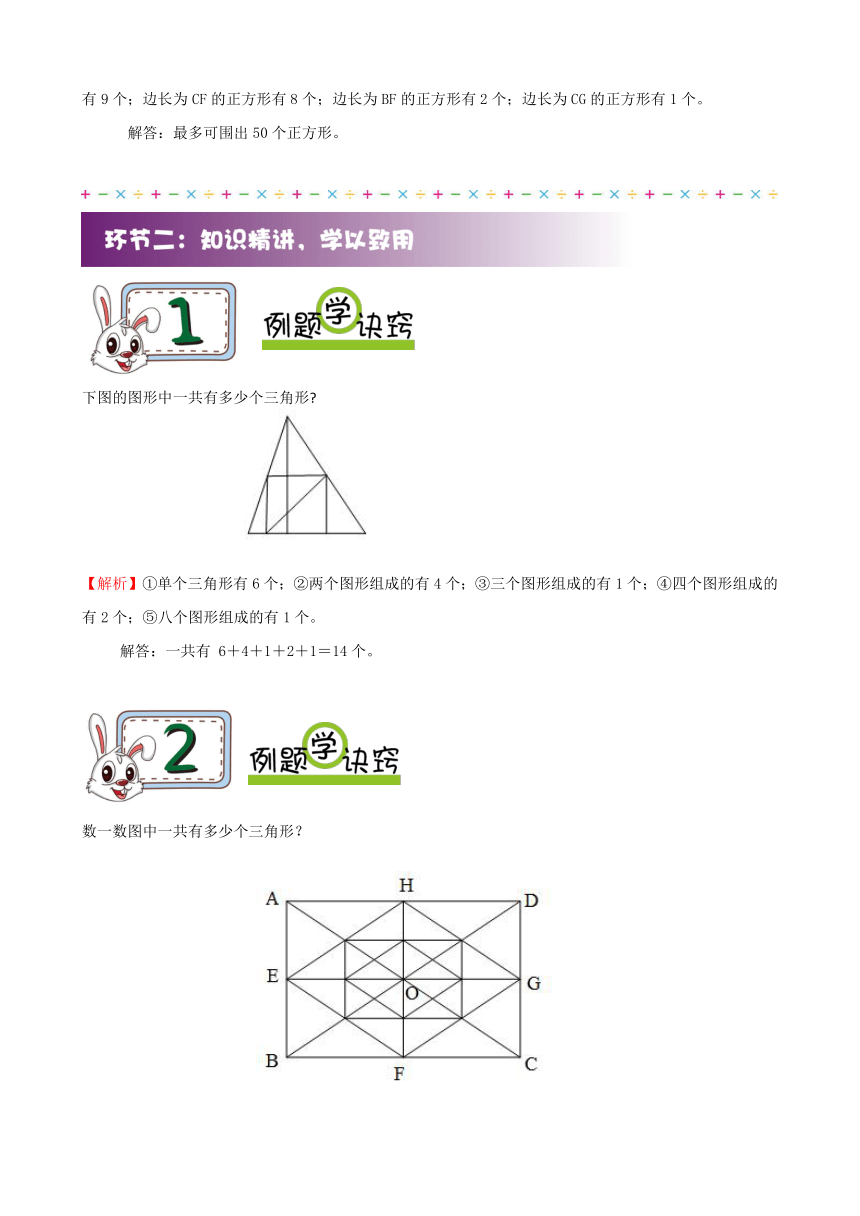
在一块画有4×4方格网木板上钉了25颗铁钉(如图),如果用线绳围正方形,最多可以围出多少个?
【解析】此类问题一般用分类方法计数。对正方形的边长分八类计数如下:边长为AB的正方形有16个;边长为AC的正方形有9个;边长为AD的正方形有4个;边长为AE的正方形有1个;边长为DF的正方形有9个;边长为CF的正方形有8个;边长为BF的正方形有2个;边长为CG的正方形有1个。
解答:最多可围出50个正方形。
下图的图形中一共有多少个三角形?
【解析】①单个三角形有6个;②两个图形组成的有4个;③三个图形组成的有1个;④四个图形组成的有2个;⑤八个图形组成的有1个。
解答:一共有 6+4+1+2+1=14个。
数一数图中一共有多少个三角形?
【解析】分析这是个对称图形,我们可按如下三步顺序来数:第一步:大矩形ABCD可分为四个相同的小矩形:AEOH、EBFO、OFCG、HOGD,每个小矩形内所包含的三角形个数是相同的。第二步:每两个小矩形组合成的图形共有四个,如:ABFH、EBCG、HFCD、AEGD,每一个这样的图形中所包含的三角形个数是相同的。第三步:每三个小矩形占据的部分图形共有四个:如△ABD、△ADC、△ABC、△DBC,每一个这样的图形中所包含的三角形个数是相同的。最后把每个图形所包含三角形个数求出相加再乘以4就是整个图形中所包含的三角形的个数。
解答:Ⅰ.在小矩形AEOH中:①由一个三角形构成的有8个;②由两个三角形构成的三角形有5个;③由三个或三个以上三角形构成的三角形有5个这样在一个小矩形内有17个三角形。
Ⅱ.在由两个小矩形组合成的图形中,如矩形AEGD,共有5个三角形。
Ⅲ.由三个小矩形占据的部分图形中,如△ABC,共有2个三角形。
所以整个图形共有三角形个数是:(8+5+5+5+2)×=25×4=100(个)。
由35个单位正方形组成的长方形中,如图所示有两个“A”,问包含两个“A”在内的由小正方形组成的长方形(含正方形)有多少?
【解析】方法一:含两个A的长方形,与二,三两行有公共部分。它们可能与第一行有公共部分,也可能与第一行没有有公共部分,故可以分为两类;每一类的长方形,可能和第四,五两行有公共部分,或都没有公共部分,或仅与第四行有公共部分,而与第五行没有公共部分,即又分为三类。故从行考虑共有(2×3)种方法;同理,从列来考虑有(3×4)种方法;于是,含两个“A”在内的由小正方形组成的长方形(含正方形)有(2×3)×(3×4)=72个。
方法二:要确定一个符合条件的长方形,需要有上下左右四条边。选择上边所在的直线,有2种方法;选择下边所在的直线,有3种方法;选择左边所在的直线,有3种方法;选择右边所在的直线,有4种方法。于是,含两个“A”在内的由小正方形组成的长方形(含正方形)有2×3×3×4=72个。
解答:72个。
8条直线最多能把平面分成多少部分?
【解析】1条直线最多将平面分成2个部分;2条直线最多将平面分成4个部分;3条直线最多将平面分成7个部分;现在添上第4条直线.它与前面的3条直线最多有3个交点,这3个交点将第4条直线分成4段,其中每一段将原来所在平面部分一分为二,如图,所以4条直线最多将平面分成7+4=11个部分。完全类似地,5条直线最多将平面分成11+5=16个部分;6条直线最多将平面分16+6=22个部分;7条直线最多将平面分成22+7=29个部分;8条直线最多将平面分成29+8=37个部分。
一般地,n条直线最多将平面分成个部分。
解答:8条直线最多能把平面分成37部分。
10个三角形最多能将平面分成几个部分?
【解析】设n个三角形最多将平面分成an个部分。画图枚举说明。n=1时,a1=2;n=2时,第二个三角形的每一条边与第一个三角形最多有2个交点,三条边与第一个三角形最多有2×3=6(个)交点。这6个交点将第二个三角形的周边分成了6段,这6段中的每一段都将原来的每一个部分分成2个部分,从而平面也增加了6个部分,即a2=2+2×3。n=3时,第三个三角形与前面两个三角形最多有4×3=12(个)交点,从而平面也增加了12个部分,即:a3=2+2×3+4×3。一般地,第n个三角形与前面(n-1)个三角形最多有2(n-1)×3个交点,从而平面也增加2(n-1)×3个部分,故an=2+2×3+4×3+…+2(n-1)×3=2+[2+4+…+2(n-1)]×3=2+3n(n-1)=3n2-3n+2。
特别地,当n=10时,a10=3×102+3×10+2=272,即10个三角形最多把平面分成272个部分。
解答:272个部分。
下面三个图中分别有多少个三角形?
图一 图二
【解析】图二再图一的基础上去做加减。图二是图一的个数减去与少去的那条线段相关的三角形的个数。
解答:图一35个;图二29个。
如下左图,方格纸上放了20枚棋子,以棋子为顶点的正方形共有多少个?
【解析】以正方形的面积大小分类计数。设相邻两点的距离为1,则正方形面积为1的有9个;面积为2的有4个;面积为5的有2个;面积为8的有4个;面积为13的有2个。
解答:共有9+4+2+4+2=21个正方形。
在一个8×8的方格棋盘中,有多少个由4个小方格组成的“凸”字形图形?
【解析】在每个2×3的长方形中可以找到2个“凸”字形图形。而在6×6方格棋盘中2×3的长方形有(4×5)×2=40(个)。所以可以找到40×2=80个“凸”字形图形。
解答:有80个由4个小方格组成的“凸”字形图形。
熊庆来的故事
熊庆来的父亲熊国栋,精通儒学,但更喜欢新学,思想很开明,对熊庆来的影响很大。少年时的熊庆来从他父亲那里常听到有关孙中山民主革命的事情,这在幼年熊庆来的心田播下了爱国的种子。
1907年,熊庆来考入昆明的云南方言学堂,不久又升入云南高等学堂。当时满清王朝已日薄西山,各地的反清斗争风起云涌,抗捐、抗税、罢课、罢市、兵变遍及全国,清政府陷入于风雨飘摇之中。熊庆来由于参加了“收回矿山开采权”的抗法反清示威游行,而遭到学校的记过处分。现实的生活与斗争使名熊庆来认识到:要使国家富强,必须掌握科学,科学能强国富民。
1913年,熊庆来赴欧留学。1914年,第一次世界大战爆发,他从比利时经荷兰、英国,辗转到了法国巴黎。8年间先后获得高等数学、力学及天文学等多科证书,并获得理学硕士学位。1921年,28岁的熊庆来学成归国,一心想学以致用,救民于水火。1949年6月,国民党反动政府趁熊庆来去巴黎参加国际会议的机会,解散了熊庆来苦心经营12年的云南大学。年近花甲的熊庆来怀着“壮志难酬、报国无门”的心情,决定滞留在法国继续从事函数论的研究。
“……祖国欢迎你,人民欢迎你!欢迎你回来参加社会主义建设的伟大事业……”1957年4月,周总理给熊庆来写信,动员他回国。同年6月,熊庆来在完成了函数论专著稿后,毅然启程,回到了祖国的怀抱。他表示,愿在社会主义的光芒中鞠躬尽瘁于祖国的学术建设事业。在回国后的7年中,他在国内外学术杂志上发表了近20篇具有世界水平的数学论文,还培养了杨乐、张广厚等一批数学人才,为祖国赢得了荣誉,表现了这位七旬老人热爱祖国的赤子之心。
数一数共有多少个三角形?
【解析】用排列组合的思想解决问题,我们在数三角形的时候,只要确定最底下的一条边即可,譬如,确定了线段BD,就能确定三角形ABD。而BC上一共有=5×4÷(1×2)=10条线段,就有10个三角形。
解答:共有3×=30个三角形。
在一块画有4×4方格网木板上钉了25颗铁钉(如图),如果用线绳围正方形,最多可以围出多少个?
【解析】此类问题一般用分类方法计数。对正方形的边长分八类计数如下:边长为AB的正方形有16个;边长为AC的正方形有9个;边长为AD的正方形有4个;边长为AE的正方形有1个;边长为DF的正方形有9个;边长为CF的正方形有8个;边长为BF的正方形有2个;边长为CG的正方形有1个。
解答:最多可围出50个正方形。
下图的图形中一共有多少个三角形?
【解析】①单个三角形有6个;②两个图形组成的有4个;③三个图形组成的有1个;④四个图形组成的有2个;⑤八个图形组成的有1个。
解答:一共有 6+4+1+2+1=14个。
数一数图中一共有多少个三角形?
【解析】分析这是个对称图形,我们可按如下三步顺序来数:第一步:大矩形ABCD可分为四个相同的小矩形:AEOH、EBFO、OFCG、HOGD,每个小矩形内所包含的三角形个数是相同的。第二步:每两个小矩形组合成的图形共有四个,如:ABFH、EBCG、HFCD、AEGD,每一个这样的图形中所包含的三角形个数是相同的。第三步:每三个小矩形占据的部分图形共有四个:如△ABD、△ADC、△ABC、△DBC,每一个这样的图形中所包含的三角形个数是相同的。最后把每个图形所包含三角形个数求出相加再乘以4就是整个图形中所包含的三角形的个数。
解答:Ⅰ.在小矩形AEOH中:①由一个三角形构成的有8个;②由两个三角形构成的三角形有5个;③由三个或三个以上三角形构成的三角形有5个这样在一个小矩形内有17个三角形。
Ⅱ.在由两个小矩形组合成的图形中,如矩形AEGD,共有5个三角形。
Ⅲ.由三个小矩形占据的部分图形中,如△ABC,共有2个三角形。
所以整个图形共有三角形个数是:(8+5+5+5+2)×=25×4=100(个)。
由35个单位正方形组成的长方形中,如图所示有两个“A”,问包含两个“A”在内的由小正方形组成的长方形(含正方形)有多少?
【解析】方法一:含两个A的长方形,与二,三两行有公共部分。它们可能与第一行有公共部分,也可能与第一行没有有公共部分,故可以分为两类;每一类的长方形,可能和第四,五两行有公共部分,或都没有公共部分,或仅与第四行有公共部分,而与第五行没有公共部分,即又分为三类。故从行考虑共有(2×3)种方法;同理,从列来考虑有(3×4)种方法;于是,含两个“A”在内的由小正方形组成的长方形(含正方形)有(2×3)×(3×4)=72个。
方法二:要确定一个符合条件的长方形,需要有上下左右四条边。选择上边所在的直线,有2种方法;选择下边所在的直线,有3种方法;选择左边所在的直线,有3种方法;选择右边所在的直线,有4种方法。于是,含两个“A”在内的由小正方形组成的长方形(含正方形)有2×3×3×4=72个。
解答:72个。
8条直线最多能把平面分成多少部分?
【解析】1条直线最多将平面分成2个部分;2条直线最多将平面分成4个部分;3条直线最多将平面分成7个部分;现在添上第4条直线.它与前面的3条直线最多有3个交点,这3个交点将第4条直线分成4段,其中每一段将原来所在平面部分一分为二,如图,所以4条直线最多将平面分成7+4=11个部分。完全类似地,5条直线最多将平面分成11+5=16个部分;6条直线最多将平面分16+6=22个部分;7条直线最多将平面分成22+7=29个部分;8条直线最多将平面分成29+8=37个部分。
一般地,n条直线最多将平面分成个部分。
解答:8条直线最多能把平面分成37部分。
10个三角形最多能将平面分成几个部分?
【解析】设n个三角形最多将平面分成an个部分。画图枚举说明。n=1时,a1=2;n=2时,第二个三角形的每一条边与第一个三角形最多有2个交点,三条边与第一个三角形最多有2×3=6(个)交点。这6个交点将第二个三角形的周边分成了6段,这6段中的每一段都将原来的每一个部分分成2个部分,从而平面也增加了6个部分,即a2=2+2×3。n=3时,第三个三角形与前面两个三角形最多有4×3=12(个)交点,从而平面也增加了12个部分,即:a3=2+2×3+4×3。一般地,第n个三角形与前面(n-1)个三角形最多有2(n-1)×3个交点,从而平面也增加2(n-1)×3个部分,故an=2+2×3+4×3+…+2(n-1)×3=2+[2+4+…+2(n-1)]×3=2+3n(n-1)=3n2-3n+2。
特别地,当n=10时,a10=3×102+3×10+2=272,即10个三角形最多把平面分成272个部分。
解答:272个部分。
下面三个图中分别有多少个三角形?
图一 图二
【解析】图二再图一的基础上去做加减。图二是图一的个数减去与少去的那条线段相关的三角形的个数。
解答:图一35个;图二29个。
如下左图,方格纸上放了20枚棋子,以棋子为顶点的正方形共有多少个?
【解析】以正方形的面积大小分类计数。设相邻两点的距离为1,则正方形面积为1的有9个;面积为2的有4个;面积为5的有2个;面积为8的有4个;面积为13的有2个。
解答:共有9+4+2+4+2=21个正方形。
在一个8×8的方格棋盘中,有多少个由4个小方格组成的“凸”字形图形?
【解析】在每个2×3的长方形中可以找到2个“凸”字形图形。而在6×6方格棋盘中2×3的长方形有(4×5)×2=40(个)。所以可以找到40×2=80个“凸”字形图形。
解答:有80个由4个小方格组成的“凸”字形图形。
熊庆来的故事
熊庆来的父亲熊国栋,精通儒学,但更喜欢新学,思想很开明,对熊庆来的影响很大。少年时的熊庆来从他父亲那里常听到有关孙中山民主革命的事情,这在幼年熊庆来的心田播下了爱国的种子。
1907年,熊庆来考入昆明的云南方言学堂,不久又升入云南高等学堂。当时满清王朝已日薄西山,各地的反清斗争风起云涌,抗捐、抗税、罢课、罢市、兵变遍及全国,清政府陷入于风雨飘摇之中。熊庆来由于参加了“收回矿山开采权”的抗法反清示威游行,而遭到学校的记过处分。现实的生活与斗争使名熊庆来认识到:要使国家富强,必须掌握科学,科学能强国富民。
1913年,熊庆来赴欧留学。1914年,第一次世界大战爆发,他从比利时经荷兰、英国,辗转到了法国巴黎。8年间先后获得高等数学、力学及天文学等多科证书,并获得理学硕士学位。1921年,28岁的熊庆来学成归国,一心想学以致用,救民于水火。1949年6月,国民党反动政府趁熊庆来去巴黎参加国际会议的机会,解散了熊庆来苦心经营12年的云南大学。年近花甲的熊庆来怀着“壮志难酬、报国无门”的心情,决定滞留在法国继续从事函数论的研究。
“……祖国欢迎你,人民欢迎你!欢迎你回来参加社会主义建设的伟大事业……”1957年4月,周总理给熊庆来写信,动员他回国。同年6月,熊庆来在完成了函数论专著稿后,毅然启程,回到了祖国的怀抱。他表示,愿在社会主义的光芒中鞠躬尽瘁于祖国的学术建设事业。在回国后的7年中,他在国内外学术杂志上发表了近20篇具有世界水平的数学论文,还培养了杨乐、张广厚等一批数学人才,为祖国赢得了荣誉,表现了这位七旬老人热爱祖国的赤子之心。
同课章节目录
