六年级上册数学讲义小升初培优第09讲 格点面积(解析版)全国通用
文档属性
| 名称 | 六年级上册数学讲义小升初培优第09讲 格点面积(解析版)全国通用 |  | |
| 格式 | doc | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 11:16:43 | ||
图片预览


文档简介
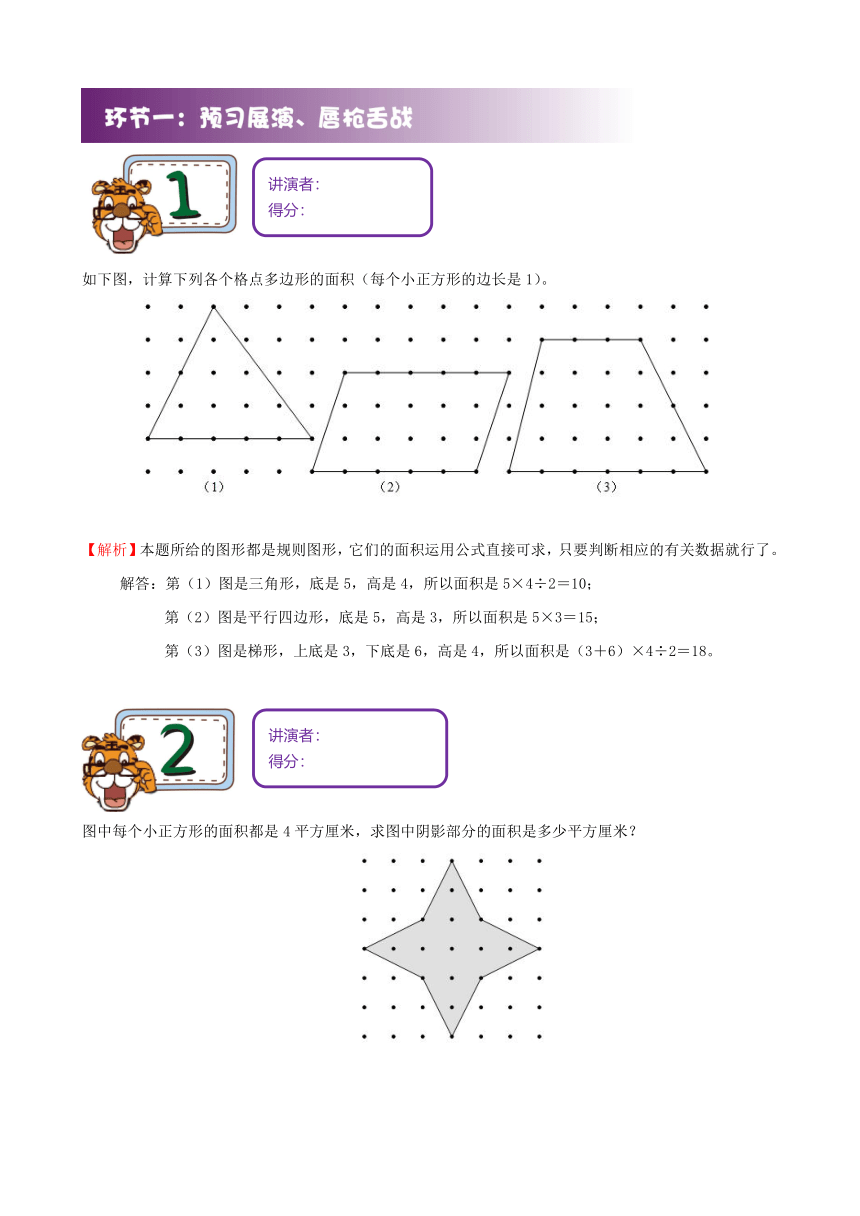
第九讲 格点面积
如下图,计算下列各个格点多边形的面积(每个小正方形的边长是1)。
【解析】本题所给的图形都是规则图形,它们的面积运用公式直接可求,只要判断相应的有关数据就行了。
解答:第(1)图是三角形,底是5,高是4,所以面积是5×4÷2=10;
第(2)图是平行四边形,底是5,高是3,所以面积是5×3=15;
第(3)图是梯形,上底是3,下底是6,高是4,所以面积是(3+6)×4÷2=18。
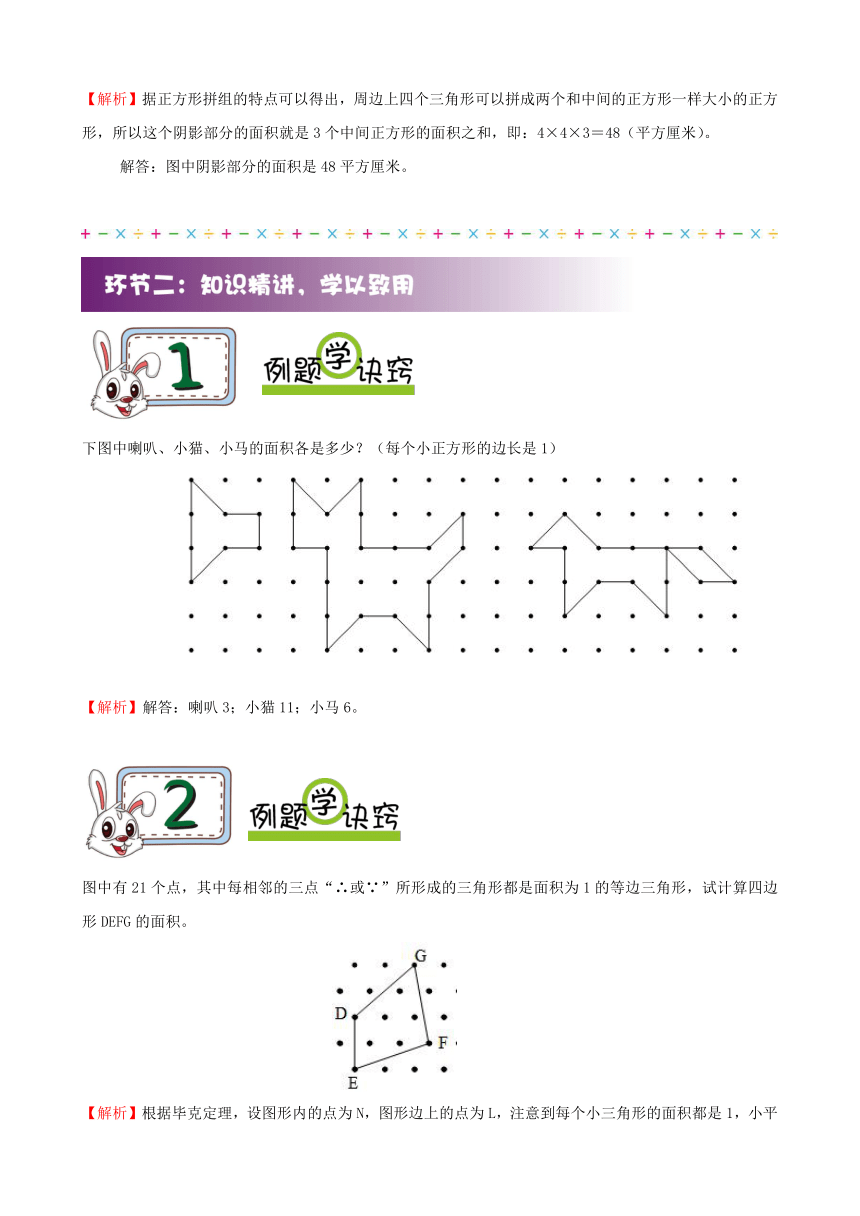
图中每个小正方形的面积都是4平方厘米,求图中阴影部分的面积是多少平方厘米?
【解析】据正方形拼组的特点可以得出,周边上四个三角形可以拼成两个和中间的正方形一样大小的正方形,所以这个阴影部分的面积就是3个中间正方形的面积之和,即:4×4×3=48(平方厘米)。
解答:图中阴影部分的面积是48平方厘米。
下图中喇叭、小猫、小马的面积各是多少?(每个小正方形的边长是1)
【解析】解答:喇叭3;小猫11;小马6。
图中有21个点,其中每相邻的三点“∴或∵”所形成的三角形都是面积为1的等边三角形,试计算四边形DEFG的面积。
【解析】根据毕克定理,设图形内的点为N,图形边上的点为L,注意到每个小三角形的面积都是1,小平行四边形的面积为2,则面积为2(N +L÷2-1)。①内部格点数为:5个;②周界上格点数为:4个;③阴影部分的面积是:2×(4÷2+5-1)=12(面积单位)。
解答:四边形DEFG的面积为12面积单位。
把大正三角形每边八等份,组成如下图所示的三角形网。如果每个小三角形的面积都是1,求图中粗线所围成的三角形的面积。
【解析】根据毕克定理,设图形内的点为N,图形边上的点为L,注意到每个小三角形的面积都是1,小平行四边形的面积为2,则面积为2(L÷2-1+N)。①内部格点数为:12个;②周界上格点数为:4个;
③阴影部分的面积是:2×(4÷2+12-1)=26(平方厘米)。
解答:图中粗线所围成的三角形的面积为26平方厘米。
在图中,如果钉与钉之间距离为1厘米,用橡皮筋将适当的三个钉子连接起来就得到一个三角形。在这些三角形中,面积等于2平方厘米的三角形有多少个?
【解析】由题意可得:要求面积等于2平方厘米的三角形有几个,可以分别找出以AC为底边、AF为底边、FH为底边、CH为底边的符合条件的三角形各有几个;然后相加即可;如图,
以AC为底边的面积是2平方厘米的三角形有:△ACF,△ACG,△ACH,3个;
FH为底边的面积是2平方厘米的三角形有:△FHA,△FHB,△FHC,3个;
AF为底边面积是2平方厘米的三角形有(不重复):△AFD,1个;
CH为底边面积等于2平方厘米的三角形(不重复):△CHE,1个;共有:3+3+1=1=8(个 );
解答:面积等于2平方厘米的三角形有8个。
下图是一个5×5的方格纸,小方格的面积是1平方厘米,小方格的顶点为格点。请你在图上选7个格点,要求其中任意3个格点都不在一条直线上,并且使这7个点用线段连接所围成的面积尽可能大,那么,这个最大的面积是多少平方厘米?
【解析】这是一个5×5的方格纸,共有25个格点。现在要围成一个面积最大的图形,根据格点面积公式,要使图形面积最大,必须使图形包含的内部格点数和周界上格点数尽可能多。由方格纸可知,内部格点数最多为4×4=16,周界上格点数最多为5×4=20。但是,当周界上格点数为最多时,不符合题中“任意3个格点不在一条直线上”的条件,因此,适当调整图上7个格点的位置,如下图所示,就得到了面积最大的图形。7个格点分布如下图:所围成图形的最大面积为:5×5-0.5×3=23.5(平方厘米)。
解答:最大的面积是23.5平方厘米。
图中49个小正三角形的面积都等于1,求阴影部分的面积。
【解析】解答:16。
如图是某海岸一个灯塔的平面图。已知它的面积为23个单位,求塔图内部的格点数。
【解析】我们完全可以画出内部的格点,再数一数知它们有多少个点,这是直接法。但有了毕克定理后还可间接地去求。根据毕克定理S=N+L÷2-1,现已知S=23,数一数边界上的格点可知L=30,23=N+30÷2-1,易求得N=9。
解答:塔图内部有9个格点。
你知道下图中共有多少个图形吗?四边形ADBC的面积是多少?(每个小正方形的边长是1)
【解析】这里所说的图形既包括凸多边形,也包括凹多边形。图中有8个三角形AEC,AED,ADC,ABD,ABC,EBD,EBC,DBC;有3个四边形:ADBC,ABDC,ABCD。可以用毕克公式算出每个图形的面积,例如四边形ADBC的面积为:21+8÷2-1=24。
解答:有11个图形;四边形ADBC的面积是24。
数学名言(二)
算数的四则运算可以看作是数学家的全部装备。——麦克斯韦
数论是人类知识最古老的一个分支,然而他的一些最深奥的秘密与其最平凡的真理是密切相连的。
——史密斯
无限!再也没有其他问题如此深刻地打动过人类的心灵。——希尔伯特
发现每一个新的群体在形式上都是数学的,因为我们不可能有其他的指导。——达尔文
宇宙的伟大建筑是现在开始以纯数学家的面目出现了。——京斯
这是一个可靠的规律,当数学或哲学著作的作者以模糊深奥的话写作时,他是在胡说八道。
——怀德海
给我五个系数,我将画出一头大象;给我六个系数,大象将会摇动尾巴。——柯西
纯数学是魔术家真正的魔杖。——诺瓦列斯
如下图,计算下列各个格点多边形的面积(每个小正方形的边长是1)。
【解析】本题所给的图形都是规则图形,它们的面积运用公式直接可求,只要判断相应的有关数据就行了。
解答:第(1)图是三角形,底是5,高是4,所以面积是5×4÷2=10;
第(2)图是平行四边形,底是5,高是3,所以面积是5×3=15;
第(3)图是梯形,上底是3,下底是6,高是4,所以面积是(3+6)×4÷2=18。
图中每个小正方形的面积都是4平方厘米,求图中阴影部分的面积是多少平方厘米?
【解析】据正方形拼组的特点可以得出,周边上四个三角形可以拼成两个和中间的正方形一样大小的正方形,所以这个阴影部分的面积就是3个中间正方形的面积之和,即:4×4×3=48(平方厘米)。
解答:图中阴影部分的面积是48平方厘米。
下图中喇叭、小猫、小马的面积各是多少?(每个小正方形的边长是1)
【解析】解答:喇叭3;小猫11;小马6。
图中有21个点,其中每相邻的三点“∴或∵”所形成的三角形都是面积为1的等边三角形,试计算四边形DEFG的面积。
【解析】根据毕克定理,设图形内的点为N,图形边上的点为L,注意到每个小三角形的面积都是1,小平行四边形的面积为2,则面积为2(N +L÷2-1)。①内部格点数为:5个;②周界上格点数为:4个;③阴影部分的面积是:2×(4÷2+5-1)=12(面积单位)。
解答:四边形DEFG的面积为12面积单位。
把大正三角形每边八等份,组成如下图所示的三角形网。如果每个小三角形的面积都是1,求图中粗线所围成的三角形的面积。
【解析】根据毕克定理,设图形内的点为N,图形边上的点为L,注意到每个小三角形的面积都是1,小平行四边形的面积为2,则面积为2(L÷2-1+N)。①内部格点数为:12个;②周界上格点数为:4个;
③阴影部分的面积是:2×(4÷2+12-1)=26(平方厘米)。
解答:图中粗线所围成的三角形的面积为26平方厘米。
在图中,如果钉与钉之间距离为1厘米,用橡皮筋将适当的三个钉子连接起来就得到一个三角形。在这些三角形中,面积等于2平方厘米的三角形有多少个?
【解析】由题意可得:要求面积等于2平方厘米的三角形有几个,可以分别找出以AC为底边、AF为底边、FH为底边、CH为底边的符合条件的三角形各有几个;然后相加即可;如图,
以AC为底边的面积是2平方厘米的三角形有:△ACF,△ACG,△ACH,3个;
FH为底边的面积是2平方厘米的三角形有:△FHA,△FHB,△FHC,3个;
AF为底边面积是2平方厘米的三角形有(不重复):△AFD,1个;
CH为底边面积等于2平方厘米的三角形(不重复):△CHE,1个;共有:3+3+1=1=8(个 );
解答:面积等于2平方厘米的三角形有8个。
下图是一个5×5的方格纸,小方格的面积是1平方厘米,小方格的顶点为格点。请你在图上选7个格点,要求其中任意3个格点都不在一条直线上,并且使这7个点用线段连接所围成的面积尽可能大,那么,这个最大的面积是多少平方厘米?
【解析】这是一个5×5的方格纸,共有25个格点。现在要围成一个面积最大的图形,根据格点面积公式,要使图形面积最大,必须使图形包含的内部格点数和周界上格点数尽可能多。由方格纸可知,内部格点数最多为4×4=16,周界上格点数最多为5×4=20。但是,当周界上格点数为最多时,不符合题中“任意3个格点不在一条直线上”的条件,因此,适当调整图上7个格点的位置,如下图所示,就得到了面积最大的图形。7个格点分布如下图:所围成图形的最大面积为:5×5-0.5×3=23.5(平方厘米)。
解答:最大的面积是23.5平方厘米。
图中49个小正三角形的面积都等于1,求阴影部分的面积。
【解析】解答:16。
如图是某海岸一个灯塔的平面图。已知它的面积为23个单位,求塔图内部的格点数。
【解析】我们完全可以画出内部的格点,再数一数知它们有多少个点,这是直接法。但有了毕克定理后还可间接地去求。根据毕克定理S=N+L÷2-1,现已知S=23,数一数边界上的格点可知L=30,23=N+30÷2-1,易求得N=9。
解答:塔图内部有9个格点。
你知道下图中共有多少个图形吗?四边形ADBC的面积是多少?(每个小正方形的边长是1)
【解析】这里所说的图形既包括凸多边形,也包括凹多边形。图中有8个三角形AEC,AED,ADC,ABD,ABC,EBD,EBC,DBC;有3个四边形:ADBC,ABDC,ABCD。可以用毕克公式算出每个图形的面积,例如四边形ADBC的面积为:21+8÷2-1=24。
解答:有11个图形;四边形ADBC的面积是24。
数学名言(二)
算数的四则运算可以看作是数学家的全部装备。——麦克斯韦
数论是人类知识最古老的一个分支,然而他的一些最深奥的秘密与其最平凡的真理是密切相连的。
——史密斯
无限!再也没有其他问题如此深刻地打动过人类的心灵。——希尔伯特
发现每一个新的群体在形式上都是数学的,因为我们不可能有其他的指导。——达尔文
宇宙的伟大建筑是现在开始以纯数学家的面目出现了。——京斯
这是一个可靠的规律,当数学或哲学著作的作者以模糊深奥的话写作时,他是在胡说八道。
——怀德海
给我五个系数,我将画出一头大象;给我六个系数,大象将会摇动尾巴。——柯西
纯数学是魔术家真正的魔杖。——诺瓦列斯
同课章节目录
