锐角三角函数复习课

(共12张PPT)
总复习：锐角三角函数
制作者：彭贵金
复习：锐角三角函数
制作者：彭贵金
一、本节课的复习内容：
1.掌握锐角三角函数的定义。
2.掌握同角或互余两角间的三角函数关系并会用它求值。
3.熟记的各种三角函数值，会计算含有特殊角的三角函数式的值，会由一个特殊锐角的三角函数值，求出相应的角。
1、锐角三角函数
1.定义：在直角三角形中，一个锐角为∠A，SinA、CosA、tanA分别叫做∠A的正弦、余弦、正切。锐角的正弦、余弦、正切统称为锐角三角函数。
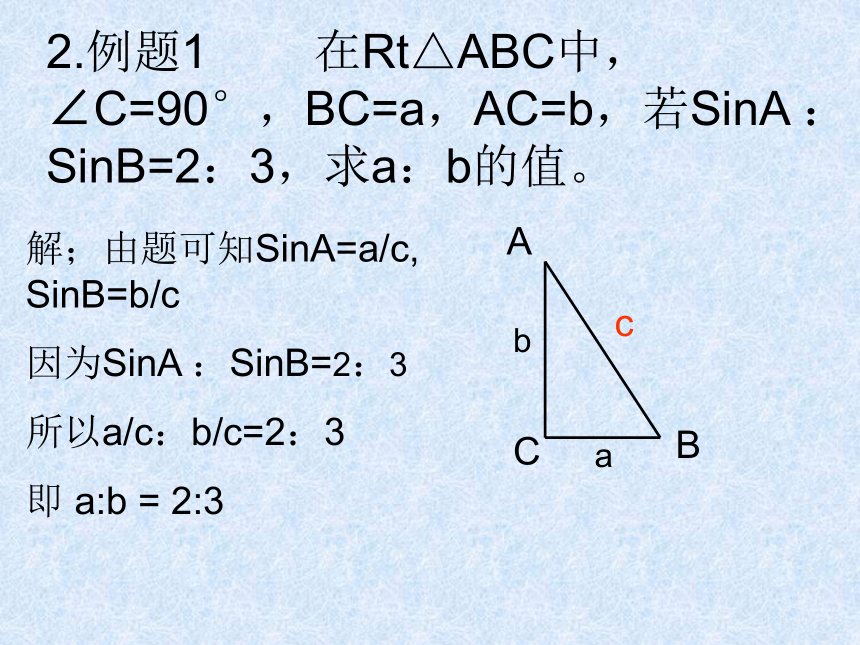
2.例题1 在Rt△ABC中，∠C=90°，BC=a，AC=b，若SinA ：SinB=2：3，求a：b的值。
A
B
C
a
b
c
解；由题可知SinA=a/c, SinB=b/c
因为SinA ：SinB=2：3
所以a/c：b/c=2：3
即 a:b = 2:3
例2、在Rt△ABC中， ∠C=90°， SinA=4/5，求CosA、tanA的值。
解：如图，因为SinA=4/5，
所以设 BC=4k ，AB=5k
由勾股定理得AC=3k
所以CosA = AC/AB = 3k/5k =3/5
tanA = 4k/3k = 4/3
2、同角三角函数之间的关系：
① Sin A + Cos A = 1
2
2
② tanA = SinA/CosA
3、互余两角三角函数之间的关系：
SinA = Cos（90°-A）
CosA = Sin （90°-A）
例3、在△ABC中， ∠C=90°化简下面的式子：√1-2 SinA CosA
解： √1-2 SinA CosA = √ Sin A - 2 SinA CosA + Cos A
=√（ Sin A - Cos A）
=∣ SinA- CosA∣
————————-——-
————————-
————————————————
2
2
2
——————————--
4、三角函数值的变化规律：
填空：比较大小
(1) tan35°17′___ tan17°35′
(2) Cos9 °____ Cos10°
(3) Sin68° ____ Sin82°
(4) Sin35° ____ Cos25°
﹥
﹥
﹤
﹤
攻略：正弦、正切值随角度的增加而增大，余弦值 随角度的增加而减小
5、特殊的三角函数值
例5：计算
Sin 45° – (√3 - 2006 ) + 6 tan30°
2
—-
0
攻略：要求熟记特殊角的三角函数值表
例6：如果√CosA - 0.5 + ∣√3 tanB - 3∣= 0，那么△ABC是（ ） A、锐角 B、直角 C、等腰 D、钝角
————————---
——
B
例7、已知如图，在△ABC中∠B = 45°, ∠C = 60°，AB = 8 ，求AC的长。
A
B
C
D
6、本课小结：
锐角三角函数的定义和特殊角的三角函数值。
7、作业：指导丛书