相似三角形的性质和判定第2课时

(共13张PPT)
相似三角形的性质和判定
第 2 课 时
桥头河镇株木中学 谢彦文
◆ 全等三角形是怎样定义的？我们判定两个三角形全等的时候，发现定义的条件减少一些的时候，同样也可以判别三角形全等。那么一共有哪些判定的方法呢？
边边边、角边角、角角边、角边角。
◆ 相似三角形的判定定理1，类似于全等三角形判定的哪个方法？其条件是怎样改变的？从全等三角形的判定ASA，AAS中，你能通过类比、猜想得到相似的判定方法吗？它是真命题还是假命题？
两角对应相等。因为一边是无法成比例的。
画△ABC，使∠A=30°， ∠B=45° ，再画△A′B′C′ ，使∠A′=30°， ∠B′=45° 。观察这两个三角形形状相同吗？你能证明∠C= ∠C′吗？量出两个三角形的三边，计算对应边是否对应成比例？由此你可以得出什么结论？
判定定理2：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。
即：两角对应相等的两个三角形相似。
等边三角形都相似吗？
等腰三角形都相似吗？
有一个角对应相等的两个直角三角形相似吗？
有一个锐角相等的两个直角三角形相似吗？
在△ABC与△DEF中，∠A=48°， ∠ B=82 °， ∠D=48 ° ，∠F=50 °， △ABC~△DEF吗？为什么？
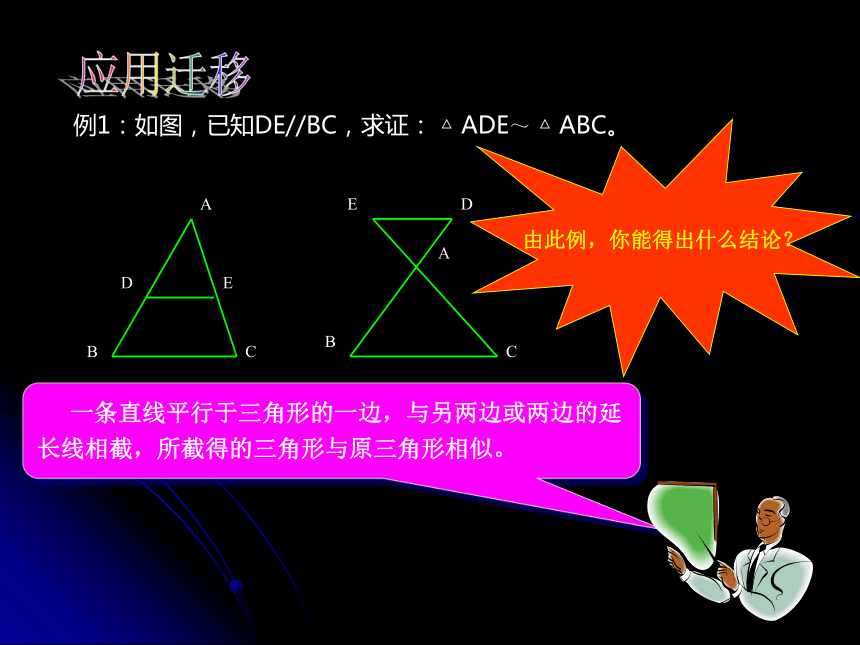
例1：如图，已知DE//BC，求证： △ ADE～ △ ABC。
A
E
D
C
B
A
E
D
C
B
一条直线平行于三角形的一边，与另两边或两边的延长线相截，所截得的三角形与原三角形相似。
由此例，你能得出什么结论？
例2：如图，已知△ABC中，D，E分别是AC，AB上的点，且∠AED= ∠ C，求证： △ADE ～ △ABC。
A
E
D
C
B
提示：有关相似三角形的判定中，公共角或对顶角是题中的隐含条件，都是对应角。
证明：在△ADE 与 △ABC中，
∵ ∠AED= ∠ C（已知）
∠A= ∠ A（公共角）
∴ △ADE ～ △ABC（有两个角对应相等的三角形相似）
例3：如图，已知，△ABC～ △A ' B ' C ' ，相似比为k，AD、A ' D'分别是BC、B ' C '上的高，求证：AD:A ' D ' =k
A
C
D
B
A
C
D
B
提示：要证AD:A ' D ' =k联想到△ABC～ △A ' B ' C '可证AB:A ' B ' =AC:A ' C ' =BC:B ' C ' =k ，故只需要证明AD:A ' D ' =AB:A ' B ' 或者AD:A ' D ' =AC:A ' C '或者AD:A ' D ' =BC:B ' C '，要证对应边成比例的基本方法之一就是寻找四条线段所在的两个三角形是否相似。
还有别的思路吗？
思路2：由高联想到面积
例3：如图，已知，△ABC～ △A ' B ' C ' ，相似比为k，AD、A ' D'分别是BC、B ' C '上的高，求证：AD:A ' D ' =k
A
C
D
B
A
C
D
B
（1）由此例，你能得出什么结论？
相似三角形对应边上的高之比等于相似比。
相似三角形的面积之比等于相似比的平方。
（1）相似三角形的面积之比等于对应高的比吗？为什么？
（2）相似三角形的相似比等于面积之比的算术平方根吗？
1. △ABC～ △A ‘B ’ C ‘，△ABC中最长的边为15， △A ’ B ‘ C ’ 中最长的边为5，则下列判断错误的是 ( )
A. 相似比为3：1 B. 对应边上的高之比为1：3
C. 面积之比为9：1 D. 周长之比为3：1
2. 两相似三角形的面积之比为9：25，则对应边上的高之比为＿ ＿ ＿ ＿
3. 一个三角形各边之比为2：5：6，和它相似的另一个三角形的最小边为6，则它的最长边为＿ ＿ ＿
B
3：5
18
4.如图，要使△ACD～△BCA，下列各式中必须成立的是（ ）
A
D
C
B
A. AC/CD=AB/BC B. CD/AD=BC/AB
C. CD =AD·DB D. AC =CD·CB
D
通过本堂课的学习，你有哪些收获？还有什么困惑吗？
一、必做题：
1。在△ABC与△DEF中，∠A=39 ° ， ∠B =61 ° ， ∠E=39 ° ， ∠F=80° ，则△▁▁▁▁～ △ABC。
2。已知如图1，在△ABC中， D是AB边上的点，且∠ ACD=∠B，求证： △ACD～ △ABC
3。求证：相似三角形对应角的角平分线之比等于相似比。
二、选做题：
如图2， △ABC中， ∠C=90 ° ，CD⊥AB，垂足为D，
（1）写出图中的相似三角形；
（2）求证： CD =AD·DB， AC =AD·AB， BC =BD·AB
∟
∟
A
C
D
C
B
A
D
B
图1
图2