六年级上册数学课件-8 数学广角——数与形 人教版(共17张PPT)
文档属性
| 名称 | 六年级上册数学课件-8 数学广角——数与形 人教版(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 06:22:51 | ||
图片预览





文档简介
8 数学广角——数与形
1+3+5+7+9 =
小组合作:
利用手中的小正方形摆1+3(摆成一个图形)并思考:怎样摆更有利于解决这个问题?
(注意:先摆一摆,确定好摆的图形后,把它粘在题单上)
2. 利用手中的小正方形摆1+3+5(摆成一个图形)并用算式表示出小正方形的个数。
{F5AB1C69-6EDB-4FF4-983F-18BD219EF322}
1+3+5+7 =
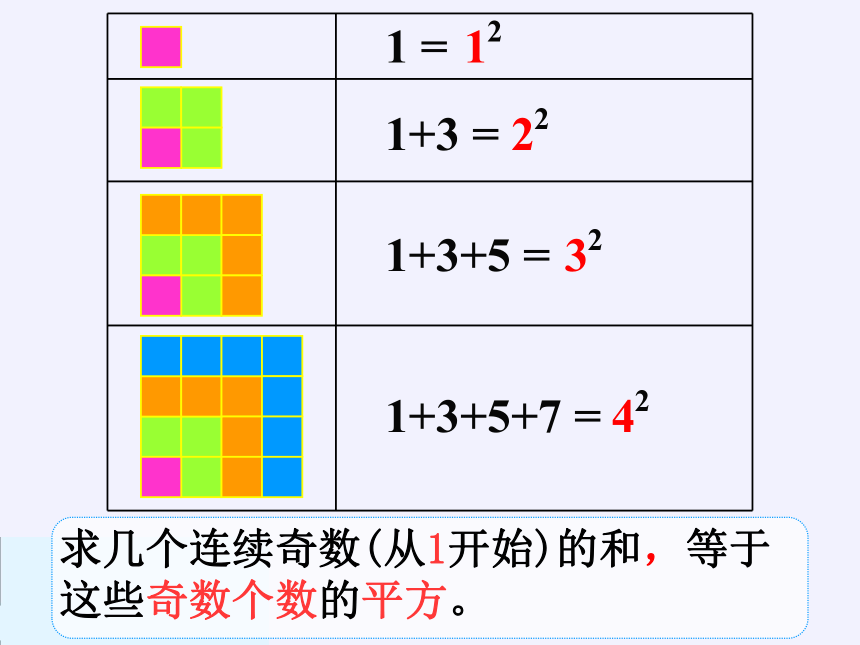
1+3 =
1+3+5 =
1 =
1
2
2
2
3
2
4
2
求几个连续奇数(从1开始)的和,等于这些奇数个数的平方。
1+3+5+7+9+11+13 =
7
2
_______________________=
1+3+5+7+9+11+13+15+17
9
2
7个
=49
1+3+5+7+9+11+13 +15=
8
2
8个
=64
1+3+5+7+ … +39 =
20
2
20个
=400
1+3+5+7+9+11+13+11+9+7+5+3+1
=( )
想:
请你根据刚才的结论算一算。
桌子数:
人数:
3
1
4
2
6
8
想一想:10张桌子能坐几个人?
你能用一个关系式表示桌子数和人数间的关系吗?
10 × 2 + 2 = 22
桌子数
人数
×2+2=
(个)
10 × 2 + 2 = 22
在以前的学习中,哪些知识用到了数形结合的思想?
数的认识
数的运算
解决问题
统计图
确定位置
数缺形时少直观,
数形结合百般好,
华罗庚
学习了这节课,你有什么收获?
形缺数时难入微。
隔离分家万事休。
谢 谢
1+3+5+7+9 =
小组合作:
利用手中的小正方形摆1+3(摆成一个图形)并思考:怎样摆更有利于解决这个问题?
(注意:先摆一摆,确定好摆的图形后,把它粘在题单上)
2. 利用手中的小正方形摆1+3+5(摆成一个图形)并用算式表示出小正方形的个数。
{F5AB1C69-6EDB-4FF4-983F-18BD219EF322}
1+3+5+7 =
1+3 =
1+3+5 =
1 =
1
2
2
2
3
2
4
2
求几个连续奇数(从1开始)的和,等于这些奇数个数的平方。
1+3+5+7+9+11+13 =
7
2
_______________________=
1+3+5+7+9+11+13+15+17
9
2
7个
=49
1+3+5+7+9+11+13 +15=
8
2
8个
=64
1+3+5+7+ … +39 =
20
2
20个
=400
1+3+5+7+9+11+13+11+9+7+5+3+1
=( )
想:
请你根据刚才的结论算一算。
桌子数:
人数:
3
1
4
2
6
8
想一想:10张桌子能坐几个人?
你能用一个关系式表示桌子数和人数间的关系吗?
10 × 2 + 2 = 22
桌子数
人数
×2+2=
(个)
10 × 2 + 2 = 22
在以前的学习中,哪些知识用到了数形结合的思想?
数的认识
数的运算
解决问题
统计图
确定位置
数缺形时少直观,
数形结合百般好,
华罗庚
学习了这节课,你有什么收获?
形缺数时难入微。
隔离分家万事休。
谢 谢
