人教版九年级上册24.1.1与圆有关的概念同步练习题(word解析版)
文档属性
| 名称 | 人教版九年级上册24.1.1与圆有关的概念同步练习题(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 62.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-26 00:00:00 | ||
图片预览



文档简介
24.1.1
与圆有关的概念同步练习题
学校:__________
班级:__________
姓名:__________
考号:__________
一、
选择题
(本题共计
15
小题
,每题
4
分
,共计60分
)
?
1.
下列说法正确的是(
)
A.直径是弦,弦是直径
B.过圆心的线段是直径
C.圆中最长的弦是直径
D.直径只有二条
2.
下列说法正确的是(
)
A.直径是弦
B.弧是半圆
C.长度相等的弧是等弧
D.弦是圆上两点间的部分
?
3.
以点为圆心,以为半径画圆,则圆与轴交点坐标为(
)
A.,
B.,
C.,
D.,
?
4.
下列说法,正确的是(
)
A.半径相等的两个圆大小相等
B.长度相等的两条弧是等弧
C.直径不一定是圆中最长的弦
D.圆上两点之间的部分叫做弦
5.
某校计划在校园内修建一座周长为米的花坛,同学们设计出正三角形、正方形和圆共三种图案,其中使花坛面积最大的图案是(
)
A.正三角形
B.正方形
C.圆
D.不能确定
6.
下列条件中,能确定圆的是(
)
A.以点为圆心
B.以长为半径
C.以点为圆心,以长为半径
D.经过已知点
7.
下列说法:
①优弧一定比劣弧长;②面积相等的两个圆是等圆;
③长度相等的弧是等弧;④经过圆心的一个定点可以作无数条弦;
⑤经过圆内一定点可以作无数条直径.
其中不正确的个数是(
)
A.个
B.个
C.个
D.个
?
8.
下列结论正确的是(
)
A.经过圆心的直线是圆的对称轴
B.直径是圆的对称轴
C.与圆相交的直线是圆的对称轴
D.与直径相交的直线是圆的对称轴
9.
下列语句中,不正确的是(
)
A.圆既是中心对称图形,又是旋转对称图形
B.圆是轴对称图形,过圆心的直线是它的对称轴
C.当圆绕它的中心旋转时,不会与原来的圆重合
D.圆的对称轴有无数条,但是对称中心只有一个
10.
下列各图形中,各个顶点一定在同一个圆上的是(
)
A.正方形
B.菱形
C.平行四边形
D.梯形
11.
下列说法正确的是(
)
A.直径是弦,弦是直径
B.半圆是弧
C.无论过圆内哪一点,只能作一条直径
D.直径的长度是半径的倍
12.
下列命题是真命题的个数是(
)
①直径所对的角是;②三点确定一个圆;③圆的切线垂直于过切线的半径;④相等的弦所对的圆周角相等;⑤三角形的内心是三角平分线交点;⑥三角形外心到三角形三个顶点距离相等;
A.个
B.个
C.个
D.个
13.
下列命题中,正确的是个数是(
)
①半圆是弧;②弧是半圆;③直径是弦;④弧长相等的弧是等弧;⑤直径的两个端点分圆所成的两条弧,每一条弧都是半圆.
A.个
B.个
C.个
D.个
14.
圆内最大的弦长为,则圆的半径(
)
A.小于
B.大于
C.等于
D.不能确定
15.
在以下所给的命题中,正确的个数为(
)
①直径是弦;②弦是直径;③半圆是弧,但弧不一定是半圆;④半径相等的两个半圆是等弧;⑤长度相等的弧是等弧.
A.
B.
C.
D.
二、
填空题
(本题共计
15
小题
,每题
4
分
,共计60分)
16.
连接圆上任意两点的________叫做弦,经过________的弦叫做直径.
17.
平面上到________的距离等于________的所有点组成的图形叫做圆,其中,________为圆心,________为半径.
18.
圆是轴对称图形,它有________条对称轴,是________直线;圆还是中心对称图形,对称中心是________
19.
在同一平面内与已知点的距离等于的所有点组成的图形是________.
20.
确定一个圆有两要素,一是________,二是________.
21.
设圆的半径为,面积为,则圆的面积为________.
22.
设圆的半径为,直径为,周长为,则圆的周长为________.
23.
圆上________的部分叫做圆弧,简称弧;________半圆的弧叫做优弧,________半圆的弧叫做劣弧.
24.
以为半径可以画________个圆;以点为圆心可以画________个圆;以点为圆心,以为半径可以画________个圆.
25.
圆既是轴对称图形,又是________对称图形,它的对称轴是________,对称中心是________.
?
26.
如图,在中,半径有________,直径有________,弦有________,劣弧有________,优弧有________.
?
27.
如图,三个同心圆,为圆心,,最大圆的半径为,则图中阴影部分的面积为________(结果保留).
?
28.
菱形四边的中点到________的距离相等,因此菱形各边的中点在以________为圆心,以________为半径的圆上.
?
29.
一点到圆的最小距离为,最大距离为,则此圆的半径是________.
?
30.
经过圆内一点可作圆的________条弦,其中最大的弦是________.
三、
解答题
(本题共计
2
小题
,每题
15
分
,共计30分
)
?
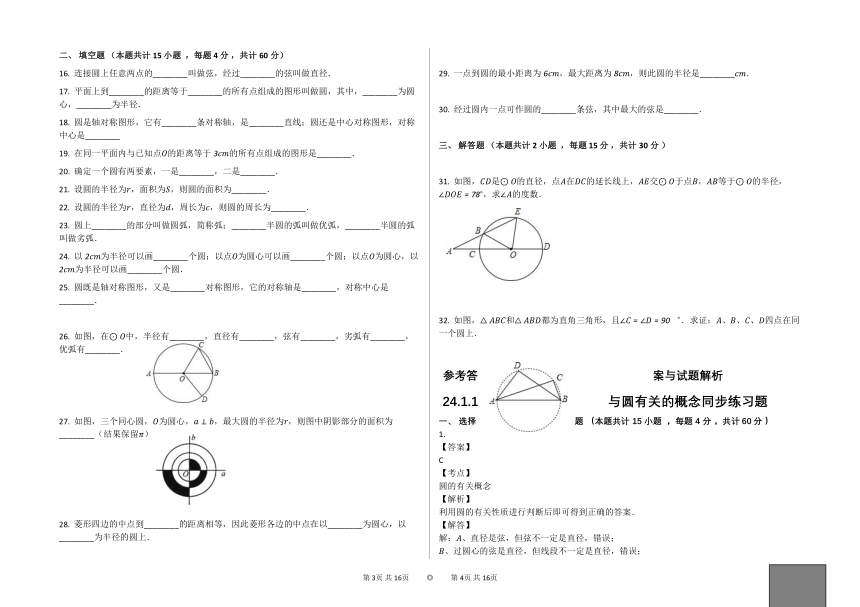
31.
如图,是的直径,点在的延长线上,交于点,等于的半径,,求的度数.
?
32.
如图,和都为直角三角形,且゜.求证:、、、四点在同一个圆上.
参考答案与试题解析
24.1.1与圆有关的概念同步练习题
一、
选择题
(本题共计
15
小题
,每题
4
分
,共计60分
)
1.
【答案】
C
【考点】
圆的有关概念
【解析】
利用圆的有关性质进行判断后即可得到正确的答案.
【解答】
解:、直径是弦,但弦不一定是直径,错误;
、过圆心的弦是直径,但线段不一定是直径,错误;
、圆中最长的弦是直径,正确;
、直径有无数条,错误,
故选.
2.
【答案】
A
【考点】
圆的有关概念
【解析】
根据圆中的有关定义解答即可;
【解答】
解:、直径是弦,是最长的弦,故正确;
、弧分为优弧、劣弧和半圆三种情况,故错误;
、能完全重合的弧是等弧,故错误;
、弧是圆上两点间的部分,故错误,
故选.
3.
【答案】
B
【考点】
坐标与图形性质
圆的有关概念
【解析】
与轴交点的纵坐标都为,在圆上的点到圆的距离等于半径.横坐标为,或.
【解答】
解:因为圆心在轴上,与轴相交两点,
∴
两点的纵坐标都为,
∵
圆的半径是,
∴
两点的横坐标为,或.
即两点的坐标为、.
故选.
4.
【答案】
A
【考点】
圆的有关概念
【解析】
根据弧的定义、等弧的定义即可解决.
【解答】
解:、根据半径确定圆的大小,故正确;
、根据等弧的概念,长度相等的两条弧不一定能够重合,故错误;
、根据三角形的两边之和大于第三边,可以证明直径是圆中最长的弦,故错误;
、圆上任意两点间的部分叫弧,故错误.
故选.
5.
【答案】
C
【考点】
圆的有关概念
【解析】
根据周长分别求得正三角形,正方形,圆的面积,从而比较可得到面积最大的是什么形状.
【解答】
当设计成正三角形,则边长是米,则面积是平方米;
当设计成正方形时,边长是米,则面积是平方米;
当设计成圆时,半径是米,则面积是平方米.
∵
这三个数中最大,
∴
使花坛面积最大的图案是圆.
6.
【答案】
C
【考点】
圆的有关概念
【解析】
根据圆的定义对各选项进行判断.
【解答】
解:、点为圆心,半径不确定,则不能确定圆;
、长为半径,圆心不确定,则不能确定圆;
、以点为圆心,以长为半径可确定圆;
、经过点,则圆心和半径都不能确定,则不能确定圆.
故选.
7.
【答案】
B
【考点】
圆的有关概念
【解析】
根据劣弧与优弧的定义对①进行判断;根据等圆的定义对②进行判断;根据等弧的定义对③进行判断;根据弦的定义对④进行判断;根据定点是否为圆心可对⑤进行判断.
【解答】
解:在同圆或等圆中,优弧一定比劣弧长,所以①错误;
面积相等的两个圆半径相等,则它们是等圆,所以②正确;
能完全重合的弧是等弧,所以③错误;
经过圆内一个定点可以作无数条弦,所以④正确;
经过圆内一定点可以作无数条直径或一条直径,所以⑤错误.
故选.
8.
【答案】
A
【考点】
圆的有关概念
【解析】
利用直径所在的直线为圆的对称轴对各选项进行判断.
【解答】
解:、经过圆心的直线是圆的对称轴,所以正确;
、直径所在的直线为圆的对称轴,所以错误;
、与圆相交的直线不一定是圆的对称轴,所以错误;
、与直径相交的圆心的直线是圆的对称轴,所以错误.
故选.
9.
【答案】
C
【考点】
圆的有关概念
【解析】
根据圆既是中心对称图形,又是旋转对称图形可对各选项进行判断.
【解答】
解:、圆既是中心对称图形,又是旋转对称图形,所以选项的说法正确;
、圆是轴对称图形,过圆心的直线是它的对称轴,所以选项的说法正确;
、当圆绕它的中心旋转时,会与原来的圆重合,所以选项的说法不正确;
、圆的对称轴有无数条,但是对称中心只有一个,即为圆心,所以选项的说法正确.
故选.
10.
【答案】
A
【考点】
圆的有关概念
【解析】
四个顶点可在同一个圆上的四边形,一定有一点到它的四个顶点的距离都相等,因而、、都是错误的;正方形的四个顶点到对角线的交点的距离都相同,因而正方形的四个顶点一定可以在同一个圆上.
【解答】
解:∵
正方形对角线相等且互相平分,
∴
四个顶点到对角线交点距离相等,
∴
正方形四个顶点定可在同一个圆上.
故选:.
11.
【答案】
B
【考点】
圆的有关概念
【解析】
根据圆的有关知识进行分析,从而得到答案.
【解答】
解:、直径是圆中特殊的弦,但弦不一定是直径,所以错误;
、半圆是特殊的弧,故正确;
、过圆内的点圆心有无数条直径,故错误;
、直径的长度是同一个圆的半径的倍,故错误.
故选.
12.
【答案】
A
【考点】
确定圆的条件
圆的有关概念
垂径定理
三角形的外接圆与外心
【解析】
根据与圆有关的知识及性质定理,作出准确的判断,①直径所对的圆周角是;②缺少条件,不在同一直线上的三个点才能确定一个圆;③圆的切线垂直于过切点的半径,而不是过切线的半径;④相等的弦所对的圆周角也可能互补,因为一条弦对着两个圆周角;⑤⑥是正确的.
【解答】
解:①直径所对的圆周角的度数是,直径所对其他的角的度数不一定是直角;故错误.
②过不在同一直线上的三点确定一个圆,过同一直线上的三点不能确定圆;故错误.
③根据切线的性质定理,圆的切线垂直于过切点的半径;故错误.
④相等的弦所对的圆周角也可能互补,因为一条弦对着两个圆周角;故错误.
⑤三角形的内心到三角形的三边的距离相等,是三角形角平分线的交点;故正确.
⑥三角形外心是三角形三边垂直平分线的交点,到三角形三个顶点距离相等;故正确.
故选.
13.
【答案】
C
【考点】
命题与定理
圆的有关概念
【解析】
利用圆的有关定义及性质分别判断后即可确定正确的选项.
【解答】
解:①半圆是弧,正确;
②弧是半圆,错误;
③直径是弦,正确;
④弧长相等的弧是等弧,错误;
⑤直径的两个端点分圆所成的两条弧,每一条弧都是半圆,正确,
正确的有三个,
故选.
14.
【答案】
C
【考点】
圆的有关概念
【解析】
根据直径是圆中最长的弦,可以得到圆的直径是,再由直径是半径的两倍求出半径.
【解答】
解:因为直径是圆中最长的弦,而圆的最长弦长为,
所以直径是,半径是.
故选.
15.
【答案】
C
【考点】
圆的有关概念
【解析】
根据弦的定义、弧的定义、以及等弧的定义即可解决.
【解答】
解:根据直径和弦的概念,知①正确,②错误;
根据弧和半圆的概念,知③正确;
根据等弧的概念,半径相等的两个半圆一定能够重合,是等弧,④正确;
长度相等的两条弧不一定能够重合,⑤错误.
故选.
二、
填空题
(本题共计
15
小题
,每题
4
分
,共计60分
)
16.
【答案】
线段,圆心
【考点】
圆的有关概念
【解析】
根据:连接圆上任意两点的线段叫弦,经过圆心的弦叫直径,直径是最长的弦,从而可填空.
【解答】
解:连接任意两点的线段叫做弦.经过圆心的弦叫做直径.
故答案为:线段;圆心;
17.
【答案】
定点,定长,定点,定长
【考点】
圆的有关概念
【解析】
利用圆的集合定义直接回答即可.
【解答】
解:平面上到定点的距离等于定长的所有点组成的图形叫做圆,其中,定点为圆心,定长为半径.
故答案为:定点,定长,定点,定长.
18.
【答案】
无数,过圆心的或直径所在的,圆心
【考点】
圆的有关概念
【解析】
圆是一种比较特殊的几何图形,圆既是轴对称图形,又是中心对称图形,具有旋转不变性,有无数条对称轴.
【解答】
解:圆是轴对称图形,圆有无数条对称轴,任何过圆心的直线都是圆的对称轴,或者说任何直径所在的直线都是圆的对称轴,圆也是中心对称图形,圆心是其对称中心,圆具有旋转不变性.
故答案为:无数;过圆心的或直径所在的;圆心.
19.
【答案】
以点为圆心,长为半径的圆
【考点】
圆的有关概念
【解析】
到顶点的距离等于定长的所有点组成的图形就是以顶点为圆心,以定长为半径的圆.
【解答】
解:到点的距离等于的所有点组成的图形是:以点为圆心,长为半径的圆.
故答案为:以点为圆心,长为半径的圆.
20.
【答案】
圆心,半径
【考点】
圆的有关概念
认识平面图形
【解析】
根据圆的定义:在一个平面内,线段绕固定的端点旋转一周,另一个端点所形成的图形就是圆.可以知道确定一个圆的两个要素.
【解答】
解:由圆的定义有:固定的端点是圆心,线段是半径,
所以确定一个圆的两个要素是圆心和半径.
故答案分别是:圆心,半径.
21.
【答案】
【考点】
圆的有关概念
【解析】
根据圆的面积公式求解.
【解答】
解:.
故答案为.
22.
【答案】
或.
【考点】
圆的有关概念
【解析】
根据圆的周长的定义求解.
【解答】
解:圆的周长或.
故答案为或.
23.
【答案】
任意两点间,大于,小于
【考点】
圆的有关概念
【解析】
根据弧、劣弧和优弧的概念求解.
【解答】
解:圆上任意两点间的部分叫做圆弧,简称弧;
大于半圆的弧叫做优弧;
小于半圆的弧叫做劣弧.
故答案为:任意两点间;大于;小于.
24.
【答案】
无数,无数,一
【考点】
圆的有关概念
【解析】
根据圆的定义求解.
【解答】
解:以为半径可以画无数个圆;以点为圆心可以画无数个圆;以点为圆心,以为半径可以画一个圆.
故答案为:无数;无数;一.
25.
【答案】
中心,过圆心的任一条直线,圆心
【考点】
圆的有关概念
【解析】
根据圆的知识填空即可.
【解答】
解:圆既是轴对称图形,又是中心对称图形,它的对称轴是过圆心的任一条直径,对称中心是圆心.
26.
【答案】
、、、,,、,、、、、,、、、、
【考点】
圆的有关概念
【解析】
根据半径、直径、弦、劣弧和优弧的定义求解.
【解答】
解:在中,半径有、、、,直径有,弦有、,劣弧有、、、、,优弧有、、、、.
故答案为、、、;、;、、、、;、、、、.
27.
【答案】
【考点】
轴对称的性质
圆的有关概念
【解析】
结合图形发现:每个阴影部分正好是它所在的圆的四分之一,则阴影部分的面积是大圆面积的.
【解答】
解:∵
大圆面积,∴
阴影部分面积.
28.
【答案】
对角线的交点,对角线的交点,四边中点到对角线交点距离
【考点】
圆的有关概念
菱形的性质
【解析】
根据菱形对角线互相垂直且互相平分,可以得到四个全等的直角三角形,由直角三角形斜边上的中线等于斜边的一半,可以得到四个直角三角形斜边上的中线都相等,然后由圆的定义得到到定点的距离等于定长的点在以定点为圆心定长为半径的圆上.
【解答】
解:因为菱形的对角线互相垂直且互相平分,
所以连接两条对角线,得到四个全等的直角三角形,
又因为直角三角形斜边上的中线等于斜边的一半,
所以四个直角三角形斜边上的中线都相等.
故菱形四边的中点到对角线的交点的距离相等.
菱形各边的中点在以对角线的交点为圆心,以四边中点到对角线交点距离为半径的圆上.
故答案分别是:对角线的交点,对角线的交点,四边中点到对角线交点距离.
29.
【答案】
或
【考点】
点与圆的位置关系
圆的有关概念
【解析】
当点在圆内时,最大距离与最小距离的和等于圆的直径;当点在圆外时,最大距离与最小距离的差等于直径.然后确定圆的半径.
【解答】
解:当点在圆内时,圆的直径是,所以半径是.
当点在圆外时,圆的直径时,所以半径是.
故答案是:或.
30.
【答案】
无数,直径
【考点】
圆的有关概念
【解析】
根据连接圆上任意两点间的线段是直径,则圆中有无数条弦;根据两边之和大于第三边,可以证明圆中最长的弦是直径.
【解答】
解:经过圆内一点可作圆的无数条弦,其中最大的弦是直径.
三、
解答题
(本题共计
2
小题
,每题
15
分
,共计30分
)
31.
【答案】
解:∵
等于的半径,
∴
,
∴
,
∵
,
∴
,
∵
,
∴
,
∵
,
∴
,
∴
.
【考点】
圆的有关概念
等腰三角形的判定与性质
【解析】
根据等腰三角形的性质,由得到,由得到,再根据三角形外角性质得到,则,然后利用得到.
【解答】
解:∵
等于的半径,
∴
,
∴
,
∵
,
∴
,
∵
,
∴
,
∵
,
∴
,
∴
.
32.
【答案】
证明:取的中点,连接,,
∵
和都为直角三角形,且゜
∴
,分别为和斜边上的中线,
∴
.
∴
、、、四点在同一个圆上.
【考点】
圆的有关概念
直角三角形斜边上的中线
【解析】
取的中点,利用直角三角形斜边上的中线等于斜边的一半证得后即可求证、、、四点在同一个圆上.
【解答】
证明:取的中点,连接,,
∵
和都为直角三角形,且゜
∴
,分别为和斜边上的中线,
∴
.
∴
、、、四点在同一个圆上.
第7页
共20页
◎
第8页
共20页
第9页
共20页
◎
第10页
共20页
与圆有关的概念同步练习题
学校:__________
班级:__________
姓名:__________
考号:__________
一、
选择题
(本题共计
15
小题
,每题
4
分
,共计60分
)
?
1.
下列说法正确的是(
)
A.直径是弦,弦是直径
B.过圆心的线段是直径
C.圆中最长的弦是直径
D.直径只有二条
2.
下列说法正确的是(
)
A.直径是弦
B.弧是半圆
C.长度相等的弧是等弧
D.弦是圆上两点间的部分
?
3.
以点为圆心,以为半径画圆,则圆与轴交点坐标为(
)
A.,
B.,
C.,
D.,
?
4.
下列说法,正确的是(
)
A.半径相等的两个圆大小相等
B.长度相等的两条弧是等弧
C.直径不一定是圆中最长的弦
D.圆上两点之间的部分叫做弦
5.
某校计划在校园内修建一座周长为米的花坛,同学们设计出正三角形、正方形和圆共三种图案,其中使花坛面积最大的图案是(
)
A.正三角形
B.正方形
C.圆
D.不能确定
6.
下列条件中,能确定圆的是(
)
A.以点为圆心
B.以长为半径
C.以点为圆心,以长为半径
D.经过已知点
7.
下列说法:
①优弧一定比劣弧长;②面积相等的两个圆是等圆;
③长度相等的弧是等弧;④经过圆心的一个定点可以作无数条弦;
⑤经过圆内一定点可以作无数条直径.
其中不正确的个数是(
)
A.个
B.个
C.个
D.个
?
8.
下列结论正确的是(
)
A.经过圆心的直线是圆的对称轴
B.直径是圆的对称轴
C.与圆相交的直线是圆的对称轴
D.与直径相交的直线是圆的对称轴
9.
下列语句中,不正确的是(
)
A.圆既是中心对称图形,又是旋转对称图形
B.圆是轴对称图形,过圆心的直线是它的对称轴
C.当圆绕它的中心旋转时,不会与原来的圆重合
D.圆的对称轴有无数条,但是对称中心只有一个
10.
下列各图形中,各个顶点一定在同一个圆上的是(
)
A.正方形
B.菱形
C.平行四边形
D.梯形
11.
下列说法正确的是(
)
A.直径是弦,弦是直径
B.半圆是弧
C.无论过圆内哪一点,只能作一条直径
D.直径的长度是半径的倍
12.
下列命题是真命题的个数是(
)
①直径所对的角是;②三点确定一个圆;③圆的切线垂直于过切线的半径;④相等的弦所对的圆周角相等;⑤三角形的内心是三角平分线交点;⑥三角形外心到三角形三个顶点距离相等;
A.个
B.个
C.个
D.个
13.
下列命题中,正确的是个数是(
)
①半圆是弧;②弧是半圆;③直径是弦;④弧长相等的弧是等弧;⑤直径的两个端点分圆所成的两条弧,每一条弧都是半圆.
A.个
B.个
C.个
D.个
14.
圆内最大的弦长为,则圆的半径(
)
A.小于
B.大于
C.等于
D.不能确定
15.
在以下所给的命题中,正确的个数为(
)
①直径是弦;②弦是直径;③半圆是弧,但弧不一定是半圆;④半径相等的两个半圆是等弧;⑤长度相等的弧是等弧.
A.
B.
C.
D.
二、
填空题
(本题共计
15
小题
,每题
4
分
,共计60分)
16.
连接圆上任意两点的________叫做弦,经过________的弦叫做直径.
17.
平面上到________的距离等于________的所有点组成的图形叫做圆,其中,________为圆心,________为半径.
18.
圆是轴对称图形,它有________条对称轴,是________直线;圆还是中心对称图形,对称中心是________
19.
在同一平面内与已知点的距离等于的所有点组成的图形是________.
20.
确定一个圆有两要素,一是________,二是________.
21.
设圆的半径为,面积为,则圆的面积为________.
22.
设圆的半径为,直径为,周长为,则圆的周长为________.
23.
圆上________的部分叫做圆弧,简称弧;________半圆的弧叫做优弧,________半圆的弧叫做劣弧.
24.
以为半径可以画________个圆;以点为圆心可以画________个圆;以点为圆心,以为半径可以画________个圆.
25.
圆既是轴对称图形,又是________对称图形,它的对称轴是________,对称中心是________.
?
26.
如图,在中,半径有________,直径有________,弦有________,劣弧有________,优弧有________.
?
27.
如图,三个同心圆,为圆心,,最大圆的半径为,则图中阴影部分的面积为________(结果保留).
?
28.
菱形四边的中点到________的距离相等,因此菱形各边的中点在以________为圆心,以________为半径的圆上.
?
29.
一点到圆的最小距离为,最大距离为,则此圆的半径是________.
?
30.
经过圆内一点可作圆的________条弦,其中最大的弦是________.
三、
解答题
(本题共计
2
小题
,每题
15
分
,共计30分
)
?
31.
如图,是的直径,点在的延长线上,交于点,等于的半径,,求的度数.
?
32.
如图,和都为直角三角形,且゜.求证:、、、四点在同一个圆上.
参考答案与试题解析
24.1.1与圆有关的概念同步练习题
一、
选择题
(本题共计
15
小题
,每题
4
分
,共计60分
)
1.
【答案】
C
【考点】
圆的有关概念
【解析】
利用圆的有关性质进行判断后即可得到正确的答案.
【解答】
解:、直径是弦,但弦不一定是直径,错误;
、过圆心的弦是直径,但线段不一定是直径,错误;
、圆中最长的弦是直径,正确;
、直径有无数条,错误,
故选.
2.
【答案】
A
【考点】
圆的有关概念
【解析】
根据圆中的有关定义解答即可;
【解答】
解:、直径是弦,是最长的弦,故正确;
、弧分为优弧、劣弧和半圆三种情况,故错误;
、能完全重合的弧是等弧,故错误;
、弧是圆上两点间的部分,故错误,
故选.
3.
【答案】
B
【考点】
坐标与图形性质
圆的有关概念
【解析】
与轴交点的纵坐标都为,在圆上的点到圆的距离等于半径.横坐标为,或.
【解答】
解:因为圆心在轴上,与轴相交两点,
∴
两点的纵坐标都为,
∵
圆的半径是,
∴
两点的横坐标为,或.
即两点的坐标为、.
故选.
4.
【答案】
A
【考点】
圆的有关概念
【解析】
根据弧的定义、等弧的定义即可解决.
【解答】
解:、根据半径确定圆的大小,故正确;
、根据等弧的概念,长度相等的两条弧不一定能够重合,故错误;
、根据三角形的两边之和大于第三边,可以证明直径是圆中最长的弦,故错误;
、圆上任意两点间的部分叫弧,故错误.
故选.
5.
【答案】
C
【考点】
圆的有关概念
【解析】
根据周长分别求得正三角形,正方形,圆的面积,从而比较可得到面积最大的是什么形状.
【解答】
当设计成正三角形,则边长是米,则面积是平方米;
当设计成正方形时,边长是米,则面积是平方米;
当设计成圆时,半径是米,则面积是平方米.
∵
这三个数中最大,
∴
使花坛面积最大的图案是圆.
6.
【答案】
C
【考点】
圆的有关概念
【解析】
根据圆的定义对各选项进行判断.
【解答】
解:、点为圆心,半径不确定,则不能确定圆;
、长为半径,圆心不确定,则不能确定圆;
、以点为圆心,以长为半径可确定圆;
、经过点,则圆心和半径都不能确定,则不能确定圆.
故选.
7.
【答案】
B
【考点】
圆的有关概念
【解析】
根据劣弧与优弧的定义对①进行判断;根据等圆的定义对②进行判断;根据等弧的定义对③进行判断;根据弦的定义对④进行判断;根据定点是否为圆心可对⑤进行判断.
【解答】
解:在同圆或等圆中,优弧一定比劣弧长,所以①错误;
面积相等的两个圆半径相等,则它们是等圆,所以②正确;
能完全重合的弧是等弧,所以③错误;
经过圆内一个定点可以作无数条弦,所以④正确;
经过圆内一定点可以作无数条直径或一条直径,所以⑤错误.
故选.
8.
【答案】
A
【考点】
圆的有关概念
【解析】
利用直径所在的直线为圆的对称轴对各选项进行判断.
【解答】
解:、经过圆心的直线是圆的对称轴,所以正确;
、直径所在的直线为圆的对称轴,所以错误;
、与圆相交的直线不一定是圆的对称轴,所以错误;
、与直径相交的圆心的直线是圆的对称轴,所以错误.
故选.
9.
【答案】
C
【考点】
圆的有关概念
【解析】
根据圆既是中心对称图形,又是旋转对称图形可对各选项进行判断.
【解答】
解:、圆既是中心对称图形,又是旋转对称图形,所以选项的说法正确;
、圆是轴对称图形,过圆心的直线是它的对称轴,所以选项的说法正确;
、当圆绕它的中心旋转时,会与原来的圆重合,所以选项的说法不正确;
、圆的对称轴有无数条,但是对称中心只有一个,即为圆心,所以选项的说法正确.
故选.
10.
【答案】
A
【考点】
圆的有关概念
【解析】
四个顶点可在同一个圆上的四边形,一定有一点到它的四个顶点的距离都相等,因而、、都是错误的;正方形的四个顶点到对角线的交点的距离都相同,因而正方形的四个顶点一定可以在同一个圆上.
【解答】
解:∵
正方形对角线相等且互相平分,
∴
四个顶点到对角线交点距离相等,
∴
正方形四个顶点定可在同一个圆上.
故选:.
11.
【答案】
B
【考点】
圆的有关概念
【解析】
根据圆的有关知识进行分析,从而得到答案.
【解答】
解:、直径是圆中特殊的弦,但弦不一定是直径,所以错误;
、半圆是特殊的弧,故正确;
、过圆内的点圆心有无数条直径,故错误;
、直径的长度是同一个圆的半径的倍,故错误.
故选.
12.
【答案】
A
【考点】
确定圆的条件
圆的有关概念
垂径定理
三角形的外接圆与外心
【解析】
根据与圆有关的知识及性质定理,作出准确的判断,①直径所对的圆周角是;②缺少条件,不在同一直线上的三个点才能确定一个圆;③圆的切线垂直于过切点的半径,而不是过切线的半径;④相等的弦所对的圆周角也可能互补,因为一条弦对着两个圆周角;⑤⑥是正确的.
【解答】
解:①直径所对的圆周角的度数是,直径所对其他的角的度数不一定是直角;故错误.
②过不在同一直线上的三点确定一个圆,过同一直线上的三点不能确定圆;故错误.
③根据切线的性质定理,圆的切线垂直于过切点的半径;故错误.
④相等的弦所对的圆周角也可能互补,因为一条弦对着两个圆周角;故错误.
⑤三角形的内心到三角形的三边的距离相等,是三角形角平分线的交点;故正确.
⑥三角形外心是三角形三边垂直平分线的交点,到三角形三个顶点距离相等;故正确.
故选.
13.
【答案】
C
【考点】
命题与定理
圆的有关概念
【解析】
利用圆的有关定义及性质分别判断后即可确定正确的选项.
【解答】
解:①半圆是弧,正确;
②弧是半圆,错误;
③直径是弦,正确;
④弧长相等的弧是等弧,错误;
⑤直径的两个端点分圆所成的两条弧,每一条弧都是半圆,正确,
正确的有三个,
故选.
14.
【答案】
C
【考点】
圆的有关概念
【解析】
根据直径是圆中最长的弦,可以得到圆的直径是,再由直径是半径的两倍求出半径.
【解答】
解:因为直径是圆中最长的弦,而圆的最长弦长为,
所以直径是,半径是.
故选.
15.
【答案】
C
【考点】
圆的有关概念
【解析】
根据弦的定义、弧的定义、以及等弧的定义即可解决.
【解答】
解:根据直径和弦的概念,知①正确,②错误;
根据弧和半圆的概念,知③正确;
根据等弧的概念,半径相等的两个半圆一定能够重合,是等弧,④正确;
长度相等的两条弧不一定能够重合,⑤错误.
故选.
二、
填空题
(本题共计
15
小题
,每题
4
分
,共计60分
)
16.
【答案】
线段,圆心
【考点】
圆的有关概念
【解析】
根据:连接圆上任意两点的线段叫弦,经过圆心的弦叫直径,直径是最长的弦,从而可填空.
【解答】
解:连接任意两点的线段叫做弦.经过圆心的弦叫做直径.
故答案为:线段;圆心;
17.
【答案】
定点,定长,定点,定长
【考点】
圆的有关概念
【解析】
利用圆的集合定义直接回答即可.
【解答】
解:平面上到定点的距离等于定长的所有点组成的图形叫做圆,其中,定点为圆心,定长为半径.
故答案为:定点,定长,定点,定长.
18.
【答案】
无数,过圆心的或直径所在的,圆心
【考点】
圆的有关概念
【解析】
圆是一种比较特殊的几何图形,圆既是轴对称图形,又是中心对称图形,具有旋转不变性,有无数条对称轴.
【解答】
解:圆是轴对称图形,圆有无数条对称轴,任何过圆心的直线都是圆的对称轴,或者说任何直径所在的直线都是圆的对称轴,圆也是中心对称图形,圆心是其对称中心,圆具有旋转不变性.
故答案为:无数;过圆心的或直径所在的;圆心.
19.
【答案】
以点为圆心,长为半径的圆
【考点】
圆的有关概念
【解析】
到顶点的距离等于定长的所有点组成的图形就是以顶点为圆心,以定长为半径的圆.
【解答】
解:到点的距离等于的所有点组成的图形是:以点为圆心,长为半径的圆.
故答案为:以点为圆心,长为半径的圆.
20.
【答案】
圆心,半径
【考点】
圆的有关概念
认识平面图形
【解析】
根据圆的定义:在一个平面内,线段绕固定的端点旋转一周,另一个端点所形成的图形就是圆.可以知道确定一个圆的两个要素.
【解答】
解:由圆的定义有:固定的端点是圆心,线段是半径,
所以确定一个圆的两个要素是圆心和半径.
故答案分别是:圆心,半径.
21.
【答案】
【考点】
圆的有关概念
【解析】
根据圆的面积公式求解.
【解答】
解:.
故答案为.
22.
【答案】
或.
【考点】
圆的有关概念
【解析】
根据圆的周长的定义求解.
【解答】
解:圆的周长或.
故答案为或.
23.
【答案】
任意两点间,大于,小于
【考点】
圆的有关概念
【解析】
根据弧、劣弧和优弧的概念求解.
【解答】
解:圆上任意两点间的部分叫做圆弧,简称弧;
大于半圆的弧叫做优弧;
小于半圆的弧叫做劣弧.
故答案为:任意两点间;大于;小于.
24.
【答案】
无数,无数,一
【考点】
圆的有关概念
【解析】
根据圆的定义求解.
【解答】
解:以为半径可以画无数个圆;以点为圆心可以画无数个圆;以点为圆心,以为半径可以画一个圆.
故答案为:无数;无数;一.
25.
【答案】
中心,过圆心的任一条直线,圆心
【考点】
圆的有关概念
【解析】
根据圆的知识填空即可.
【解答】
解:圆既是轴对称图形,又是中心对称图形,它的对称轴是过圆心的任一条直径,对称中心是圆心.
26.
【答案】
、、、,,、,、、、、,、、、、
【考点】
圆的有关概念
【解析】
根据半径、直径、弦、劣弧和优弧的定义求解.
【解答】
解:在中,半径有、、、,直径有,弦有、,劣弧有、、、、,优弧有、、、、.
故答案为、、、;、;、、、、;、、、、.
27.
【答案】
【考点】
轴对称的性质
圆的有关概念
【解析】
结合图形发现:每个阴影部分正好是它所在的圆的四分之一,则阴影部分的面积是大圆面积的.
【解答】
解:∵
大圆面积,∴
阴影部分面积.
28.
【答案】
对角线的交点,对角线的交点,四边中点到对角线交点距离
【考点】
圆的有关概念
菱形的性质
【解析】
根据菱形对角线互相垂直且互相平分,可以得到四个全等的直角三角形,由直角三角形斜边上的中线等于斜边的一半,可以得到四个直角三角形斜边上的中线都相等,然后由圆的定义得到到定点的距离等于定长的点在以定点为圆心定长为半径的圆上.
【解答】
解:因为菱形的对角线互相垂直且互相平分,
所以连接两条对角线,得到四个全等的直角三角形,
又因为直角三角形斜边上的中线等于斜边的一半,
所以四个直角三角形斜边上的中线都相等.
故菱形四边的中点到对角线的交点的距离相等.
菱形各边的中点在以对角线的交点为圆心,以四边中点到对角线交点距离为半径的圆上.
故答案分别是:对角线的交点,对角线的交点,四边中点到对角线交点距离.
29.
【答案】
或
【考点】
点与圆的位置关系
圆的有关概念
【解析】
当点在圆内时,最大距离与最小距离的和等于圆的直径;当点在圆外时,最大距离与最小距离的差等于直径.然后确定圆的半径.
【解答】
解:当点在圆内时,圆的直径是,所以半径是.
当点在圆外时,圆的直径时,所以半径是.
故答案是:或.
30.
【答案】
无数,直径
【考点】
圆的有关概念
【解析】
根据连接圆上任意两点间的线段是直径,则圆中有无数条弦;根据两边之和大于第三边,可以证明圆中最长的弦是直径.
【解答】
解:经过圆内一点可作圆的无数条弦,其中最大的弦是直径.
三、
解答题
(本题共计
2
小题
,每题
15
分
,共计30分
)
31.
【答案】
解:∵
等于的半径,
∴
,
∴
,
∵
,
∴
,
∵
,
∴
,
∵
,
∴
,
∴
.
【考点】
圆的有关概念
等腰三角形的判定与性质
【解析】
根据等腰三角形的性质,由得到,由得到,再根据三角形外角性质得到,则,然后利用得到.
【解答】
解:∵
等于的半径,
∴
,
∴
,
∵
,
∴
,
∵
,
∴
,
∵
,
∴
,
∴
.
32.
【答案】
证明:取的中点,连接,,
∵
和都为直角三角形,且゜
∴
,分别为和斜边上的中线,
∴
.
∴
、、、四点在同一个圆上.
【考点】
圆的有关概念
直角三角形斜边上的中线
【解析】
取的中点,利用直角三角形斜边上的中线等于斜边的一半证得后即可求证、、、四点在同一个圆上.
【解答】
证明:取的中点,连接,,
∵
和都为直角三角形,且゜
∴
,分别为和斜边上的中线,
∴
.
∴
、、、四点在同一个圆上.
第7页
共20页
◎
第8页
共20页
第9页
共20页
◎
第10页
共20页
同课章节目录
