3.1.2 验证勾股定理及其计算同步练习(含答案)
文档属性
| 名称 | 3.1.2 验证勾股定理及其计算同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 16:01:18 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第三章 勾股定理
1 探索勾股定理
第2课时 验证勾股定理及其计算
夯实基础
知识点一 验证勾股定理
1.下列选项中,不能用来证明勾股定理的是( )
2.将四块全等的直角三角形纸板分别拼成如图①、图②所示的正方形,请通过由图①到图②的转换,证明勾股定理。
知识点二 勾股定理的应用
3.如图,有一块边长为24米的正方形绿地,在绿地旁边B处有健身器材,由于居住在A处的居民践踏了绿地,小明想在A处树立一个标牌“少走◇米,踏之何忍?”请你计算后帮小明在标牌的“◇”处填上适当的数字,应为( )
A. 3 B. 4 C. 5 D. 6
第3题图 第4题图
4.如图是一个外轮廓为矩形的机器零件平面示意图根据图中的尺寸(单位:mm),计算两圆孔中心A和B的距离为__________ mm.
5.(盐城阜宁县期中)小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多了1 m,当他把绳子的下端拉开5 m后,发现下端刚好接触地面,求旗杆的高。
易错点 考虑问题不全面而漏解(分类讨论思想)
6.在△ABC中,边AB=15,AC=13,高AD=12,则△ABC的周长是( )
A. 42 B. 32 C. 42或32 D. 不能确定
能力提升
7.(泸州中考)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为( )
A. 9 B. 6 C. 4 D. 3
第7题图 第8题图
8.如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于点M,若CM=5,则CE2+CF2等于( )
A. 75 B. 100 C. 120 D. 125
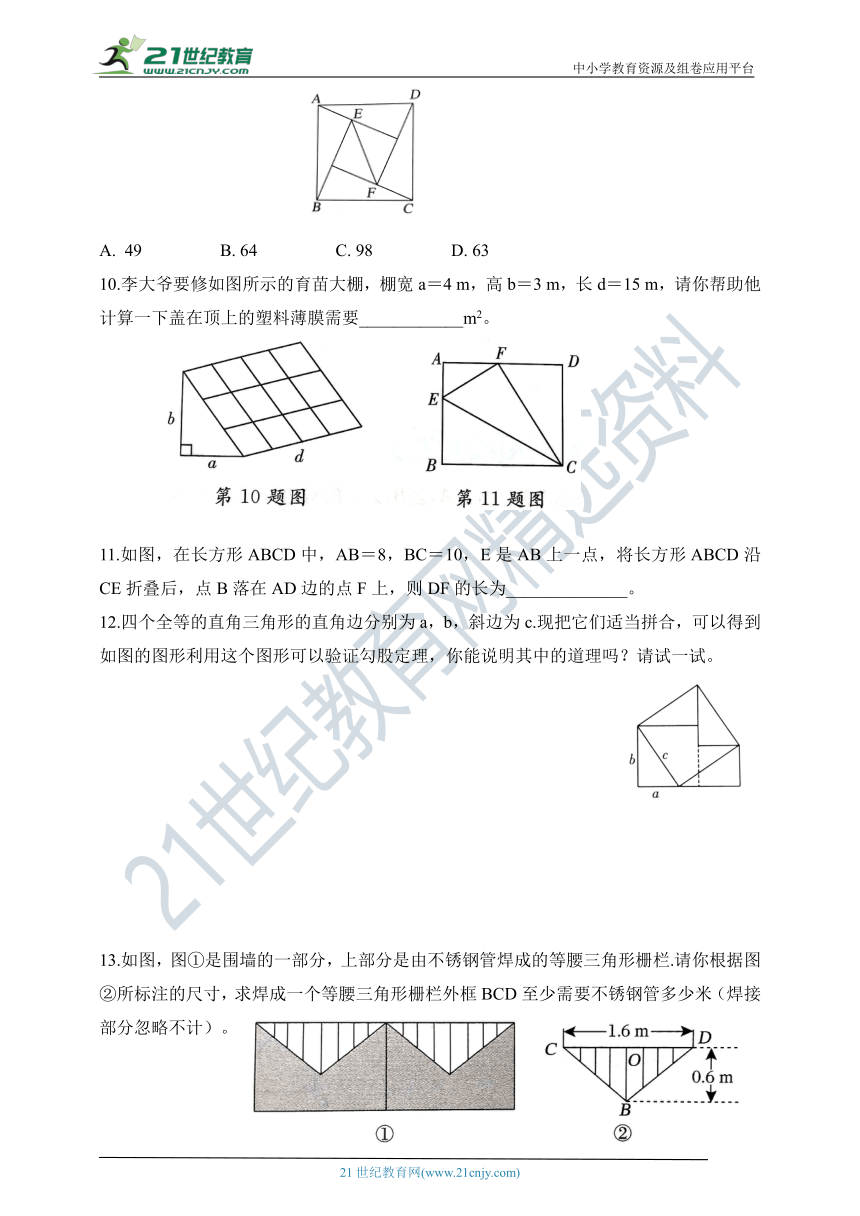
9.已知,如图是由四个全等的直角三角形拼接而成的图形,其中AE=5,BE=12,则EF2是( )
49 B. 64 C. 98 D. 63
10.李大爷要修如图所示的育苗大棚,棚宽a=4 m,高b=3 m,长d=15 m,请你帮助他计算一下盖在顶上的塑料薄膜需要____________m2。
11.如图,在长方形ABCD中,AB=8,BC=10,E是AB上一点,将长方形ABCD沿CE折叠后,点B落在AD边的点F上,则DF的长为______________。
12.四个全等的直角三角形的直角边分别为a,b,斜边为c.现把它们适当拼合,可以得到如图的图形利用这个图形可以验证勾股定理,你能说明其中的道理吗?请试一试。
13.如图,图①是围墙的一部分,上部分是由不锈钢管焊成的等腰三角形栅栏.请你根据图②所标注的尺寸,求焊成一个等腰三角形栅栏外框BCD至少需要不锈钢管多少米(焊接部分忽略不计)。
素养提升
14.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪灵感.他惊喜地发现:当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明.下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连接DB,过点D作BC边上的高DF,DF= EC=b-a.
因为S四边形ADCB=S△ACD+S△ABC=b2+ab,
且S四边形ADCB=S△ADB+S△DCB=c2+a(b-a),所以b2+ab=c2+a(b-a)
所以a2+b2=c2。
请参照上述证法,利用图2完成下面的证明。
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°。
求证:a2+b2=c2。
证明:连接____________________________________________________。
因为S五边形ACBED=____________________________________________,
且S五边形 ACBED=______________________________________________,
所以________________________________________________________。
所以a2+b2=c2。
参考答案
D
解:图①与图②拼出的大正方形面积相等,因此两个大正方形中空白部分的面积相等,
∴c2=b2+a2,即a2+b2=c2。
D
150
解:解:设旗杆的高AB为x m,则绳子AC的长为(x+1)m。
在Rt△ABC中,AB2+BC2=AC2,所以x2+52=(x+1)2,解得x=12.
所以AB=12.故旗杆的高度为12 m。
C 7. D 8. B 9. C
75 11. 6
12.解:图形的总面积可以表示为:c2+2×ab=c2+ab.
也可以表示为:a2+b2+2×ab=a2+b2+ab,所以c2+ab=a2+b2+ab。
所以a2+b2=c2。
13.解:由题意得BO⊥CD.因为△BCD是等腰三角形,所以DO=CD=0.8m.
在Rt△BDO中,因为BD2=DO2+BO2,所以BD==1m,所以BC=1m。
所以等腰三角形栅栏外框BCD至少需要不锈钢管1+1+1.6=3.6m.
14.解:依次填写:
BD,过点B作DE边上的高BF,则BF=b-a。
S△ACB+S△ABE+S△AED=ab+b2+ab
S△ACB+S△ABD+S△BDE=ab+c2+a(b-a)
ab+b2+ab=ab+c2+a(b-a)
_21?????????è?????(www.21cnjy.com)_
第三章 勾股定理
1 探索勾股定理
第2课时 验证勾股定理及其计算
夯实基础
知识点一 验证勾股定理
1.下列选项中,不能用来证明勾股定理的是( )
2.将四块全等的直角三角形纸板分别拼成如图①、图②所示的正方形,请通过由图①到图②的转换,证明勾股定理。
知识点二 勾股定理的应用
3.如图,有一块边长为24米的正方形绿地,在绿地旁边B处有健身器材,由于居住在A处的居民践踏了绿地,小明想在A处树立一个标牌“少走◇米,踏之何忍?”请你计算后帮小明在标牌的“◇”处填上适当的数字,应为( )
A. 3 B. 4 C. 5 D. 6
第3题图 第4题图
4.如图是一个外轮廓为矩形的机器零件平面示意图根据图中的尺寸(单位:mm),计算两圆孔中心A和B的距离为__________ mm.
5.(盐城阜宁县期中)小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多了1 m,当他把绳子的下端拉开5 m后,发现下端刚好接触地面,求旗杆的高。
易错点 考虑问题不全面而漏解(分类讨论思想)
6.在△ABC中,边AB=15,AC=13,高AD=12,则△ABC的周长是( )
A. 42 B. 32 C. 42或32 D. 不能确定
能力提升
7.(泸州中考)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为( )
A. 9 B. 6 C. 4 D. 3
第7题图 第8题图
8.如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于点M,若CM=5,则CE2+CF2等于( )
A. 75 B. 100 C. 120 D. 125
9.已知,如图是由四个全等的直角三角形拼接而成的图形,其中AE=5,BE=12,则EF2是( )
49 B. 64 C. 98 D. 63
10.李大爷要修如图所示的育苗大棚,棚宽a=4 m,高b=3 m,长d=15 m,请你帮助他计算一下盖在顶上的塑料薄膜需要____________m2。
11.如图,在长方形ABCD中,AB=8,BC=10,E是AB上一点,将长方形ABCD沿CE折叠后,点B落在AD边的点F上,则DF的长为______________。
12.四个全等的直角三角形的直角边分别为a,b,斜边为c.现把它们适当拼合,可以得到如图的图形利用这个图形可以验证勾股定理,你能说明其中的道理吗?请试一试。
13.如图,图①是围墙的一部分,上部分是由不锈钢管焊成的等腰三角形栅栏.请你根据图②所标注的尺寸,求焊成一个等腰三角形栅栏外框BCD至少需要不锈钢管多少米(焊接部分忽略不计)。
素养提升
14.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪灵感.他惊喜地发现:当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明.下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连接DB,过点D作BC边上的高DF,DF= EC=b-a.
因为S四边形ADCB=S△ACD+S△ABC=b2+ab,
且S四边形ADCB=S△ADB+S△DCB=c2+a(b-a),所以b2+ab=c2+a(b-a)
所以a2+b2=c2。
请参照上述证法,利用图2完成下面的证明。
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°。
求证:a2+b2=c2。
证明:连接____________________________________________________。
因为S五边形ACBED=____________________________________________,
且S五边形 ACBED=______________________________________________,
所以________________________________________________________。
所以a2+b2=c2。
参考答案
D
解:图①与图②拼出的大正方形面积相等,因此两个大正方形中空白部分的面积相等,
∴c2=b2+a2,即a2+b2=c2。
D
150
解:解:设旗杆的高AB为x m,则绳子AC的长为(x+1)m。
在Rt△ABC中,AB2+BC2=AC2,所以x2+52=(x+1)2,解得x=12.
所以AB=12.故旗杆的高度为12 m。
C 7. D 8. B 9. C
75 11. 6
12.解:图形的总面积可以表示为:c2+2×ab=c2+ab.
也可以表示为:a2+b2+2×ab=a2+b2+ab,所以c2+ab=a2+b2+ab。
所以a2+b2=c2。
13.解:由题意得BO⊥CD.因为△BCD是等腰三角形,所以DO=CD=0.8m.
在Rt△BDO中,因为BD2=DO2+BO2,所以BD==1m,所以BC=1m。
所以等腰三角形栅栏外框BCD至少需要不锈钢管1+1+1.6=3.6m.
14.解:依次填写:
BD,过点B作DE边上的高BF,则BF=b-a。
S△ACB+S△ABE+S△AED=ab+b2+ab
S△ACB+S△ABD+S△BDE=ab+c2+a(b-a)
ab+b2+ab=ab+c2+a(b-a)
_21?????????è?????(www.21cnjy.com)_
