13.3.1等腰三角形第1课时-人教版八年级数学上册课件(19张)
文档属性
| 名称 | 13.3.1等腰三角形第1课时-人教版八年级数学上册课件(19张) |  | |
| 格式 | pptx | ||
| 文件大小 | 613.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-28 10:33:05 | ||
图片预览




文档简介
第十三章 轴对称
13.3 等腰三角形
13.3.1 等腰三角形
第1课时 等腰三角形的性质
温故知新
1、三角形高、角平分线、中线的定义
2、全等三角形的判定
3、角平分线的性质及判定
4、垂直平分线的性质及判定
新知引入
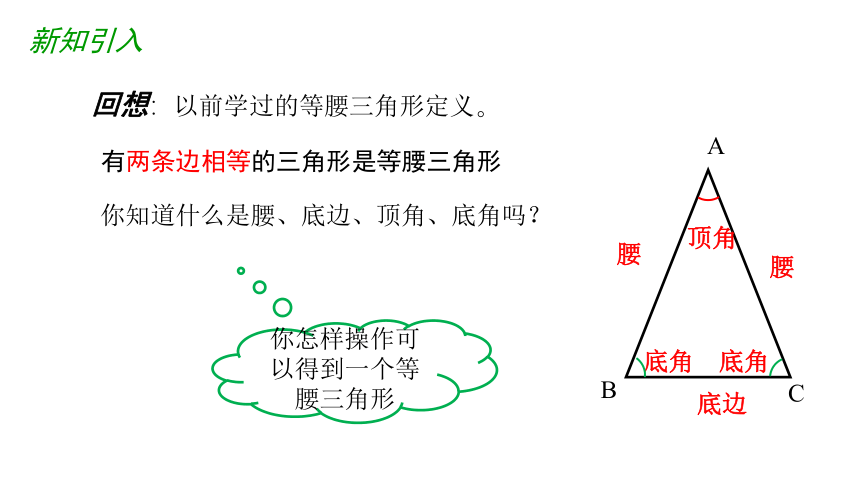
回想:以前学过的等腰三角形定义。
你知道什么是腰、底边、顶角、底角吗?
有两条边相等的三角形是等腰三角形
腰
腰
底边
底角
顶角
底角
你怎样操作可以得到一个等腰三角形
A
B
C
新知讲解
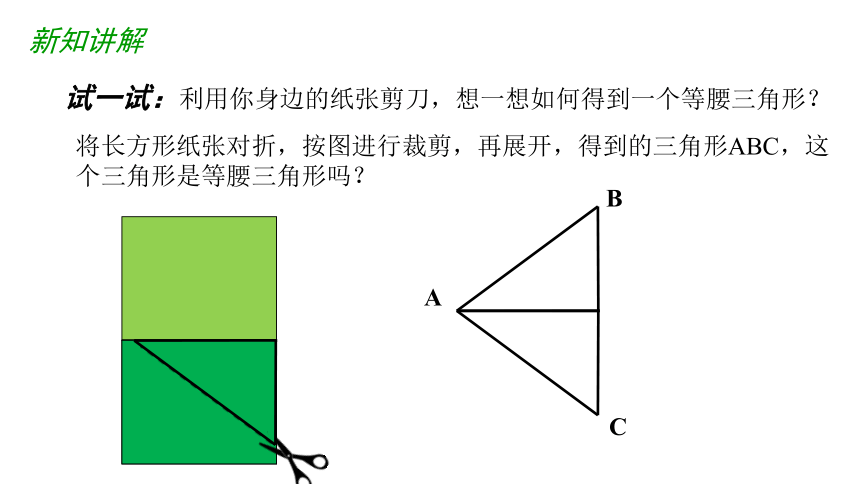
试一试:利用你身边的纸张剪刀,想一想如何得到一个等腰三角形?
将长方形纸张对折,按图进行裁剪,再展开,得到的三角形ABC,这个三角形是等腰三角形吗?
A
C
B
新知讲解
将刚才的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
重合的线段:
重合的角:
AB与AC
BD与CD
AD与AD
∠B 与∠C
∠BAD 与∠CAD
∠ADB 与∠ADC
A
C
B
D
你能发现等腰三角形的性质吗?
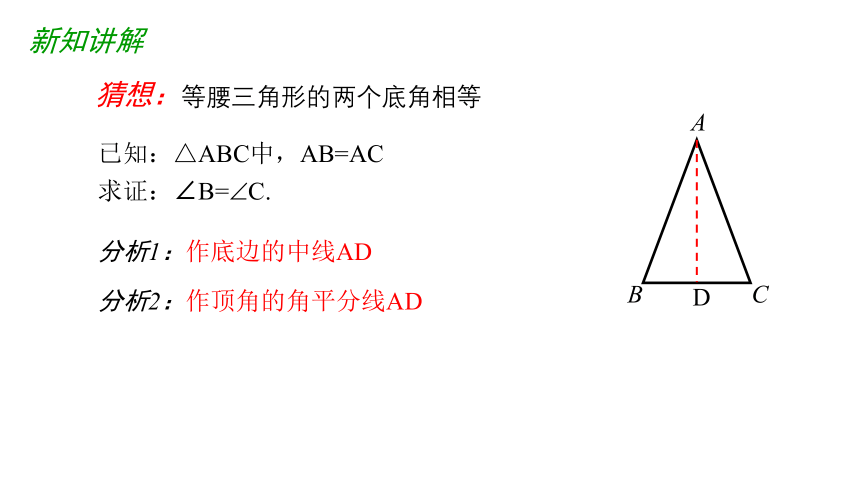
猜想:等腰三角形的两个底角相等
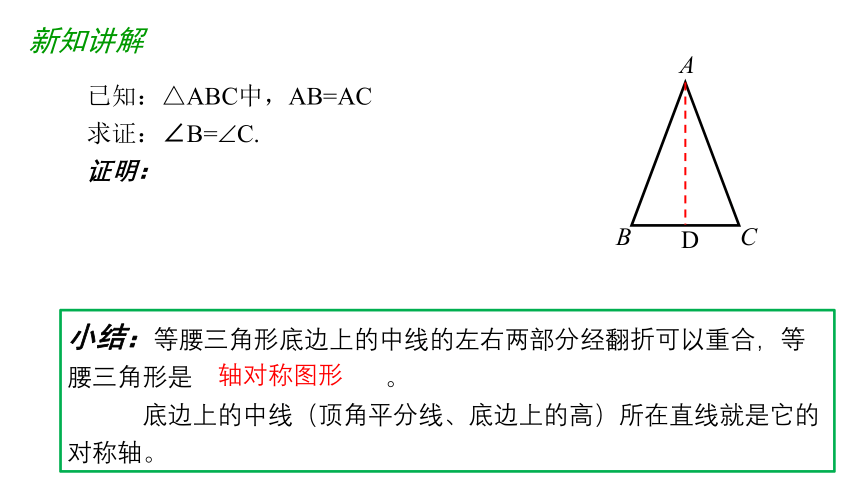
已知:△ABC中,AB=AC
求证:∠B=?C.
分析1:作底边的中线AD
分析2:作顶角的角平分线AD
A
B
C
D
新知讲解
新知讲解
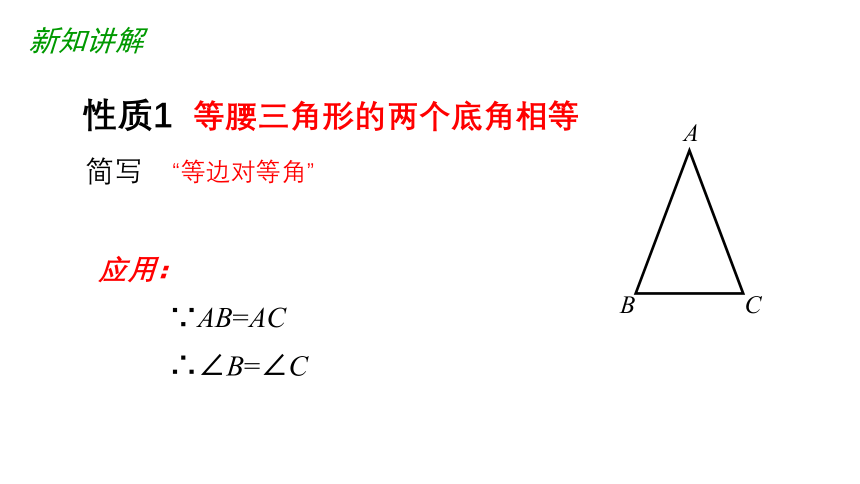
性质1 等腰三角形的两个底角相等
简写
“等边对等角”
应用:
A
B
C
∵AB=AC
∴∠B=∠C
新知讲解
思考:等腰三角形的对称轴是什么?你们说的是同一条直线吗?
请说出你的猜想。
猜想:等腰三角形顶角的平分线、底边上的中线及底边上的高线
互相重合
分析: 由△BAD≌ △CAD、还可以得出 ∠ADB=∠ADC,∠BAD=∠CAD,从而AD⊥BC.这也就证明了等腰三角形ABC底边上的中线AD平分顶角∠A并垂直于底边BC.
类似的,还可以证明等腰三角形顶角的平分线平分底边并且垂直于底边,底边上的高平分顶角且平分底边。
证明:
小结:等腰三角形底边上的中线的左右两部分经翻折可以重合,等腰三角形是 。
底边上的中线(顶角平分线、底边上的高)所在直线就是它的对称轴。
轴对称图形
已知:△ABC中,AB=AC
求证:∠B=?C.
A
B
C
D
新知讲解
新知讲解
性质2 等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合
简写
“三线合一”
应用:
A
B
C
D
∵AB=AC, ∠1=∠2(已知),
∴BD=CD,AD⊥BC(等腰三角形三线合一).
∵AB=AC, BD=CD (已知),
∴∠1=∠2,AD⊥BC(等腰三角形三线合一).
∵AB=AC, AD⊥BC(已知),
∴BD=CD, ∠1=∠2(等腰三角形三线合一).
1
2
例题精讲
例1 如图,在△ABC中 ,AB=AC,点D在AC上,且
BD=BC=AD
求:△ABC各角的度数
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
∴∠ABC= ∠C= ∠BDC=2x,
在△ABC中,∠A+∠ABC+∠C=x+2x+2x=180 °
∴x=36 °
即:∠A=36°,∠ABC=∠C=72°.
牛刀小试
如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数
C
A
D
B
∠C=38.5°, ∠B=77°.
例题精讲
例2 (1)等腰三角形的一个角是110°,它的另外两个角是多少度?
(2)等腰三角形的一个角是80°,它的另外两个角是多少度?
(1)都是35 °
(2)80 °,20 °或50 °,50 °
小结:等腰三角形两个底角相等,已知一个内角,则这个角可能是底角也可能是顶角,需分两种情况讨论
同样的,两腰相等,已知一条边,则这条边可能是腰也可能是底边,需分情况讨论
例3 如图,在△ABC中,AB=AC、DB=DC.
求证:(1)∠BAD=∠CAD;AD⊥BC.
A
B
D
C
例题精讲
1、在△ABC中, AB=AC,AB的垂直平分线与AC所在的直线相交得的锐角为50°,则底角的大小为___________.
70°或20°
学以致用
学以致用
2、如图,五角星五个角都是顶角为36 °的等腰三角形,为了画出五角星,还需要知道∠AMB的度数,∠AMB多少度?
A
A
M
B
∠AMB=108 °
3、如图,点D、E在△ABC的边BC上,AB=AC,AD=AE.
求证:BD=CE.
C
E
D
B
A
学以致用
学以致用
C
B
N
D
M
A
4、如图,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D.求∠DBC的度数。
∠DBC=30 °
学以致用
5、如图,在△ABC中,AB=AD=DC,∠BAD=26°
求:∠B和∠C的度数。
C
D
B
A
∠B=77 ° , ∠C=38.5 °
6.已知:在等腰三角形△ABC中,BD、CE是底角平分线,
∠DBC=∠F
求证:EC∥DF.
能力提升
能力提升
7、想一想:等腰三角形顶角的外角角平分线与底边有怎样的位置关系?你能给出证明吗?
C
B
A
D
E
已知:
求证:
结论:等腰三角形顶角的外角角平分线
与底边平行。
13.3 等腰三角形
13.3.1 等腰三角形
第1课时 等腰三角形的性质
温故知新
1、三角形高、角平分线、中线的定义
2、全等三角形的判定
3、角平分线的性质及判定
4、垂直平分线的性质及判定
新知引入
回想:以前学过的等腰三角形定义。
你知道什么是腰、底边、顶角、底角吗?
有两条边相等的三角形是等腰三角形
腰
腰
底边
底角
顶角
底角
你怎样操作可以得到一个等腰三角形
A
B
C
新知讲解
试一试:利用你身边的纸张剪刀,想一想如何得到一个等腰三角形?
将长方形纸张对折,按图进行裁剪,再展开,得到的三角形ABC,这个三角形是等腰三角形吗?
A
C
B
新知讲解
将刚才的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
重合的线段:
重合的角:
AB与AC
BD与CD
AD与AD
∠B 与∠C
∠BAD 与∠CAD
∠ADB 与∠ADC
A
C
B
D
你能发现等腰三角形的性质吗?
猜想:等腰三角形的两个底角相等
已知:△ABC中,AB=AC
求证:∠B=?C.
分析1:作底边的中线AD
分析2:作顶角的角平分线AD
A
B
C
D
新知讲解
新知讲解
性质1 等腰三角形的两个底角相等
简写
“等边对等角”
应用:
A
B
C
∵AB=AC
∴∠B=∠C
新知讲解
思考:等腰三角形的对称轴是什么?你们说的是同一条直线吗?
请说出你的猜想。
猜想:等腰三角形顶角的平分线、底边上的中线及底边上的高线
互相重合
分析: 由△BAD≌ △CAD、还可以得出 ∠ADB=∠ADC,∠BAD=∠CAD,从而AD⊥BC.这也就证明了等腰三角形ABC底边上的中线AD平分顶角∠A并垂直于底边BC.
类似的,还可以证明等腰三角形顶角的平分线平分底边并且垂直于底边,底边上的高平分顶角且平分底边。
证明:
小结:等腰三角形底边上的中线的左右两部分经翻折可以重合,等腰三角形是 。
底边上的中线(顶角平分线、底边上的高)所在直线就是它的对称轴。
轴对称图形
已知:△ABC中,AB=AC
求证:∠B=?C.
A
B
C
D
新知讲解
新知讲解
性质2 等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合
简写
“三线合一”
应用:
A
B
C
D
∵AB=AC, ∠1=∠2(已知),
∴BD=CD,AD⊥BC(等腰三角形三线合一).
∵AB=AC, BD=CD (已知),
∴∠1=∠2,AD⊥BC(等腰三角形三线合一).
∵AB=AC, AD⊥BC(已知),
∴BD=CD, ∠1=∠2(等腰三角形三线合一).
1
2
例题精讲
例1 如图,在△ABC中 ,AB=AC,点D在AC上,且
BD=BC=AD
求:△ABC各角的度数
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
∴∠ABC= ∠C= ∠BDC=2x,
在△ABC中,∠A+∠ABC+∠C=x+2x+2x=180 °
∴x=36 °
即:∠A=36°,∠ABC=∠C=72°.
牛刀小试
如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数
C
A
D
B
∠C=38.5°, ∠B=77°.
例题精讲
例2 (1)等腰三角形的一个角是110°,它的另外两个角是多少度?
(2)等腰三角形的一个角是80°,它的另外两个角是多少度?
(1)都是35 °
(2)80 °,20 °或50 °,50 °
小结:等腰三角形两个底角相等,已知一个内角,则这个角可能是底角也可能是顶角,需分两种情况讨论
同样的,两腰相等,已知一条边,则这条边可能是腰也可能是底边,需分情况讨论
例3 如图,在△ABC中,AB=AC、DB=DC.
求证:(1)∠BAD=∠CAD;AD⊥BC.
A
B
D
C
例题精讲
1、在△ABC中, AB=AC,AB的垂直平分线与AC所在的直线相交得的锐角为50°,则底角的大小为___________.
70°或20°
学以致用
学以致用
2、如图,五角星五个角都是顶角为36 °的等腰三角形,为了画出五角星,还需要知道∠AMB的度数,∠AMB多少度?
A
A
M
B
∠AMB=108 °
3、如图,点D、E在△ABC的边BC上,AB=AC,AD=AE.
求证:BD=CE.
C
E
D
B
A
学以致用
学以致用
C
B
N
D
M
A
4、如图,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D.求∠DBC的度数。
∠DBC=30 °
学以致用
5、如图,在△ABC中,AB=AD=DC,∠BAD=26°
求:∠B和∠C的度数。
C
D
B
A
∠B=77 ° , ∠C=38.5 °
6.已知:在等腰三角形△ABC中,BD、CE是底角平分线,
∠DBC=∠F
求证:EC∥DF.
能力提升
能力提升
7、想一想:等腰三角形顶角的外角角平分线与底边有怎样的位置关系?你能给出证明吗?
C
B
A
D
E
已知:
求证:
结论:等腰三角形顶角的外角角平分线
与底边平行。
