人教版数学八年级上册13.1.2线段的垂直平分线课件(18张)
文档属性
| 名称 | 人教版数学八年级上册13.1.2线段的垂直平分线课件(18张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 460.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 11:52:27 | ||
图片预览



文档简介
(共18张PPT)
13.1.2
线段的垂直平分线
A
B
PA=PB
P1
P1A=P1B
……
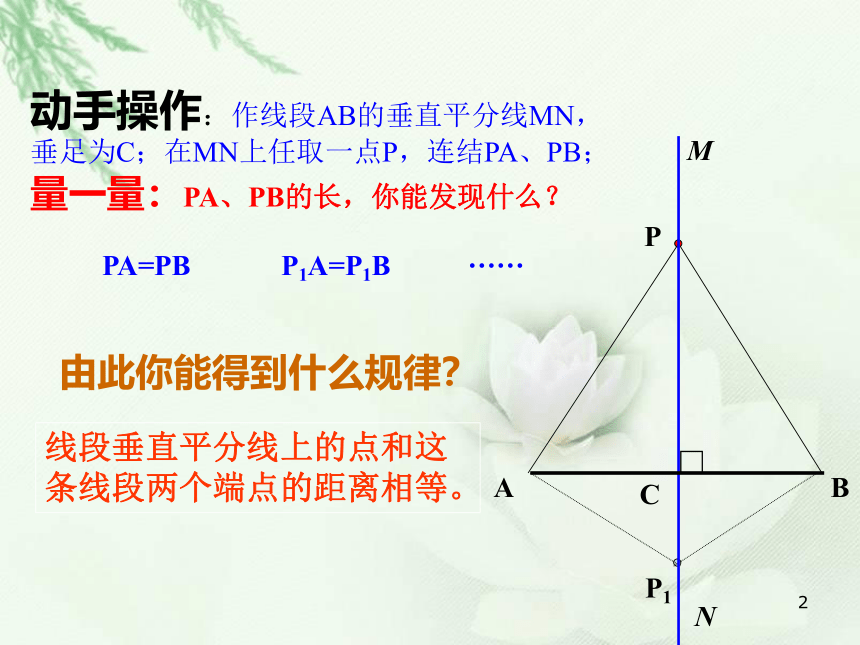
线段垂直平分线上的点和这条线段两个端点的距离相等。
P
M
N
C
动手操作:作线段AB的垂直平分线MN,垂足为C;在MN上任取一点P,连结PA、PB;量一量:PA、PB的长,你能发现什么?
由此你能得到什么规律?
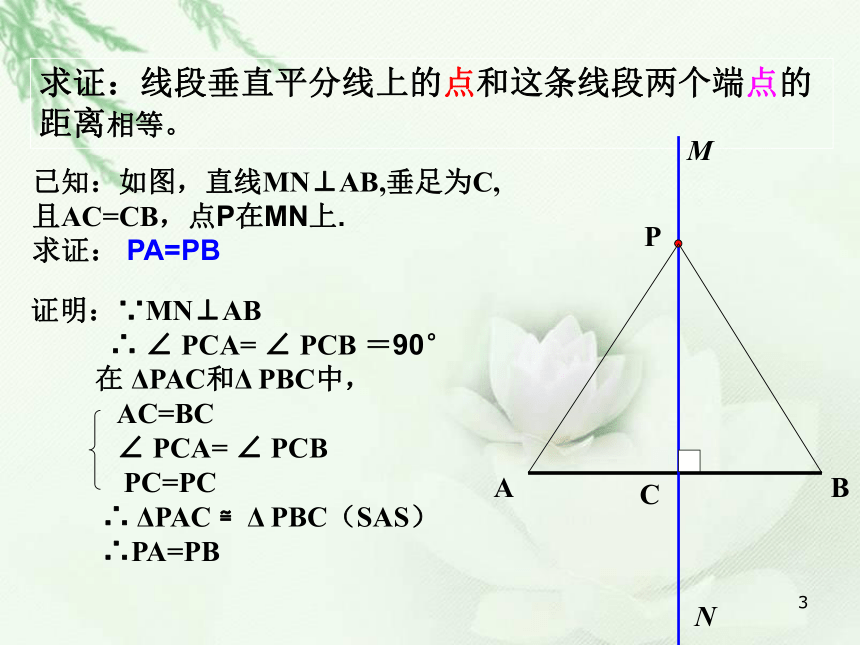
求证:线段垂直平分线上的点和这条线段两个端点的距离相等。
A
B
P
M
N
C
已知:如图,直线MN⊥AB,垂足为C,
且AC=CB,点P在MN上.
求证:
PA=PB
证明:∵MN⊥AB
∴
∠
PCA=
∠
PCB
=90°
在
ΔPAC和Δ
PBC中,
AC=BC
∠
PCA=
∠
PCB
PC=PC
∴
ΔPAC
≌Δ
PBC(SAS)
∴PA=PB
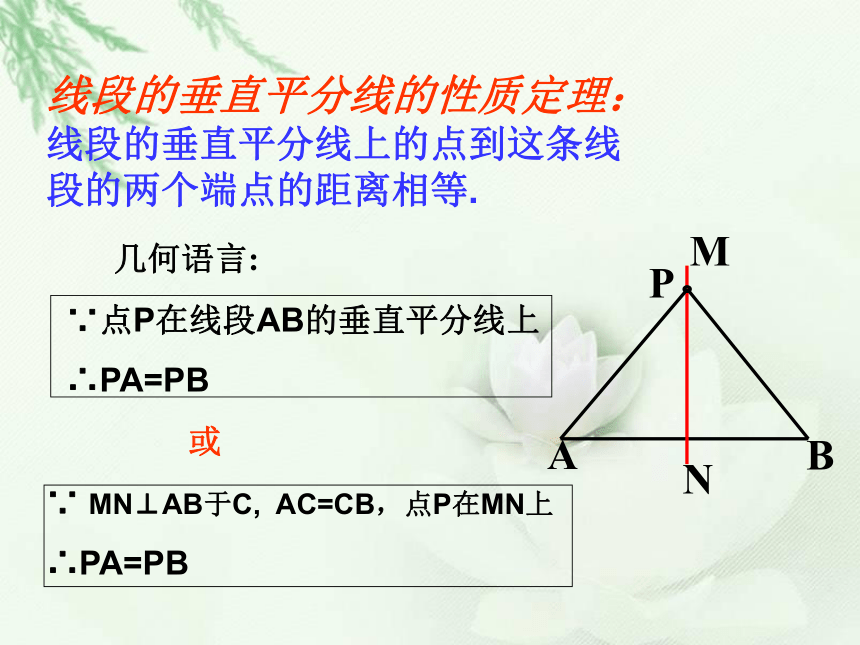
线段的垂直平分线的性质定理:线段的垂直平分线上的点到这条线段的两个端点的距离相等.
几何语言:
∵点P在线段AB的垂直平分线上
∴PA=PB
N
A
B
P
M
∵
MN⊥AB于C,
AC=CB,点P在MN上
∴PA=PB
或
1.在△ABC中,∠ACB=90°,AB=8cm,BC的垂直平分线DE交AB于D点,则CD=____
4cm
2、在△ABC,PM,QN分别垂直平分AB,AC,则:
(1)若BC=10cm则△APQ的周长=_____cm;
(2)若∠BAC=100°则∠PAQ=______.
10
200
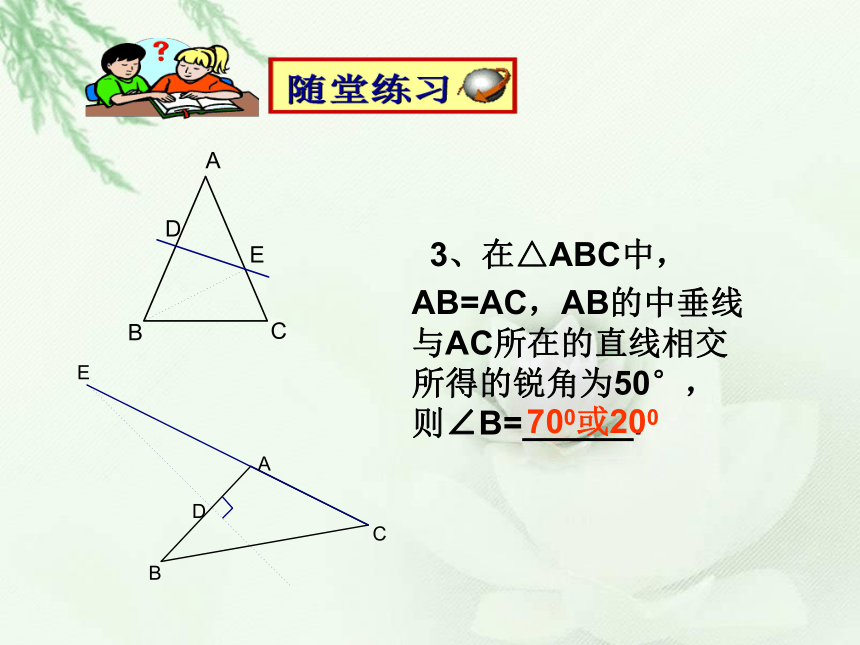
3、在△ABC中,AB=AC,AB的中垂线与AC所在的直线相交所得的锐角为50°,则∠B=______.
700或200
和一条线段的两个端点距离相等的点,在这条线段的垂直平分线上.
线段的垂直平分线上的点到这条线段两个端点的距离相等.
逆命题
求证:和一条线段的两个端点距离相等的点,在这条线段的垂直平分线上.
A
B
P
C
已知:如图,
PA=PB
求证:
点P在线段AB的垂直平分线上
证明:过点P作PC
⊥AB
于C
则
∠
PCA=
∠
PCB=90°
在
RTΔPAC和RTΔ
PBC中,
PC=PB
PC=PC
∴
ΔPAC
≌Δ
PBC(HL)
∴AC=BC
∴直线PC垂直平分线段AB
即点P在线段AB的垂直平分线上
和一条线段的两个端点距离相等的点,在这条线段的垂直平分线上.
线段的垂直平分线上的点到这条线段两个端点的距离相等.
逆命题
线段的垂直平分线可以看作是和线段两个端点距离相
等的所有点的集合
逆定理可以用来证明点在直线上(或直线经过某一点).
性质定理可以用来证明两条线段相等(或三角形是等腰三角形).
例1:尺规作图:经过已知直线外一点作这条直线的垂线。
已知:直线AB和AB外一点C。
求作:AB的垂线,使它经过点C。
作法:1、任意取一点K,使点K和点C在直线AB两旁。
2、
以C为圆心,CK长为半径作弧,交AB于点D和E。
3、分别以D和E为圆心,在于1/2DE的长为半径作弧,两弧交于点F。
4、作直线CF。直线CF既为所求。
想一想:为什么直线
CF就是所求作的垂线?
A
B
D
E
K
F
C
角的平分线
O
D
E
A
B
P
C
性质定理:
在角的平分线上的点到这个角的两边的距离相等。
逆定理:
到一个角的两边的距离相等的点,在这个角的平分线上。
角的平分线是到角的两边距离相等的所有点的集合
线段的垂直平分线
性质定
理:
线段垂直平分线上的点和这条线段两个端点的距离相等。
逆定理
:
和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合
A
B
M
N
P
求证:
三角形三边垂直平分线交于一点,且这一点到三角形三个顶点的距离相等。
证明:
∵点P在线段AB的垂直平分线MN上,
∴PA=PB(?).
同理
PB=PC.
∴PA=PC.
∴点P也在边AC的垂直平分线上,且PA=PB=PC
已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:点P也在边AC的垂直平分线上,且PA=PB=PC;
B
A
C
M
N
M’
N’
P
区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。
A
B
C
实际问题1
B
A
C
1、求作一点P,使它和已△ABC的三个顶点距离相等.
实际问题
数学化
p
PA=PB=PC
实际问题1
2、如图,在直线l上求作一点P,使PA=PB.
l
A
B
实际问题
数学化
实际问题2
P
PA=PB
数学问题源于生活实践,反过来数学又为生活实践服务
课堂练习:
1、如图,在ΔABC中,AD⊥BC于D,
AB+BD=DC。
试问:∠B与∠C是什么关系?
O
A
B
.
C
.
D
2、在V型公路(∠AOB)内部,有两个村庄C、D。你能选择一个纺织厂的厂址P,使P到V型公路的距离相等,且使C、D两村的工人上下班的路程一样吗?
小结:
本节课你有何收获?还有哪些困惑?
同学们再见
13.1.2
线段的垂直平分线
A
B
PA=PB
P1
P1A=P1B
……
线段垂直平分线上的点和这条线段两个端点的距离相等。
P
M
N
C
动手操作:作线段AB的垂直平分线MN,垂足为C;在MN上任取一点P,连结PA、PB;量一量:PA、PB的长,你能发现什么?
由此你能得到什么规律?
求证:线段垂直平分线上的点和这条线段两个端点的距离相等。
A
B
P
M
N
C
已知:如图,直线MN⊥AB,垂足为C,
且AC=CB,点P在MN上.
求证:
PA=PB
证明:∵MN⊥AB
∴
∠
PCA=
∠
PCB
=90°
在
ΔPAC和Δ
PBC中,
AC=BC
∠
PCA=
∠
PCB
PC=PC
∴
ΔPAC
≌Δ
PBC(SAS)
∴PA=PB
线段的垂直平分线的性质定理:线段的垂直平分线上的点到这条线段的两个端点的距离相等.
几何语言:
∵点P在线段AB的垂直平分线上
∴PA=PB
N
A
B
P
M
∵
MN⊥AB于C,
AC=CB,点P在MN上
∴PA=PB
或
1.在△ABC中,∠ACB=90°,AB=8cm,BC的垂直平分线DE交AB于D点,则CD=____
4cm
2、在△ABC,PM,QN分别垂直平分AB,AC,则:
(1)若BC=10cm则△APQ的周长=_____cm;
(2)若∠BAC=100°则∠PAQ=______.
10
200
3、在△ABC中,AB=AC,AB的中垂线与AC所在的直线相交所得的锐角为50°,则∠B=______.
700或200
和一条线段的两个端点距离相等的点,在这条线段的垂直平分线上.
线段的垂直平分线上的点到这条线段两个端点的距离相等.
逆命题
求证:和一条线段的两个端点距离相等的点,在这条线段的垂直平分线上.
A
B
P
C
已知:如图,
PA=PB
求证:
点P在线段AB的垂直平分线上
证明:过点P作PC
⊥AB
于C
则
∠
PCA=
∠
PCB=90°
在
RTΔPAC和RTΔ
PBC中,
PC=PB
PC=PC
∴
ΔPAC
≌Δ
PBC(HL)
∴AC=BC
∴直线PC垂直平分线段AB
即点P在线段AB的垂直平分线上
和一条线段的两个端点距离相等的点,在这条线段的垂直平分线上.
线段的垂直平分线上的点到这条线段两个端点的距离相等.
逆命题
线段的垂直平分线可以看作是和线段两个端点距离相
等的所有点的集合
逆定理可以用来证明点在直线上(或直线经过某一点).
性质定理可以用来证明两条线段相等(或三角形是等腰三角形).
例1:尺规作图:经过已知直线外一点作这条直线的垂线。
已知:直线AB和AB外一点C。
求作:AB的垂线,使它经过点C。
作法:1、任意取一点K,使点K和点C在直线AB两旁。
2、
以C为圆心,CK长为半径作弧,交AB于点D和E。
3、分别以D和E为圆心,在于1/2DE的长为半径作弧,两弧交于点F。
4、作直线CF。直线CF既为所求。
想一想:为什么直线
CF就是所求作的垂线?
A
B
D
E
K
F
C
角的平分线
O
D
E
A
B
P
C
性质定理:
在角的平分线上的点到这个角的两边的距离相等。
逆定理:
到一个角的两边的距离相等的点,在这个角的平分线上。
角的平分线是到角的两边距离相等的所有点的集合
线段的垂直平分线
性质定
理:
线段垂直平分线上的点和这条线段两个端点的距离相等。
逆定理
:
和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合
A
B
M
N
P
求证:
三角形三边垂直平分线交于一点,且这一点到三角形三个顶点的距离相等。
证明:
∵点P在线段AB的垂直平分线MN上,
∴PA=PB(?).
同理
PB=PC.
∴PA=PC.
∴点P也在边AC的垂直平分线上,且PA=PB=PC
已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:点P也在边AC的垂直平分线上,且PA=PB=PC;
B
A
C
M
N
M’
N’
P
区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。
A
B
C
实际问题1
B
A
C
1、求作一点P,使它和已△ABC的三个顶点距离相等.
实际问题
数学化
p
PA=PB=PC
实际问题1
2、如图,在直线l上求作一点P,使PA=PB.
l
A
B
实际问题
数学化
实际问题2
P
PA=PB
数学问题源于生活实践,反过来数学又为生活实践服务
课堂练习:
1、如图,在ΔABC中,AD⊥BC于D,
AB+BD=DC。
试问:∠B与∠C是什么关系?
O
A
B
.
C
.
D
2、在V型公路(∠AOB)内部,有两个村庄C、D。你能选择一个纺织厂的厂址P,使P到V型公路的距离相等,且使C、D两村的工人上下班的路程一样吗?
小结:
本节课你有何收获?还有哪些困惑?
同学们再见
