人教版数学九年级上册 24.1.3弧、弦、圆心角课件(23张)
文档属性
| 名称 | 人教版数学九年级上册 24.1.3弧、弦、圆心角课件(23张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 10:36:33 | ||
图片预览





文档简介
24.1.3 弧、弦、圆心角
人教版九年级上册
创设情境 导入新课
创设情境 导入新课
创设情境 导入新课
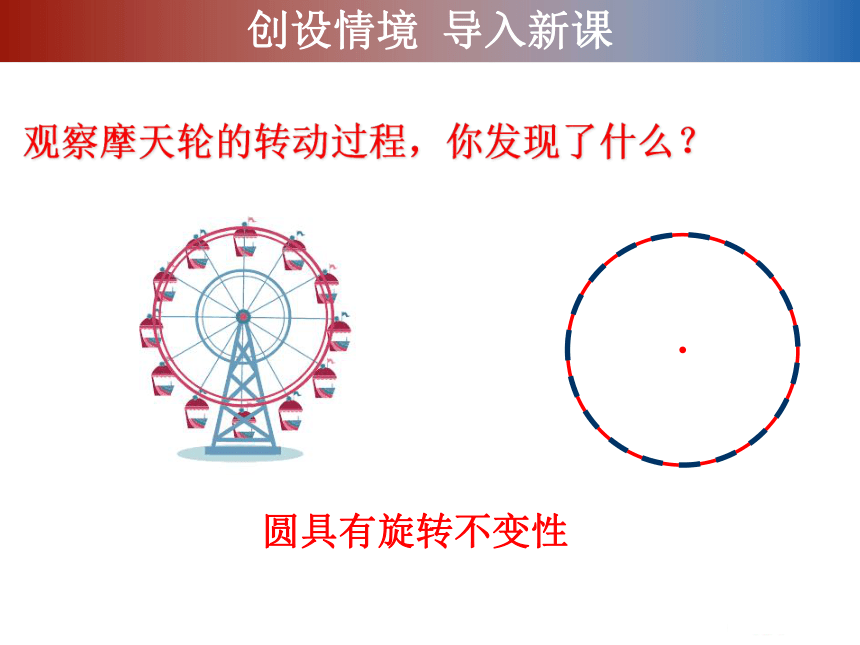
圆具有旋转不变性
观察摩天轮的转动过程,你发现了什么?
·
创设情境 导入新课
·
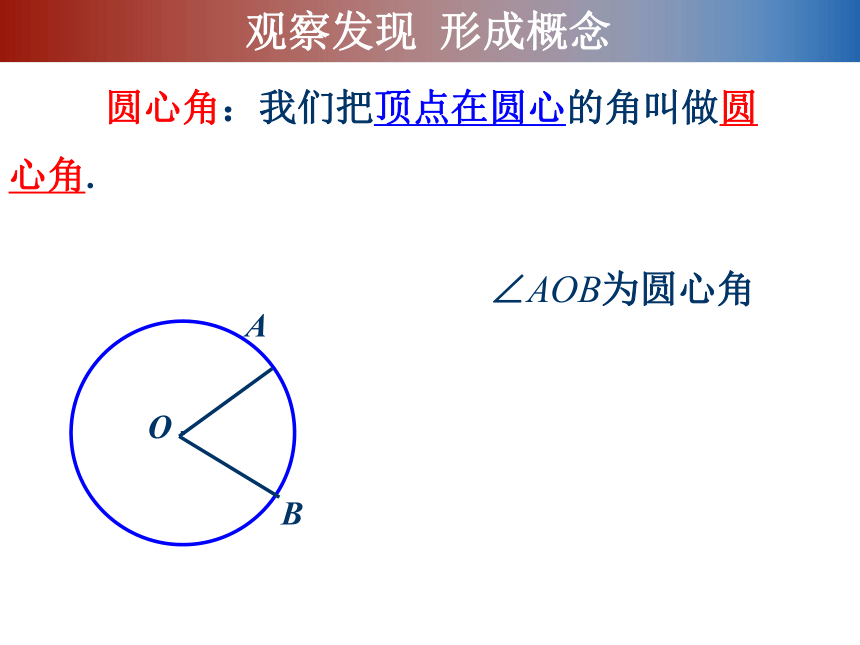
圆心角:我们把顶点在圆心的角叫做圆心角.
O
B
A
∠AOB为圆心角
观察发现 形成概念
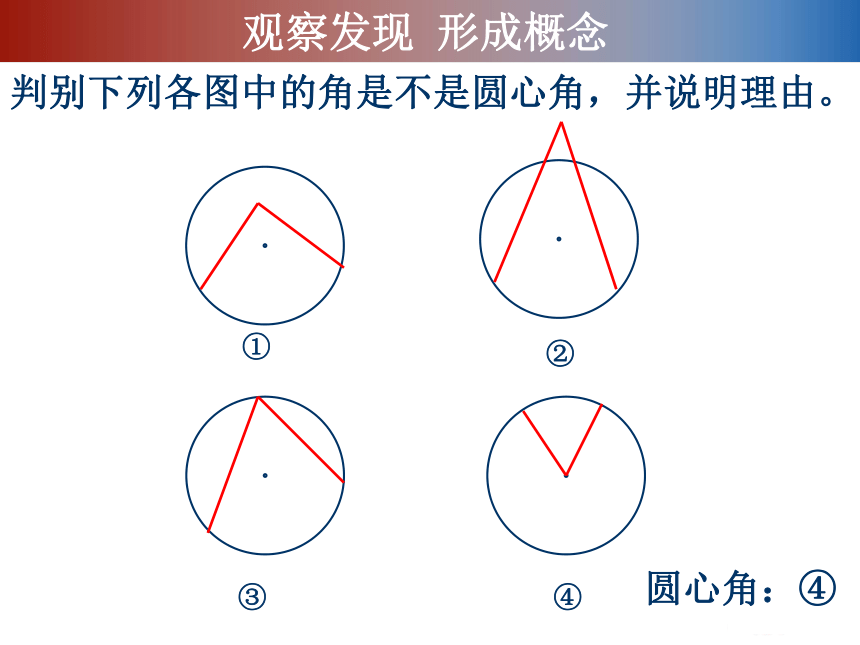
判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
圆心角:④
观察发现 形成概念
·
O
B
A
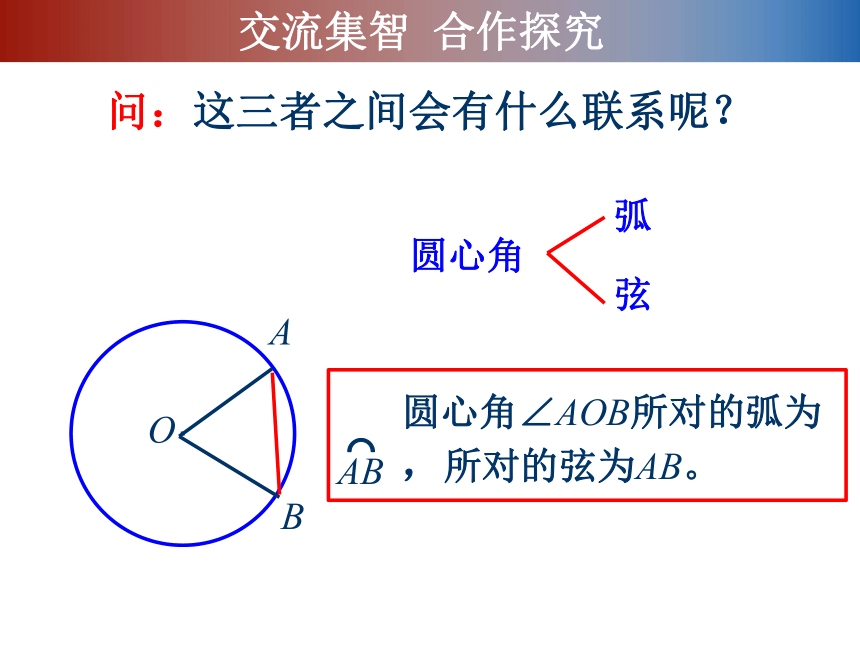
圆心角∠AOB所对的弧为AB
⌒
交流集智 合作探究
,所对的弦为AB。
问:这三者之间会有什么联系呢?
圆心角
弧
弦
如图,已知∠AOB=∠A1OB1,它们所对的弧AB
和A1B1、所对的弦AB和A1B1相等吗?为什么?
·
O
A
B
A1
B1
∵ ∠AOB=∠A1OB1
∴AB=A1B1 ,AB=A1B1 .
⌒
⌒
交流集智 合作探究
⌒
⌒
·
O
A
B
A1
·
O1
B1
·
如图,⊙O与⊙O1是等圆时,∠AOB =∠A1OB1,请问上述结论还成立吗?为什么?
∵ ∠AOB=∠A1OB1
∴AB=A1B1 ,AB=A1B1 .
⌒
⌒
交流集智 合作探究
O
α
A
B
A1
B1
α
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
∵ ∠AOB=∠A1OB1
∴AB=A1B1 ,AB=A1B1 .
⌒
⌒
定理:
交流集智 合作探究
猜想:
在同圆或等圆中,如果两条弧相等,你能得什么结论?
在同圆或等圆中,如果两条弦相等呢?
交流集智 合作探究
·
O
A
B
A1
B1
·
O
A
B
A1
·
O1
B1
·
同圆
等圆
交流集智 合作探究
同样,还可以得到:
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角_____, 所对的弦________;
在同圆或等圆中,如果两条弦相等,那么他们所对的圆心角______,所对的弧_________.
定理:
相等
相等
相等
相等
在同圆或等圆中,相等的圆心角所对的弧
相等,所对的弦也相等
交流集智 合作探究
试判断下列命题的真假:
1、相等的圆心角所对的弧相等 ( )
2、长度相等的两条弧是等弧 ( )
3、等弦所对的圆心角相等 ( )
4、等弧所对的弦相等 ( )
假
假
假
真
命题辨析 加深理解
O
α
A
B
A1
B1
α
同圆或等圆中,两个圆心角、两条圆心角所对的弧、两条圆心角所对的弦中如果有一组量相等,它们所对应的其余各组量有什么关系?
交流集智 合作探究
相等
(1) 圆心角
(2) 弧
(3) 弦
知一推二
O
α
A
B
A1
B1
α
归纳总结:
归纳总结 提炼升华
已知:如图,AB是⊙O的直径,BC=CD=DE,∠COD=35°,求∠AOE的度数。
O
A
B
E
D
C
证明:∵ BC=CD=DE
∴∠COB=∠COD=∠DOE=35°
∴∠AOE=180°-∠COB-∠COD-∠DOE
=75°
⌒
⌒
⌒
⌒
⌒
⌒
学以致用 巩固练习
证明: ∵ AB=AC
∴ AB=AC
又 ∠ACB=60°
∴ △ABC是等边三角形,
∴ AB=BC=CA
∴∠AOB=∠BOC=∠AOC
已知:如图,在⊙O中,AB=AC,∠ACB=60°.
求证:∠AOB=∠BOC=∠AOC.
⌒
⌒
⌒
⌒
O
B
C
A
(在同圆中,相等的弧所对的弦相等)
(在同圆中,相等的弦所对的圆心角相等)
典型例题 解疑释难
已知:如图,在⊙O中,∠BOC=120°,∠ACO=30°.
求证:AB=AC=BC.
⌒
O
B
C
A
变式训练 展示提升
1、本节课学习了哪些内容?
3、探索弧、弦、圆心角之间的关系时,利用了圆的什么性质?是如何论证它们之间的关系的?
O
α
A
B
A1
B1
α
课堂小结 反思提高
2、在同圆或等圆中,对应的
弧、弦、圆心角之间有什么关系?
O
B
A
C
D
F
E
1、必做题:教科书习题24.1第3、4题.
2、选做题:已知:如图,⊙O的两条半径OA⊥OB,C、D是弧AB的三等分点。求证:CD=AE=BF。(提示:连接AC、BD)
达标检测 拓展延伸
同学们,再见!
人教版九年级上册
创设情境 导入新课
创设情境 导入新课
创设情境 导入新课
圆具有旋转不变性
观察摩天轮的转动过程,你发现了什么?
·
创设情境 导入新课
·
圆心角:我们把顶点在圆心的角叫做圆心角.
O
B
A
∠AOB为圆心角
观察发现 形成概念
判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
圆心角:④
观察发现 形成概念
·
O
B
A
圆心角∠AOB所对的弧为AB
⌒
交流集智 合作探究
,所对的弦为AB。
问:这三者之间会有什么联系呢?
圆心角
弧
弦
如图,已知∠AOB=∠A1OB1,它们所对的弧AB
和A1B1、所对的弦AB和A1B1相等吗?为什么?
·
O
A
B
A1
B1
∵ ∠AOB=∠A1OB1
∴AB=A1B1 ,AB=A1B1 .
⌒
⌒
交流集智 合作探究
⌒
⌒
·
O
A
B
A1
·
O1
B1
·
如图,⊙O与⊙O1是等圆时,∠AOB =∠A1OB1,请问上述结论还成立吗?为什么?
∵ ∠AOB=∠A1OB1
∴AB=A1B1 ,AB=A1B1 .
⌒
⌒
交流集智 合作探究
O
α
A
B
A1
B1
α
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
∵ ∠AOB=∠A1OB1
∴AB=A1B1 ,AB=A1B1 .
⌒
⌒
定理:
交流集智 合作探究
猜想:
在同圆或等圆中,如果两条弧相等,你能得什么结论?
在同圆或等圆中,如果两条弦相等呢?
交流集智 合作探究
·
O
A
B
A1
B1
·
O
A
B
A1
·
O1
B1
·
同圆
等圆
交流集智 合作探究
同样,还可以得到:
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角_____, 所对的弦________;
在同圆或等圆中,如果两条弦相等,那么他们所对的圆心角______,所对的弧_________.
定理:
相等
相等
相等
相等
在同圆或等圆中,相等的圆心角所对的弧
相等,所对的弦也相等
交流集智 合作探究
试判断下列命题的真假:
1、相等的圆心角所对的弧相等 ( )
2、长度相等的两条弧是等弧 ( )
3、等弦所对的圆心角相等 ( )
4、等弧所对的弦相等 ( )
假
假
假
真
命题辨析 加深理解
O
α
A
B
A1
B1
α
同圆或等圆中,两个圆心角、两条圆心角所对的弧、两条圆心角所对的弦中如果有一组量相等,它们所对应的其余各组量有什么关系?
交流集智 合作探究
相等
(1) 圆心角
(2) 弧
(3) 弦
知一推二
O
α
A
B
A1
B1
α
归纳总结:
归纳总结 提炼升华
已知:如图,AB是⊙O的直径,BC=CD=DE,∠COD=35°,求∠AOE的度数。
O
A
B
E
D
C
证明:∵ BC=CD=DE
∴∠COB=∠COD=∠DOE=35°
∴∠AOE=180°-∠COB-∠COD-∠DOE
=75°
⌒
⌒
⌒
⌒
⌒
⌒
学以致用 巩固练习
证明: ∵ AB=AC
∴ AB=AC
又 ∠ACB=60°
∴ △ABC是等边三角形,
∴ AB=BC=CA
∴∠AOB=∠BOC=∠AOC
已知:如图,在⊙O中,AB=AC,∠ACB=60°.
求证:∠AOB=∠BOC=∠AOC.
⌒
⌒
⌒
⌒
O
B
C
A
(在同圆中,相等的弧所对的弦相等)
(在同圆中,相等的弦所对的圆心角相等)
典型例题 解疑释难
已知:如图,在⊙O中,∠BOC=120°,∠ACO=30°.
求证:AB=AC=BC.
⌒
O
B
C
A
变式训练 展示提升
1、本节课学习了哪些内容?
3、探索弧、弦、圆心角之间的关系时,利用了圆的什么性质?是如何论证它们之间的关系的?
O
α
A
B
A1
B1
α
课堂小结 反思提高
2、在同圆或等圆中,对应的
弧、弦、圆心角之间有什么关系?
O
B
A
C
D
F
E
1、必做题:教科书习题24.1第3、4题.
2、选做题:已知:如图,⊙O的两条半径OA⊥OB,C、D是弧AB的三等分点。求证:CD=AE=BF。(提示:连接AC、BD)
达标检测 拓展延伸
同学们,再见!
同课章节目录
