北师大版九年级数学上册第三章概率的进一步认识过关与测试(word版含答案)
文档属性
| 名称 | 北师大版九年级数学上册第三章概率的进一步认识过关与测试(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 255.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 13:59:22 | ||
图片预览




文档简介
第三章过关与测试
(时间:120分钟 满分:150分)
题 号
一
二
三
总 分
得 分
一、选择题(本大题共15小题,每小题3分,共45分.每小题只有一个正确选项)
1.对“某市明天下雨的概率是75%”这句话,理解正确的是( )
A.某市明天将有75%的时间下雨 B.某市明天将有75%的地区下雨
C.某市明天一定下雨 D.某市明天下雨的可能性较大
2.同时抛掷两枚质地均匀的硬币,两枚硬币全部正面向上的概率为( )
A.14 B.13 C.12 D.34
3.在课外实践活动中,甲、乙、丙、丁四个小组用投掷一元硬币的方法估算正面朝上的概率,其试验次数分别为10次、50次、100次、200次,其中试验相对科学的是( )
A.甲组 B.乙组 C.丙组 D.丁组
4.在一个不透明的袋子中有20个除颜色外均相同的小球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复摸球试验后,发现摸到红球的频率稳定于0.4,由此可估计袋中红球的个数为( )
A.4 B.6 C.8 D.12
5.小亮、小莹、大刚三位同学随机地站成一排合影留念,小亮恰好站在中间的概率是( )
A.12 B.13 C.23 D.16
6.从长为3,5,7,10的四条线段中任意选取三条作为边,能构成三角形的概率是( )
A.14 B.12 C.34 D.1
7.从-2,-1,2这三个数中任取两个不同的数相乘,积为正数的概率是( )
A.23 B.12 C.13 D.14
8.袋中装有编号为1,2,3的三个质地均匀、大小相同的球,从中随机取出一球记下编号后,放入袋中搅匀,再从袋中随机取出一球,两次所取球的编号相同的概率为( )
A.12 B.13 C.16 D.19
9.甲箱内有4个球,颜色分别为红、黄、绿、蓝;乙箱内有3个球,颜色分别为红、黄、黑,小明打算同时从甲、乙两个箱子中各取出一个球,若同一箱中每球被取出的机会相等,则小明取出的两个球颜色相同的概率是( )
A.13 B.16 C.27 D.712
10.下列模拟掷硬币的试验不正确的是( )
A.用计算器随机地取数,取奇数相当于硬币正面朝上,取偶数相当于硬币正面朝下
B.袋中装两个小球,分别标上1和2,随机地摸球,摸出1表示硬币正面朝上
C.在没有大小王的扑克牌中随机地抽一张牌,抽到红色牌表示硬币正面朝上
D.将1,2,3,4,5分别写在5张纸上,并搓成团,每次随机地取一个,取到奇数号表示硬币正面朝上
11.质地均匀的骰子六个面分别刻有1到6的点数,掷两次骰子,得到向上一面的两个点数,则下列事件中,发生可能性最大的是( )
A.点数都是偶数 B.点数的和为奇数
C.点数的和小于13 D.点数的和小于2
12.小强、小亮、小文三位同学玩投硬币游戏.三人同时各投出一枚均匀硬币,若出现3个正面向上或3个反面向上,则小强赢;若出现2个正面向上1个反面向上,则小亮赢;若出现1个正面向上2个反面向上,则小文赢.下面说法正确的是( )
A.小强赢的概率最小 B.小文赢的概率最小
C.小亮赢的概率最小 D.三人赢的概率都相等
13.如图所示,小明、小刚利用两个转盘进行游戏;规则为小明将两个转盘各转一次,如配成紫色(红与蓝)得5分,否则小刚得3分,此规则对小明和小刚( )
A.公平 B.对小明有利 C.对小刚有利 D.不可预测
14.若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数,如796就是一个“中高数”.若十位上数字为7,则从3,4,5,6,8,9中任选两数,与7组成“中高数”的概率是( )
A.12 B.23 C.25 D.35
15.下图显示了用计算机模拟随机投掷一枚图钉的某次试验的结果.
下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着试验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟试验,则当投掷次数为1 000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A.① B.② C.①② D.①③
二、填空题(本大题共5小题,每题5分,共25分)
16.从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
种子粒数
100
400
800
1 000
2 000
5 000
发芽种子粒数
85
298
652
793
1 604
4 005
发芽频率
0.850
0.745
0.815
0.793
0.802
0.801
根据以上数据可以估计,该玉米种子发芽的概率约为 (精确到0.1).?
17.在一个不透明的空袋子里,放入仅颜色不同的2个红球和1个白球,从中随机摸出1个球后不放回,再从中随机摸出1个球,两次都摸到红球的概率是 .?
18.从-1,0,1,2这四个数中,任取两个不同的数作为点的坐标,则该点在第一象限的概率为 .?
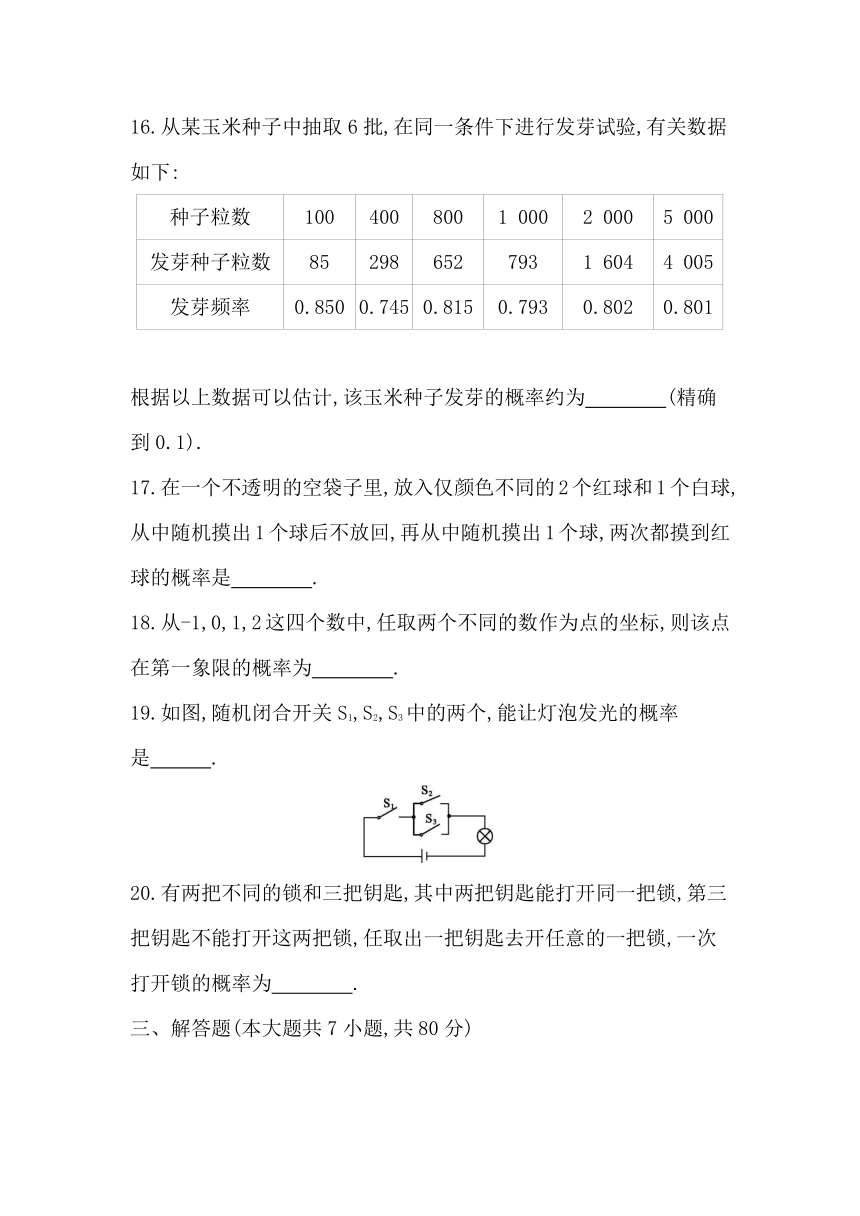
19.如图,随机闭合开关S1,S2,S3中的两个,能让灯泡发光的概率是 .?
20.有两把不同的锁和三把钥匙,其中两把钥匙能打开同一把锁,第三把钥匙不能打开这两把锁,任取出一把钥匙去开任意的一把锁,一次打开锁的概率为 .?
三、解答题(本大题共7小题,共80分)
21.(8分)小明代表学校参加“我和我的祖国”主题宣传教育活动.该活动分为两个阶段,第一阶段有“歌曲演唱”“书法展示”“器乐独奏”3个项目(依次用A,B,C表示),第二阶段有“故事演讲”“诗歌朗诵”2个项目(依次用D,E表示),参加人员在每个阶段各随机抽取一个项目完成.用画树状图或列表的方法列出小明参加项目的所有等可能的结果,并求小明恰好抽中B,D两个项目的概率.
22.(8分)为增强学生的环保意识,某中学举办了环保知识竞赛,某班共有5名学生(3名男生、2名女生)获奖.
(1)老师若从获奖的5名学生中选取一名作为班级的“环保小卫士”,则恰好是男生的概率为 .?
(2)老师若从获奖的5名学生中任选两名作为班级的“环保小卫士”,请用画树状图法或列表法,求出恰好是一名男生、一名女生的概率.
23.(10分)阅读对话,解答问题:
(1)分别用a,b表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字,请用画树状图法或列表法写出(a,b)的所有取值.
(2)求在(a,b)中使关于x的一元二次方程x2-ax+2b=0有实数根的概率.
24.(12分)某校5月份举行了八年级生物实验考查,有A和B两个考查实验,规定每位学生只参加其中一个实验的考查,并由学生自己抽签决定具体的考查实验,小明、小丽、小华都参加了本次考查.
(1)小丽参加实验A考查的概率是 .?
(2)用列表或画树状图的方法求小明、小丽都参加实验A考查的概率.
(3)他们三人都参加实验A考查的概率是 .?
25.(12分)为了参加中考体育测试,甲、乙、丙三位同学进行足球传球训练.球从一个人脚下随机传到另一个人脚下,且每位传球人传球给其余两人的机会是均等的,由甲开始传球,共传三次.
(1)用树状图列举出三次传球的所有等可能情况.
(2)求传球三次后,球回到甲脚下的概率.
(3)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
26.(14分)在一个不透明的口袋里有分别标注2,4,6的3个小球(小球除数字不同外,其余都相同),另有3张背面完全一样、正面分别写有数字6,7,8的卡片.现从口袋中任意摸出一个小球,再从这3张背面朝上的卡片中任意摸出一张卡片.
(1)请你用列表或画树状图的方法,表示出所有等可能出现的结果.
(2)小红和小莉做游戏,制定了两个游戏规则:
规则1:若两次摸出的数字,至少有一次是“6”,小红赢;否则,小莉赢.
规则2:若摸出的卡片上的数字是球上数字的整数倍时,小红赢;否则,小莉赢.
小红要想在游戏中获胜,她会选择哪一种规则,并说明理由.
27.(16分)电子政务、数字经济、智慧社会…一场数字革命正在神州大地激荡.在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整):
“掌握新技术,走进数时代”信息技术
应用大赛成绩频数分布统计表 “掌握新技术,走进数时代”信息
技术应用大赛成绩扇形统计图
组别
成绩x(分)
人数
A
60≤x<70
10
B
70≤x<80
m
C
80≤x<90
16
D
90≤x≤100
4
请观察上面的图表,解答下列问题:
(1)统计表中m= ;统计图中n= ,D组的圆心角是 度.?
(2)D组的4名学生中,有2名男生和2名女生.从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法,求:
①恰好1名男生和1名女生被抽取参加5G体验活动的概率;
②至少1名女生被抽取参加5G体验活动的概率.
第三章过关与测试
1.D 2.A 3.D 4.C 5.B 6.B 7.C 8.B 9.B 10.D 11.C 12.A 13.A 14.C 15.B 16.0.8 17.13 18.16 19.23 20.13
21.解:画树状图如图所示.
由树状图知共有6种等可能结果,其中小明恰好抽中B,D两个项目的只有1种情况,
所以小明恰好抽中B,D两个项目的概率为16.
22.解:(1)由于5名学生中共有男生3名,所以抽到男生的概率为35,
故答案为35.
(2)画树状图为:
共有20种等可能的结果数,其中选出1名男生和1名女生的结果为12种,所以恰好选出1名男生和1名女生的概率为1220=35.
23.解:(1)(a,b)对应的表格为:
b
a
1
2
3
1
(1,1)
(1,2)
(1,3)
2
(2,1)
(2,2)
(2,3)
3
(3,1)
(3,2)
(3,3)
4
(4,1)
(4,2)
(4,3)
(2)∵方程x2-ax+2b=0有实数根,∴Δ=a2-8b≥0.
∴使a2-8b≥0的(a,b)有(3,1),(4,1),(4,2),
∴P(有实数根)=312=14.
24.解:(1)由于只有A和B两个考查实验,所以小丽参加实验A考查的概率是12,故答案为12.
(2)画树状图如图所示.∵两人参加的实验考查共有四种等可能结果,而两人均参加实验A考查有1种,∴小明、小丽都参加实验A考查的概率为14.
(3)由列表或画树状图可知,他们参加实验考查的情况共有8种,而他们均参加实验A考查的情况只有1种,所以他们三人都参加实验A考查的概率为18.故答案为18.
25.解:(1)三次传球所有等可能的情况如图:
(2)由上图知:三次传球后,球回到甲的概率为P(甲)=28=14.
(3)由上图知:三次传球后,球回到乙的概率为P(乙)=38,
P(乙)>P(甲),所以球传到乙脚下的概率要大.
26.解:(1)列表如下:
卡片
小球
6
7
8
2
(2,6)
(2,7)
(2,8)
4
(4,6)
(4,7)
(4,8)
6
(6,6)
(6,7)
(6,8)
画树状图如图所示:
共有9种等可能结果,分别是(2,6),(2,7),(2,8),(4,6),(4,7),(4,8),(6,6),(6,7),(6,8).
(2)从表格或树状图可知,至少有一次是“6”的情况有5种,所以,小红赢的概率是P(至少有一次是“6”)=59,小莉赢的概率是49,
∵59>49,∴此规则小红获胜的概率大.
卡片上的数字是球上数字的整数倍的有:(2,6),(2,8),(4,8),(6,6),共4种情况,所以,小红赢的概率是P(卡片上的数字是球上数字的整数倍)=49,小莉赢的概率是59,
∵59>49,∴此规则小莉获胜的概率大,
∴小红要想在游戏中获胜,她应该选择规则1.
27.解:(1)被调查的总人数为10÷20%=50,
则m=50-(10+16+4)=20,n%=1650×100%=32%,即n=32,
D组的圆心角是360°×450=28.8°.
(2)①设男同学标记为A,B;女学生标记为1,2,可能出现的所有结果列表如下:
A
B
1
2
A
/
(B,A)
(1,A)
(2,A)
B
(A,B)
/
(1,B)
(2,B)
1
(A,1)
(B,1)
/
(2,1)
2
(A,2)
(B,2)
(1,2)
/
共有12种等可能的结果,其中刚好抽到一男一女的结果有8种,
∴恰好1名男生和1名女生被抽取参加5G体验活动的概率为812=23;
②∵至少1名女生被抽取参加5G体验活动的有10种结果,
∴至少1名女生被抽取参加5G体验活动的概率为1012=56.
(时间:120分钟 满分:150分)
题 号
一
二
三
总 分
得 分
一、选择题(本大题共15小题,每小题3分,共45分.每小题只有一个正确选项)
1.对“某市明天下雨的概率是75%”这句话,理解正确的是( )
A.某市明天将有75%的时间下雨 B.某市明天将有75%的地区下雨
C.某市明天一定下雨 D.某市明天下雨的可能性较大
2.同时抛掷两枚质地均匀的硬币,两枚硬币全部正面向上的概率为( )
A.14 B.13 C.12 D.34
3.在课外实践活动中,甲、乙、丙、丁四个小组用投掷一元硬币的方法估算正面朝上的概率,其试验次数分别为10次、50次、100次、200次,其中试验相对科学的是( )
A.甲组 B.乙组 C.丙组 D.丁组
4.在一个不透明的袋子中有20个除颜色外均相同的小球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复摸球试验后,发现摸到红球的频率稳定于0.4,由此可估计袋中红球的个数为( )
A.4 B.6 C.8 D.12
5.小亮、小莹、大刚三位同学随机地站成一排合影留念,小亮恰好站在中间的概率是( )
A.12 B.13 C.23 D.16
6.从长为3,5,7,10的四条线段中任意选取三条作为边,能构成三角形的概率是( )
A.14 B.12 C.34 D.1
7.从-2,-1,2这三个数中任取两个不同的数相乘,积为正数的概率是( )
A.23 B.12 C.13 D.14
8.袋中装有编号为1,2,3的三个质地均匀、大小相同的球,从中随机取出一球记下编号后,放入袋中搅匀,再从袋中随机取出一球,两次所取球的编号相同的概率为( )
A.12 B.13 C.16 D.19
9.甲箱内有4个球,颜色分别为红、黄、绿、蓝;乙箱内有3个球,颜色分别为红、黄、黑,小明打算同时从甲、乙两个箱子中各取出一个球,若同一箱中每球被取出的机会相等,则小明取出的两个球颜色相同的概率是( )
A.13 B.16 C.27 D.712
10.下列模拟掷硬币的试验不正确的是( )
A.用计算器随机地取数,取奇数相当于硬币正面朝上,取偶数相当于硬币正面朝下
B.袋中装两个小球,分别标上1和2,随机地摸球,摸出1表示硬币正面朝上
C.在没有大小王的扑克牌中随机地抽一张牌,抽到红色牌表示硬币正面朝上
D.将1,2,3,4,5分别写在5张纸上,并搓成团,每次随机地取一个,取到奇数号表示硬币正面朝上
11.质地均匀的骰子六个面分别刻有1到6的点数,掷两次骰子,得到向上一面的两个点数,则下列事件中,发生可能性最大的是( )
A.点数都是偶数 B.点数的和为奇数
C.点数的和小于13 D.点数的和小于2
12.小强、小亮、小文三位同学玩投硬币游戏.三人同时各投出一枚均匀硬币,若出现3个正面向上或3个反面向上,则小强赢;若出现2个正面向上1个反面向上,则小亮赢;若出现1个正面向上2个反面向上,则小文赢.下面说法正确的是( )
A.小强赢的概率最小 B.小文赢的概率最小
C.小亮赢的概率最小 D.三人赢的概率都相等
13.如图所示,小明、小刚利用两个转盘进行游戏;规则为小明将两个转盘各转一次,如配成紫色(红与蓝)得5分,否则小刚得3分,此规则对小明和小刚( )
A.公平 B.对小明有利 C.对小刚有利 D.不可预测
14.若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数,如796就是一个“中高数”.若十位上数字为7,则从3,4,5,6,8,9中任选两数,与7组成“中高数”的概率是( )
A.12 B.23 C.25 D.35
15.下图显示了用计算机模拟随机投掷一枚图钉的某次试验的结果.
下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着试验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟试验,则当投掷次数为1 000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A.① B.② C.①② D.①③
二、填空题(本大题共5小题,每题5分,共25分)
16.从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
种子粒数
100
400
800
1 000
2 000
5 000
发芽种子粒数
85
298
652
793
1 604
4 005
发芽频率
0.850
0.745
0.815
0.793
0.802
0.801
根据以上数据可以估计,该玉米种子发芽的概率约为 (精确到0.1).?
17.在一个不透明的空袋子里,放入仅颜色不同的2个红球和1个白球,从中随机摸出1个球后不放回,再从中随机摸出1个球,两次都摸到红球的概率是 .?
18.从-1,0,1,2这四个数中,任取两个不同的数作为点的坐标,则该点在第一象限的概率为 .?
19.如图,随机闭合开关S1,S2,S3中的两个,能让灯泡发光的概率是 .?
20.有两把不同的锁和三把钥匙,其中两把钥匙能打开同一把锁,第三把钥匙不能打开这两把锁,任取出一把钥匙去开任意的一把锁,一次打开锁的概率为 .?
三、解答题(本大题共7小题,共80分)
21.(8分)小明代表学校参加“我和我的祖国”主题宣传教育活动.该活动分为两个阶段,第一阶段有“歌曲演唱”“书法展示”“器乐独奏”3个项目(依次用A,B,C表示),第二阶段有“故事演讲”“诗歌朗诵”2个项目(依次用D,E表示),参加人员在每个阶段各随机抽取一个项目完成.用画树状图或列表的方法列出小明参加项目的所有等可能的结果,并求小明恰好抽中B,D两个项目的概率.
22.(8分)为增强学生的环保意识,某中学举办了环保知识竞赛,某班共有5名学生(3名男生、2名女生)获奖.
(1)老师若从获奖的5名学生中选取一名作为班级的“环保小卫士”,则恰好是男生的概率为 .?
(2)老师若从获奖的5名学生中任选两名作为班级的“环保小卫士”,请用画树状图法或列表法,求出恰好是一名男生、一名女生的概率.
23.(10分)阅读对话,解答问题:
(1)分别用a,b表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字,请用画树状图法或列表法写出(a,b)的所有取值.
(2)求在(a,b)中使关于x的一元二次方程x2-ax+2b=0有实数根的概率.
24.(12分)某校5月份举行了八年级生物实验考查,有A和B两个考查实验,规定每位学生只参加其中一个实验的考查,并由学生自己抽签决定具体的考查实验,小明、小丽、小华都参加了本次考查.
(1)小丽参加实验A考查的概率是 .?
(2)用列表或画树状图的方法求小明、小丽都参加实验A考查的概率.
(3)他们三人都参加实验A考查的概率是 .?
25.(12分)为了参加中考体育测试,甲、乙、丙三位同学进行足球传球训练.球从一个人脚下随机传到另一个人脚下,且每位传球人传球给其余两人的机会是均等的,由甲开始传球,共传三次.
(1)用树状图列举出三次传球的所有等可能情况.
(2)求传球三次后,球回到甲脚下的概率.
(3)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
26.(14分)在一个不透明的口袋里有分别标注2,4,6的3个小球(小球除数字不同外,其余都相同),另有3张背面完全一样、正面分别写有数字6,7,8的卡片.现从口袋中任意摸出一个小球,再从这3张背面朝上的卡片中任意摸出一张卡片.
(1)请你用列表或画树状图的方法,表示出所有等可能出现的结果.
(2)小红和小莉做游戏,制定了两个游戏规则:
规则1:若两次摸出的数字,至少有一次是“6”,小红赢;否则,小莉赢.
规则2:若摸出的卡片上的数字是球上数字的整数倍时,小红赢;否则,小莉赢.
小红要想在游戏中获胜,她会选择哪一种规则,并说明理由.
27.(16分)电子政务、数字经济、智慧社会…一场数字革命正在神州大地激荡.在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整):
“掌握新技术,走进数时代”信息技术
应用大赛成绩频数分布统计表 “掌握新技术,走进数时代”信息
技术应用大赛成绩扇形统计图
组别
成绩x(分)
人数
A
60≤x<70
10
B
70≤x<80
m
C
80≤x<90
16
D
90≤x≤100
4
请观察上面的图表,解答下列问题:
(1)统计表中m= ;统计图中n= ,D组的圆心角是 度.?
(2)D组的4名学生中,有2名男生和2名女生.从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法,求:
①恰好1名男生和1名女生被抽取参加5G体验活动的概率;
②至少1名女生被抽取参加5G体验活动的概率.
第三章过关与测试
1.D 2.A 3.D 4.C 5.B 6.B 7.C 8.B 9.B 10.D 11.C 12.A 13.A 14.C 15.B 16.0.8 17.13 18.16 19.23 20.13
21.解:画树状图如图所示.
由树状图知共有6种等可能结果,其中小明恰好抽中B,D两个项目的只有1种情况,
所以小明恰好抽中B,D两个项目的概率为16.
22.解:(1)由于5名学生中共有男生3名,所以抽到男生的概率为35,
故答案为35.
(2)画树状图为:
共有20种等可能的结果数,其中选出1名男生和1名女生的结果为12种,所以恰好选出1名男生和1名女生的概率为1220=35.
23.解:(1)(a,b)对应的表格为:
b
a
1
2
3
1
(1,1)
(1,2)
(1,3)
2
(2,1)
(2,2)
(2,3)
3
(3,1)
(3,2)
(3,3)
4
(4,1)
(4,2)
(4,3)
(2)∵方程x2-ax+2b=0有实数根,∴Δ=a2-8b≥0.
∴使a2-8b≥0的(a,b)有(3,1),(4,1),(4,2),
∴P(有实数根)=312=14.
24.解:(1)由于只有A和B两个考查实验,所以小丽参加实验A考查的概率是12,故答案为12.
(2)画树状图如图所示.∵两人参加的实验考查共有四种等可能结果,而两人均参加实验A考查有1种,∴小明、小丽都参加实验A考查的概率为14.
(3)由列表或画树状图可知,他们参加实验考查的情况共有8种,而他们均参加实验A考查的情况只有1种,所以他们三人都参加实验A考查的概率为18.故答案为18.
25.解:(1)三次传球所有等可能的情况如图:
(2)由上图知:三次传球后,球回到甲的概率为P(甲)=28=14.
(3)由上图知:三次传球后,球回到乙的概率为P(乙)=38,
P(乙)>P(甲),所以球传到乙脚下的概率要大.
26.解:(1)列表如下:
卡片
小球
6
7
8
2
(2,6)
(2,7)
(2,8)
4
(4,6)
(4,7)
(4,8)
6
(6,6)
(6,7)
(6,8)
画树状图如图所示:
共有9种等可能结果,分别是(2,6),(2,7),(2,8),(4,6),(4,7),(4,8),(6,6),(6,7),(6,8).
(2)从表格或树状图可知,至少有一次是“6”的情况有5种,所以,小红赢的概率是P(至少有一次是“6”)=59,小莉赢的概率是49,
∵59>49,∴此规则小红获胜的概率大.
卡片上的数字是球上数字的整数倍的有:(2,6),(2,8),(4,8),(6,6),共4种情况,所以,小红赢的概率是P(卡片上的数字是球上数字的整数倍)=49,小莉赢的概率是59,
∵59>49,∴此规则小莉获胜的概率大,
∴小红要想在游戏中获胜,她应该选择规则1.
27.解:(1)被调查的总人数为10÷20%=50,
则m=50-(10+16+4)=20,n%=1650×100%=32%,即n=32,
D组的圆心角是360°×450=28.8°.
(2)①设男同学标记为A,B;女学生标记为1,2,可能出现的所有结果列表如下:
A
B
1
2
A
/
(B,A)
(1,A)
(2,A)
B
(A,B)
/
(1,B)
(2,B)
1
(A,1)
(B,1)
/
(2,1)
2
(A,2)
(B,2)
(1,2)
/
共有12种等可能的结果,其中刚好抽到一男一女的结果有8种,
∴恰好1名男生和1名女生被抽取参加5G体验活动的概率为812=23;
②∵至少1名女生被抽取参加5G体验活动的有10种结果,
∴至少1名女生被抽取参加5G体验活动的概率为1012=56.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
