4.5.2 角的补(余)角 课件(共19张PPT)
文档属性
| 名称 | 4.5.2 角的补(余)角 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-28 14:15:18 | ||
图片预览






文档简介
(共19张PPT)
第2课时
角的补(余)角
沪科版
七年级数学上册
4.5
角的比较与补(余)角
学习目标
【知识与技能】
理解互补、互余的概念,并能利用补(余)角的性质解决问题.
【过程与方法】
从学生熟悉的角的比较和平分线中引出补(余)角的概念,并通过各种师生活动加深学生对补(余)角的概念的理解;经历概念的形成过程和性质的探究过程,培养观察、归纳、概括能力,发展几何直觉.
【情感态度】
通过实际观察、操作体会直角和平角,能用符号语言描述直角和平角,能运用互补(余)的性质解决实际问题.
【教学重点】
重点是理解互补(余)的性质.
【教学难点】
难点是认识角之间的关系.
新课导入
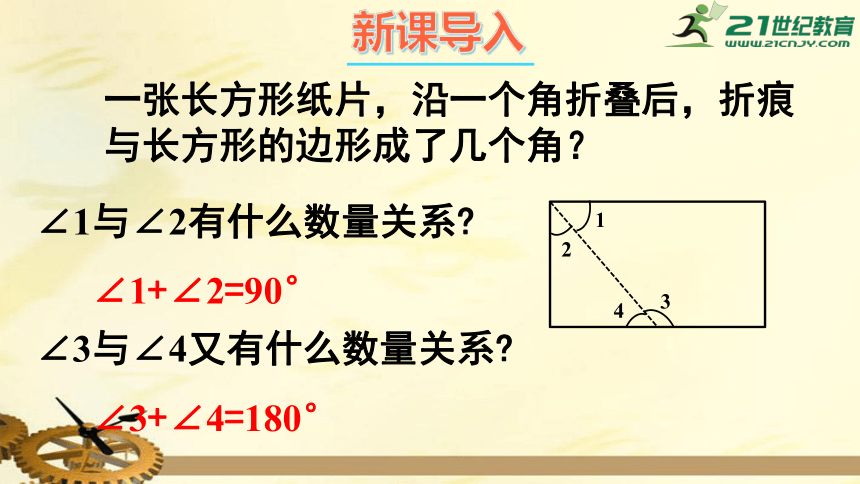
一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了几个角?
1
2
3
4
∠1与∠2有什么数量关系?
∠1+∠2=90°
∠3与∠4又有什么数量关系?
∠3+∠4=180°
如果两个角的和等于180?(平角),就说这两个角互为补角,即其中一个角是另一个角的补角,简称互补.
180°
如图,∠1+∠2=180°,∠1叫做∠2的补角,∠2也叫做∠1的补角,∠1与∠2互补.
2
1
90°
如果两个角的和等于90?(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角,简称互余.
β
α
如图,∠α+∠β=90°,∠α叫做∠β的余角,∠β叫做∠α的余角,∠α与∠β互余.
例
如图,∠1=∠3,∠1与∠2互补,∠3与∠4互补,那么∠2与∠4有什么关系?
2
1
4
3
解
因为∠1与∠2互补,
所以∠2=180°-∠1,
因为∠3与∠4互补,
所以∠4=180°-∠3
又
因为∠1=∠3
所以∠2=∠4.
补角的性质:同角(或等角)的补角相等
思
考
余角有无上面补角类似的性质?如果有,你能说明道理吗?
同角(或等角)的余角相等
练
习
已知:如图,点O为直线AB上一点,OC是∠AOB的平分线,OD在∠COB内.(选填“<”“>”或“=”):
O
A
B
C
D
O
A
B
C
D
(1)∠AOD
∠AOB,
∠AOD
∠DOB,
∠AOC
∠BOC;
(2)∠AOD的补角是
,
∠COD的余角是
,
∠BOD的补角是
,
∠AOC的补角是
.
<
>
=
∠BOD
∠BOD
∠AOD
∠BOC
随堂练习
1.下列说法不正确的是(
)
A.任意两直角互补
B.任意两锐角互余
C.同角或等角的补角相等
D.同角或等角的余角相等
B
2.下列结论正确的个数为(
)
①互余且相等的两个角都是45°
②锐角的补角一定是钝角
③一个角的补角一定大于这个角
④一个锐角的补角比这个角的余角大90°
A.1个
B.2个
C.3个
D.4个
C
3.如图,点O在直线PQ上,OA是∠QOB的平分线,OC是∠POB的平分线,那么下列说法错误的是(
)
A.∠AOB与∠POC互余
B.∠POC与∠QOA互余
C.∠POC与∠QOB互补
D.∠AOP与∠AOB互补
C
课后小结
等角
的余角相等.
等角
的补角相等.
(同角)
(同角)
1.从教材习题中选取.
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
第2课时
角的补(余)角
沪科版
七年级数学上册
4.5
角的比较与补(余)角
学习目标
【知识与技能】
理解互补、互余的概念,并能利用补(余)角的性质解决问题.
【过程与方法】
从学生熟悉的角的比较和平分线中引出补(余)角的概念,并通过各种师生活动加深学生对补(余)角的概念的理解;经历概念的形成过程和性质的探究过程,培养观察、归纳、概括能力,发展几何直觉.
【情感态度】
通过实际观察、操作体会直角和平角,能用符号语言描述直角和平角,能运用互补(余)的性质解决实际问题.
【教学重点】
重点是理解互补(余)的性质.
【教学难点】
难点是认识角之间的关系.
新课导入
一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了几个角?
1
2
3
4
∠1与∠2有什么数量关系?
∠1+∠2=90°
∠3与∠4又有什么数量关系?
∠3+∠4=180°
如果两个角的和等于180?(平角),就说这两个角互为补角,即其中一个角是另一个角的补角,简称互补.
180°
如图,∠1+∠2=180°,∠1叫做∠2的补角,∠2也叫做∠1的补角,∠1与∠2互补.
2
1
90°
如果两个角的和等于90?(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角,简称互余.
β
α
如图,∠α+∠β=90°,∠α叫做∠β的余角,∠β叫做∠α的余角,∠α与∠β互余.
例
如图,∠1=∠3,∠1与∠2互补,∠3与∠4互补,那么∠2与∠4有什么关系?
2
1
4
3
解
因为∠1与∠2互补,
所以∠2=180°-∠1,
因为∠3与∠4互补,
所以∠4=180°-∠3
又
因为∠1=∠3
所以∠2=∠4.
补角的性质:同角(或等角)的补角相等
思
考
余角有无上面补角类似的性质?如果有,你能说明道理吗?
同角(或等角)的余角相等
练
习
已知:如图,点O为直线AB上一点,OC是∠AOB的平分线,OD在∠COB内.(选填“<”“>”或“=”):
O
A
B
C
D
O
A
B
C
D
(1)∠AOD
∠AOB,
∠AOD
∠DOB,
∠AOC
∠BOC;
(2)∠AOD的补角是
,
∠COD的余角是
,
∠BOD的补角是
,
∠AOC的补角是
.
<
>
=
∠BOD
∠BOD
∠AOD
∠BOC
随堂练习
1.下列说法不正确的是(
)
A.任意两直角互补
B.任意两锐角互余
C.同角或等角的补角相等
D.同角或等角的余角相等
B
2.下列结论正确的个数为(
)
①互余且相等的两个角都是45°
②锐角的补角一定是钝角
③一个角的补角一定大于这个角
④一个锐角的补角比这个角的余角大90°
A.1个
B.2个
C.3个
D.4个
C
3.如图,点O在直线PQ上,OA是∠QOB的平分线,OC是∠POB的平分线,那么下列说法错误的是(
)
A.∠AOB与∠POC互余
B.∠POC与∠QOA互余
C.∠POC与∠QOB互补
D.∠AOP与∠AOB互补
C
课后小结
等角
的余角相等.
等角
的补角相等.
(同角)
(同角)
1.从教材习题中选取.
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
