4.3 线段的长短比较 课件(共20张PPT)
文档属性
| 名称 | 4.3 线段的长短比较 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-29 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
4.3
线段的长短比较
沪科版
七年级数学上册
学习目标
【知识与技能】
1.借助“比身高”的情景,了解比较线段长短的方法.
2.理解和掌握“两点之间的所有连线中线段最短”这一基本事实.
3.掌握线段的中点的概念,并能运用线段的中点解决问题.
4.通过实际问题的解决培养学生分析、判断和解决实际问题的能力.
【过程与方法】
从学生熟悉的线段的基础上,引出“线段的比较”的方法,并通过各种师生活动加深学生对“线段的中点”,“线段的基本事实和两点间的距离”的理解;使学生在经历学习线段比较的过程中,体会类比思想和归纳思想.
【情感态度】
从学生已有的知识中提出问题,既体现知识的连贯性,又体现知识的应用性,通过比较大小以及进行一些运算,使学生对几何图形与数之间的联系有一定的认识,从而初步了解数形结合的思想,培养学生的空间观念,同时还有利于激发学生的学习兴趣.
【教学重点】
重点是了解线段的比较方法,两点之间的距离和线段中点的概念.
【教学难点】
难点是比较线段长短的方法,线段中点的表示方法及应用.
思
考
怎样比较下列线段AB,CD的长短呢?
A
B
C
D
可以采用叠合法、度量法.
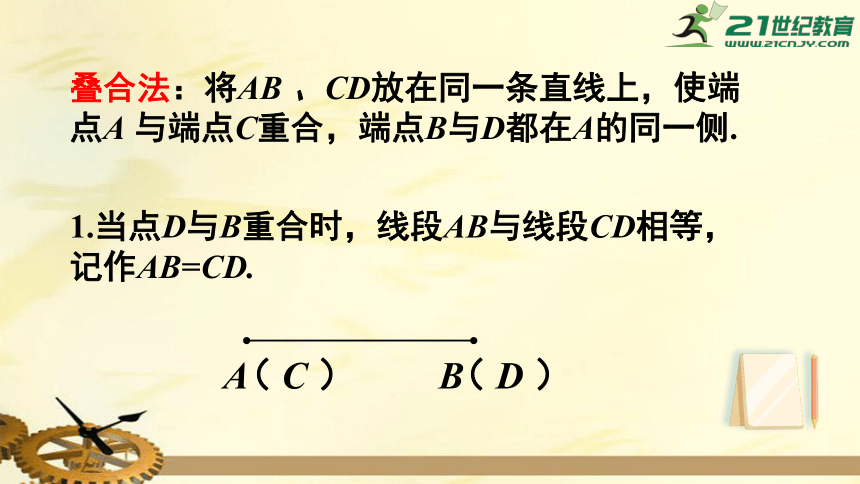
叠合法:将AB
、CD放在同一条直线上,使端点A
与端点C重合,端点B与D都在A的同一侧.
1.当点D与B重合时,线段AB与线段CD相等,记作AB=CD.
A
B
(
C
)
(
D
)
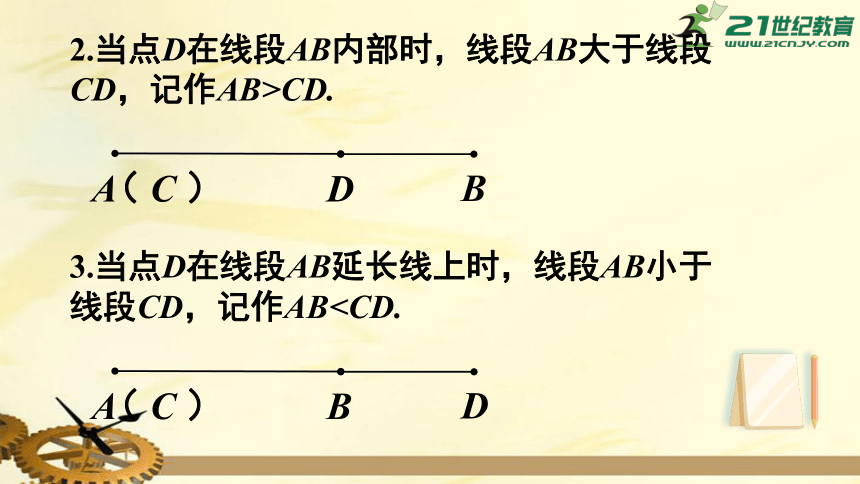
2.当点D在线段AB内部时,线段AB大于线段CD,记作AB>CD.
A
B
(
C
)
D
3.当点D在线段AB延长线上时,线段AB小于线段CD,记作ABA
D
(
C
)
B
度量法:我们也可以利用刻度尺量出线段
的长度,来比较它们的长短.
A
B
C
D
如图,已知线段
a
和
b,且
a>b.
a
b
a.
AB=a,BC=b,则线段AC就是a与b的
.
记作
.
A
B
C
和
AC=a+b
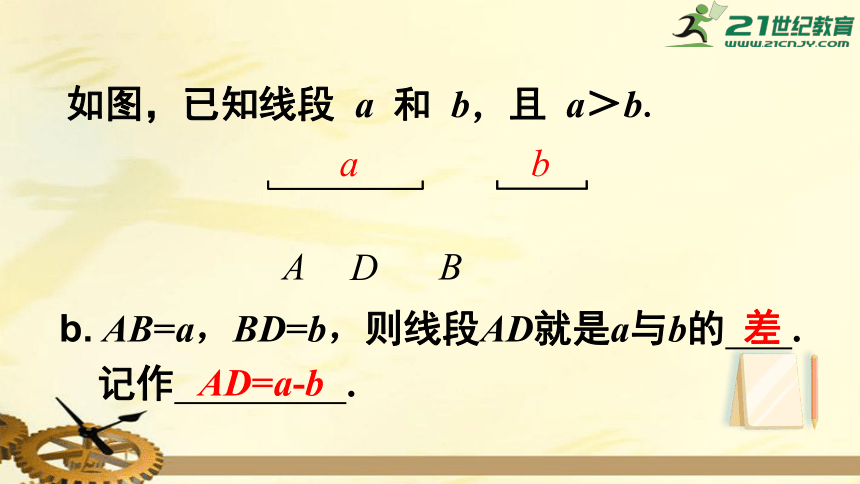
如图,已知线段
a
和
b,且
a>b.
a
b
b.
AB=a,BD=b,则线段AD就是a与b的
.
记作
.
A
B
差
AD=a-b
D
如图,点C在线段AB上且使线段AC,
CB相等,这样的点C叫做线段AB的中点.
这时有AC=CB=
AB,
或
AB=AC+CB=2AC=2CB
C
B
A
练
习
如图,甲、乙两地间有曲线、折线、线段等4条路线可走,其中哪一条路线最短?
甲
乙
线段有如下的基本事实:
两点之间的所有连线中,线段最短.
两点之间线段的长度,叫做这两点之间的距离.
例
已知:线段AB=4,延长AB至点C,使AC=11.点D是AB的中点,点E是AC的中点.求DE的长.
解
如图,因为AB=4,点D为AB中点,
故AD=2.
又
因为AC=11,点E为AC中点,AE=5.5
故DE=AE-AD=5.5-2=3.5.
E
C
A
D
B
随堂练习
1.如图,CB=
AB,AC=
AD,AB=
AE,若CB=2cm,则AE=(
)
A.6cm
B.8cm
C.10cm
D.12cm
D
2.下列说法中正确的是(
)
A.连结两点的线段叫做两点间的距离
B.在所有连接两点的线中,直线最短
C.线段AB就是表示点A到点B的距离
D.点A到点B的距离就是线段AB的长度
D
3.已知A、B、C三点在同一直线上,如果
线段AB=6cm,BC=3cm,A、C两点的
距离为d,那么(
)
A.d=9cm
B.d=3cm
C.d=9cm或d=3cm
D.d大小不确定
C
课后小结
线段的比较:叠合法、度量法
两点之间所有的连线中,线段最短.
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
4.3
线段的长短比较
沪科版
七年级数学上册
学习目标
【知识与技能】
1.借助“比身高”的情景,了解比较线段长短的方法.
2.理解和掌握“两点之间的所有连线中线段最短”这一基本事实.
3.掌握线段的中点的概念,并能运用线段的中点解决问题.
4.通过实际问题的解决培养学生分析、判断和解决实际问题的能力.
【过程与方法】
从学生熟悉的线段的基础上,引出“线段的比较”的方法,并通过各种师生活动加深学生对“线段的中点”,“线段的基本事实和两点间的距离”的理解;使学生在经历学习线段比较的过程中,体会类比思想和归纳思想.
【情感态度】
从学生已有的知识中提出问题,既体现知识的连贯性,又体现知识的应用性,通过比较大小以及进行一些运算,使学生对几何图形与数之间的联系有一定的认识,从而初步了解数形结合的思想,培养学生的空间观念,同时还有利于激发学生的学习兴趣.
【教学重点】
重点是了解线段的比较方法,两点之间的距离和线段中点的概念.
【教学难点】
难点是比较线段长短的方法,线段中点的表示方法及应用.
思
考
怎样比较下列线段AB,CD的长短呢?
A
B
C
D
可以采用叠合法、度量法.
叠合法:将AB
、CD放在同一条直线上,使端点A
与端点C重合,端点B与D都在A的同一侧.
1.当点D与B重合时,线段AB与线段CD相等,记作AB=CD.
A
B
(
C
)
(
D
)
2.当点D在线段AB内部时,线段AB大于线段CD,记作AB>CD.
A
B
(
C
)
D
3.当点D在线段AB延长线上时,线段AB小于线段CD,记作AB
D
(
C
)
B
度量法:我们也可以利用刻度尺量出线段
的长度,来比较它们的长短.
A
B
C
D
如图,已知线段
a
和
b,且
a>b.
a
b
a.
AB=a,BC=b,则线段AC就是a与b的
.
记作
.
A
B
C
和
AC=a+b
如图,已知线段
a
和
b,且
a>b.
a
b
b.
AB=a,BD=b,则线段AD就是a与b的
.
记作
.
A
B
差
AD=a-b
D
如图,点C在线段AB上且使线段AC,
CB相等,这样的点C叫做线段AB的中点.
这时有AC=CB=
AB,
或
AB=AC+CB=2AC=2CB
C
B
A
练
习
如图,甲、乙两地间有曲线、折线、线段等4条路线可走,其中哪一条路线最短?
甲
乙
线段有如下的基本事实:
两点之间的所有连线中,线段最短.
两点之间线段的长度,叫做这两点之间的距离.
例
已知:线段AB=4,延长AB至点C,使AC=11.点D是AB的中点,点E是AC的中点.求DE的长.
解
如图,因为AB=4,点D为AB中点,
故AD=2.
又
因为AC=11,点E为AC中点,AE=5.5
故DE=AE-AD=5.5-2=3.5.
E
C
A
D
B
随堂练习
1.如图,CB=
AB,AC=
AD,AB=
AE,若CB=2cm,则AE=(
)
A.6cm
B.8cm
C.10cm
D.12cm
D
2.下列说法中正确的是(
)
A.连结两点的线段叫做两点间的距离
B.在所有连接两点的线中,直线最短
C.线段AB就是表示点A到点B的距离
D.点A到点B的距离就是线段AB的长度
D
3.已知A、B、C三点在同一直线上,如果
线段AB=6cm,BC=3cm,A、C两点的
距离为d,那么(
)
A.d=9cm
B.d=3cm
C.d=9cm或d=3cm
D.d大小不确定
C
课后小结
线段的比较:叠合法、度量法
两点之间所有的连线中,线段最短.
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
