2020-2021学年度人教版小学五年级数学上册第七单元检测试题(含答案)
文档属性
| 名称 | 2020-2021学年度人教版小学五年级数学上册第七单元检测试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 189.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-28 00:00:00 | ||
图片预览




文档简介
2020-2021学年度人教版小学五年级数学上册第七单元检测试题(含答案)
一、填空题
1.把40个5用“+”相加,一共要_____个“+”.
2.有一根钢管,要锯成16小段,需要锯_____次.
3.在一条长40米的马路的一边,从头到尾每隔5米种一棵树,一共可以种______棵树。
4.两座楼房之间相隔60米,每隔3米栽一棵玉兰花(栽一排,两端都不栽),共栽了(_____)棵.
5.时钟4点钟敲4下,6秒敲完,那么8点钟敲8下,_____秒敲完.
6.一根木棒锯成4段要6分钟,锯成8段需要_____分钟.
7.在封闭的线路上植树,棵数=总距离÷间隔长._____
8.一个三角形花坛,每边放3盆花(每个角上放1盆),需要6盆花._____.
9.马路一边有一些电线杆,每两根电线杆中间有一个广告牌,已知广告牌有25个,那么电线杆有_____根.
10.你的左手有_____根手指,_____个间隔.
二、选择题
11.56人参加户外拓展训练,将22人安排在A营地,34人安排在B营地。从12:01开始,每逢整点A营地派出12人前往B营地,B营地派出8人前往A营地。已知两个营地之间的单程用时为30分钟,问以下哪个时间点,位于B营地的人数正好是A营地的3倍?( )
A.13:20 B.13:40 C.14:20 D.14:40
12.南岗中学每一位校长都是任职一届,一届任期三年,那么在8年期间南岗中学最多可能有几位校长?( )。
A.2 B.3 C.4 D.5
13.李先生去10层楼的8层去办事,恰赶上电梯停电,他只能步行爬楼。他从第1层爬到第4层用了48秒,请问,以同样的速度爬到第8层需要多少秒?( )。
A.112 B.96 C.64 D.48
14.邮递员每天要取6次信.第一次是早晨7时,最后一次是下午5时.如果取信的时间间隔相同,那么第四次取信是( )时.
A.9 B.11 C.13 D.15
15.把一根木棒截成二段要6分钟,照这样计算,如果要截成三段要用( )分钟.
A.6 B.8 C.9 D.12
三、判断题
16.两个面积相等的梯形一定可以拼成一个平行四边形。(______)
17.平行四边形面积是三角形面积的2倍. (________)
18.一根竹竿长4米.锯4次能把它锯成4小段_____.
19.小红从一楼到三楼需60秒,照这样的速度,如果小红从一楼走到十楼一共就要花200秒. .
20.时钟敲5下,用8秒钟,敲10下用18秒._____.
四、计算题
21.口算.
false false false false
false false false false
false false
22.用简便方法计算。
6.5×7.24-5.24×6.5 7.2×1.25 4.8×9.9
23.解下列方程.
35+x=87 6(2x-7)=54 3.4x+5.3x=20.01
58-3x=37 23.6x-22.2x=23.94 (4x-16)÷5=8.6
五、解答题
24.甲、乙两地相距20千米,每隔4千米设一个站牌,甲、乙两地之间一共设有多少个站牌?(甲、乙两地除外)
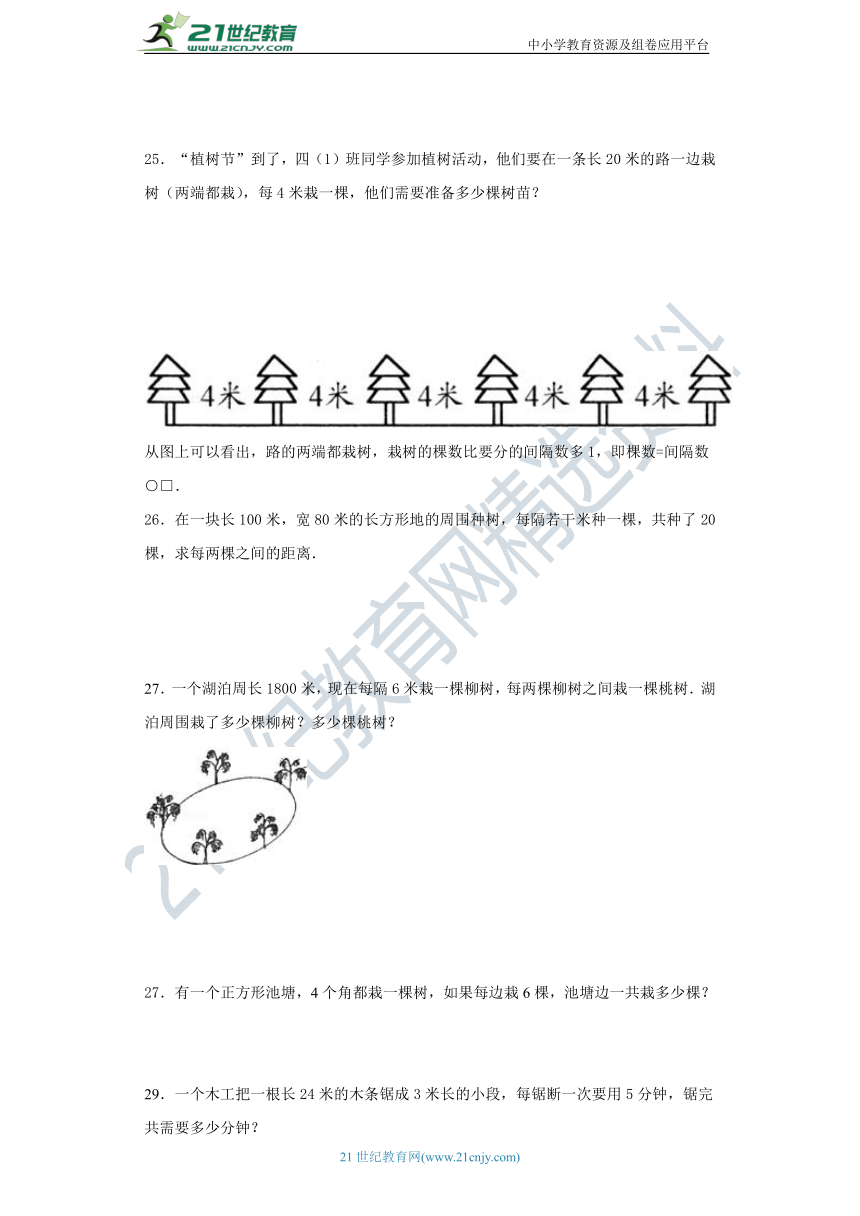
“植树节”到了,四(1)班同学参加植树活动,他们要在一条长20米的路一边栽树(两端都栽),每4米栽一棵,他们需要准备多少棵树苗?
从图上可以看出,路的两端都栽树,栽树的棵数比要分的间隔数多1,即棵数=间隔数○□.
在一块长100米,宽80米的长方形地的周围种树,每隔若干米种一棵,共种了20棵,求每两棵之间的距离.
27.一个湖泊周长1800米,现在每隔6米栽一棵柳树,每两棵柳树之间栽一棵桃树.湖泊周围栽了多少棵柳树?多少棵桃树?
有一个正方形池塘,4个角都栽一棵树,如果每边栽6棵,池塘边一共栽多少棵?
29.一个木工把一根长24米的木条锯成3米长的小段,每锯断一次要用5分钟,锯完共需要多少分钟?
参考答案
1.39
【解析】
【分析】
根据题意,两个5相加有一个“+”,三个5相加有2个“+”…,可以得出,“+”的个数比数的个数少1个,40个5相加,“+”的个数就是40﹣1=39个.
【详解】
40﹣1=39.
答:40个5用“+”相加,一共要39个“+”.
故答案为39.
2.15
【解析】
【分析】
把一根钢管锯成一样长的小段,锯了1次,则将这根钢管平均分成了1+1=2段,以此类推,锯的段数=锯的次数+1.要锯成16小段,需要锯16﹣1次,据此解答即可.
【详解】
16﹣1=15(次)
答:需要锯15次.
故答案为15.
3.6
【解析】
【分析】
树的间隔数为:40÷8=5个,由于两端都栽,所以一共栽了5+1=6棵;据此解答。
【详解】
40÷8+1
=5+1
=6(棵);
故答案为6。
【点睛】
本题考查了植树问题,知识点是:树的棵数=间隔数+1,间隔数=总长度÷间距;知识链接(沿直线上栽):栽树的棵数=间隔数﹣1(两端都不栽),植树的棵数=间隔数+1(两端都栽),植树的棵数=间隔数(只栽一端).
4.19
【解析】
【分析】
根据题意得出此题属于两端不栽树的问题,属于先求出60米里面有几个3米,再根据植树问题中两端不栽时植树棵数=间隔数﹣1,即可解答.
【详解】
60÷3﹣1
=20﹣1
=19(棵)
答:共栽了19棵.
故答案为19.
【点睛】
本题考查了植树问题中两端不栽时植树棵数=间隔数﹣1的计算应用.
5.14
【解析】
【分析】
敲4下,经过的时间间隔是:4﹣1=3个,共用了6秒钟,那么敲一次用:6÷3=2(秒);8点敲了8下,经过的时间间隔是:8﹣1=7个,共用了2×7=14秒钟,据此解答.
【详解】
6÷(4﹣1)×(8﹣1),
=2×7,
=14(秒);
答:14秒敲完.
故答案为14.
6.14
【解析】
【分析】
先明确锯4段需要锯3次,锯8段需要锯7次,根据锯成4段需要6分钟计算出锯1次需要几分钟,再计算出锯8段用的时间即可.
【详解】
锯1次的时间:6÷(4﹣1)=2(分钟),
锯8段需要的时间:2×(8﹣1)=14(分钟).
答:锯成8段需要14分钟.
故答案为14.
7.√
【解析】
【分析】
【详解】
由于在封闭的线路上植树,间隔数=树的棵数,而间隔数又等于总距离÷间隔长, 所以此题说法正确,
故答案为√.
8.正确
【解析】
【分析】
根据题干,用每边花盆数×3,因为每个顶点处的花盆重复相加了一次,所以再减去3即可.根据每边盆数×边数﹣顶点数,即可解答此类问题.
【详解】
3×3﹣3=6(盆),
答:需要6盆.
故答案为√.
9.26
【解析】
【分析】
本题考查了植树问题,知识点是:植树的棵数=间隔数+1(两端都栽).25根广告牌相当于25个间隔,那么电线杆有25+1=26(根).
【详解】
25+1=26(根);
答:电线杆有26根.
故答案为26.
10.5 4
【解析】
【分析】
把左手的5个手指看做5棵树,属于两端都要栽的情况,则间隔数=植树棵数﹣1,据此即可解答.
【详解】
左手有5根手指头,
所以5﹣1=4(个),
答:左手有5根手指头,有4个间隔.
11.D
【解析】
【分析】
根据题意,整点时,本营地人数派出人到对方营地,人数相对减少,但半点时,对方营地的人到达本营地,人数又相对增加,据此解答。
【详解】
A.13:20时,A营地派出12人前往B营地,B营地派出8人前往A营地,而对方营地派出的人还没有到达,这时A营地剩余22-12=10人,B营地剩余34-8=26人,不符合题意;
B.13:40时,两个营地各派出1次,且对方派出的人到达本营地,这时A营地有22-12+8=18人,B营地有34-8+12=38人,不符合题意;
C.14:20时,两个营地各派出两次,而第二次对方营地派出的人还没有到达,这时A营地有22-12+8-12=6人,B营地有34-8+12-8=30人,不符合题意;
D.14:40时,两个营地各派出两次,且对方派出的人到达本营地,这时A营地有22-12+8-12+8=14人,B营地有34-8+12-8+12=42人,42÷14=3,符合题意。
故答案为:D
【点睛】
整点到半点之前,对方派出的人未到达本营地,本营地人数相对减少;半点到下一个整点之前,对方营地派出的人到达本营地,本营地人数相对增加。
12.C
【解析】
【分析】
可从植树问题的角度来思考,本题属于两端植树的问题,计算8年有多少个间隔,再根据植树棵数=间隔数+1,计算出最多有多少位校长即可。
【详解】
8÷3≈3(个);
3+1=4(位);
故答案为:C。
【点睛】
明确本题可以用植树问题来解决,分清间隔数和植树棵数是解答本题的关键。
13.A
【解析】
【分析】
从1层爬到4层只需要爬4-1层楼,据此用时间÷层数,求出爬一层楼的时间,从1层爬到8层只需要爬8-1层楼,用爬一层楼的时间×到第8层需要爬的层数即可。
【详解】
48÷(4-1)×(8-1)
=48÷3×7
=112(秒)
故答案为:A
【点睛】
将第几层看成棵树,爬的层数看成段数,根据植树问题两头都植的方法去分析。
14.C
【解析】
【分析】
从早晨7时到下午5时,中间间隔10小时,此题相当于植树问题中的两端都要栽的问题:10小时之间的间隔数是6﹣1=5次,所以可得每隔10÷5=2小时就要取一次信,下午5时=17时,则第四次取信的时间是:17时﹣4时=13时.
【详解】
下午5时=17时,17时﹣7时=10时;
则第四次取信的时间是:
17﹣10÷(6﹣1)×2,
=17﹣2×2,
=17﹣4,
=13(时);
答:第4次取信的时刻是13时.
故选C.
15.D
【解析】
【分析】
根据题意,把一根木棒截成二段,只需要截一次,即每次截的时间是6分钟,如果要截成三段,要截3﹣1=2次,再乘上每次截的时间即可.
【详解】
每次截的时间是:(2﹣1)×6=6(分钟);
截成三段的时间是:(3﹣1)×6=12(分钟).
故选D.
16.×
【解析】
【分析】
两个完全相同的梯形才能拼成一个平行四边形,题干不能确定两个梯形是完全相同的,故不一定能拼成一个平行四边形。
【详解】
两个面积相等的梯形一定可以拼成一个平行四边形,因为未说明是形状相同,故无法判断,也可能不能拼成。
所以原题说法错误。
【点睛】
此题关键在于了解两个完全一样的梯形才能拼成平行四边形,只是面积相等是无法确定的。
17.×
【解析】
【分析】
【详解】
平行四边形的面积是与它等底等高的三角形面积的2倍.
18.×
【解析】
【分析】
根据题意,一根竹竿锯1次,可得到2小段,也就是说锯的次数加上1就是得到的段数,然后再进一步解答即可.
【详解】
锯4次,锯成的段数是:4+1=5(段);
所以,锯4次能把它锯成4小段是错误的.
故答案为×.
19.╳
【解析】
【分析】
根据“小红从一楼到三楼要用60秒,”知道小红走了(3﹣1)个楼梯间距用了60秒,由此求出走一个间距所用的时间;再根据“从一楼到十楼”,知道是走了(10﹣1)个间距,由此求出要求的答案.
【详解】
60÷(3﹣1)×(10﹣1),
=60÷2×9,
=30×9,
=270(秒);
答:用同样的速度从一楼到十楼用270秒.
故答案为×.
20.√
【解析】
【分析】
根据题意,时钟敲5下,有5﹣1=4个间隔,每个间隔的时间是8÷4=2秒;敲10下有10﹣1=9个间隔,用时9×2=18秒.然后再进一步解答.
【详解】
间隔时间:8÷(5﹣1)=2(秒);
敲10下用:(10﹣1)×2=18(秒).
故答案为√.
21.12;1;3.42;0.25
5.1;28;81;11.6
5;21.89
【解析】
【分析】
【详解】
小数乘法先按照整数方式计算,再看因数小数点后有几个数再带上小数的即可。小数的加减法注意数位的对齐,同样按照整数的计算理论即可,只不过小数点后的数位的意义略有差别而已。
【点睛】
掌握加减法数位对齐,同数位进行加减计算,乘除法可利用积和商的变化规律。
22.13;9;47.52
【解析】
【分析】
(1)根据乘法分配律的拓展来进行简算;
(2)将7.2分解成9×0.8,再将0.8按照乘法结合律,和1.25先算;
(3)将9.9分解成10-0.1,然后再利用乘法分配律进行简算。
【详解】
6.5×7.24-5.24×6.5
=6.5×(7.24-5.24)
=6.5×2
=13
7.2×1.25
=9×(0.8×1.25)
=9×1
=9
4.8×9.9
=4.8×(10-0.1)
=4.8×10-4.8×0.1
=48-0.48
=47.52
故答案为:13;9;47.52
【点睛】
本题根据小数的简便运算定律灵活选择来使得计算变得简便。
23.x=52;x=8;x=2.3
x=7;x=17.1;x=14.75
【解析】
【分析】
根据等式的性质,或者根据算式各部分之间的关系来解方程。
【详解】
35+x=87
解:35+x-35=87-35
x=52
6(2x-7)=54
解:6(2x-7)÷6=54÷6
2x-7+7=9+7
2x=16
x=8
3.4x+5.3x=20.01
解:8.7x=20.01
8.7x÷8.7=20.01÷8.7
x=2.3
58-3x=37
解:58-37=3x
3x=21
x=7
23.6x-22.2x=23.94
解:1.4x=23.94
1.2x÷1.4=23.94÷1.4
x=17.1
(4x-16)÷5=8.6
解:4x-16=8.6×5
4x-16+16=43+16
4x÷4=59÷4
x=14.75
故答案为:x=52;x=8;x=2.3
x=7;x=17.1;x=14.75
【点睛】
本题考查解方程的过程。
24.4个
【解析】
【分析】
本题考查了植树问题,知识点是:植树棵数=间隔数﹣1,间隔数=总距离÷间距;知识链接(沿直线上栽):栽树的棵数=间隔数﹣1(两端都不栽),植树的棵数=间隔数+1(两端都栽),植树的棵数=间隔数(只栽一端).先求出20千米里面有几个4千米,即有几个间隔,再减去1即可.
【详解】
20÷4﹣1
=5﹣1
=4(个)
答:需要设4个站牌.
25.6棵 +1
【解析】
【分析】
观察图形可知:两端都要栽时,植树棵数=间隔数+1,据此先求出20米中有几个4米,即得出一共有几个间隔,因为两端都要栽,所以用间隔数+1,即可得出植树棵数.
【详解】
20÷4+1=6(棵),
两端都要栽时,植树棵数=间隔数+1,
答:需要准备6棵树苗.路的两端都栽树,栽树的棵数比要分的间隔数多1,即棵数=间隔数+1.
26.18米
【解析】
【分析】
根据长方形的周长公式,求出长方形地的周围的米数,再根据整数除法的意义,即可求出每两棵树之间的距离.
【详解】
(100+80)×2÷20,
=180×2÷20,
=360÷20,
=18(米);
答:每两棵树之间的距离是18米.
27.300棵 300棵
【解析】
【分析】
(1)围成一个圆圈植树时:植树棵树=间隔数,由此先求出间隔数,从而得出柳树的棵数;
(2)由上面求出的间隔数×1就是栽种的桃树棵数.
【详解】
柳树有:1800÷6=300(棵),
桃树有300×1=300(棵),
答:沿湖周围栽了300棵柳树和300棵桃树.
28.20棵.
【解析】
【分析】
根据题意,在一个正方形池塘栽树,每边栽6棵,乘上边数4,即,6×4=24棵,因为4个角都栽一棵树,每个角的树都多数了一次,再减去4即可.
【详解】
根据题意可得:
6×4﹣4,
=24﹣4,
=20(棵).
答:塘边一共栽了20棵.
【点睛】
在封闭的正方形中栽树,四个角不栽树,栽树棵数=每边栽树棵数×边数4;四个角栽树,栽树棵数=每边栽树棵数×边数4﹣4.
29.35分钟
【解析】
【分析】
每3米锯一段,则可以锯成24÷3=8段;锯成8段,锯的次数是:8﹣1=7次,所以锯木用的时间是:7×5=35分钟;据此解答.
【详解】
(24÷3﹣1)×5,
=7×5,
=35(分钟),
答:锯完需要35分钟.
一、填空题
1.把40个5用“+”相加,一共要_____个“+”.
2.有一根钢管,要锯成16小段,需要锯_____次.
3.在一条长40米的马路的一边,从头到尾每隔5米种一棵树,一共可以种______棵树。
4.两座楼房之间相隔60米,每隔3米栽一棵玉兰花(栽一排,两端都不栽),共栽了(_____)棵.
5.时钟4点钟敲4下,6秒敲完,那么8点钟敲8下,_____秒敲完.
6.一根木棒锯成4段要6分钟,锯成8段需要_____分钟.
7.在封闭的线路上植树,棵数=总距离÷间隔长._____
8.一个三角形花坛,每边放3盆花(每个角上放1盆),需要6盆花._____.
9.马路一边有一些电线杆,每两根电线杆中间有一个广告牌,已知广告牌有25个,那么电线杆有_____根.
10.你的左手有_____根手指,_____个间隔.
二、选择题
11.56人参加户外拓展训练,将22人安排在A营地,34人安排在B营地。从12:01开始,每逢整点A营地派出12人前往B营地,B营地派出8人前往A营地。已知两个营地之间的单程用时为30分钟,问以下哪个时间点,位于B营地的人数正好是A营地的3倍?( )
A.13:20 B.13:40 C.14:20 D.14:40
12.南岗中学每一位校长都是任职一届,一届任期三年,那么在8年期间南岗中学最多可能有几位校长?( )。
A.2 B.3 C.4 D.5
13.李先生去10层楼的8层去办事,恰赶上电梯停电,他只能步行爬楼。他从第1层爬到第4层用了48秒,请问,以同样的速度爬到第8层需要多少秒?( )。
A.112 B.96 C.64 D.48
14.邮递员每天要取6次信.第一次是早晨7时,最后一次是下午5时.如果取信的时间间隔相同,那么第四次取信是( )时.
A.9 B.11 C.13 D.15
15.把一根木棒截成二段要6分钟,照这样计算,如果要截成三段要用( )分钟.
A.6 B.8 C.9 D.12
三、判断题
16.两个面积相等的梯形一定可以拼成一个平行四边形。(______)
17.平行四边形面积是三角形面积的2倍. (________)
18.一根竹竿长4米.锯4次能把它锯成4小段_____.
19.小红从一楼到三楼需60秒,照这样的速度,如果小红从一楼走到十楼一共就要花200秒. .
20.时钟敲5下,用8秒钟,敲10下用18秒._____.
四、计算题
21.口算.
false false false false
false false false false
false false
22.用简便方法计算。
6.5×7.24-5.24×6.5 7.2×1.25 4.8×9.9
23.解下列方程.
35+x=87 6(2x-7)=54 3.4x+5.3x=20.01
58-3x=37 23.6x-22.2x=23.94 (4x-16)÷5=8.6
五、解答题
24.甲、乙两地相距20千米,每隔4千米设一个站牌,甲、乙两地之间一共设有多少个站牌?(甲、乙两地除外)
“植树节”到了,四(1)班同学参加植树活动,他们要在一条长20米的路一边栽树(两端都栽),每4米栽一棵,他们需要准备多少棵树苗?
从图上可以看出,路的两端都栽树,栽树的棵数比要分的间隔数多1,即棵数=间隔数○□.
在一块长100米,宽80米的长方形地的周围种树,每隔若干米种一棵,共种了20棵,求每两棵之间的距离.
27.一个湖泊周长1800米,现在每隔6米栽一棵柳树,每两棵柳树之间栽一棵桃树.湖泊周围栽了多少棵柳树?多少棵桃树?
有一个正方形池塘,4个角都栽一棵树,如果每边栽6棵,池塘边一共栽多少棵?
29.一个木工把一根长24米的木条锯成3米长的小段,每锯断一次要用5分钟,锯完共需要多少分钟?
参考答案
1.39
【解析】
【分析】
根据题意,两个5相加有一个“+”,三个5相加有2个“+”…,可以得出,“+”的个数比数的个数少1个,40个5相加,“+”的个数就是40﹣1=39个.
【详解】
40﹣1=39.
答:40个5用“+”相加,一共要39个“+”.
故答案为39.
2.15
【解析】
【分析】
把一根钢管锯成一样长的小段,锯了1次,则将这根钢管平均分成了1+1=2段,以此类推,锯的段数=锯的次数+1.要锯成16小段,需要锯16﹣1次,据此解答即可.
【详解】
16﹣1=15(次)
答:需要锯15次.
故答案为15.
3.6
【解析】
【分析】
树的间隔数为:40÷8=5个,由于两端都栽,所以一共栽了5+1=6棵;据此解答。
【详解】
40÷8+1
=5+1
=6(棵);
故答案为6。
【点睛】
本题考查了植树问题,知识点是:树的棵数=间隔数+1,间隔数=总长度÷间距;知识链接(沿直线上栽):栽树的棵数=间隔数﹣1(两端都不栽),植树的棵数=间隔数+1(两端都栽),植树的棵数=间隔数(只栽一端).
4.19
【解析】
【分析】
根据题意得出此题属于两端不栽树的问题,属于先求出60米里面有几个3米,再根据植树问题中两端不栽时植树棵数=间隔数﹣1,即可解答.
【详解】
60÷3﹣1
=20﹣1
=19(棵)
答:共栽了19棵.
故答案为19.
【点睛】
本题考查了植树问题中两端不栽时植树棵数=间隔数﹣1的计算应用.
5.14
【解析】
【分析】
敲4下,经过的时间间隔是:4﹣1=3个,共用了6秒钟,那么敲一次用:6÷3=2(秒);8点敲了8下,经过的时间间隔是:8﹣1=7个,共用了2×7=14秒钟,据此解答.
【详解】
6÷(4﹣1)×(8﹣1),
=2×7,
=14(秒);
答:14秒敲完.
故答案为14.
6.14
【解析】
【分析】
先明确锯4段需要锯3次,锯8段需要锯7次,根据锯成4段需要6分钟计算出锯1次需要几分钟,再计算出锯8段用的时间即可.
【详解】
锯1次的时间:6÷(4﹣1)=2(分钟),
锯8段需要的时间:2×(8﹣1)=14(分钟).
答:锯成8段需要14分钟.
故答案为14.
7.√
【解析】
【分析】
【详解】
由于在封闭的线路上植树,间隔数=树的棵数,而间隔数又等于总距离÷间隔长, 所以此题说法正确,
故答案为√.
8.正确
【解析】
【分析】
根据题干,用每边花盆数×3,因为每个顶点处的花盆重复相加了一次,所以再减去3即可.根据每边盆数×边数﹣顶点数,即可解答此类问题.
【详解】
3×3﹣3=6(盆),
答:需要6盆.
故答案为√.
9.26
【解析】
【分析】
本题考查了植树问题,知识点是:植树的棵数=间隔数+1(两端都栽).25根广告牌相当于25个间隔,那么电线杆有25+1=26(根).
【详解】
25+1=26(根);
答:电线杆有26根.
故答案为26.
10.5 4
【解析】
【分析】
把左手的5个手指看做5棵树,属于两端都要栽的情况,则间隔数=植树棵数﹣1,据此即可解答.
【详解】
左手有5根手指头,
所以5﹣1=4(个),
答:左手有5根手指头,有4个间隔.
11.D
【解析】
【分析】
根据题意,整点时,本营地人数派出人到对方营地,人数相对减少,但半点时,对方营地的人到达本营地,人数又相对增加,据此解答。
【详解】
A.13:20时,A营地派出12人前往B营地,B营地派出8人前往A营地,而对方营地派出的人还没有到达,这时A营地剩余22-12=10人,B营地剩余34-8=26人,不符合题意;
B.13:40时,两个营地各派出1次,且对方派出的人到达本营地,这时A营地有22-12+8=18人,B营地有34-8+12=38人,不符合题意;
C.14:20时,两个营地各派出两次,而第二次对方营地派出的人还没有到达,这时A营地有22-12+8-12=6人,B营地有34-8+12-8=30人,不符合题意;
D.14:40时,两个营地各派出两次,且对方派出的人到达本营地,这时A营地有22-12+8-12+8=14人,B营地有34-8+12-8+12=42人,42÷14=3,符合题意。
故答案为:D
【点睛】
整点到半点之前,对方派出的人未到达本营地,本营地人数相对减少;半点到下一个整点之前,对方营地派出的人到达本营地,本营地人数相对增加。
12.C
【解析】
【分析】
可从植树问题的角度来思考,本题属于两端植树的问题,计算8年有多少个间隔,再根据植树棵数=间隔数+1,计算出最多有多少位校长即可。
【详解】
8÷3≈3(个);
3+1=4(位);
故答案为:C。
【点睛】
明确本题可以用植树问题来解决,分清间隔数和植树棵数是解答本题的关键。
13.A
【解析】
【分析】
从1层爬到4层只需要爬4-1层楼,据此用时间÷层数,求出爬一层楼的时间,从1层爬到8层只需要爬8-1层楼,用爬一层楼的时间×到第8层需要爬的层数即可。
【详解】
48÷(4-1)×(8-1)
=48÷3×7
=112(秒)
故答案为:A
【点睛】
将第几层看成棵树,爬的层数看成段数,根据植树问题两头都植的方法去分析。
14.C
【解析】
【分析】
从早晨7时到下午5时,中间间隔10小时,此题相当于植树问题中的两端都要栽的问题:10小时之间的间隔数是6﹣1=5次,所以可得每隔10÷5=2小时就要取一次信,下午5时=17时,则第四次取信的时间是:17时﹣4时=13时.
【详解】
下午5时=17时,17时﹣7时=10时;
则第四次取信的时间是:
17﹣10÷(6﹣1)×2,
=17﹣2×2,
=17﹣4,
=13(时);
答:第4次取信的时刻是13时.
故选C.
15.D
【解析】
【分析】
根据题意,把一根木棒截成二段,只需要截一次,即每次截的时间是6分钟,如果要截成三段,要截3﹣1=2次,再乘上每次截的时间即可.
【详解】
每次截的时间是:(2﹣1)×6=6(分钟);
截成三段的时间是:(3﹣1)×6=12(分钟).
故选D.
16.×
【解析】
【分析】
两个完全相同的梯形才能拼成一个平行四边形,题干不能确定两个梯形是完全相同的,故不一定能拼成一个平行四边形。
【详解】
两个面积相等的梯形一定可以拼成一个平行四边形,因为未说明是形状相同,故无法判断,也可能不能拼成。
所以原题说法错误。
【点睛】
此题关键在于了解两个完全一样的梯形才能拼成平行四边形,只是面积相等是无法确定的。
17.×
【解析】
【分析】
【详解】
平行四边形的面积是与它等底等高的三角形面积的2倍.
18.×
【解析】
【分析】
根据题意,一根竹竿锯1次,可得到2小段,也就是说锯的次数加上1就是得到的段数,然后再进一步解答即可.
【详解】
锯4次,锯成的段数是:4+1=5(段);
所以,锯4次能把它锯成4小段是错误的.
故答案为×.
19.╳
【解析】
【分析】
根据“小红从一楼到三楼要用60秒,”知道小红走了(3﹣1)个楼梯间距用了60秒,由此求出走一个间距所用的时间;再根据“从一楼到十楼”,知道是走了(10﹣1)个间距,由此求出要求的答案.
【详解】
60÷(3﹣1)×(10﹣1),
=60÷2×9,
=30×9,
=270(秒);
答:用同样的速度从一楼到十楼用270秒.
故答案为×.
20.√
【解析】
【分析】
根据题意,时钟敲5下,有5﹣1=4个间隔,每个间隔的时间是8÷4=2秒;敲10下有10﹣1=9个间隔,用时9×2=18秒.然后再进一步解答.
【详解】
间隔时间:8÷(5﹣1)=2(秒);
敲10下用:(10﹣1)×2=18(秒).
故答案为√.
21.12;1;3.42;0.25
5.1;28;81;11.6
5;21.89
【解析】
【分析】
【详解】
小数乘法先按照整数方式计算,再看因数小数点后有几个数再带上小数的即可。小数的加减法注意数位的对齐,同样按照整数的计算理论即可,只不过小数点后的数位的意义略有差别而已。
【点睛】
掌握加减法数位对齐,同数位进行加减计算,乘除法可利用积和商的变化规律。
22.13;9;47.52
【解析】
【分析】
(1)根据乘法分配律的拓展来进行简算;
(2)将7.2分解成9×0.8,再将0.8按照乘法结合律,和1.25先算;
(3)将9.9分解成10-0.1,然后再利用乘法分配律进行简算。
【详解】
6.5×7.24-5.24×6.5
=6.5×(7.24-5.24)
=6.5×2
=13
7.2×1.25
=9×(0.8×1.25)
=9×1
=9
4.8×9.9
=4.8×(10-0.1)
=4.8×10-4.8×0.1
=48-0.48
=47.52
故答案为:13;9;47.52
【点睛】
本题根据小数的简便运算定律灵活选择来使得计算变得简便。
23.x=52;x=8;x=2.3
x=7;x=17.1;x=14.75
【解析】
【分析】
根据等式的性质,或者根据算式各部分之间的关系来解方程。
【详解】
35+x=87
解:35+x-35=87-35
x=52
6(2x-7)=54
解:6(2x-7)÷6=54÷6
2x-7+7=9+7
2x=16
x=8
3.4x+5.3x=20.01
解:8.7x=20.01
8.7x÷8.7=20.01÷8.7
x=2.3
58-3x=37
解:58-37=3x
3x=21
x=7
23.6x-22.2x=23.94
解:1.4x=23.94
1.2x÷1.4=23.94÷1.4
x=17.1
(4x-16)÷5=8.6
解:4x-16=8.6×5
4x-16+16=43+16
4x÷4=59÷4
x=14.75
故答案为:x=52;x=8;x=2.3
x=7;x=17.1;x=14.75
【点睛】
本题考查解方程的过程。
24.4个
【解析】
【分析】
本题考查了植树问题,知识点是:植树棵数=间隔数﹣1,间隔数=总距离÷间距;知识链接(沿直线上栽):栽树的棵数=间隔数﹣1(两端都不栽),植树的棵数=间隔数+1(两端都栽),植树的棵数=间隔数(只栽一端).先求出20千米里面有几个4千米,即有几个间隔,再减去1即可.
【详解】
20÷4﹣1
=5﹣1
=4(个)
答:需要设4个站牌.
25.6棵 +1
【解析】
【分析】
观察图形可知:两端都要栽时,植树棵数=间隔数+1,据此先求出20米中有几个4米,即得出一共有几个间隔,因为两端都要栽,所以用间隔数+1,即可得出植树棵数.
【详解】
20÷4+1=6(棵),
两端都要栽时,植树棵数=间隔数+1,
答:需要准备6棵树苗.路的两端都栽树,栽树的棵数比要分的间隔数多1,即棵数=间隔数+1.
26.18米
【解析】
【分析】
根据长方形的周长公式,求出长方形地的周围的米数,再根据整数除法的意义,即可求出每两棵树之间的距离.
【详解】
(100+80)×2÷20,
=180×2÷20,
=360÷20,
=18(米);
答:每两棵树之间的距离是18米.
27.300棵 300棵
【解析】
【分析】
(1)围成一个圆圈植树时:植树棵树=间隔数,由此先求出间隔数,从而得出柳树的棵数;
(2)由上面求出的间隔数×1就是栽种的桃树棵数.
【详解】
柳树有:1800÷6=300(棵),
桃树有300×1=300(棵),
答:沿湖周围栽了300棵柳树和300棵桃树.
28.20棵.
【解析】
【分析】
根据题意,在一个正方形池塘栽树,每边栽6棵,乘上边数4,即,6×4=24棵,因为4个角都栽一棵树,每个角的树都多数了一次,再减去4即可.
【详解】
根据题意可得:
6×4﹣4,
=24﹣4,
=20(棵).
答:塘边一共栽了20棵.
【点睛】
在封闭的正方形中栽树,四个角不栽树,栽树棵数=每边栽树棵数×边数4;四个角栽树,栽树棵数=每边栽树棵数×边数4﹣4.
29.35分钟
【解析】
【分析】
每3米锯一段,则可以锯成24÷3=8段;锯成8段,锯的次数是:8﹣1=7次,所以锯木用的时间是:7×5=35分钟;据此解答.
【详解】
(24÷3﹣1)×5,
=7×5,
=35(分钟),
答:锯完需要35分钟.
