3.1不等关系与不等式
图片预览




文档简介
(共15张PPT)
一、新课引入
现实世界和日常生活中,既有相等关系,又存在着大量的不等关系,如:
1、今天的天气预报说:明天早晨最低温度为9℃,明天白天的最高温度为15℃;
2、三角形ABC的两边之和大于第三边;
3、a是一个非负实数。
在数学中,我们怎样来表示这些不等关系?
9℃≤t≤15℃
AB+AC>BC或……
a≥0
4、右图是限速40km/h的路标,指示司机在前方路段行驶时,应使汽车的速度v不超过40km/h ,写成不等式是:_________
40
5、某品牌酸奶的质量检查规定,酸奶中脂肪的含量f应不少于2.5%,蛋白质的含量p应不少于2.3%,用不等式可以表示为:( )
v≤40
A.f ≥ 2.5%或p ≥ 2.3%
B.f ≥ 2.5%且p ≥ 2.3%
C.
练习:用不等式表示下面的不等关系:
1、a与b的和是非负数;
2、某公路立交桥对通过车辆的高度h“限高4m”
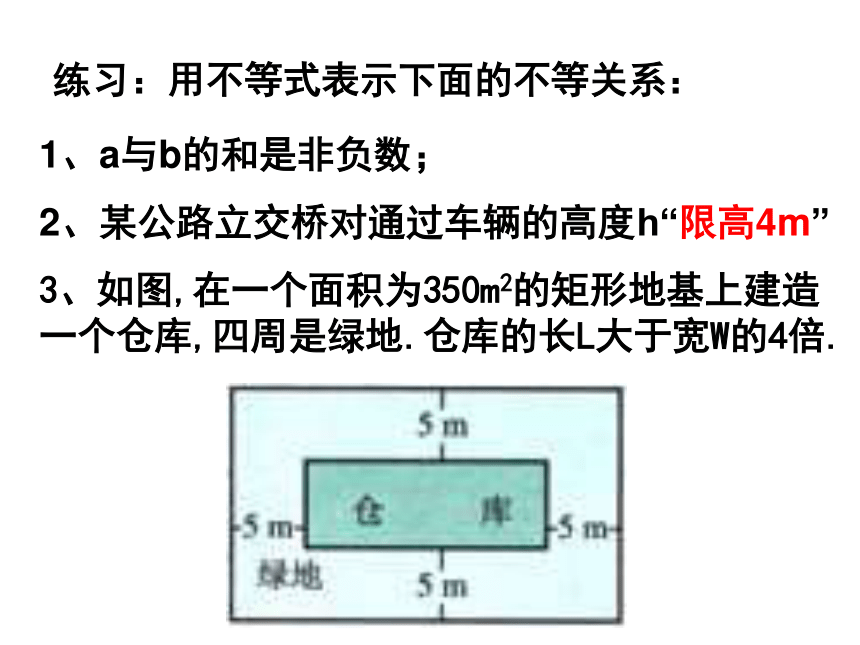
3、如图,在一个面积为350m2的矩形地基上建造
一个仓库,四周是绿地.仓库的长L大于宽W的4倍.
想一想,你还能举出哪些相似的例子
用不等式来解决生活中的不等关系问题:
问题1、某种杂志原以每本2.5元的价格销售,可以售出8万本。据市场调查,若单价每提高0.1元销售量就可能相应减少2000本。若把提价后杂志的定价设为x元,怎样用不等式表示销售的总收入仍不低于20万元呢?
变式: 如果设杂志的单价提高了0.1n元(n∈N*),如何用不等式表示销售的总收入
仍不低于20万元呢?
问题2、某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格。按照生产的要求,600mm的钢管的数量不能超过500mm钢管的3倍。怎样写出满足上述所有不等关系的不等式呢?
分析:假设截得500mm的钢管x根,截得600mm的钢管y根。
(3)截得两种钢管的数量都不能为负。
(2)截得600mm钢管的数量不能超过500mm的钢管数量的3倍;
(1)截得两种钢管的总长度不能超过4000mm;
根据题意,应当有什么样的不等关系呢?
练习1:若需在长为4000mm圆钢上,截出长为698mm和518mm的两种毛坯,问怎样写出满足上述所有不等关系的不等式组?
分析:设698mm与518mm分别x与y个
练习2、某年夏天,我国遭受特大洪灾,灾区学生小李家中经济发生困难,为帮助小李解决开学费用问题,小李所在班级学生(小李除外)决定承担这笔费用。若每人承担12元人民币,则多余84元;若每人承担10元,则不够;若每人承担11元,又多出40元以上。问该班共有多少人?这笔开学费用共多少元?
分析:设该班除小李外共有x人,这笔开学费用共y元,则:
客观事实:
(作差比较法的原理)
!
作差
变形
判断
结论
作差比较法的步骤:
因式分解、配方、通分等手段
三、课堂小结
本节课我们巩固了初中所学的二元一次不等式及二元一次不等式组,并且用它来解决现实生活中存在的大量不等关系的实际问题。
用不等式或不等式组表示实际问题中的不等关系时,思维要严密、规范。
一、新课引入
现实世界和日常生活中,既有相等关系,又存在着大量的不等关系,如:
1、今天的天气预报说:明天早晨最低温度为9℃,明天白天的最高温度为15℃;
2、三角形ABC的两边之和大于第三边;
3、a是一个非负实数。
在数学中,我们怎样来表示这些不等关系?
9℃≤t≤15℃
AB+AC>BC或……
a≥0
4、右图是限速40km/h的路标,指示司机在前方路段行驶时,应使汽车的速度v不超过40km/h ,写成不等式是:_________
40
5、某品牌酸奶的质量检查规定,酸奶中脂肪的含量f应不少于2.5%,蛋白质的含量p应不少于2.3%,用不等式可以表示为:( )
v≤40
A.f ≥ 2.5%或p ≥ 2.3%
B.f ≥ 2.5%且p ≥ 2.3%
C.
练习:用不等式表示下面的不等关系:
1、a与b的和是非负数;
2、某公路立交桥对通过车辆的高度h“限高4m”
3、如图,在一个面积为350m2的矩形地基上建造
一个仓库,四周是绿地.仓库的长L大于宽W的4倍.
想一想,你还能举出哪些相似的例子
用不等式来解决生活中的不等关系问题:
问题1、某种杂志原以每本2.5元的价格销售,可以售出8万本。据市场调查,若单价每提高0.1元销售量就可能相应减少2000本。若把提价后杂志的定价设为x元,怎样用不等式表示销售的总收入仍不低于20万元呢?
变式: 如果设杂志的单价提高了0.1n元(n∈N*),如何用不等式表示销售的总收入
仍不低于20万元呢?
问题2、某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格。按照生产的要求,600mm的钢管的数量不能超过500mm钢管的3倍。怎样写出满足上述所有不等关系的不等式呢?
分析:假设截得500mm的钢管x根,截得600mm的钢管y根。
(3)截得两种钢管的数量都不能为负。
(2)截得600mm钢管的数量不能超过500mm的钢管数量的3倍;
(1)截得两种钢管的总长度不能超过4000mm;
根据题意,应当有什么样的不等关系呢?
练习1:若需在长为4000mm圆钢上,截出长为698mm和518mm的两种毛坯,问怎样写出满足上述所有不等关系的不等式组?
分析:设698mm与518mm分别x与y个
练习2、某年夏天,我国遭受特大洪灾,灾区学生小李家中经济发生困难,为帮助小李解决开学费用问题,小李所在班级学生(小李除外)决定承担这笔费用。若每人承担12元人民币,则多余84元;若每人承担10元,则不够;若每人承担11元,又多出40元以上。问该班共有多少人?这笔开学费用共多少元?
分析:设该班除小李外共有x人,这笔开学费用共y元,则:
客观事实:
(作差比较法的原理)
!
作差
变形
判断
结论
作差比较法的步骤:
因式分解、配方、通分等手段
三、课堂小结
本节课我们巩固了初中所学的二元一次不等式及二元一次不等式组,并且用它来解决现实生活中存在的大量不等关系的实际问题。
用不等式或不等式组表示实际问题中的不等关系时,思维要严密、规范。
