3.3二元一次不等式(组)与简单的线性
文档属性
| 名称 | 3.3二元一次不等式(组)与简单的线性 |  | |
| 格式 | rar | ||
| 文件大小 | 125.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-11 08:10:20 | ||
图片预览





文档简介
(共21张PPT)
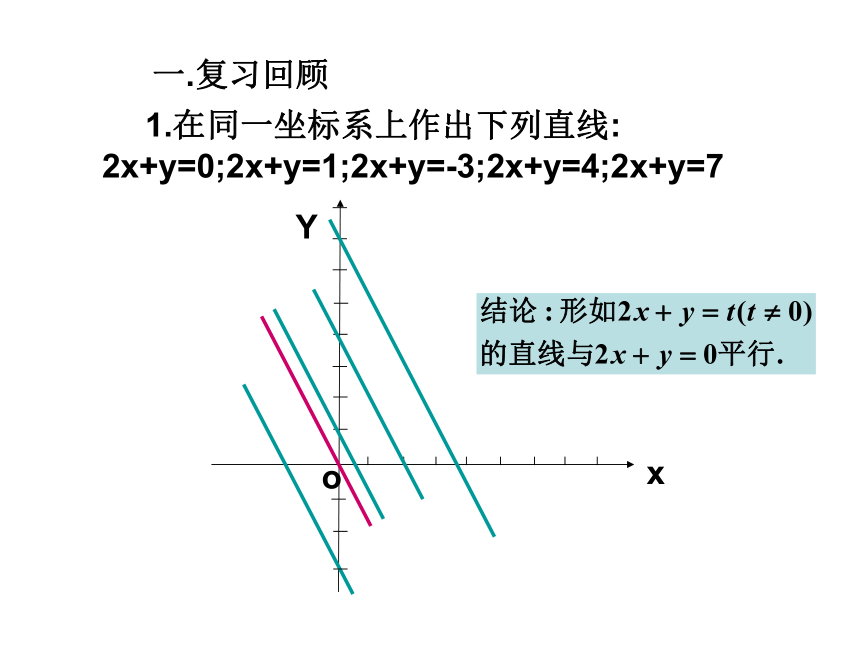
一.复习回顾
1.在同一坐标系上作出下列直线:
2x+y=0;2x+y=1;2x+y=-3;2x+y=4;2x+y=7
x
Y
o
2.作出下列不等式组所表示的平面区域
5
5
x=1
x-4y+3=0
3x+5y-25=0
1
A
B
C
C:
(1.00, 4.40)
A:
(5.00, 2.00)
B:
(1.00, 1.00)
O
x
y
问题1:x 有无最大(小)值?
问题2:y 有无最大(小)值?
问题3:2x+y 有无最大(小)值?
二.提出问题
把上面两个问题综合起来:
设z=2x+y,求满足
时,求z的最大值和最小值.
5
5
x=1
x-4y+3=0
3x+5y-25=0
1
A
B
C
C:
(1.00, 4.40)
A:
(5.00, 2.00)
B:
(1.00, 1.00)
O
x
y
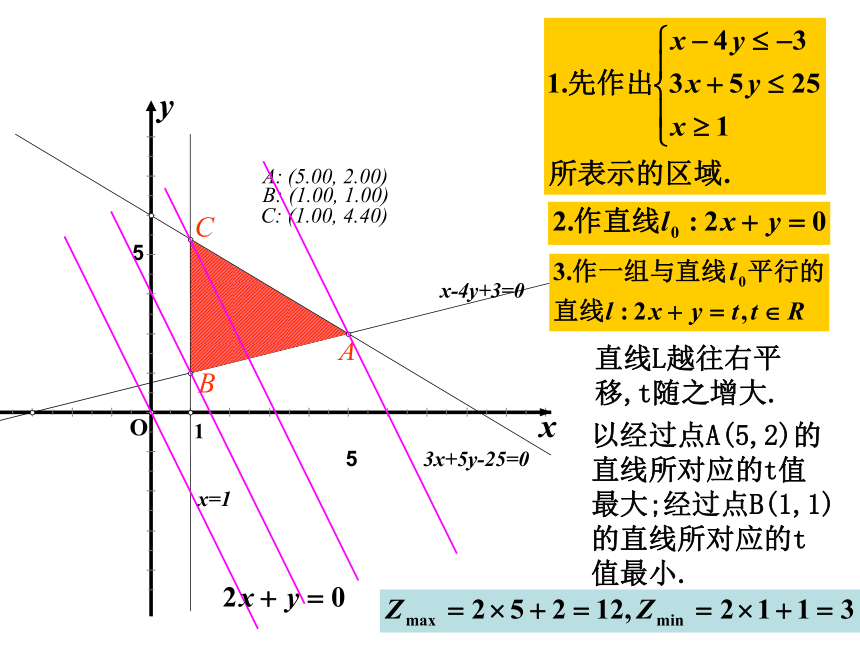
直线L越往右平移,t随之增大.
以经过点A(5,2)的直线所对应的t值最大;经过点B(1,1)的直线所对应的t值最小.
设z=2x+y,求满足
时,求z的最大值和最小值.
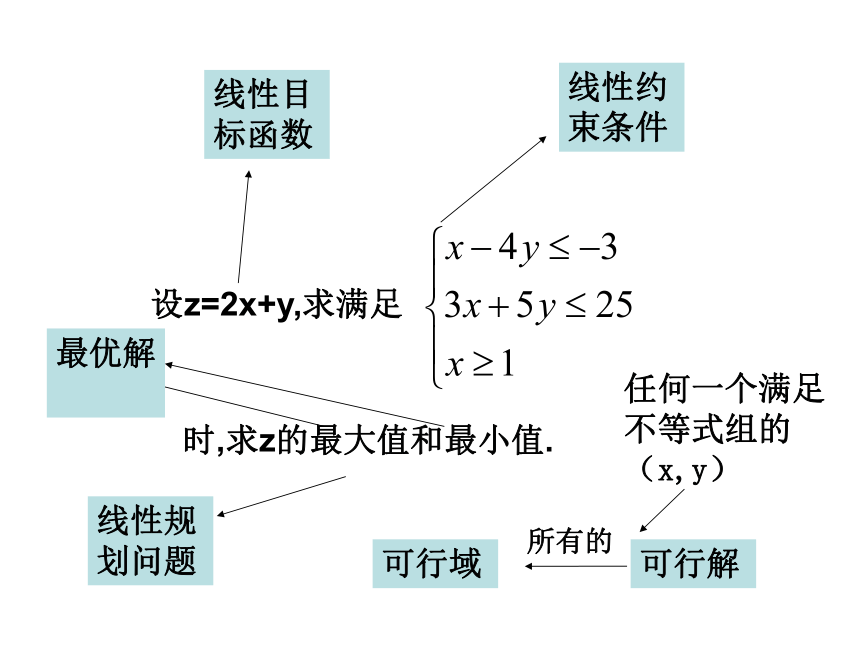
线性目标函数
线性约束条件
线性规划问题
任何一个满足不等式组的(x,y)
可行解
可行域
所有的
最优解
有关概念
由x,y 的不等式(或方程)组成的不等式组称为x,y 的约束条件。关于x,y 的一次不等式或方程组成的不等式组称为x,y 的线性约束条件。欲达到最大值或最小值所涉及的变量x,y 的解析式称为目标函数。关于x,y 的一次目标函数称为线性目标函数。求线性目标函数在线性约束条件下的最大值或最小值问题称为线性规划问题。满足线性约束条件的解(x,y)称为可行解。所有可行解组成的集合称为可行域。使目标函数取得最大值或最小值的可行解称为最优解。
5
5
x=1
x-4y+3=0
3x+5y-25=0
1
A
B
C
C:
(1.00, 4.40)
A:
(5.00, 2.00)
B:
(1.00, 1.00)
O
x
y
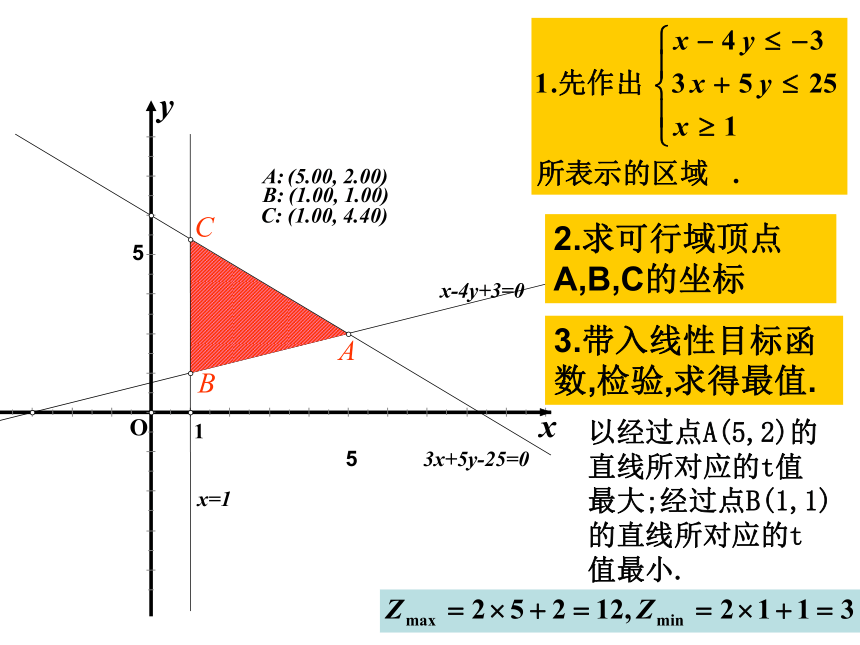
以经过点A(5,2)的直线所对应的t值最大;经过点B(1,1)的直线所对应的t值最小.
2.求可行域顶点A,B,C的坐标
3.带入线性目标函数,检验,求得最值.
解线性规划问题的一般步骤:
第一步:在平面直角坐标系中作出可行域;
第二步:联立方程组,求出可行域顶点对应的坐标;
第三步:带入目标函数检验,从而求出目标函数的最大值或最小值。
线性规划解题步骤
(1)已知
求z=2x+y的最大值和最小值。
5
5
1
O
x
y
x-y=0
x+y-1=0
1
-1
y+1=0
A(2,-1)
B(-1,-1)
C(1/2,1/2)
练习1、已知
求z=3x+5y的最大值和最小值。
5
5
1
O
x
y
1
-1
5x+3y=15
X-5y=3
y=x+1
A(-2,-1)
B(3/2,5/2)
C(3,0)
解线性规划问题的一般步骤:
第一步:在平面直角坐标系中作出可行域;
第二步:联立方程组,求出可行域顶点对应的坐标;
第三步:带入目标函数检验,从而求出目标函数的最大值或最小值。
线性规划解题步骤
实际应用题
例2.某工厂生产甲、乙两种产品,生产1t甲种产品需要A种原料4t、 B种原料12t,产生的利润为2万元;生产1t乙种产品需要A种原料1t、 B种原料9t,产生的利润为1万元。现有库存A种原料10t、 B种原料60t,如何安排生产才能使利润最大?
A种原料 B种原料 利润
甲种产品 4 12 2
乙种产品 1 9 1
现有库存 10 60
有关数据列表如下:
设生产甲、乙两种产品的吨数
分别为x、y
利润
何时达到最大?
解线性规划应用问题的一般步骤:
2)设好变元并列出不等式组和目标函数
4)在可行域内求目标函数的最优解
1)理清题意,列出表格:
5)还原成实际问题
(准确作图,准确计算)
3)由二元一次不等式表示的平面区域作出可行域;
一.复习回顾
1.在同一坐标系上作出下列直线:
2x+y=0;2x+y=1;2x+y=-3;2x+y=4;2x+y=7
x
Y
o
2.作出下列不等式组所表示的平面区域
5
5
x=1
x-4y+3=0
3x+5y-25=0
1
A
B
C
C:
(1.00, 4.40)
A:
(5.00, 2.00)
B:
(1.00, 1.00)
O
x
y
问题1:x 有无最大(小)值?
问题2:y 有无最大(小)值?
问题3:2x+y 有无最大(小)值?
二.提出问题
把上面两个问题综合起来:
设z=2x+y,求满足
时,求z的最大值和最小值.
5
5
x=1
x-4y+3=0
3x+5y-25=0
1
A
B
C
C:
(1.00, 4.40)
A:
(5.00, 2.00)
B:
(1.00, 1.00)
O
x
y
直线L越往右平移,t随之增大.
以经过点A(5,2)的直线所对应的t值最大;经过点B(1,1)的直线所对应的t值最小.
设z=2x+y,求满足
时,求z的最大值和最小值.
线性目标函数
线性约束条件
线性规划问题
任何一个满足不等式组的(x,y)
可行解
可行域
所有的
最优解
有关概念
由x,y 的不等式(或方程)组成的不等式组称为x,y 的约束条件。关于x,y 的一次不等式或方程组成的不等式组称为x,y 的线性约束条件。欲达到最大值或最小值所涉及的变量x,y 的解析式称为目标函数。关于x,y 的一次目标函数称为线性目标函数。求线性目标函数在线性约束条件下的最大值或最小值问题称为线性规划问题。满足线性约束条件的解(x,y)称为可行解。所有可行解组成的集合称为可行域。使目标函数取得最大值或最小值的可行解称为最优解。
5
5
x=1
x-4y+3=0
3x+5y-25=0
1
A
B
C
C:
(1.00, 4.40)
A:
(5.00, 2.00)
B:
(1.00, 1.00)
O
x
y
以经过点A(5,2)的直线所对应的t值最大;经过点B(1,1)的直线所对应的t值最小.
2.求可行域顶点A,B,C的坐标
3.带入线性目标函数,检验,求得最值.
解线性规划问题的一般步骤:
第一步:在平面直角坐标系中作出可行域;
第二步:联立方程组,求出可行域顶点对应的坐标;
第三步:带入目标函数检验,从而求出目标函数的最大值或最小值。
线性规划解题步骤
(1)已知
求z=2x+y的最大值和最小值。
5
5
1
O
x
y
x-y=0
x+y-1=0
1
-1
y+1=0
A(2,-1)
B(-1,-1)
C(1/2,1/2)
练习1、已知
求z=3x+5y的最大值和最小值。
5
5
1
O
x
y
1
-1
5x+3y=15
X-5y=3
y=x+1
A(-2,-1)
B(3/2,5/2)
C(3,0)
解线性规划问题的一般步骤:
第一步:在平面直角坐标系中作出可行域;
第二步:联立方程组,求出可行域顶点对应的坐标;
第三步:带入目标函数检验,从而求出目标函数的最大值或最小值。
线性规划解题步骤
实际应用题
例2.某工厂生产甲、乙两种产品,生产1t甲种产品需要A种原料4t、 B种原料12t,产生的利润为2万元;生产1t乙种产品需要A种原料1t、 B种原料9t,产生的利润为1万元。现有库存A种原料10t、 B种原料60t,如何安排生产才能使利润最大?
A种原料 B种原料 利润
甲种产品 4 12 2
乙种产品 1 9 1
现有库存 10 60
有关数据列表如下:
设生产甲、乙两种产品的吨数
分别为x、y
利润
何时达到最大?
解线性规划应用问题的一般步骤:
2)设好变元并列出不等式组和目标函数
4)在可行域内求目标函数的最优解
1)理清题意,列出表格:
5)还原成实际问题
(准确作图,准确计算)
3)由二元一次不等式表示的平面区域作出可行域;
