2020-2021学年度人教版小学六年级数学上册第八单元检测试题(含答案)
文档属性
| 名称 | 2020-2021学年度人教版小学六年级数学上册第八单元检测试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 635.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-28 15:43:59 | ||
图片预览



文档简介
绝密★启用前
2020-2021学年度人教版小学六年级数学上册第八单元检测试题(含答案)
一、填空题
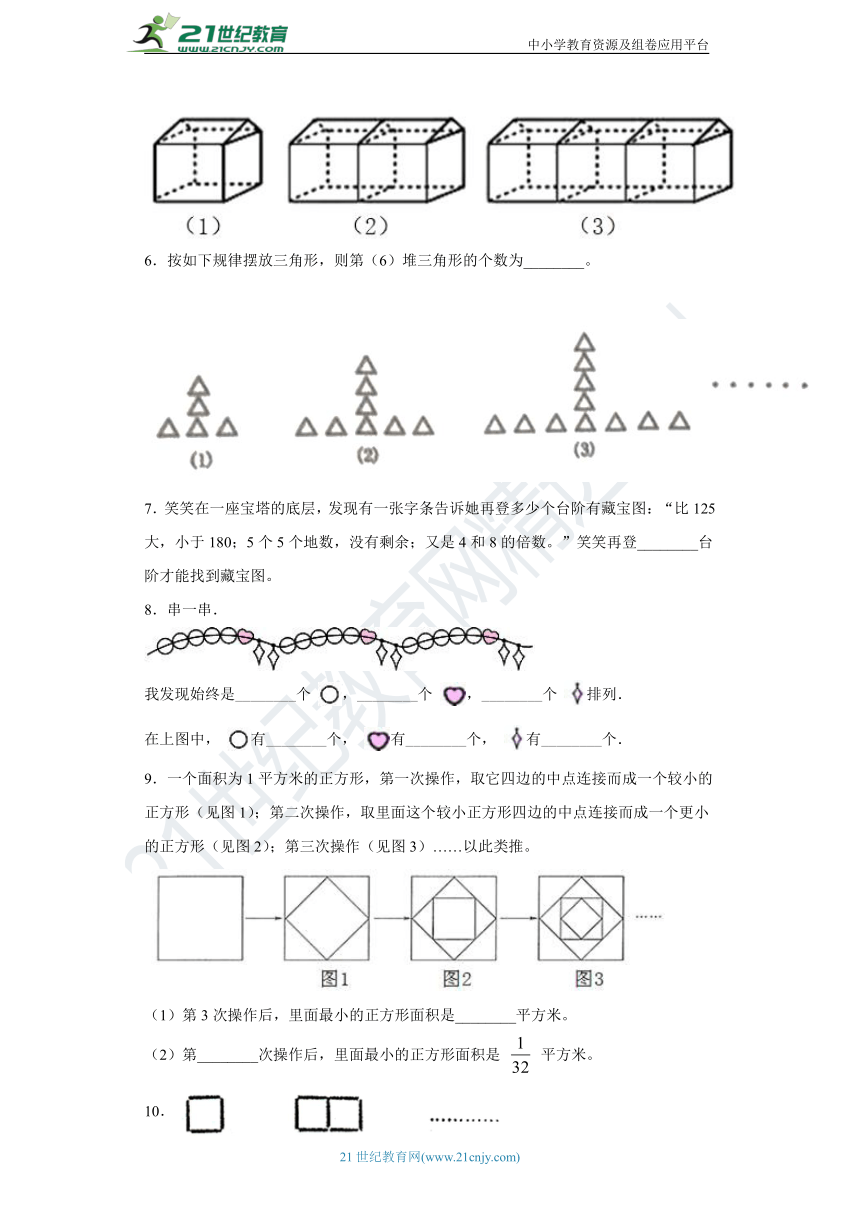
1.观察并填空。
1.
图形
……
正方形的个数
(______)
(______)
(______)
……
2. 第4个“F”图形需用________个正方形拼成。
3. 第n个“F”图形需用________个正方形拼成。
2.如图是打国际长途电话所需付的电话费与通话时间之间的关系图。
(1)打2分钟需要_____元电话费,3分钟以上每分钟_____元。
(2)打6分钟需要_____元,10.4元打了_____分钟。
3.找规律.
________ ________
4.小明按照如图的方法用灰色和白色正方形摆图形.
当中间摆n个灰色的正方形时,四周共需要摆________个白色正方形.
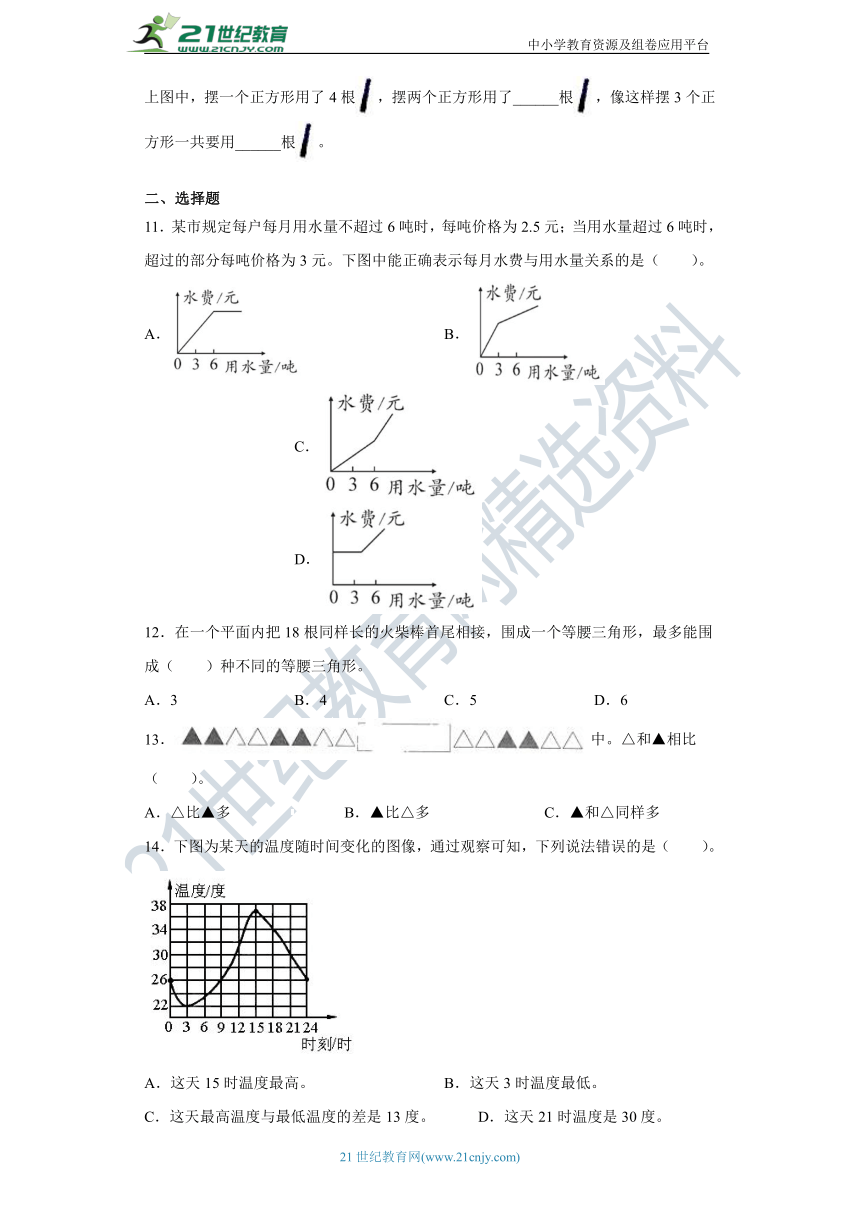
5.搭建如图(1)的单顶帐篷需要17根钢管,若这样的帐篷按图(2)、图(3)的方式串起来搭建,则可节省结合处的钢管,那么串搭20顶这样的帐篷需要________根钢管。
6.按如下规律摆放三角形,则第(6)堆三角形的个数为________。
7.笑笑在一座宝塔的底层,发现有一张字条告诉她再登多少个台阶有藏宝图:“比125大,小于180;5个5个地数,没有剩余;又是4和8的倍数。”笑笑再登________台阶才能找到藏宝图。
8.串一串.
我发现始终是________个 ,________个 ,________个 排列.
在上图中, 有________个, 有________个, 有________个.
9.一个面积为1平方米的正方形,第一次操作,取它四边的中点连接而成一个较小的正方形(见图1);第二次操作,取里面这个较小正方形四边的中点连接而成一个更小的正方形(见图2);第三次操作(见图3)……以此类推。
(1)第3次操作后,里面最小的正方形面积是________平方米。
(2)第________次操作后,里面最小的正方形面积是 false 平方米。
10.
上图中,摆一个正方形用了4根,摆两个正方形用了______根,像这样摆3个正方形一共要用______根。
二、选择题
11.某市规定每户每月用水量不超过6吨时,每吨价格为2.5元;当用水量超过6吨时,超过的部分每吨价格为3元。下图中能正确表示每月水费与用水量关系的是( )。
A. B. C.? D.
12.在一个平面内把18根同样长的火柴棒首尾相接,围成一个等腰三角形,最多能围成( )种不同的等腰三角形。
A.3 B.4 C.5 D.6
13.中。△和▲相比( )。
A.△比▲多???? B.▲比△多? C.▲和△同样多
14.下图为某天的温度随时间变化的图像,通过观察可知,下列说法错误的是( )。
A.这天15时温度最高。 B.这天3时温度最低。
C.这天最高温度与最低温度的差是13度。?? D.这天21时温度是30度。
15.按照“ ”的规律画图形,第830个图形是(?? ).
A. B. C. D.
三、判断题
16.按1、8、27、( )、125、216的规律排,括号中的数应为64. (_____)
17.8个点可以连成20条线段。(________)
18.如图,第五个点阵中点的个数是17个.(____)
19.用小棒照图搭正方形,搭一个正方形用4根,搭两个正方形用7根,搭a个正方形有4a根._____
20.根据几个乘法算式找出的得数的规律,适用于所有具有同一特征算式的结果._____
四、计算题
21.直接写得数。
2-142.5%= 0.85×100%= false÷false= 4.9×false= 0×false=
40%×false= false×false= false-10%= false×false= false÷60%=
22.看图列式计算。
23.看图列式计算。
24.解方程。
60%x+25=40 24-120%x=18
35%x-25%x=1 (1-25%)x=45
25.计算下面各题.
(1)false (2)false (3)false
五、解答题
26.一个杯子口朝上,翻动一次杯口朝下,翻动两次杯口朝上,那么翻动56次杯口朝哪里?并说明理由.
27.欣社区公园要铺设一条人行道,人行道长80米,宽1.6米.现在用边长都是0.4米的红、黄两种正方形地砖铺设(如图是铺设的局部图示).
①请帮忙算算铺设这条人行一共需多少块地砖?(不计损耗)
下题不计入总分,有时间可以试试.
②铺设这条人行道一共需要多少块红色地砖?(不计损耗)
28.下图是2017年某大型超市夏季饮料销售净利润统计图。
(1)矿泉水利润占全部的百分之几?
(2)若矿泉水的利润是110万元,那么总利润是多少万元?
29.下图是一个果园的统计图,请你算出一共有多少棵果树?其中桃树有多少棵?苹果树有多少棵?
30.图中是林场育苗基地树苗情况统计图。
(1)已知柳树有3500棵,这些树苗的总数是多少棵?
(2)松树比柏树多百分之几?
参考答案
1.6 10 14 18 4n+2
【解析】
【分析】
(1)根据已知图形数出正方形个数即可;(2)题,根据第一题可得:相邻两个图形中正方形个数依次增加4个,第4个图形中正方形个数通过第3个图形中正方形个数加4即可解答;(3)第n个图形中正方形个数为6+(n-1)×4,由此即可解答。
【详解】
1.6;10;14.
2.第四个图形中正方形个数为:14+4=18(个);
3.第n个图形中正方形个数是(4n+2)个。
2.2.4 1 5.4 11
【解析】
【分析】
(1)根据折线统计图可知:国际长途电话前3分钟的花费为2.4元,所以打2分钟为2.4元,3分钟以上每分钟:(4.4-2.4)÷(5-3)=1(元)
(2)根据(1)的计算结果,计算打6分钟付费情况:(6-3)×1+2.4=5.4(元);10.4元可以打:(10.4-2.4)÷1+3=11(分钟)。
【详解】
(1)根据折线统计图可知:国际长途电话前3分钟的花费为2.4元,
所以打2分钟为2.4元。
3分钟以上每分钟:
(4.4﹣2.4)÷(5﹣3)
=2÷2
=1(元)
答:打2分钟需要2.4元电话费,3分钟以上每分钟1元。
(2)(6﹣3)×1+2.4
=3+2.4
=5.4(元)
(10.4-2.4)÷1+3
=8+3
=11(分钟)
答:打6分钟需要5.4元,10.4元打了11分钟。
故答案为2.4;1;5.4;11。
【点睛】
本题考查折线统计图的分析,关键要从图中找到国际长途电话所需付的电话费与通话时间之间的关系。
3.
【解析】
【分析】
【详解】
略
4.2n+6
【解析】
【分析】
观察图形可得排列规律:中间一行只有2个白色正方形,剩下两行的白色正方形的个数都等于灰色正方形的个数加2,据此解答即可.
【详解】
当中间摆n个灰色的正方形时,四周共需要摆白色正方形: 2+(n+2)×2=2n+6(个)
答:当中间摆n个灰色的正方形时,四周共需要摆 2n+6个白色正方形.
故答案为02n+6.
5.226
【解析】
【分析】
观察图可得规律:串搭n顶这样的帐篷需要11n+6根钢管,据此列式解答。
【详解】
20×11+6
=220+6
=226(根)
【点睛】
此题主要考查了数形结合的知识,数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
6.20个
【解析】
【分析】
规律:三角形个数=图形个数×3+2,按照这样的规律计算即可。
【详解】
6×3+2=20(个)
【点睛】
本题考查数与形,解答本题的关键是找到图形变化的规律三角形个数=图形个数×3+2。
7.160个
【解析】
【分析】
因为台阶数是4、5、8的倍数,所以从4、5、8的最小公倍数中判断台阶数即可。
【详解】
4×8=32,32×5=160,160既是4和8的倍数,又是5的倍数,125<160<180,所以台阶数是160个。
【点睛】
此题从4、5、8的最小公倍数入手,找出适合的倍数。
8.5;1;2;15;3;6
【解析】
【分析】
解答本题的关键是找出图形的排列规律,然后再结合乘法的意义,即求几个相同加数的和,用乘法计算,进行解答即可.
【详解】
观察图形可知,该图形可分为3组,每组有5个、1个、2个组成,所以该图形始终有5个、1个、2个排列;
5×3=15(个),1×3=3(个),2×3=6(个),所以图中个有15个、有3个、有6个.
故答案为5;1;2;15;3;6.
9.false 5
【解析】
【分析】
从图中观察,每次取的都是正方形每条边长的一半,而且里面的正方形是所取正方形面积的false, 所以进行几次操作,里面最小的正方形面积就是(几个false相乘)平方米。
【详解】
(1)第3次操作后,里面最小的正方形面积是false×false×false=false平方米;
(2)第5次操作后,里面最小的正方形面积是false平方米。
10.7 10
【解析】
【分析】
【详解】
从图中可以得出,摆几个长方形,就是把3加几次再加上1
11.C
【解析】
【分析】
水费的增加随用水量的增加而增加,当用水量超过6吨时,超过的部分每吨价格比6吨内明显上升,所以折线也明显上升,据此判断。
【详解】
某市规定每户每月用水量不超过6吨时,每吨价格为2.5元;当用水量超过6吨时,超过的部分每吨价格为3元。下图中能正确表示每月水费与用水量关系的是:
。
故答案为:C。
【点睛】
此题主要考查了用图像表示变化关系。
12.B
【解析】
【分析】
根据三角形两边之和大于第三边,以及等腰三角形的特征,将18分解成三个数相加的和,再看哪三个数满足构成三角形的条件即可。
【详解】
有5+5+8,6+6+6,7+7+4,8+8+2一共四种。
故答案为:B。
【点睛】
本题考查等腰三角形的特征和三角形三边的关系,需要注意等边三角形也属于等腰三角形,不要漏了情况。
13.C
【解析】
【分析】
观察外面图形的特征,图形是两个两个为一组,根据图形的规律确定两种图形的个数即可。
【详解】
图形按2个▲,2个△排列,最前面是2个▲,最后面是2个△。所以△和▲同样多。
故答案为:C。
【点睛】
解这类题时,先找到图形的排列规律,后根据规律解题即可。
14.C
【解析】
【分析】
图中横轴表示时刻,竖轴表示温度,根据相应的时间对应的温度判断各个选项的说法即可。
【详解】
A、最高温度是37度是15时,此选项正确;
B、温度最低是22度是3时,此选项正确;
C、最高温度和最低温度差是37-22=15(度),此选项错误;
D、21时对应的温度是30度,此选项正确。
故答案为:C。
【点睛】
理解折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。
15.C
【解析】
【分析】
每8个图形一组,用830除以8求出商和余数,余数是几,最后一个图形就与每组中的第几个图形相同.
【详解】
830÷8=103……6,第830个图形是圆.
故答案为C.
16.正确
【解析】
【分析】
【详解】
略
17.×
【解析】
【分析】
3个点连成线段的条数:?1+2=3(条),4个点连成线段的条数:1+2+3=6(条),5个点连成线段的条数:?1+2+3+4=10(条),由此得出规律:n个点的线段数是:?1+2+3+4+……+?n-1条线段,据此规律解答即可。
【详解】
8个点可以连成线段数为1+2+3+4+5+6+7=28(条),所以本题说法错误。
故答案为:×。
【点睛】
本题考查探索规律,解答本题的关键是根据数形结合的思想,在草稿纸上画出几个点,然后得出规律,根据规律解答问题。
18.√
【解析】
【详解】
第一个点阵中点的个数:1个
第二个点阵中点的个数:1+4=5(个)
第三个点阵中点的个数:1+4+4=9(个)
……
第n个点阵中点的个数:1+4(n﹣1)=(4n-3)(个)
……
第五个点阵中点的个数:
4×5-3
=20-3
=17(个)
答:第五个点阵中点的个数是23个.所以原说法正确.
故答案为:√.
19.×
【解析】
【详解】
观察第一个图得,搭一个正方形要火柴4根;
观察第二个图得,搭两个正方形要火柴(4+3)根,即7根;
观察第三个图得,搭三个正方形要火柴(4+3×2)根,即10根,
所以搭a个正方形要火柴4+3×(a﹣1)=3a+1根.
故答案为:×.
20.√
【解析】
【分析】
【详解】
如
1×9=9
12×9=108
123×9=1107
…
根据几个乘法算式找出的得数的规律,适用于所有具有同一特征算式的结果,这种说法正确.
故答案为:√.
21.0.575;0.85;false;1.4;0;
1;false;0.3;1;1
【解析】
【分析】
【详解】
略
22.150个
【解析】
【分析】
篮球比足球多足球的20%,所以篮球是足球的(1+20%),用125×(1+20%)即可求解。
【详解】
125×(1+20%)
=125×1.2
=150(个)
23.76元
【解析】
【分析】
降低原价的20%,那么现价就是原价的(1-20%),用95×(1-20%)即可求解。
【详解】
95×(1-20%)
=95×0.8
=76(元)
24.25;5;10;60
【解析】
【分析】
利用等式的解方程即可。
【详解】
60%x+25=40
解:0.6x=40-25
0.6x=15
x=25
24-120%x=18
解:24-1.2x=18
24-18=1.2x
1.2x=6
x=5
35%x-25%x=1
解:0.35x-0.25x=1
0.1x=1
x=10
(1-25%)x=45
解:0.75x=45
x=60
25.(1)false;(2)false;(3)false
【解析】
【分析】
【详解】
(1)false
=false
=false
=false
(2)false
=false
=false
=false
(3)false
=false
=false
=false
=false
=false
26.朝上,翻动偶数次与原来状态相同,翻动奇数次与原来状态相反
【解析】
【分析】
【详解】
由题意可知:杯子翻动杯子1次,杯口朝下,翻动2次杯口朝上,翻动3次,杯口朝下,翻动4次,杯口朝上…,得出:翻动偶数次与原来状态相同,翻动奇数次与原来状态相反;
因为56是偶数;
所以翻动56次,杯口朝上.
答:翻动56次,杯口朝上.
27.800块,200块
【解析】
试题分析:①先求出宽边需要的块数,再求出长边需要的块数,相乘即可求解;
②观察天象可知从左往右每16块地砖中有4块红色地砖,依此列式即可求解.
解:①1.6÷0.4=4(块),
80÷0.4=200(块),
200×4=800(块).
答:铺设这条人行一共需800块地砖;
②800÷16×4
=50×4
=200(块).
答:铺设这条人行道一共需要200块红色地砖.
点评:考查了数与形结合的规律,本题得到铺设一条人行道宽边需要的块数和长边需要的块数是解题的关键.
28.(1)22%;(2)500万元
【解析】
【分析】
(1)用“1―(23%+5%+35%+15%)”即可求出矿泉水利润占全部的百分之几。
(2)根据“总利润×矿泉水利润占全部的百分之几=矿泉水的利润”这一关系式,求出总利润即可。
【详解】
(1)1―(23%+5%+35%+15%)
=1―78%
=22%
答:矿泉水利润占全部的22%。
(2)110÷22%=500(万元)
答:总利润是500万元。
【点睛】
本题综合性较强,熟练掌握基础知识是关键。
29.3000棵;900棵;1650棵
【解析】
【分析】
根据扇形统计图可知,把果园果树总量看作单位“1”,用1减去苹果树的百分率,再减去桃树的百分率就是梨树的百分率,用梨树的具体数量除以对应的百分率即可求出单位“1”具体的数量,再用果树总量分别乘以苹果数和桃树的百分率即可。
【详解】
450÷(1-55%-30%)
=450÷15%
=3000(棵)
3000×30%=900(棵)
3000×55%=1650(棵)
答:一共有3000棵果树,桃树900棵,苹果树1650棵。
【点睛】
从问题出发,能够从扇形统计图中获得相关信息是解题的基础,已知一个数的百分之几是多少,求这个数时,用除法计算;求一个数的百分之几是多少时,用乘法计算。
30.(1)14000棵;(2)50%
【解析】
【分析】
(1)根据“总棵数×25%=柳树棵数”,求出总棵数即可。
(2)先计算出松树和柏树各有多少棵,再根据“(松树树苗棵数-柏树树苗棵数)÷柏树树苗棵数=松树比柏树多百分之几”求解即可。
【详解】
(1)3500÷25%=14000(棵)
答:这些树苗的总数是14000棵。
(2)松树棵数:14000×15%=2100(棵);
柏树棵数:14000×10%=1400(棵)
(2100-1400)÷1400
=700÷1400
=50%
答:松树比柏树多50%。
【点睛】
本题综合性较强,能够灵活运用基础知识解答是关键。
2020-2021学年度人教版小学六年级数学上册第八单元检测试题(含答案)
一、填空题
1.观察并填空。
1.
图形
……
正方形的个数
(______)
(______)
(______)
……
2. 第4个“F”图形需用________个正方形拼成。
3. 第n个“F”图形需用________个正方形拼成。
2.如图是打国际长途电话所需付的电话费与通话时间之间的关系图。
(1)打2分钟需要_____元电话费,3分钟以上每分钟_____元。
(2)打6分钟需要_____元,10.4元打了_____分钟。
3.找规律.
________ ________
4.小明按照如图的方法用灰色和白色正方形摆图形.
当中间摆n个灰色的正方形时,四周共需要摆________个白色正方形.
5.搭建如图(1)的单顶帐篷需要17根钢管,若这样的帐篷按图(2)、图(3)的方式串起来搭建,则可节省结合处的钢管,那么串搭20顶这样的帐篷需要________根钢管。
6.按如下规律摆放三角形,则第(6)堆三角形的个数为________。
7.笑笑在一座宝塔的底层,发现有一张字条告诉她再登多少个台阶有藏宝图:“比125大,小于180;5个5个地数,没有剩余;又是4和8的倍数。”笑笑再登________台阶才能找到藏宝图。
8.串一串.
我发现始终是________个 ,________个 ,________个 排列.
在上图中, 有________个, 有________个, 有________个.
9.一个面积为1平方米的正方形,第一次操作,取它四边的中点连接而成一个较小的正方形(见图1);第二次操作,取里面这个较小正方形四边的中点连接而成一个更小的正方形(见图2);第三次操作(见图3)……以此类推。
(1)第3次操作后,里面最小的正方形面积是________平方米。
(2)第________次操作后,里面最小的正方形面积是 false 平方米。
10.
上图中,摆一个正方形用了4根,摆两个正方形用了______根,像这样摆3个正方形一共要用______根。
二、选择题
11.某市规定每户每月用水量不超过6吨时,每吨价格为2.5元;当用水量超过6吨时,超过的部分每吨价格为3元。下图中能正确表示每月水费与用水量关系的是( )。
A. B. C.? D.
12.在一个平面内把18根同样长的火柴棒首尾相接,围成一个等腰三角形,最多能围成( )种不同的等腰三角形。
A.3 B.4 C.5 D.6
13.中。△和▲相比( )。
A.△比▲多???? B.▲比△多? C.▲和△同样多
14.下图为某天的温度随时间变化的图像,通过观察可知,下列说法错误的是( )。
A.这天15时温度最高。 B.这天3时温度最低。
C.这天最高温度与最低温度的差是13度。?? D.这天21时温度是30度。
15.按照“ ”的规律画图形,第830个图形是(?? ).
A. B. C. D.
三、判断题
16.按1、8、27、( )、125、216的规律排,括号中的数应为64. (_____)
17.8个点可以连成20条线段。(________)
18.如图,第五个点阵中点的个数是17个.(____)
19.用小棒照图搭正方形,搭一个正方形用4根,搭两个正方形用7根,搭a个正方形有4a根._____
20.根据几个乘法算式找出的得数的规律,适用于所有具有同一特征算式的结果._____
四、计算题
21.直接写得数。
2-142.5%= 0.85×100%= false÷false= 4.9×false= 0×false=
40%×false= false×false= false-10%= false×false= false÷60%=
22.看图列式计算。
23.看图列式计算。
24.解方程。
60%x+25=40 24-120%x=18
35%x-25%x=1 (1-25%)x=45
25.计算下面各题.
(1)false (2)false (3)false
五、解答题
26.一个杯子口朝上,翻动一次杯口朝下,翻动两次杯口朝上,那么翻动56次杯口朝哪里?并说明理由.
27.欣社区公园要铺设一条人行道,人行道长80米,宽1.6米.现在用边长都是0.4米的红、黄两种正方形地砖铺设(如图是铺设的局部图示).
①请帮忙算算铺设这条人行一共需多少块地砖?(不计损耗)
下题不计入总分,有时间可以试试.
②铺设这条人行道一共需要多少块红色地砖?(不计损耗)
28.下图是2017年某大型超市夏季饮料销售净利润统计图。
(1)矿泉水利润占全部的百分之几?
(2)若矿泉水的利润是110万元,那么总利润是多少万元?
29.下图是一个果园的统计图,请你算出一共有多少棵果树?其中桃树有多少棵?苹果树有多少棵?
30.图中是林场育苗基地树苗情况统计图。
(1)已知柳树有3500棵,这些树苗的总数是多少棵?
(2)松树比柏树多百分之几?
参考答案
1.6 10 14 18 4n+2
【解析】
【分析】
(1)根据已知图形数出正方形个数即可;(2)题,根据第一题可得:相邻两个图形中正方形个数依次增加4个,第4个图形中正方形个数通过第3个图形中正方形个数加4即可解答;(3)第n个图形中正方形个数为6+(n-1)×4,由此即可解答。
【详解】
1.6;10;14.
2.第四个图形中正方形个数为:14+4=18(个);
3.第n个图形中正方形个数是(4n+2)个。
2.2.4 1 5.4 11
【解析】
【分析】
(1)根据折线统计图可知:国际长途电话前3分钟的花费为2.4元,所以打2分钟为2.4元,3分钟以上每分钟:(4.4-2.4)÷(5-3)=1(元)
(2)根据(1)的计算结果,计算打6分钟付费情况:(6-3)×1+2.4=5.4(元);10.4元可以打:(10.4-2.4)÷1+3=11(分钟)。
【详解】
(1)根据折线统计图可知:国际长途电话前3分钟的花费为2.4元,
所以打2分钟为2.4元。
3分钟以上每分钟:
(4.4﹣2.4)÷(5﹣3)
=2÷2
=1(元)
答:打2分钟需要2.4元电话费,3分钟以上每分钟1元。
(2)(6﹣3)×1+2.4
=3+2.4
=5.4(元)
(10.4-2.4)÷1+3
=8+3
=11(分钟)
答:打6分钟需要5.4元,10.4元打了11分钟。
故答案为2.4;1;5.4;11。
【点睛】
本题考查折线统计图的分析,关键要从图中找到国际长途电话所需付的电话费与通话时间之间的关系。
3.
【解析】
【分析】
【详解】
略
4.2n+6
【解析】
【分析】
观察图形可得排列规律:中间一行只有2个白色正方形,剩下两行的白色正方形的个数都等于灰色正方形的个数加2,据此解答即可.
【详解】
当中间摆n个灰色的正方形时,四周共需要摆白色正方形: 2+(n+2)×2=2n+6(个)
答:当中间摆n个灰色的正方形时,四周共需要摆 2n+6个白色正方形.
故答案为02n+6.
5.226
【解析】
【分析】
观察图可得规律:串搭n顶这样的帐篷需要11n+6根钢管,据此列式解答。
【详解】
20×11+6
=220+6
=226(根)
【点睛】
此题主要考查了数形结合的知识,数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
6.20个
【解析】
【分析】
规律:三角形个数=图形个数×3+2,按照这样的规律计算即可。
【详解】
6×3+2=20(个)
【点睛】
本题考查数与形,解答本题的关键是找到图形变化的规律三角形个数=图形个数×3+2。
7.160个
【解析】
【分析】
因为台阶数是4、5、8的倍数,所以从4、5、8的最小公倍数中判断台阶数即可。
【详解】
4×8=32,32×5=160,160既是4和8的倍数,又是5的倍数,125<160<180,所以台阶数是160个。
【点睛】
此题从4、5、8的最小公倍数入手,找出适合的倍数。
8.5;1;2;15;3;6
【解析】
【分析】
解答本题的关键是找出图形的排列规律,然后再结合乘法的意义,即求几个相同加数的和,用乘法计算,进行解答即可.
【详解】
观察图形可知,该图形可分为3组,每组有5个、1个、2个组成,所以该图形始终有5个、1个、2个排列;
5×3=15(个),1×3=3(个),2×3=6(个),所以图中个有15个、有3个、有6个.
故答案为5;1;2;15;3;6.
9.false 5
【解析】
【分析】
从图中观察,每次取的都是正方形每条边长的一半,而且里面的正方形是所取正方形面积的false, 所以进行几次操作,里面最小的正方形面积就是(几个false相乘)平方米。
【详解】
(1)第3次操作后,里面最小的正方形面积是false×false×false=false平方米;
(2)第5次操作后,里面最小的正方形面积是false平方米。
10.7 10
【解析】
【分析】
【详解】
从图中可以得出,摆几个长方形,就是把3加几次再加上1
11.C
【解析】
【分析】
水费的增加随用水量的增加而增加,当用水量超过6吨时,超过的部分每吨价格比6吨内明显上升,所以折线也明显上升,据此判断。
【详解】
某市规定每户每月用水量不超过6吨时,每吨价格为2.5元;当用水量超过6吨时,超过的部分每吨价格为3元。下图中能正确表示每月水费与用水量关系的是:
。
故答案为:C。
【点睛】
此题主要考查了用图像表示变化关系。
12.B
【解析】
【分析】
根据三角形两边之和大于第三边,以及等腰三角形的特征,将18分解成三个数相加的和,再看哪三个数满足构成三角形的条件即可。
【详解】
有5+5+8,6+6+6,7+7+4,8+8+2一共四种。
故答案为:B。
【点睛】
本题考查等腰三角形的特征和三角形三边的关系,需要注意等边三角形也属于等腰三角形,不要漏了情况。
13.C
【解析】
【分析】
观察外面图形的特征,图形是两个两个为一组,根据图形的规律确定两种图形的个数即可。
【详解】
图形按2个▲,2个△排列,最前面是2个▲,最后面是2个△。所以△和▲同样多。
故答案为:C。
【点睛】
解这类题时,先找到图形的排列规律,后根据规律解题即可。
14.C
【解析】
【分析】
图中横轴表示时刻,竖轴表示温度,根据相应的时间对应的温度判断各个选项的说法即可。
【详解】
A、最高温度是37度是15时,此选项正确;
B、温度最低是22度是3时,此选项正确;
C、最高温度和最低温度差是37-22=15(度),此选项错误;
D、21时对应的温度是30度,此选项正确。
故答案为:C。
【点睛】
理解折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。
15.C
【解析】
【分析】
每8个图形一组,用830除以8求出商和余数,余数是几,最后一个图形就与每组中的第几个图形相同.
【详解】
830÷8=103……6,第830个图形是圆.
故答案为C.
16.正确
【解析】
【分析】
【详解】
略
17.×
【解析】
【分析】
3个点连成线段的条数:?1+2=3(条),4个点连成线段的条数:1+2+3=6(条),5个点连成线段的条数:?1+2+3+4=10(条),由此得出规律:n个点的线段数是:?1+2+3+4+……+?n-1条线段,据此规律解答即可。
【详解】
8个点可以连成线段数为1+2+3+4+5+6+7=28(条),所以本题说法错误。
故答案为:×。
【点睛】
本题考查探索规律,解答本题的关键是根据数形结合的思想,在草稿纸上画出几个点,然后得出规律,根据规律解答问题。
18.√
【解析】
【详解】
第一个点阵中点的个数:1个
第二个点阵中点的个数:1+4=5(个)
第三个点阵中点的个数:1+4+4=9(个)
……
第n个点阵中点的个数:1+4(n﹣1)=(4n-3)(个)
……
第五个点阵中点的个数:
4×5-3
=20-3
=17(个)
答:第五个点阵中点的个数是23个.所以原说法正确.
故答案为:√.
19.×
【解析】
【详解】
观察第一个图得,搭一个正方形要火柴4根;
观察第二个图得,搭两个正方形要火柴(4+3)根,即7根;
观察第三个图得,搭三个正方形要火柴(4+3×2)根,即10根,
所以搭a个正方形要火柴4+3×(a﹣1)=3a+1根.
故答案为:×.
20.√
【解析】
【分析】
【详解】
如
1×9=9
12×9=108
123×9=1107
…
根据几个乘法算式找出的得数的规律,适用于所有具有同一特征算式的结果,这种说法正确.
故答案为:√.
21.0.575;0.85;false;1.4;0;
1;false;0.3;1;1
【解析】
【分析】
【详解】
略
22.150个
【解析】
【分析】
篮球比足球多足球的20%,所以篮球是足球的(1+20%),用125×(1+20%)即可求解。
【详解】
125×(1+20%)
=125×1.2
=150(个)
23.76元
【解析】
【分析】
降低原价的20%,那么现价就是原价的(1-20%),用95×(1-20%)即可求解。
【详解】
95×(1-20%)
=95×0.8
=76(元)
24.25;5;10;60
【解析】
【分析】
利用等式的解方程即可。
【详解】
60%x+25=40
解:0.6x=40-25
0.6x=15
x=25
24-120%x=18
解:24-1.2x=18
24-18=1.2x
1.2x=6
x=5
35%x-25%x=1
解:0.35x-0.25x=1
0.1x=1
x=10
(1-25%)x=45
解:0.75x=45
x=60
25.(1)false;(2)false;(3)false
【解析】
【分析】
【详解】
(1)false
=false
=false
=false
(2)false
=false
=false
=false
(3)false
=false
=false
=false
=false
=false
26.朝上,翻动偶数次与原来状态相同,翻动奇数次与原来状态相反
【解析】
【分析】
【详解】
由题意可知:杯子翻动杯子1次,杯口朝下,翻动2次杯口朝上,翻动3次,杯口朝下,翻动4次,杯口朝上…,得出:翻动偶数次与原来状态相同,翻动奇数次与原来状态相反;
因为56是偶数;
所以翻动56次,杯口朝上.
答:翻动56次,杯口朝上.
27.800块,200块
【解析】
试题分析:①先求出宽边需要的块数,再求出长边需要的块数,相乘即可求解;
②观察天象可知从左往右每16块地砖中有4块红色地砖,依此列式即可求解.
解:①1.6÷0.4=4(块),
80÷0.4=200(块),
200×4=800(块).
答:铺设这条人行一共需800块地砖;
②800÷16×4
=50×4
=200(块).
答:铺设这条人行道一共需要200块红色地砖.
点评:考查了数与形结合的规律,本题得到铺设一条人行道宽边需要的块数和长边需要的块数是解题的关键.
28.(1)22%;(2)500万元
【解析】
【分析】
(1)用“1―(23%+5%+35%+15%)”即可求出矿泉水利润占全部的百分之几。
(2)根据“总利润×矿泉水利润占全部的百分之几=矿泉水的利润”这一关系式,求出总利润即可。
【详解】
(1)1―(23%+5%+35%+15%)
=1―78%
=22%
答:矿泉水利润占全部的22%。
(2)110÷22%=500(万元)
答:总利润是500万元。
【点睛】
本题综合性较强,熟练掌握基础知识是关键。
29.3000棵;900棵;1650棵
【解析】
【分析】
根据扇形统计图可知,把果园果树总量看作单位“1”,用1减去苹果树的百分率,再减去桃树的百分率就是梨树的百分率,用梨树的具体数量除以对应的百分率即可求出单位“1”具体的数量,再用果树总量分别乘以苹果数和桃树的百分率即可。
【详解】
450÷(1-55%-30%)
=450÷15%
=3000(棵)
3000×30%=900(棵)
3000×55%=1650(棵)
答:一共有3000棵果树,桃树900棵,苹果树1650棵。
【点睛】
从问题出发,能够从扇形统计图中获得相关信息是解题的基础,已知一个数的百分之几是多少,求这个数时,用除法计算;求一个数的百分之几是多少时,用乘法计算。
30.(1)14000棵;(2)50%
【解析】
【分析】
(1)根据“总棵数×25%=柳树棵数”,求出总棵数即可。
(2)先计算出松树和柏树各有多少棵,再根据“(松树树苗棵数-柏树树苗棵数)÷柏树树苗棵数=松树比柏树多百分之几”求解即可。
【详解】
(1)3500÷25%=14000(棵)
答:这些树苗的总数是14000棵。
(2)松树棵数:14000×15%=2100(棵);
柏树棵数:14000×10%=1400(棵)
(2100-1400)÷1400
=700÷1400
=50%
答:松树比柏树多50%。
【点睛】
本题综合性较强,能够灵活运用基础知识解答是关键。
