人教版九年级上册22.1.4二次函数的图象和性质(Word版 含解析)
文档属性
| 名称 | 人教版九年级上册22.1.4二次函数的图象和性质(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 303.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 00:00:00 | ||
图片预览

文档简介
人教版九年级上册第二十二章二次函数22.1.4二次函数的图象和性质
一.解答题(共10小题)
1.某工厂大门是抛物线形水泥建筑,大门地面宽AB为4m,顶部C距离地面的高度为4.4m,现有一辆货车,其装货宽度为2.4m,高度2.8米,请通过计算说明该货车能否通过此大门?
2.如图,已知抛物线y=x2﹣(k+1)x+1的顶点A在x轴的负半轴上,且与一次函数y=﹣x+1交于点B和点C.
(1)求k的值;
(2)求△ABC的面积.
3.如图,已知二次函数y=x2+ax+3的图象经过P点(2,3).
(1)求a的值和图象的顶点坐标.
(2)点Q(m,n)在该二次函数的图象上.
①当m=﹣2时,求n的值;
②若点Q到y轴的距离小于2,请根据图象直接写出n的取值范围.
4.如图,抛物线y=a(x+1)2的顶点为A,与y轴的负半轴交于点B,且S△AOB=.
(1)求抛物线的解析式;
(2)若点C是该抛物线上A、B两点之间的一点,求△ABC面积的最大值.
5.如图,抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0)两点,与y轴交于点C.点D是抛物线上一个动点,设点D的横坐标为m(1<m<4).连接AC,BC,DB,DC.
(1)求抛物线的函数表达式;
(2)当△BCD的面积等于△AOC的面积的时,求m的值.
6.已知,如图,抛物线y=x2+bx+c经过点A(﹣2,0)和B(0,﹣2).
(1)求此抛物线和直线AB的函数表达式;
(2)点P是直线AB下方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.动点P在什么位置时,△PDE的面积最大?求出面积的最大值,并求出此时点P的坐标.
7.已知二次函数y=ax2+bx+c经过与y轴的交点C(0,5),与x轴相交于点A(﹣1,0)、B(5,0)两点.
(1)求此二次函数的解析式.
(2)如图一,若点M是抛物线上一点,且在直线BC上方,当S△BCM=10时,求点M的坐标.
(3)如图二,点P是抛物线上的任意一点,且在直线BC上方,PQ⊥BC交BC一点Q,求线段PQ的最大值.
8.如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与A重合),过点P作PD∥y轴交直线AC于点D.
(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)△APD能否构成直角三角形?若能,请直接写出所有符合条件的点P坐标;若不能,请说明理由.
9.如图,抛物线y=ax2+bx+c经过坐标原点和点A(﹣4,0),B(﹣1,3).
(1)求抛物线的表达式;
(2)已知抛物线的对称轴为直线l,该抛物线上一点P(m,n)关于直线l的对称点为M,将拋物线沿y轴翻折,点M的对应点为N,请问是否存在点P,使四边形OAPN的面积为20?若存在,判断四边形OAPN的形状,并求点P的坐标;若不存在,请说明理由.
10.如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
(1)求点C的坐标和此抛物线的解析式;
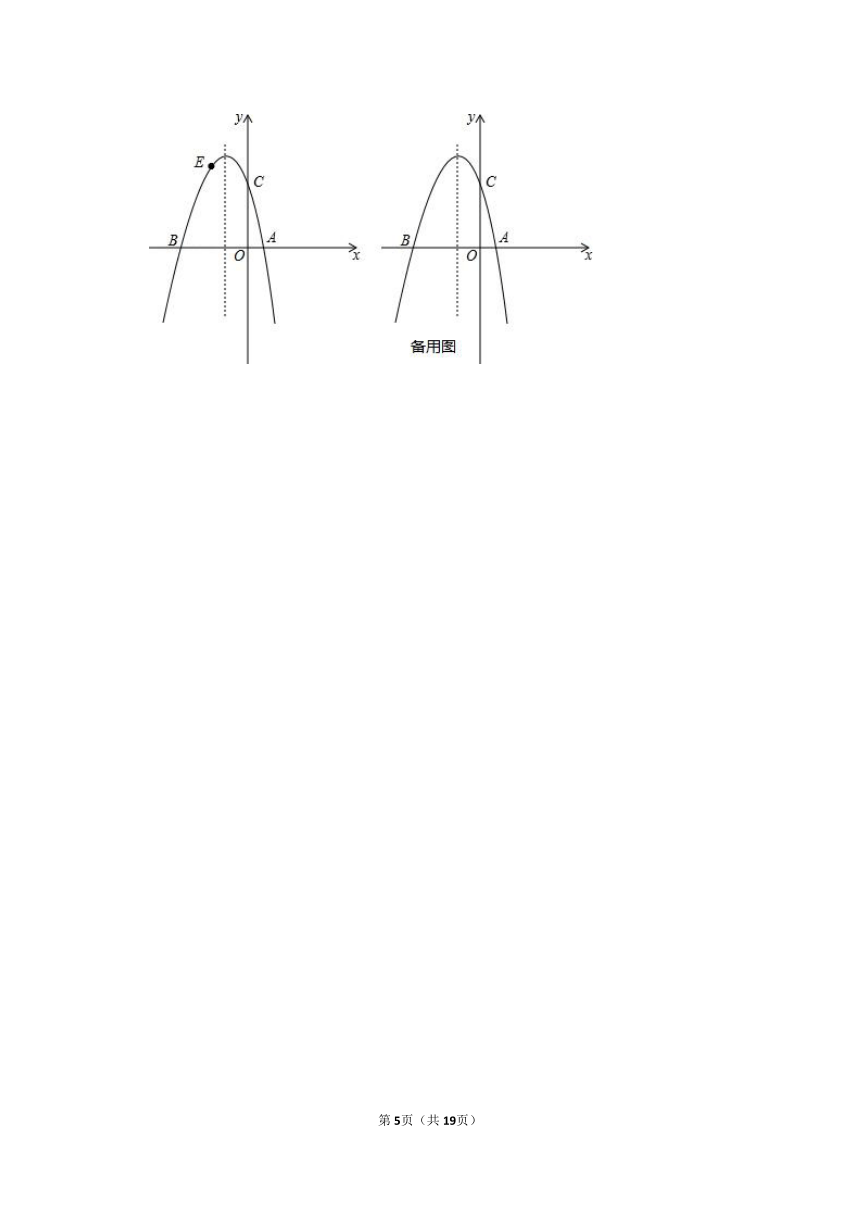
(2)若点E为第二象限抛物线上一动点,连接BE,CE,BC,求△BCE面积的最大值;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
人教版九年级上册第二十二章二次函数22.1.4二次函数的图象和性质
参考答案与试题解析
一.解答题(共10小题)
1.某工厂大门是抛物线形水泥建筑,大门地面宽AB为4m,顶部C距离地面的高度为4.4m,现有一辆货车,其装货宽度为2.4m,高度2.8米,请通过计算说明该货车能否通过此大门?
【解答】解:以C为坐标原点,抛物线的对称轴为y轴,建立如下图所示的平面直角坐标系,
根据题意知,A(﹣2,﹣4.4),B(2,﹣4.4),
设这个函数解析式为y=kx2.
将A的坐标代入,得y=﹣1.1x2,
∵货车装货的宽度为2.4m,
∴E、F两点的横坐标就应该是﹣1.2和1.2,
∴当x=1.2时
y=﹣1.584,
∴GH=CH﹣CG=4.4﹣1.584=2.816(m),
因此这辆汽车装货后的最大高度为2.816m,
∵2.8<2.816,
所以该货车能够通过此大门.
2.如图,已知抛物线y=x2﹣(k+1)x+1的顶点A在x轴的负半轴上,且与一次函数y=﹣x+1交于点B和点C.
(1)求k的值;
(2)求△ABC的面积.
【解答】解;(1)∵抛物线y=x2﹣(k+1)x+1的顶点A在x轴的负半轴上,
∴=0,且﹣<0,
解得,k=﹣3;
(2)∵k=﹣3,
∴抛物线为y=x2+2x+1,
解x2+2x+1=﹣x+1得,x1=0,x2=﹣3,
∴B(﹣3,4),C(0,1),
由直线y=﹣x+1可知与x轴的交点D为(1,0),
∵抛物线为y=x2+2x+1=(x+1)2,
∴A(﹣1,0),
∴AD=2,
∴S△ABC=×2×4﹣=3.
3.如图,已知二次函数y=x2+ax+3的图象经过P点(2,3).
(1)求a的值和图象的顶点坐标.
(2)点Q(m,n)在该二次函数的图象上.
①当m=﹣2时,求n的值;
②若点Q到y轴的距离小于2,请根据图象直接写出n的取值范围.
【解答】解:(1)把点P(2,3)代入y=x2+ax+3中,
∴a=﹣2,
∴y=x2﹣2x+3=(x﹣1)2+2,
∴顶点坐标为(1,2);
(2)①当m=﹣2时,n=(﹣2)2﹣2×(﹣2)+3=11,
②点Q到y轴的距离小于2,
∴|m|<2,
∴﹣2<m<2,
∴2≤n<11.
4.如图,抛物线y=a(x+1)2的顶点为A,与y轴的负半轴交于点B,且S△AOB=.
(1)求抛物线的解析式;
(2)若点C是该抛物线上A、B两点之间的一点,求△ABC面积的最大值.
【解答】解:(1)由题意得:A(﹣1,0),B(0,a),
∴OA=1,OB=﹣a,
∵S△AOB=.
∴=,
解得,a=﹣1,
∴抛物线的解析式为y=﹣(x+1)2;
(2)∵A(﹣1,0),B(0,﹣1),
∴直线AB为y=﹣x﹣1,
过C作CD⊥x轴,交直线AB于点D,
设C(x,﹣(x+1)2),则D(x,﹣x﹣1),
∴CD=﹣(x+1)2+x+1,
∵S△ABC=S△ACD+S△BCD=[﹣(x+1)2+x+1]×1,
∴S△ABC=﹣(x+)2+,
∵﹣<0,
∴△ABC面积的最大值是.
5.如图,抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0)两点,与y轴交于点C.点D是抛物线上一个动点,设点D的横坐标为m(1<m<4).连接AC,BC,DB,DC.
(1)求抛物线的函数表达式;
(2)当△BCD的面积等于△AOC的面积的时,求m的值.
【解答】解:(1))∵抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0)两点,
∴,解之,得:,
∴故抛物线的表达式为:y=﹣x2+x+6;
(2)设直线BC解析式为y=kx+n,
将点B、C的坐标代入得:,解得,
∴直线BC的表达式为:y=﹣x+6,
如图所示,过点D作y轴的平行线交直线BC于点H,
设点D(m,﹣m2+m+6),则点H(m,﹣m+6)
∴S△BDC=HD×OB=(﹣m2+m+6+m﹣6)×4=2(﹣m2+3m),
∵S△ACO=××6×2=,
即:2(﹣m2+3m)=,
解得:m1=3,m2=1(舍去),
故m=3.
6.已知,如图,抛物线y=x2+bx+c经过点A(﹣2,0)和B(0,﹣2).
(1)求此抛物线和直线AB的函数表达式;
(2)点P是直线AB下方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.动点P在什么位置时,△PDE的面积最大?求出面积的最大值,并求出此时点P的坐标.
【解答】解:(1)∵抛物线y=x2+bx+c经过点A(﹣2,0),B(0,﹣2),
∴,
解得:,
所求抛物线的解析式为y=x2+x﹣2;
设直线AB的函数表达式为y=kx+n,
根据题意得,
解得,
所求直线AB的函数表达式为y=﹣x﹣2;
(2)∵A(﹣2,0),B(0,﹣2),
∴OA=OB=2,
∴△AOB是等腰直角三角形,
∴∠BAO=45°,
∵PF⊥x轴,
∴∠AEF=90°﹣45°=45°=∠PED,
又∵PD⊥AB,
∴△PDE是等腰直角三角形,
∴PD2+DE2=PE2,PD=DE,
∴,
∴PE越大,△PDE面积越大.
设点P的坐标为(m,m2+m﹣2),
∴点E坐标为(m,﹣m﹣2),
∴PE=﹣m﹣2﹣(m2+m﹣2)=﹣m2﹣2m=﹣(m+1)2+1(﹣2<m<0),
∵﹣1<0,
∴抛物线开口向下,
∴当m=﹣1时,PE有最大值1,
此时△PDE的面积为==,
当m=﹣1,则m2+m﹣2=1+(﹣1)﹣2=﹣2.
点P坐标为(﹣1,﹣2).
7.已知二次函数y=ax2+bx+c经过与y轴的交点C(0,5),与x轴相交于点A(﹣1,0)、B(5,0)两点.
(1)求此二次函数的解析式.
(2)如图一,若点M是抛物线上一点,且在直线BC上方,当S△BCM=10时,求点M的坐标.
(3)如图二,点P是抛物线上的任意一点,且在直线BC上方,PQ⊥BC交BC一点Q,求线段PQ的最大值.
【解答】解:(1)将点A、B、C的坐标代入抛物线表达式得,解得,
故抛物线的表达式为y=﹣x2+4x+5;
(2)过点M作MH∥y轴交BC于点H,
由点B、C的坐标得,直线BC的表达式为y=﹣x+5,
设点M的坐标为(x,﹣x2+4x+5),则点H(x,﹣x+5),
则MH=﹣x2+4x+5﹣(﹣x+5)=﹣x2+5x,
则S△BCM=S△MHB+S△MHC=×MH×OB=×(﹣x2+5x)×5=10,
解得x=1或4,
故点M的坐标为(1,8)或(4,5);
(3)过点P作PH∥y轴交BC于点H,
∵OB=OC=5,故直线BC与x轴负半轴的夹角为45°,则∠PHC=45°,
由(2)知,PH=MH=﹣x2+5x,
故PQ=PH=(﹣x2+5x),
∵<0.故PQ有最大值,当x=时,PQ的最大值为.
8.如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与A重合),过点P作PD∥y轴交直线AC于点D.
(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)△APD能否构成直角三角形?若能,请直接写出所有符合条件的点P坐标;若不能,请说明理由.
【解答】解:(1)∵抛物线y=x2+bx+c过点A(3,0),B(1,0),
∴,
解得,
∴抛物线解析式为y=x2﹣4x+3;
(2)令x=0,则y=3,
∴点C(0,3),
则直线AC的解析式为y=﹣x+3,
设点P(x,x2﹣4x+3),
∵PD∥y轴,
∴点D(x,﹣x+3),
∴PD=(﹣x+3)﹣(x2﹣4x+3)=﹣x2+3x=﹣(x﹣)2+,
∵a=﹣1<0,
∴当x=时,线段PD的长度有最大值;
(3)①∠APD是直角时,点P与点B重合,
此时,点P(1,0),
②∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的顶点坐标为(2,﹣1),
∵A(3,0),
∴点P为在抛物线顶点时,∠PAD=45°+45°=90°,
此时,点P(2,﹣1),
综上所述,点P(1,0)或(2,﹣1)时,△APD能构成直角三角形.
9.如图,抛物线y=ax2+bx+c经过坐标原点和点A(﹣4,0),B(﹣1,3).
(1)求抛物线的表达式;
(2)已知抛物线的对称轴为直线l,该抛物线上一点P(m,n)关于直线l的对称点为M,将拋物线沿y轴翻折,点M的对应点为N,请问是否存在点P,使四边形OAPN的面积为20?若存在,判断四边形OAPN的形状,并求点P的坐标;若不存在,请说明理由.
【解答】解:(1)∵抛物线y=ax2+bx+c经过坐标原点和点A(﹣4,0),B(﹣1,3),
∴,
解得:a=﹣1,b=﹣4,c=0,
故此二次函数的解析式为y=﹣x2﹣4x;
(2)如图所示:
由题可知,M、N点坐标分别为(﹣4﹣m,n),(m+4,n),
∴PN∥OA,PN=|m﹣(m+4)=4,
∵OA=4,
∴PN=OA,
∴四边形OAPN是平行四边形,
∵四边形OAPN的面积=(OA+NP)÷2×|n|=20,
即4|n|=20,
∴|n|=5.
∴n=±5,
所以﹣m2﹣4m=±5,
当﹣m2﹣4m=5,即m2+4m+5=0时,
∵△=16﹣20<0,不存在,
当﹣m2﹣4m=﹣5时,
解得m=﹣5或m=1.
∴P(﹣5,﹣5)或(1,﹣5).
10.如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
(1)求点C的坐标和此抛物线的解析式;
(2)若点E为第二象限抛物线上一动点,连接BE,CE,BC,求△BCE面积的最大值;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
【解答】解:(1)∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),
∴OB=3,
∵OC=OB,
∴OC=3,
∴c=3,
∴,
解得:,
∴所求抛物线解析式为:y=﹣x2﹣2x+3,C(0,3).
(2)如图2,连接BC,过点E作EF⊥x轴于点F,设E(a,﹣a2﹣2a+3)(﹣3<a<0),
∴EF=﹣a2﹣2a+3,BF=a+3,OF=﹣a,
∴S△BEC=S四边形BOCE﹣S△BOC=BF?EF+(OC+EF)?OF﹣?OB?OC
=(a+3)?(﹣a2﹣2a+3)+(﹣a2﹣2a+6)?(﹣a)﹣
=﹣a2﹣a
=﹣(a+)2+,
∴当a=﹣时,S△BEC最大,且最大值为.
(3)∵抛物线y=﹣x2﹣2x+3的对称轴为x=﹣1,点P在抛物线的对称轴上,
∴设P(﹣1,m),
∵线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,
①当m≥0时,
∴PA=PA′,∠APA′=90°,
如图3,过A′作A′N⊥对称轴于N,设对称轴于x轴交于点M,
∴∠NPA′+∠MPA=∠NA′P+∠NPA′=90°,
∴∠NA′P=∠NPA,
在△A′NP与△PMA中,
,
∴△A′NP≌△PMA(AAS),
∴A′N=PM=m,PN=AM=2,
∴A′(m﹣1,m+2),
代入y=﹣x2﹣2x+3得:m+2=﹣(m﹣1)2﹣2(m﹣1)+3,
解得:m=1,m=﹣2(舍去),
②当m<0时,要使P2A=P2A2,由图可知A2点与B点重合,
∵∠AP2A2=90°,
∴MP2=MA=2,
∴P2(﹣1,﹣2),
点P2关于x轴的对称点P3(﹣1,2)也满足条件,
∴满足条件的点P的坐标为P(﹣1,1)或(﹣1,﹣2)或(﹣1,2).
第2页(共2页)
一.解答题(共10小题)
1.某工厂大门是抛物线形水泥建筑,大门地面宽AB为4m,顶部C距离地面的高度为4.4m,现有一辆货车,其装货宽度为2.4m,高度2.8米,请通过计算说明该货车能否通过此大门?
2.如图,已知抛物线y=x2﹣(k+1)x+1的顶点A在x轴的负半轴上,且与一次函数y=﹣x+1交于点B和点C.
(1)求k的值;
(2)求△ABC的面积.
3.如图,已知二次函数y=x2+ax+3的图象经过P点(2,3).
(1)求a的值和图象的顶点坐标.
(2)点Q(m,n)在该二次函数的图象上.
①当m=﹣2时,求n的值;
②若点Q到y轴的距离小于2,请根据图象直接写出n的取值范围.
4.如图,抛物线y=a(x+1)2的顶点为A,与y轴的负半轴交于点B,且S△AOB=.
(1)求抛物线的解析式;
(2)若点C是该抛物线上A、B两点之间的一点,求△ABC面积的最大值.
5.如图,抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0)两点,与y轴交于点C.点D是抛物线上一个动点,设点D的横坐标为m(1<m<4).连接AC,BC,DB,DC.
(1)求抛物线的函数表达式;
(2)当△BCD的面积等于△AOC的面积的时,求m的值.
6.已知,如图,抛物线y=x2+bx+c经过点A(﹣2,0)和B(0,﹣2).
(1)求此抛物线和直线AB的函数表达式;
(2)点P是直线AB下方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.动点P在什么位置时,△PDE的面积最大?求出面积的最大值,并求出此时点P的坐标.
7.已知二次函数y=ax2+bx+c经过与y轴的交点C(0,5),与x轴相交于点A(﹣1,0)、B(5,0)两点.
(1)求此二次函数的解析式.
(2)如图一,若点M是抛物线上一点,且在直线BC上方,当S△BCM=10时,求点M的坐标.
(3)如图二,点P是抛物线上的任意一点,且在直线BC上方,PQ⊥BC交BC一点Q,求线段PQ的最大值.
8.如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与A重合),过点P作PD∥y轴交直线AC于点D.
(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)△APD能否构成直角三角形?若能,请直接写出所有符合条件的点P坐标;若不能,请说明理由.
9.如图,抛物线y=ax2+bx+c经过坐标原点和点A(﹣4,0),B(﹣1,3).
(1)求抛物线的表达式;
(2)已知抛物线的对称轴为直线l,该抛物线上一点P(m,n)关于直线l的对称点为M,将拋物线沿y轴翻折,点M的对应点为N,请问是否存在点P,使四边形OAPN的面积为20?若存在,判断四边形OAPN的形状,并求点P的坐标;若不存在,请说明理由.
10.如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
(1)求点C的坐标和此抛物线的解析式;
(2)若点E为第二象限抛物线上一动点,连接BE,CE,BC,求△BCE面积的最大值;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
人教版九年级上册第二十二章二次函数22.1.4二次函数的图象和性质
参考答案与试题解析
一.解答题(共10小题)
1.某工厂大门是抛物线形水泥建筑,大门地面宽AB为4m,顶部C距离地面的高度为4.4m,现有一辆货车,其装货宽度为2.4m,高度2.8米,请通过计算说明该货车能否通过此大门?
【解答】解:以C为坐标原点,抛物线的对称轴为y轴,建立如下图所示的平面直角坐标系,
根据题意知,A(﹣2,﹣4.4),B(2,﹣4.4),
设这个函数解析式为y=kx2.
将A的坐标代入,得y=﹣1.1x2,
∵货车装货的宽度为2.4m,
∴E、F两点的横坐标就应该是﹣1.2和1.2,
∴当x=1.2时
y=﹣1.584,
∴GH=CH﹣CG=4.4﹣1.584=2.816(m),
因此这辆汽车装货后的最大高度为2.816m,
∵2.8<2.816,
所以该货车能够通过此大门.
2.如图,已知抛物线y=x2﹣(k+1)x+1的顶点A在x轴的负半轴上,且与一次函数y=﹣x+1交于点B和点C.
(1)求k的值;
(2)求△ABC的面积.
【解答】解;(1)∵抛物线y=x2﹣(k+1)x+1的顶点A在x轴的负半轴上,
∴=0,且﹣<0,
解得,k=﹣3;
(2)∵k=﹣3,
∴抛物线为y=x2+2x+1,
解x2+2x+1=﹣x+1得,x1=0,x2=﹣3,
∴B(﹣3,4),C(0,1),
由直线y=﹣x+1可知与x轴的交点D为(1,0),
∵抛物线为y=x2+2x+1=(x+1)2,
∴A(﹣1,0),
∴AD=2,
∴S△ABC=×2×4﹣=3.
3.如图,已知二次函数y=x2+ax+3的图象经过P点(2,3).
(1)求a的值和图象的顶点坐标.
(2)点Q(m,n)在该二次函数的图象上.
①当m=﹣2时,求n的值;
②若点Q到y轴的距离小于2,请根据图象直接写出n的取值范围.
【解答】解:(1)把点P(2,3)代入y=x2+ax+3中,
∴a=﹣2,
∴y=x2﹣2x+3=(x﹣1)2+2,
∴顶点坐标为(1,2);
(2)①当m=﹣2时,n=(﹣2)2﹣2×(﹣2)+3=11,
②点Q到y轴的距离小于2,
∴|m|<2,
∴﹣2<m<2,
∴2≤n<11.
4.如图,抛物线y=a(x+1)2的顶点为A,与y轴的负半轴交于点B,且S△AOB=.
(1)求抛物线的解析式;
(2)若点C是该抛物线上A、B两点之间的一点,求△ABC面积的最大值.
【解答】解:(1)由题意得:A(﹣1,0),B(0,a),
∴OA=1,OB=﹣a,
∵S△AOB=.
∴=,
解得,a=﹣1,
∴抛物线的解析式为y=﹣(x+1)2;
(2)∵A(﹣1,0),B(0,﹣1),
∴直线AB为y=﹣x﹣1,
过C作CD⊥x轴,交直线AB于点D,
设C(x,﹣(x+1)2),则D(x,﹣x﹣1),
∴CD=﹣(x+1)2+x+1,
∵S△ABC=S△ACD+S△BCD=[﹣(x+1)2+x+1]×1,
∴S△ABC=﹣(x+)2+,
∵﹣<0,
∴△ABC面积的最大值是.
5.如图,抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0)两点,与y轴交于点C.点D是抛物线上一个动点,设点D的横坐标为m(1<m<4).连接AC,BC,DB,DC.
(1)求抛物线的函数表达式;
(2)当△BCD的面积等于△AOC的面积的时,求m的值.
【解答】解:(1))∵抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0)两点,
∴,解之,得:,
∴故抛物线的表达式为:y=﹣x2+x+6;
(2)设直线BC解析式为y=kx+n,
将点B、C的坐标代入得:,解得,
∴直线BC的表达式为:y=﹣x+6,
如图所示,过点D作y轴的平行线交直线BC于点H,
设点D(m,﹣m2+m+6),则点H(m,﹣m+6)
∴S△BDC=HD×OB=(﹣m2+m+6+m﹣6)×4=2(﹣m2+3m),
∵S△ACO=××6×2=,
即:2(﹣m2+3m)=,
解得:m1=3,m2=1(舍去),
故m=3.
6.已知,如图,抛物线y=x2+bx+c经过点A(﹣2,0)和B(0,﹣2).
(1)求此抛物线和直线AB的函数表达式;
(2)点P是直线AB下方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.动点P在什么位置时,△PDE的面积最大?求出面积的最大值,并求出此时点P的坐标.
【解答】解:(1)∵抛物线y=x2+bx+c经过点A(﹣2,0),B(0,﹣2),
∴,
解得:,
所求抛物线的解析式为y=x2+x﹣2;
设直线AB的函数表达式为y=kx+n,
根据题意得,
解得,
所求直线AB的函数表达式为y=﹣x﹣2;
(2)∵A(﹣2,0),B(0,﹣2),
∴OA=OB=2,
∴△AOB是等腰直角三角形,
∴∠BAO=45°,
∵PF⊥x轴,
∴∠AEF=90°﹣45°=45°=∠PED,
又∵PD⊥AB,
∴△PDE是等腰直角三角形,
∴PD2+DE2=PE2,PD=DE,
∴,
∴PE越大,△PDE面积越大.
设点P的坐标为(m,m2+m﹣2),
∴点E坐标为(m,﹣m﹣2),
∴PE=﹣m﹣2﹣(m2+m﹣2)=﹣m2﹣2m=﹣(m+1)2+1(﹣2<m<0),
∵﹣1<0,
∴抛物线开口向下,
∴当m=﹣1时,PE有最大值1,
此时△PDE的面积为==,
当m=﹣1,则m2+m﹣2=1+(﹣1)﹣2=﹣2.
点P坐标为(﹣1,﹣2).
7.已知二次函数y=ax2+bx+c经过与y轴的交点C(0,5),与x轴相交于点A(﹣1,0)、B(5,0)两点.
(1)求此二次函数的解析式.
(2)如图一,若点M是抛物线上一点,且在直线BC上方,当S△BCM=10时,求点M的坐标.
(3)如图二,点P是抛物线上的任意一点,且在直线BC上方,PQ⊥BC交BC一点Q,求线段PQ的最大值.
【解答】解:(1)将点A、B、C的坐标代入抛物线表达式得,解得,
故抛物线的表达式为y=﹣x2+4x+5;
(2)过点M作MH∥y轴交BC于点H,
由点B、C的坐标得,直线BC的表达式为y=﹣x+5,
设点M的坐标为(x,﹣x2+4x+5),则点H(x,﹣x+5),
则MH=﹣x2+4x+5﹣(﹣x+5)=﹣x2+5x,
则S△BCM=S△MHB+S△MHC=×MH×OB=×(﹣x2+5x)×5=10,
解得x=1或4,
故点M的坐标为(1,8)或(4,5);
(3)过点P作PH∥y轴交BC于点H,
∵OB=OC=5,故直线BC与x轴负半轴的夹角为45°,则∠PHC=45°,
由(2)知,PH=MH=﹣x2+5x,
故PQ=PH=(﹣x2+5x),
∵<0.故PQ有最大值,当x=时,PQ的最大值为.
8.如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与A重合),过点P作PD∥y轴交直线AC于点D.
(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)△APD能否构成直角三角形?若能,请直接写出所有符合条件的点P坐标;若不能,请说明理由.
【解答】解:(1)∵抛物线y=x2+bx+c过点A(3,0),B(1,0),
∴,
解得,
∴抛物线解析式为y=x2﹣4x+3;
(2)令x=0,则y=3,
∴点C(0,3),
则直线AC的解析式为y=﹣x+3,
设点P(x,x2﹣4x+3),
∵PD∥y轴,
∴点D(x,﹣x+3),
∴PD=(﹣x+3)﹣(x2﹣4x+3)=﹣x2+3x=﹣(x﹣)2+,
∵a=﹣1<0,
∴当x=时,线段PD的长度有最大值;
(3)①∠APD是直角时,点P与点B重合,
此时,点P(1,0),
②∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的顶点坐标为(2,﹣1),
∵A(3,0),
∴点P为在抛物线顶点时,∠PAD=45°+45°=90°,
此时,点P(2,﹣1),
综上所述,点P(1,0)或(2,﹣1)时,△APD能构成直角三角形.
9.如图,抛物线y=ax2+bx+c经过坐标原点和点A(﹣4,0),B(﹣1,3).
(1)求抛物线的表达式;
(2)已知抛物线的对称轴为直线l,该抛物线上一点P(m,n)关于直线l的对称点为M,将拋物线沿y轴翻折,点M的对应点为N,请问是否存在点P,使四边形OAPN的面积为20?若存在,判断四边形OAPN的形状,并求点P的坐标;若不存在,请说明理由.
【解答】解:(1)∵抛物线y=ax2+bx+c经过坐标原点和点A(﹣4,0),B(﹣1,3),
∴,
解得:a=﹣1,b=﹣4,c=0,
故此二次函数的解析式为y=﹣x2﹣4x;
(2)如图所示:
由题可知,M、N点坐标分别为(﹣4﹣m,n),(m+4,n),
∴PN∥OA,PN=|m﹣(m+4)=4,
∵OA=4,
∴PN=OA,
∴四边形OAPN是平行四边形,
∵四边形OAPN的面积=(OA+NP)÷2×|n|=20,
即4|n|=20,
∴|n|=5.
∴n=±5,
所以﹣m2﹣4m=±5,
当﹣m2﹣4m=5,即m2+4m+5=0时,
∵△=16﹣20<0,不存在,
当﹣m2﹣4m=﹣5时,
解得m=﹣5或m=1.
∴P(﹣5,﹣5)或(1,﹣5).
10.如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
(1)求点C的坐标和此抛物线的解析式;
(2)若点E为第二象限抛物线上一动点,连接BE,CE,BC,求△BCE面积的最大值;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
【解答】解:(1)∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),
∴OB=3,
∵OC=OB,
∴OC=3,
∴c=3,
∴,
解得:,
∴所求抛物线解析式为:y=﹣x2﹣2x+3,C(0,3).
(2)如图2,连接BC,过点E作EF⊥x轴于点F,设E(a,﹣a2﹣2a+3)(﹣3<a<0),
∴EF=﹣a2﹣2a+3,BF=a+3,OF=﹣a,
∴S△BEC=S四边形BOCE﹣S△BOC=BF?EF+(OC+EF)?OF﹣?OB?OC
=(a+3)?(﹣a2﹣2a+3)+(﹣a2﹣2a+6)?(﹣a)﹣
=﹣a2﹣a
=﹣(a+)2+,
∴当a=﹣时,S△BEC最大,且最大值为.
(3)∵抛物线y=﹣x2﹣2x+3的对称轴为x=﹣1,点P在抛物线的对称轴上,
∴设P(﹣1,m),
∵线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,
①当m≥0时,
∴PA=PA′,∠APA′=90°,
如图3,过A′作A′N⊥对称轴于N,设对称轴于x轴交于点M,
∴∠NPA′+∠MPA=∠NA′P+∠NPA′=90°,
∴∠NA′P=∠NPA,
在△A′NP与△PMA中,
,
∴△A′NP≌△PMA(AAS),
∴A′N=PM=m,PN=AM=2,
∴A′(m﹣1,m+2),
代入y=﹣x2﹣2x+3得:m+2=﹣(m﹣1)2﹣2(m﹣1)+3,
解得:m=1,m=﹣2(舍去),
②当m<0时,要使P2A=P2A2,由图可知A2点与B点重合,
∵∠AP2A2=90°,
∴MP2=MA=2,
∴P2(﹣1,﹣2),
点P2关于x轴的对称点P3(﹣1,2)也满足条件,
∴满足条件的点P的坐标为P(﹣1,1)或(﹣1,﹣2)或(﹣1,2).
第2页(共2页)
同课章节目录
