人教版 九年级数学上册 24.2 点和圆、直线和圆的位置关系 同步课时训练(Word版 含答案)
文档属性
| 名称 | 人教版 九年级数学上册 24.2 点和圆、直线和圆的位置关系 同步课时训练(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 628.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-27 22:01:05 | ||
图片预览




文档简介
人教版
九年级数学上册
24.2
点和圆、直线和圆的位置关系
同步课时训练
一、选择题(本大题共10道小题)
1.
下列说法中,正确的是( )
A.垂直于半径的直线是圆的切线
B.经过半径的外端且垂直于这条半径的直线是圆的切线
C.经过半径的端点且垂直于这条半径的直线是圆的切线
D.到圆心的距离等于直径的直线是圆的切线
2.
如图,AB是⊙O的直径,MN是⊙O的切线,切点为N,如果∠MNB=52°,则∠NOA的度数为( )
A.76°
B.56°
C.54°
D.52°
3.
2018·舟山
用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是( )
A.点在圆内
B.点在圆上
C.点在圆心上
D.点在圆上或圆内
4.
平面上⊙O与四条直线l1,l2,l3,l4的位置关系如图.若⊙O的半径为2
cm,且点O到其中一条直线的距离为2.2
cm,则这条直线是( )
A.ll
B.l2
C.l3
D.l4
5.
如图,在正三角形网格中,△ABC的顶点都在格点上,点P,Q,M是AB与网格线的交点,则△ABC的外心是( )
A.点P
B.点Q
C.点M
D.点N
6.
如图,数轴上有A,B,C三点,点A,C关于点B对称,以原点O为圆心作圆,若点A,B,C分别在⊙O外、⊙O内、⊙O上,则原点O的位置应该在( )
图
A.点A与点B之间靠近点A
B.点A与点B之间靠近点B
C.点B与点C之间靠近点B
D.点B与点C之间靠近点C
7.
如图,一个边长为4
cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则CE的长为( )
A.4
cm
B.3
cm
C.2
cm
D.1.5
cm
8.
如图,⊙C的半径为1,圆心的坐标为(3,4),P(m,n)是⊙C内或⊙C上的一个动点,则m2+n2的最小值是( )
A.9
B.16
C.25
D.36
9.
2020·武汉模拟
在平面直角坐标系中,圆心为坐标原点,⊙O的半径为10,则P(-10,1)与⊙O的位置关系为( )
A.点P在⊙O上
B.点P在⊙O外
C.点P在⊙O内
D.无法确定
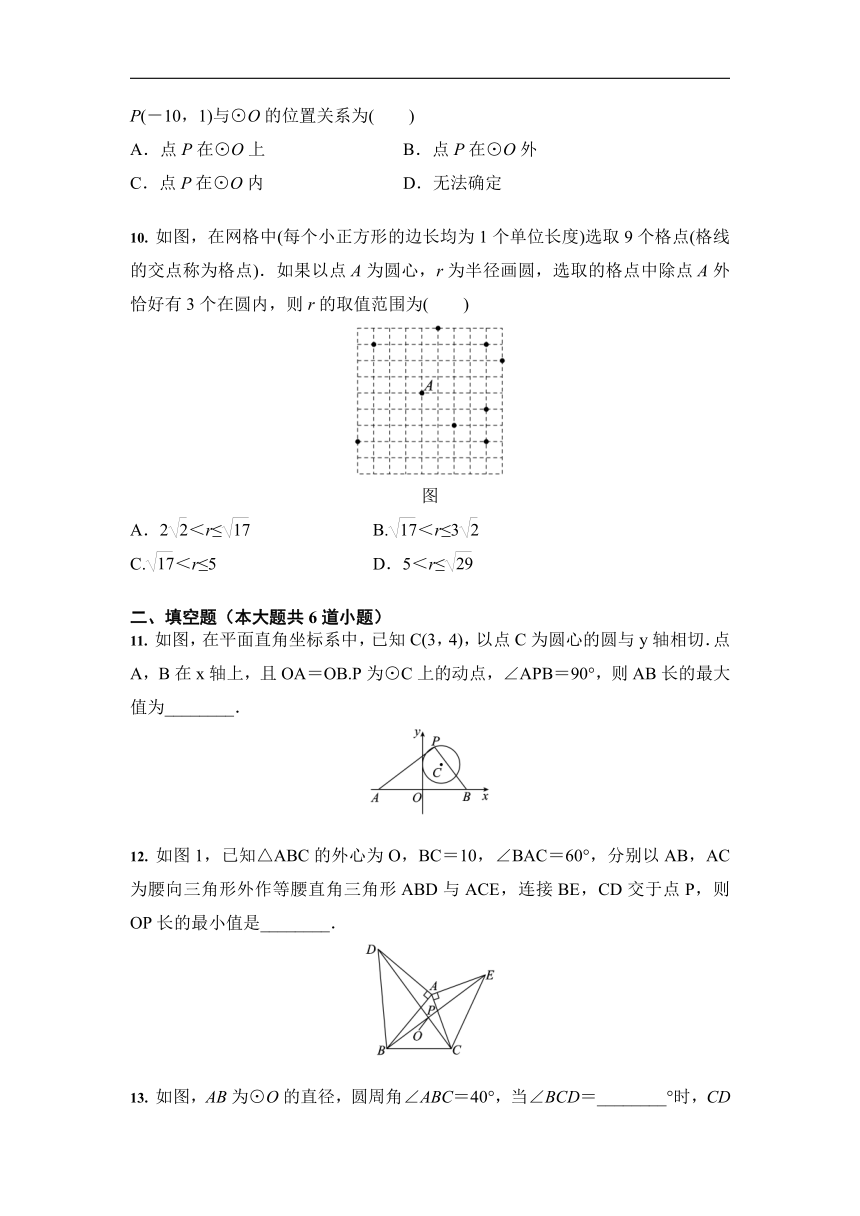
10.
如图,在网格中(每个小正方形的边长均为1个单位长度)选取9个格点(格线的交点称为格点).如果以点A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
图
A.2<r≤
B.<r≤3
C.<r≤5
D.5<r≤
二、填空题(本大题共6道小题)
11.
如图,在平面直角坐标系中,已知C(3,4),以点C为圆心的圆与y轴相切.点A,B在x轴上,且OA=OB.P为⊙C上的动点,∠APB=90°,则AB长的最大值为________.
12.
如图1,已知△ABC的外心为O,BC=10,∠BAC=60°,分别以AB,AC为腰向三角形外作等腰直角三角形ABD与ACE,连接BE,CD交于点P,则OP长的最小值是________.
13.
如图,AB为⊙O的直径,圆周角∠ABC=40°,当∠BCD=________°时,CD为⊙O的切线.
14.
如图,⊙M的圆心在一次函数y=x+2的图象上运动,半径为1.当⊙M与y轴相切时,点M的坐标为__________.
15.
如图所示,在半圆O中,AB是直径,D是半圆O上一点,C是的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,有下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心.其中正确的结论是________(只需填写序号).
16.
如图,半圆的圆心O与坐标原点重合,半圆的半径为1,直线l的解析式为y=x+t.若直线l与半圆只有一个公共点,则t的取值范围是________.
三、解答题(本大题共4道小题)
17.
2018·邵阳
如图所示,AB是⊙O的直径,C为⊙O上一点,过点B作BD⊥CD,垂足为D,连接BC,BC平分∠ABD.
求证:CD为⊙O的切线.
18.
2019·天津
如图,已知PA,PB分别与⊙O相切于点A,B,∠APB=80°,C为⊙O上一点.
(1)如图①,求∠ACB的大小;
(2)如图②,AE为⊙O的直径,AE与BC相交于点D.若AB=AD,求∠EAC的大小.
19.
如图①,直线PA交⊙O于A,E两点,PA的垂线CD切⊙O于点C,交PA于点D,过点A作⊙O的直径AB.
(1)求证:AC平分∠DAB;
(2)如图②,将直线CD向下平行移动,得到CD与⊙O相切于点C,AC还平分∠DAB吗?请说明理由.
解题突破(20题)
在动态情况下,探究结论是否发生变化,主要看使结论成立的主要条件是否改变.比如本题中虽然图形发生变化,但AD和OC平行,△AOC是等腰三角形这两个主要条件没有改变,因此结论不发生变化.
20.
如图,AB是⊙O的直径,AB=8,点C在⊙O的半径OA上运动,PC⊥AB,垂足为C,PC=5,PT为⊙O的切线,切点为T.
(1)如图①,当点C运动到点O时,求PT的长;
(2)如图②,当点C运动到点A时,连接PO,BT,求证:PO∥BT;
(3)如图③,设PT2=y,AC=x,求y与x之间的函数解析式及y的最小值.
人教版
九年级数学上册
24.2
点和圆、直线和圆的位置关系
同步课时训练-答案
一、选择题(本大题共10道小题)
1.
【答案】B
2.
【答案】A [解析]
∵MN是⊙O的切线,∴ON⊥NM,∴∠ONM=90°,
∴∠ONB=90°-∠MNB=90°-52°=38°.
∵ON=OB,∴∠B=∠ONB=38°,∴∠NOA=2∠B=76°.
3.
【答案】D
4.
【答案】C [解析]
因为所求直线到圆心O的距离为2.2
cm>半径2
cm,所以此直线与⊙O相离,所以这条直线为直线l3.
5.
【答案】B [解析]
由题意可知∠BCN=60°,∠ACN=30°,∴∠ACB=∠ACN+∠BCN=90°,
∴△ABC是直角三角形,
∴△ABC的外心是斜边AB的中点.
∵Q是AB的中点,
∴△ABC的外心是点Q.
6.
【答案】C [解析]
如图.
7.
【答案】B [解析]
如图,连接OC,并过点O作OF⊥CE于点F.
∵△ABC为等边三角形,边长为4
cm,
∴△ABC的高为2
cm,∴OC=
cm.
又∵⊙O与BC相切于点C,∠ACB=60°,
∴∠OCF=30°.
在Rt△OFC中,可得FC=
cm,
∴CE=2FC=3
cm.
8.
【答案】B [解析]
如图,连接OC交⊙C于点P′.
∵圆心C的坐标为(3,4),点P的坐标为(m,n),
∴OC=5,OP=,
∴m2+n2是点P到原点的距离的平方,
∴当点P运动到线段OC上,即点P′处时,点P离原点最近,即m2+n2取得最小值,
此时OP=OC-PC=5-1=4,即m2+n2=16.
9.
【答案】B
10.
【答案】B [解析]
如图,∵AD=2
,AE=AF=,AB=3
,
∴AB>AE=AF>AD,
∴当<r<3
时,以点A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内.
二、填空题(本大题共6道小题)
11.
【答案】16
12.
【答案】5- [解析]
∵∠BAD=∠CAE=90°,
∴∠DAC=∠BAE.
在△DAC和△BAE中,
∴△DAC≌△BAE(SAS),
∴∠ADC=∠ABE,
从而∠PDB+∠PBD=90°,
即∠DPB=90°,从而∠BPC=90°,
∴点P在以BC为直径的圆上.
如图,过点O作OH⊥BC于点H,连接OB,OC.
∵△ABC的外心为O,∠BAC=60°,
∴∠BOC=120°.又∵BC=10,
∴OH=
,∴OP长的最小值是5- .
13.
【答案】50 [解析]
连接OC.
∵OC=OB,∴∠OCB=∠ABC=40°.
∵∠BCD=50°,∴∠OCD=90°,
∴CD为⊙O的切线.
14.
【答案】(1,)或(-1,) [解析]
∵⊙M的圆心在一次函数y=x+2的图象上运动,∴设当⊙M与y轴相切时圆心M的坐标为(x,x+2).∵⊙M的半径为1,∴x=1或x=-1,当x=1时,y=,当x=-1时,y=.∴点M的坐标为(1,)或(-1,).
15.
【答案】②③ [解析]
∵在半圆O中,AB是直径,D是半圆O上一点,C是的中点,
∴=,但不一定等于,
∴∠BAD与∠ABC不一定相等,故①错误.
如图,连接OD,则OD⊥GD,∠OAD=∠ODA.
∵∠ODA+∠GDP=90°,∠OAD+∠GPD=∠OAD+∠APE=90°,
∴∠GPD=∠GDP,∴GP=GD,故②正确.
补全⊙O,延长CE交⊙O于点F.
∵CE⊥AB,∴A为的中点,即=.
又∵C为的中点,∴=,∴=,
∴∠CAP=∠ACP,∴AP=CP.
∵AB为⊙O的直径,∴∠ACQ=90°,
∴∠ACP+∠PCQ=90°,∠CAP+∠PQC=90°,
∴∠PCQ=∠PQC,∴PC=PQ,
∴AP=PQ,即P为Rt△ACQ的斜边AQ的中点,
∴点P为Rt△ACQ的外心,故③正确.
16.
【答案】t=或-1≤t<1 [解析]
若直线与半圆只有一个公共点,则有两种情况:直线和半圆相切于点C或从直线过点A开始到直线过点B结束(不包括直线过点A).
直线y=x+t与x轴所形成的锐角是45°.
当点O到直线l的距离OC=1时,直线l与半圆O相切,设直线l与y轴交于点D,则OD=,即t=.
当直线过点A时,把A(-1,0)代入直线l的解析式,得t=y-x=1.
当直线过点B时,把B(1,0)代入直线l的解析式,得t=y-x=-1.
即当t=或-1≤t<1时,直线和半圆只有一个公共点.
故答案为t=或-1≤t<1.
三、解答题(本大题共4道小题)
17.
【答案】
证明:连接OC.∵BC平分∠ABD,
∴∠OBC=∠DBC.
∵OB=OC,∴∠OBC=∠OCB,
∴∠OCB=∠DBC,
∴OC∥BD.
∵BD⊥CD,∴OC⊥CD,∴CD为⊙O的切线.
18.
【答案】
解:(1)如图①,连接OA,OB,
∵PA,PB是⊙O的切线,
∴∠OAP=∠OBP=90°,
∴∠AOB=360°-90°-90°-80°=100°.
由圆周角定理,得∠ACB=∠AOB=50°.
(2)如图②,连接CE.
∵AE为⊙O的直径,
∴∠ACE=90°.
∵∠ACB=50°,
∴∠BCE=90°-50°=40°,
∴∠BAE=∠BCE=40°.
∵AB=AD,
∴∠ABD=∠ADB=70°,
∴∠EAC=∠ADB-∠ACB=20°.
19.
【答案】
解:(1)证明:连接OC.
∵OA=OC,∴∠OAC=∠OCA.
∵CD切⊙O于点C,∴CD⊥OC.
又∵CD⊥PA,∴OC∥PA,∴∠PAC=∠OCA,
∴∠OAC=∠PAC,即AC平分∠DAB.
(2)AC还平分∠DAB.理由:连接OC.
∵CD切⊙O于点C,∴CD⊥OC.
又∵AD⊥CD,∴OC∥AD,
∴∠OCA=∠DAC.
又∵OA=OC,
∴∠OAC=∠OCA,
∴∠DAC=∠OAC,
即AC平分∠DAB.
20.
【答案】
解:(1)连接OT.
∵PT为⊙O的切线,∴OT⊥PT,
∴在Rt△PTO中,PT==3.
(2)证明:连接AT,OT.
∵PT为⊙O的切线,
∴PT⊥OT,
∴∠PTO=90°=∠PAO.
在Rt△PAO和Rt△PTO中,
∵PO=PO,OA=OT,
∴Rt△PAO≌Rt△PTO,
∴PA=PT,∠APO=∠TPO,∴PO⊥AT.
∵AB是⊙O的直径,
∴∠ATB是直角,即BT⊥AT,∴PO∥BT.
(3)连接PO,OT.
∵PT为⊙O的切线,∴PT⊥OT.
∵AC=x,∴CO=OA-AC=4-x.
在Rt△PCO中,PO2=PC2+CO2=52+(4-x)2.
在Rt△POT中,PO2=PT2+OT2=PT2+42,
∴PT2+42=52+(4-x)2,
即y+42=52+(4-x)2,
∴y=9+(4-x)2=x2-8x+25=(x-4)2+9(0≤x≤4),
∴当x=4时,y有最小值9.
∴y与x之间的函数解析式为y=x2-8x+25(0≤x≤4),y的最小值是9.
九年级数学上册
24.2
点和圆、直线和圆的位置关系
同步课时训练
一、选择题(本大题共10道小题)
1.
下列说法中,正确的是( )
A.垂直于半径的直线是圆的切线
B.经过半径的外端且垂直于这条半径的直线是圆的切线
C.经过半径的端点且垂直于这条半径的直线是圆的切线
D.到圆心的距离等于直径的直线是圆的切线
2.
如图,AB是⊙O的直径,MN是⊙O的切线,切点为N,如果∠MNB=52°,则∠NOA的度数为( )
A.76°
B.56°
C.54°
D.52°
3.
2018·舟山
用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是( )
A.点在圆内
B.点在圆上
C.点在圆心上
D.点在圆上或圆内
4.
平面上⊙O与四条直线l1,l2,l3,l4的位置关系如图.若⊙O的半径为2
cm,且点O到其中一条直线的距离为2.2
cm,则这条直线是( )
A.ll
B.l2
C.l3
D.l4
5.
如图,在正三角形网格中,△ABC的顶点都在格点上,点P,Q,M是AB与网格线的交点,则△ABC的外心是( )
A.点P
B.点Q
C.点M
D.点N
6.
如图,数轴上有A,B,C三点,点A,C关于点B对称,以原点O为圆心作圆,若点A,B,C分别在⊙O外、⊙O内、⊙O上,则原点O的位置应该在( )
图
A.点A与点B之间靠近点A
B.点A与点B之间靠近点B
C.点B与点C之间靠近点B
D.点B与点C之间靠近点C
7.
如图,一个边长为4
cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则CE的长为( )
A.4
cm
B.3
cm
C.2
cm
D.1.5
cm
8.
如图,⊙C的半径为1,圆心的坐标为(3,4),P(m,n)是⊙C内或⊙C上的一个动点,则m2+n2的最小值是( )
A.9
B.16
C.25
D.36
9.
2020·武汉模拟
在平面直角坐标系中,圆心为坐标原点,⊙O的半径为10,则P(-10,1)与⊙O的位置关系为( )
A.点P在⊙O上
B.点P在⊙O外
C.点P在⊙O内
D.无法确定
10.
如图,在网格中(每个小正方形的边长均为1个单位长度)选取9个格点(格线的交点称为格点).如果以点A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
图
A.2<r≤
B.<r≤3
C.<r≤5
D.5<r≤
二、填空题(本大题共6道小题)
11.
如图,在平面直角坐标系中,已知C(3,4),以点C为圆心的圆与y轴相切.点A,B在x轴上,且OA=OB.P为⊙C上的动点,∠APB=90°,则AB长的最大值为________.
12.
如图1,已知△ABC的外心为O,BC=10,∠BAC=60°,分别以AB,AC为腰向三角形外作等腰直角三角形ABD与ACE,连接BE,CD交于点P,则OP长的最小值是________.
13.
如图,AB为⊙O的直径,圆周角∠ABC=40°,当∠BCD=________°时,CD为⊙O的切线.
14.
如图,⊙M的圆心在一次函数y=x+2的图象上运动,半径为1.当⊙M与y轴相切时,点M的坐标为__________.
15.
如图所示,在半圆O中,AB是直径,D是半圆O上一点,C是的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,有下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心.其中正确的结论是________(只需填写序号).
16.
如图,半圆的圆心O与坐标原点重合,半圆的半径为1,直线l的解析式为y=x+t.若直线l与半圆只有一个公共点,则t的取值范围是________.
三、解答题(本大题共4道小题)
17.
2018·邵阳
如图所示,AB是⊙O的直径,C为⊙O上一点,过点B作BD⊥CD,垂足为D,连接BC,BC平分∠ABD.
求证:CD为⊙O的切线.
18.
2019·天津
如图,已知PA,PB分别与⊙O相切于点A,B,∠APB=80°,C为⊙O上一点.
(1)如图①,求∠ACB的大小;
(2)如图②,AE为⊙O的直径,AE与BC相交于点D.若AB=AD,求∠EAC的大小.
19.
如图①,直线PA交⊙O于A,E两点,PA的垂线CD切⊙O于点C,交PA于点D,过点A作⊙O的直径AB.
(1)求证:AC平分∠DAB;
(2)如图②,将直线CD向下平行移动,得到CD与⊙O相切于点C,AC还平分∠DAB吗?请说明理由.
解题突破(20题)
在动态情况下,探究结论是否发生变化,主要看使结论成立的主要条件是否改变.比如本题中虽然图形发生变化,但AD和OC平行,△AOC是等腰三角形这两个主要条件没有改变,因此结论不发生变化.
20.
如图,AB是⊙O的直径,AB=8,点C在⊙O的半径OA上运动,PC⊥AB,垂足为C,PC=5,PT为⊙O的切线,切点为T.
(1)如图①,当点C运动到点O时,求PT的长;
(2)如图②,当点C运动到点A时,连接PO,BT,求证:PO∥BT;
(3)如图③,设PT2=y,AC=x,求y与x之间的函数解析式及y的最小值.
人教版
九年级数学上册
24.2
点和圆、直线和圆的位置关系
同步课时训练-答案
一、选择题(本大题共10道小题)
1.
【答案】B
2.
【答案】A [解析]
∵MN是⊙O的切线,∴ON⊥NM,∴∠ONM=90°,
∴∠ONB=90°-∠MNB=90°-52°=38°.
∵ON=OB,∴∠B=∠ONB=38°,∴∠NOA=2∠B=76°.
3.
【答案】D
4.
【答案】C [解析]
因为所求直线到圆心O的距离为2.2
cm>半径2
cm,所以此直线与⊙O相离,所以这条直线为直线l3.
5.
【答案】B [解析]
由题意可知∠BCN=60°,∠ACN=30°,∴∠ACB=∠ACN+∠BCN=90°,
∴△ABC是直角三角形,
∴△ABC的外心是斜边AB的中点.
∵Q是AB的中点,
∴△ABC的外心是点Q.
6.
【答案】C [解析]
如图.
7.
【答案】B [解析]
如图,连接OC,并过点O作OF⊥CE于点F.
∵△ABC为等边三角形,边长为4
cm,
∴△ABC的高为2
cm,∴OC=
cm.
又∵⊙O与BC相切于点C,∠ACB=60°,
∴∠OCF=30°.
在Rt△OFC中,可得FC=
cm,
∴CE=2FC=3
cm.
8.
【答案】B [解析]
如图,连接OC交⊙C于点P′.
∵圆心C的坐标为(3,4),点P的坐标为(m,n),
∴OC=5,OP=,
∴m2+n2是点P到原点的距离的平方,
∴当点P运动到线段OC上,即点P′处时,点P离原点最近,即m2+n2取得最小值,
此时OP=OC-PC=5-1=4,即m2+n2=16.
9.
【答案】B
10.
【答案】B [解析]
如图,∵AD=2
,AE=AF=,AB=3
,
∴AB>AE=AF>AD,
∴当<r<3
时,以点A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内.
二、填空题(本大题共6道小题)
11.
【答案】16
12.
【答案】5- [解析]
∵∠BAD=∠CAE=90°,
∴∠DAC=∠BAE.
在△DAC和△BAE中,
∴△DAC≌△BAE(SAS),
∴∠ADC=∠ABE,
从而∠PDB+∠PBD=90°,
即∠DPB=90°,从而∠BPC=90°,
∴点P在以BC为直径的圆上.
如图,过点O作OH⊥BC于点H,连接OB,OC.
∵△ABC的外心为O,∠BAC=60°,
∴∠BOC=120°.又∵BC=10,
∴OH=
,∴OP长的最小值是5- .
13.
【答案】50 [解析]
连接OC.
∵OC=OB,∴∠OCB=∠ABC=40°.
∵∠BCD=50°,∴∠OCD=90°,
∴CD为⊙O的切线.
14.
【答案】(1,)或(-1,) [解析]
∵⊙M的圆心在一次函数y=x+2的图象上运动,∴设当⊙M与y轴相切时圆心M的坐标为(x,x+2).∵⊙M的半径为1,∴x=1或x=-1,当x=1时,y=,当x=-1时,y=.∴点M的坐标为(1,)或(-1,).
15.
【答案】②③ [解析]
∵在半圆O中,AB是直径,D是半圆O上一点,C是的中点,
∴=,但不一定等于,
∴∠BAD与∠ABC不一定相等,故①错误.
如图,连接OD,则OD⊥GD,∠OAD=∠ODA.
∵∠ODA+∠GDP=90°,∠OAD+∠GPD=∠OAD+∠APE=90°,
∴∠GPD=∠GDP,∴GP=GD,故②正确.
补全⊙O,延长CE交⊙O于点F.
∵CE⊥AB,∴A为的中点,即=.
又∵C为的中点,∴=,∴=,
∴∠CAP=∠ACP,∴AP=CP.
∵AB为⊙O的直径,∴∠ACQ=90°,
∴∠ACP+∠PCQ=90°,∠CAP+∠PQC=90°,
∴∠PCQ=∠PQC,∴PC=PQ,
∴AP=PQ,即P为Rt△ACQ的斜边AQ的中点,
∴点P为Rt△ACQ的外心,故③正确.
16.
【答案】t=或-1≤t<1 [解析]
若直线与半圆只有一个公共点,则有两种情况:直线和半圆相切于点C或从直线过点A开始到直线过点B结束(不包括直线过点A).
直线y=x+t与x轴所形成的锐角是45°.
当点O到直线l的距离OC=1时,直线l与半圆O相切,设直线l与y轴交于点D,则OD=,即t=.
当直线过点A时,把A(-1,0)代入直线l的解析式,得t=y-x=1.
当直线过点B时,把B(1,0)代入直线l的解析式,得t=y-x=-1.
即当t=或-1≤t<1时,直线和半圆只有一个公共点.
故答案为t=或-1≤t<1.
三、解答题(本大题共4道小题)
17.
【答案】
证明:连接OC.∵BC平分∠ABD,
∴∠OBC=∠DBC.
∵OB=OC,∴∠OBC=∠OCB,
∴∠OCB=∠DBC,
∴OC∥BD.
∵BD⊥CD,∴OC⊥CD,∴CD为⊙O的切线.
18.
【答案】
解:(1)如图①,连接OA,OB,
∵PA,PB是⊙O的切线,
∴∠OAP=∠OBP=90°,
∴∠AOB=360°-90°-90°-80°=100°.
由圆周角定理,得∠ACB=∠AOB=50°.
(2)如图②,连接CE.
∵AE为⊙O的直径,
∴∠ACE=90°.
∵∠ACB=50°,
∴∠BCE=90°-50°=40°,
∴∠BAE=∠BCE=40°.
∵AB=AD,
∴∠ABD=∠ADB=70°,
∴∠EAC=∠ADB-∠ACB=20°.
19.
【答案】
解:(1)证明:连接OC.
∵OA=OC,∴∠OAC=∠OCA.
∵CD切⊙O于点C,∴CD⊥OC.
又∵CD⊥PA,∴OC∥PA,∴∠PAC=∠OCA,
∴∠OAC=∠PAC,即AC平分∠DAB.
(2)AC还平分∠DAB.理由:连接OC.
∵CD切⊙O于点C,∴CD⊥OC.
又∵AD⊥CD,∴OC∥AD,
∴∠OCA=∠DAC.
又∵OA=OC,
∴∠OAC=∠OCA,
∴∠DAC=∠OAC,
即AC平分∠DAB.
20.
【答案】
解:(1)连接OT.
∵PT为⊙O的切线,∴OT⊥PT,
∴在Rt△PTO中,PT==3.
(2)证明:连接AT,OT.
∵PT为⊙O的切线,
∴PT⊥OT,
∴∠PTO=90°=∠PAO.
在Rt△PAO和Rt△PTO中,
∵PO=PO,OA=OT,
∴Rt△PAO≌Rt△PTO,
∴PA=PT,∠APO=∠TPO,∴PO⊥AT.
∵AB是⊙O的直径,
∴∠ATB是直角,即BT⊥AT,∴PO∥BT.
(3)连接PO,OT.
∵PT为⊙O的切线,∴PT⊥OT.
∵AC=x,∴CO=OA-AC=4-x.
在Rt△PCO中,PO2=PC2+CO2=52+(4-x)2.
在Rt△POT中,PO2=PT2+OT2=PT2+42,
∴PT2+42=52+(4-x)2,
即y+42=52+(4-x)2,
∴y=9+(4-x)2=x2-8x+25=(x-4)2+9(0≤x≤4),
∴当x=4时,y有最小值9.
∴y与x之间的函数解析式为y=x2-8x+25(0≤x≤4),y的最小值是9.
同课章节目录
