苏科版九年级上册数学 2.4圆周角 教案

版 本：苏教版
年 级：九年级上册
教学设计要求
学校名称 苏州高新区第一初级中学校
课例名称 2.4 圆周角 教师姓名 单净璇
学段学科 数学，初中 教材版本 苏教版
章节 义务教育教科书（苏教版）
九年级上册第二章 年级 九年级
教学目标 知识技能：了解圆周角的概念，探索圆周角与圆心角及其所对弧的关系；了解并证明圆周角定理，能应用圆周角定理解决简单的说理和计算问题。
数学思考：通过对圆周角定理的探索体会分类、化归、由特殊到一般等数学思想，学会从数学的角度思考问题。
问题解决：在探索圆周角与圆心角关系时，培养观察、比较、分析、推理能力，利用圆心在圆周角边上的特殊情形证明另外两种情况，积累基本的数学活动经验，提高运用数学知识解决问题的能力。
情感态度：积极参与数学活动，在探索、交流的过程中增强合作能力，通过解决问题增强自信心，激发学习数学的兴趣。感受数学来源于生活，服务于生活。

教学 重难点 教学重点：探索圆周角与圆心角的关系。
教学难点：通过分类讨论，推理、验证“圆周角与圆心角的关系”。
学情分析 本节课基于前面已经学习了圆的定义、圆的对称性之后对圆周角与圆心角关系进行探索的一节新课。
本班学生基础知识扎实，有良好的学习习惯，课堂参与性强，思维活跃，有基本的数学语言表达能力，具备一定的数学探究活动经验和应用数学的意识。会操作平板电脑和交互式电子白板，具备一定的智慧学习平台的经验。
教学方法 本节课以情境与教学内容双主线并行，以微信任务推动教学。
学生通过观察发现、自主探索、合作交流，探究圆周角和圆心角关系并验证。教师设置情境化的课堂学习任务单，多种信息技术手段辅助（交互式电子白板、几何画板、平板电脑、微课、理想云平台等）启发式设疑引导学生，并最终帮助学生完成对圆周角定义、圆周角定理及其应用知识体系的构建。

教学过程 教学流程图
教学步骤
教师行为
学生行为
教学资源
设计意图
与分析
一
：
创设情境
，
提出问题
创设情境，提出问题
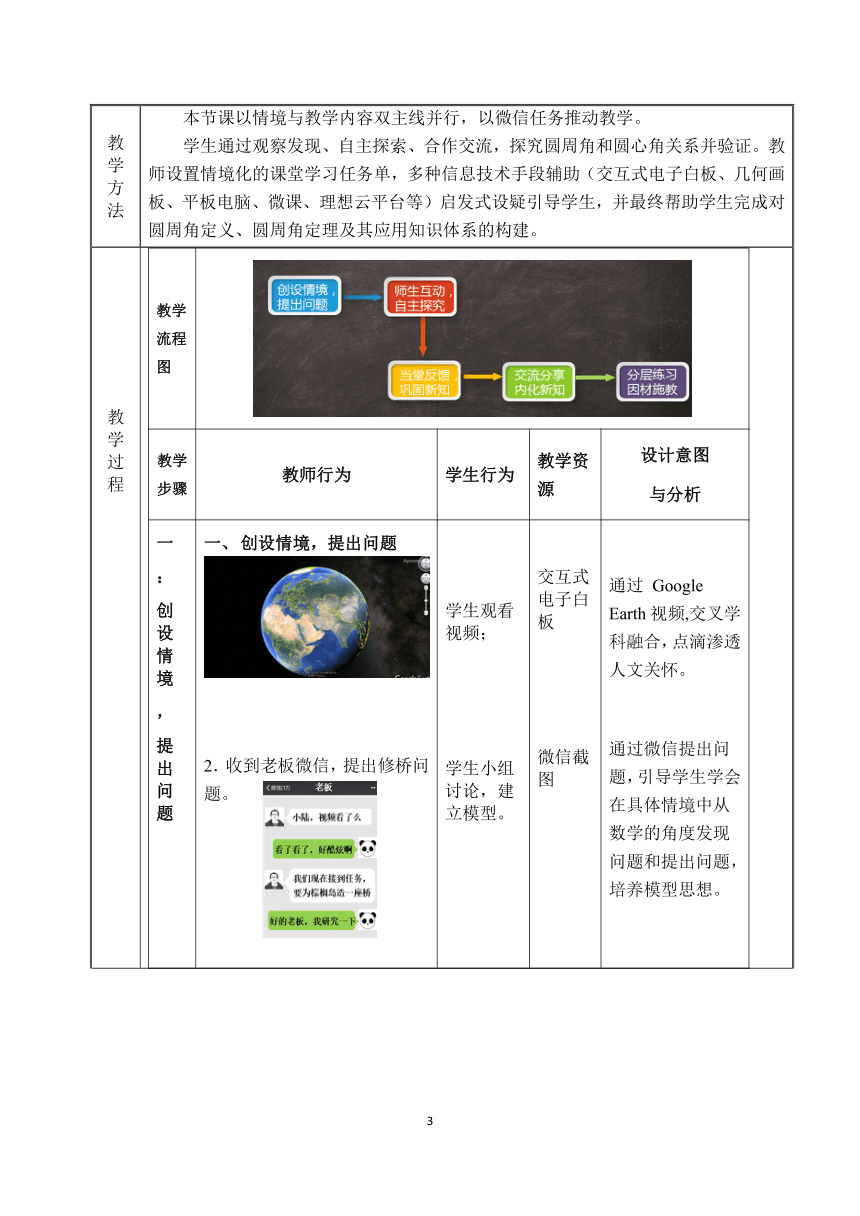
1．Google Earth视频导入，介绍棕榈岛；
2．收到老板微信，提出修桥问题。
学生观看视频；
学生小组讨论，建立模型。
交互式电子白板
微信截图
通过 Google Earth视频,交叉学科融合，点滴渗透人文关怀。
通过微信提出问题，引导学生学会在具体情境中从数学的角度发现问题和提出问题，培养模型思想。
二
：
师生互动
，
自主探究
师生互动,自主探究
1.学生建模，在课堂学习任务单1上画出数学图形。根据提供的三家公司的二维码及对应知识点进行扫描，引导学生一起总结出解决问题的思路，学生写在课堂学习任务单1上，教师写在黑板上。
2.移动小船位置，引导学生总结特征，得出圆周角的定义。
给出一组图形辨别。
3.多种手段、突破难点。引导学生自主探索圆周角与圆心角的关系。
（1）几何画板度量展示：①圆周上点A的移动，②半径大小改变，∠BAC度数不变，猜想同弧所对的圆周角度数不变。
（2）学生在课堂任务学习单2上进行第一项任务：画图度量，填表后小组交流。
（3）几何画板度量弧AC，弧BC，弧AB的度数，展示随着点A的移动，只有弧BC的度数不变，且一直是∠BAC的两倍，猜想圆周角度数是它所对弧上圆心角度数的一半。
（4）随着点A的移动，圆心O与∠BAC的位置关系如何。
（5）引导学生在课堂任务学习单2上进行第二项任务，分三种情形自主探究，演绎推理，并推屏展示。
（5）利用老师之前录好的微课推送给独立证明有困难的同学，观看证明过程。
（6）几何画板展示，利用上述已证圆周角和圆心角的关系证明等弧所对的圆周角相等
（7）引导学生归纳、总结圆周角定理，并板书。
学生画图，建模。
学生扫描二维码，小组交流，分析方案。
学生通过观察，类比圆心角的概念讨论圆周角的定义。
学生观看演示，小组讨论，得出猜想1
学生画出同弧所对的圆周角和圆心角，并用量角器量出度数，填写在表格内。
学生观看演示，小组讨论，得出猜想2
学生一遍观看几何画板的运动，一边组内分工，分三种情形画出图形，随后写出证明过程，拍照上传，并自己演示讲解。
部分基础较好的同学独立证明；对部分独立证明有困难的同学，老师推送微课让他们一边观看，一边补充完整自己的证明过程。
学生记录在课堂笔记本上。
平板电脑
自制二维码
交互式电子白板展示
几何画板
交互式电子白板
几何画板
交互式电子白板
Star C平台实现大小屏互动功能
交互式电子白板书写功能
录屏软件Camtasia
Studio
百度网盘
平板电脑
交互式电子白板
将传统的复习旧知以二维码扫描的方式在提出问题后融入课堂，让学生决定复习时间、复习内容，自主寻求学习支架，从已有知识体系中提取有用信息，寻找与新知之间的联系。
通过观察，引导学生发现顶点在圆周上的角与其他不同，类比圆心角的概念给出圆周角的定义。
概念的辨析环节是教学中不可缺少的一部分，并指出它所对的弧为下面做铺垫。
通过几何画板具体数值的展示，形象直观，引导学生不完全归纳，演绎推理，大胆猜想，从特殊到一般。
让学生自己动手操作，体验数据收集、分析过程，同时积累数学活动经验，掌握技能， 提高实践能力。
通过几何画板具体数值的展示，形象直观，引导学生不完全归纳，大胆猜想，体会合情推理探索数学结论。
得到猜想后，进入严谨的证明，这是本节课的一个难点。本环节充分发挥了学生在课堂中的主体性，教师从旁引导和辅助，鼓励学生动手操作，演示讲解，在三种情形的证明中，后两种都转化为第一种情形，渗透分类讨论，从一般到特殊的数学思想。学生自己演示讲解不仅锻炼了运用数学表述的能力，更是从学生的角度，以生教生的方式让学生理解知识，体会运用演绎推理加以证明的过程。
关注学生个体差异，利用微课分层教学，百度网盘分享给部分同学，让独立证明有困难的同学在平板电脑上观看，直观高效，证明过程中渗透分类、化归的数学思想，形成严谨求实的科学态度。
在应用现代信息技术的同时，注重课堂教学的板书设计，让学生一起回顾圆周角与圆心角关系的证明过程，帮助学生梳理思路，必要的板书有利于实现学生思维与教学过程同步，有助于学生更好地把握教学内容的脉络。
环节三
：
当堂反馈
，
巩固新知
三、当堂反馈，巩固新知
1.通过上述分析，引导学生解决修桥问题
2.回到任务开始的三种情形
3.推送当堂反馈练习题
学生解决修桥问题
学生在平板电脑上完成习题，提交
课堂学习任务单
Star C平台、平板电脑
当堂反馈1，既运用新知，又呼应内容主线，解决修桥问题既让学生体会到了解决问题的快乐，增强应用意识。
反馈2，呼应本节课起始情境的三种情况，鼓励学生应用新知解决问题。
反馈3，巩固新知，通过大数据，直观了解学生做题错误率较高的题，从而及时、精准得进行讲评，加深学生对新知的理解。
环节四
：
交流分享
，
内化新知
四、交流分享，内化新知
1.小组讨论，弹幕形式进行本节课小结
学生小组讨论，互相补充、交流
平板电脑
交互式电子白板
引导学生学会反思，完成自己知识体系的构建，促进知识的理解，为后续学习做好铺垫。同时让学生在每个环节都积极参与数学活动，敢于发表自己的想法，在与他人合作交流过程中，理解他人的思考方法和结论。
环节五
：
分层练习
，
因材施教
五、分层练习，因材施教
学生完成作业，提交
理想人人通学生端，教师端
尊重学生个体差异，分层布置作业，满足不同层次的学生的学习需求，让作业成为课堂的延伸，也成为学生能力提升的机会，希望不同的人在数学上得到不同的发展。
板书设计

信息技术融合点
1.利用Google Earth创设情境，渗透人文关怀，提出问题；
2.利用二维码技术，让学生自主复习旧知，调取有用信息并运用解决新问题；
3.利用微信任务推动课堂教学；
4.利用几何画板动态演示，形象直观，帮助学生大胆猜想，突破难点；
5.利用情境化的2份课堂学习任务单，双主线贯穿探索活动；
6.利用StarC的课堂互动功能让学生完成数据共享，演示讲解；当堂反馈中利用StarC的随堂小考功能，从大数据上了解学生做题情况，精准点评，打造高效课堂；
7.利用交互式电子白板，多次使用书写功能，让师生的思维过程显性化；
8.在师生多种手段共同探究圆周角与圆心角关系后，老师利用录屏软件Camtasia
Studio录制微课帮助独立证明有困难的学生梳理思路，严谨演绎推理，从而形成老师、学生、视频多种讲解形式；
9.利用理想人人通的教师端分层布置作业，学生端完成后，老师批改后，对有问题的同学及时点拨，帮助学生更好把握新知。
教学反思 这一节课的教学实施，感觉到自己在以下几个方面做得有新意：
情境引入新颖，激发了学生对本节课的学习兴趣；
鼓励学生在具体情境中从数学的角度发现问题和提出问题，培养模型思想；
利用微信任务推动教学，以AutoCAD图纸为载体设置相应的课堂学习任务单，以二维码技术支持复习旧知，学生全程浸入式学习；
利用StarC大小屏适时互动，师生交互更加及时高效；
在突破圆周角与圆心角关系的难点时，分学生量角器操作、记录、交流，教师几何画板展示猜想，学生课堂任务单中证明，老师微课梳理四步逐步深入，螺旋上升，渗透分类、化归、从特殊到一般的数学思想，达到了较好的效果；
采用小组合作教学模式，鼓励学生自己推屏讲演，从而培养学生独立思考、合作学习的能力，增强应用意识，提高实践能力。
不足之处：在量取圆周角、圆心角度数进行填表时，没有把全班数据集成，仅是小组共享，数据量有些小。
9