23.4 中位线 课件(共23张PPT)
文档属性
| 名称 | 23.4 中位线 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 799.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-29 05:56:10 | ||
图片预览



文档简介
(共23张PPT)
23.4
中位线
华东师大版
九年级数学上册
学习目标:
1.
经历三角形中位线的性质定理形成过程.
2.
掌握三角形中位线的性质定理,并能利用它解决简单的问题.
3.
通过命题的教学了解常用的辅助线的作法,并能灵活运用它们解题,进一步训练说理的能力.
学习重点:
三角形中位线的性质定理.
学习难点:
三角形中位线的性质定理的应用.
在
23.3
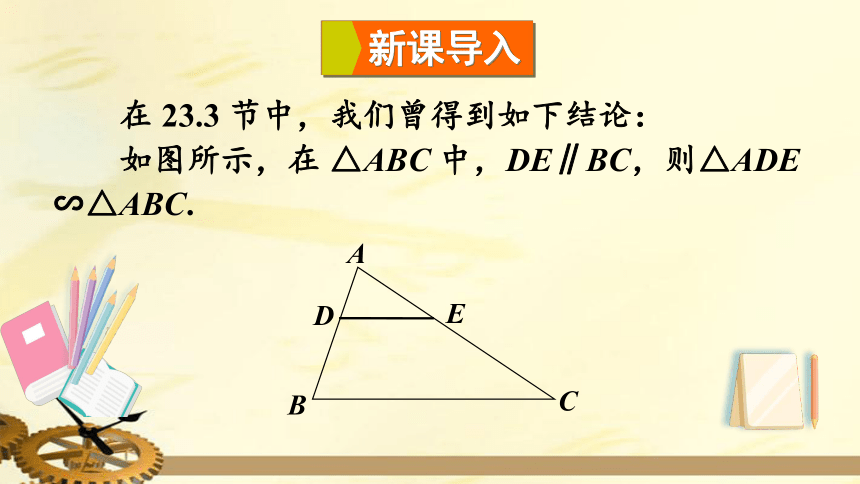
节中,我们曾得到如下结论:
如图所示,在
△ABC
中,DE∥BC,则△ADE
∽△ABC.
新课导入
A
B
C
E
D
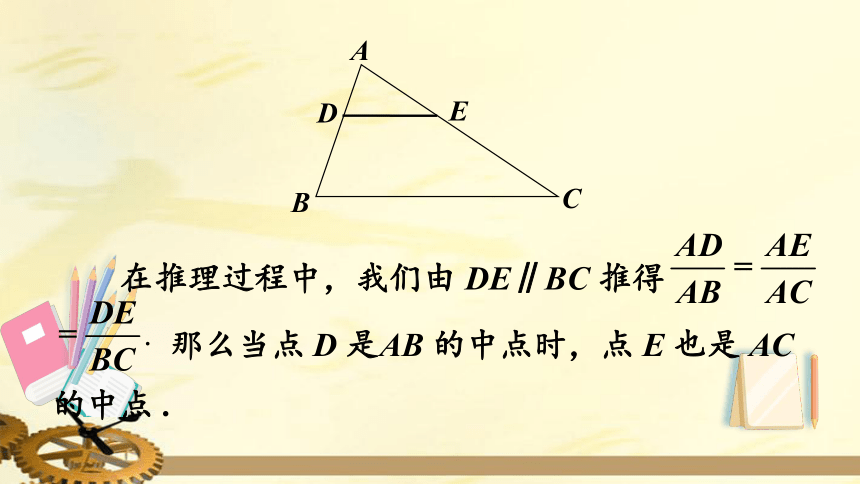
在推理过程中,我们由
DE∥BC
推得
那么当点
D
是AB
的中点时,点
E
也是
AC
的中点
.
A
B
C
E
D
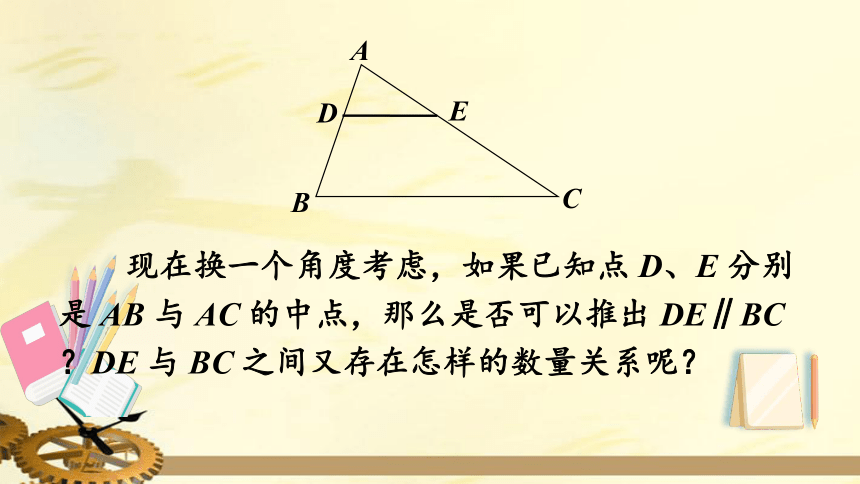
现在换一个角度考虑,如果已知点
D、E
分别
是
AB
与
AC
的中点,那么是否可以推出
DE∥BC?DE
与
BC
之间又存在怎样的数量关系呢?
A
B
C
E
D
推进新课
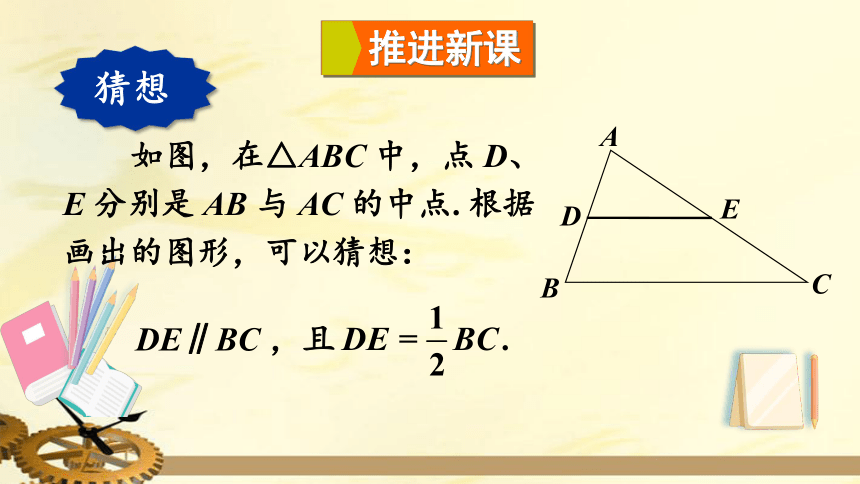
如图,在△ABC
中,点
D、E
分别是
AB
与
AC
的中点.
根据画出的图形,可以猜想:
猜想
A
B
C
E
D
DE∥BC
,且
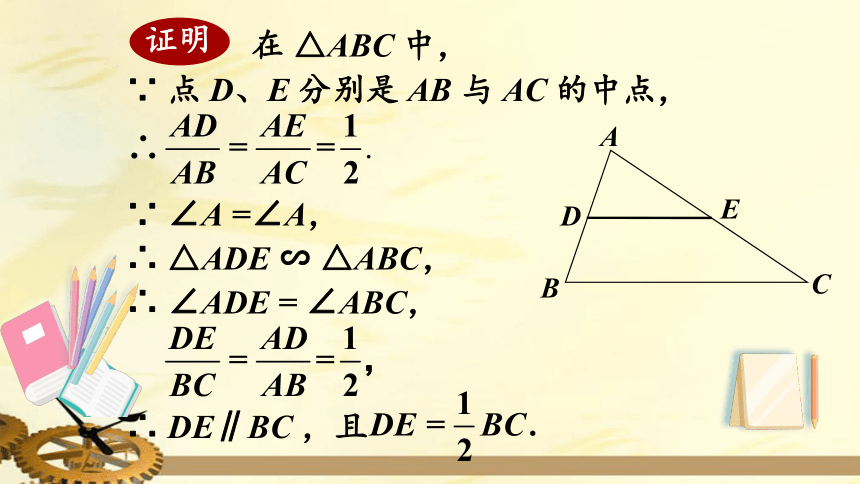
在
△ABC
中,
∵
点
D、E
分别是
AB
与
AC
的中点,
∵
∠A
=∠A,
∴
△ADE
∽
△ABC,
∴
∠ADE
=
∠ABC,
∴
DE∥BC
,且
证明
A
B
C
E
D
A
B
C
E
D
F
A
B
C
E
D
M
N
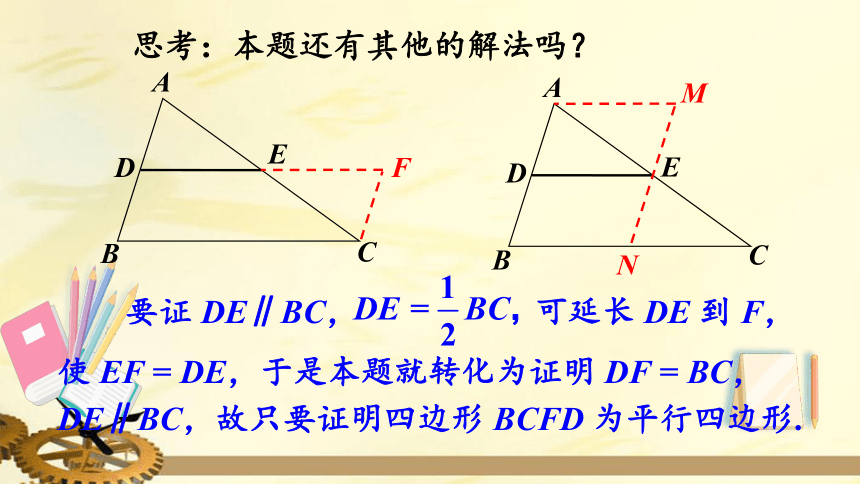
要证
DE∥BC,
可延长
DE
到
F,
使
EF
=
DE,于是本题就转化为证明
DF
=
BC,
DE∥BC,故只要证明四边形
BCFD
为平行四边形.
思考:本题还有其他的解法吗?
我们把连结三角形两边中点的线段叫做三角形的中位线,并且有:
三角形的中位线平行于第三边,并且等于第三边的一半.
概括
求证:三角形的一条中位线与第三边上的中线互相平分.
已知:如图,在
△ABC
中,AD
=
DB,BE
=
EC,AF
=
FC
.
求证:AE、DF
互相平分.
例1
证明
连结
DE、EF.
∵
AD
=
DB,BE
=
EC,
∴
DE∥AC(三角形的中位线平行于第三边,并且等于第三边的一半).
同理可得
EF∥BA
.
∴
四边形
ADEF
是平行四边形.
∴
AE、DF
互相平分.
如图,在△ABC
中,D、E
分别是边BC、AB
的中点,AD、CE
相交于点
G
.
求证:
例2
证明
连结
ED.
∵
D、E
分别是边
BC、AB
的中点,
∴
DE∥AC
,
(三角形的中位线平行于第三边,
并且等于第三边的一半),
∴
△ACG
∽
△DEG
,
拓展
如果在例2的图中取
AC
的中点
F,假设
BF
与
AD
相交于点
G′,如图,那么我们同理可得
即两图中的
G
与
G′
是重合的,
由此我们可以得出什么结论?
于是,我们有以下结论:
三角形三条边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的连线的长是对应中线长的
.
随堂演练
1.如图,在□ABCD中,有
E、F
分别是AD、BC上的点,且DE
=
CF,BE
和
AF
的交点为
M,CE
和
DF
的交点为
N.
求证:MN∥AD,
解:连结
EF,证四边形
ABFE
和四边形
DCFE
均为平行四边形,得
FM
=
AM,FN
=
DN.
∴MN∥AD,
2.
如图,在四边形ABCD
中,对角线
AC、BD交于点
O,E、F
分别是
AB、CD
的中点,且
AC
=
BD.
求证:OM
=
ON.
解:取BC的中点G,连接EG、FG,
∵
BG
=
CG,BE
=
AE,
EG∥AC
∴
∠ONM
=
∠GEF,
同理
∠OMN
=
∠GFE,
∵
AC
=
BD,∴
GE
=
GF,
∴∠GEF
=∠GFE,
∴∠ONM
=∠OMN,
∴
OM
=
ON.
课堂小结
1.三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
2.三角形中位线定理的应用.
3.三角形重心的性质.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本课时从学过的知识入手猜想中位线的性质,并通过动手画图、操作,证明猜想,体会知识的形成过程,加深对知识的理解.在证明的过程中举一反三,用多种方法证明三角形中位线定理,通过具体的实例分析,提高学生应用知识的能力.
谢谢欣赏
23.4
中位线
华东师大版
九年级数学上册
学习目标:
1.
经历三角形中位线的性质定理形成过程.
2.
掌握三角形中位线的性质定理,并能利用它解决简单的问题.
3.
通过命题的教学了解常用的辅助线的作法,并能灵活运用它们解题,进一步训练说理的能力.
学习重点:
三角形中位线的性质定理.
学习难点:
三角形中位线的性质定理的应用.
在
23.3
节中,我们曾得到如下结论:
如图所示,在
△ABC
中,DE∥BC,则△ADE
∽△ABC.
新课导入
A
B
C
E
D
在推理过程中,我们由
DE∥BC
推得
那么当点
D
是AB
的中点时,点
E
也是
AC
的中点
.
A
B
C
E
D
现在换一个角度考虑,如果已知点
D、E
分别
是
AB
与
AC
的中点,那么是否可以推出
DE∥BC?DE
与
BC
之间又存在怎样的数量关系呢?
A
B
C
E
D
推进新课
如图,在△ABC
中,点
D、E
分别是
AB
与
AC
的中点.
根据画出的图形,可以猜想:
猜想
A
B
C
E
D
DE∥BC
,且
在
△ABC
中,
∵
点
D、E
分别是
AB
与
AC
的中点,
∵
∠A
=∠A,
∴
△ADE
∽
△ABC,
∴
∠ADE
=
∠ABC,
∴
DE∥BC
,且
证明
A
B
C
E
D
A
B
C
E
D
F
A
B
C
E
D
M
N
要证
DE∥BC,
可延长
DE
到
F,
使
EF
=
DE,于是本题就转化为证明
DF
=
BC,
DE∥BC,故只要证明四边形
BCFD
为平行四边形.
思考:本题还有其他的解法吗?
我们把连结三角形两边中点的线段叫做三角形的中位线,并且有:
三角形的中位线平行于第三边,并且等于第三边的一半.
概括
求证:三角形的一条中位线与第三边上的中线互相平分.
已知:如图,在
△ABC
中,AD
=
DB,BE
=
EC,AF
=
FC
.
求证:AE、DF
互相平分.
例1
证明
连结
DE、EF.
∵
AD
=
DB,BE
=
EC,
∴
DE∥AC(三角形的中位线平行于第三边,并且等于第三边的一半).
同理可得
EF∥BA
.
∴
四边形
ADEF
是平行四边形.
∴
AE、DF
互相平分.
如图,在△ABC
中,D、E
分别是边BC、AB
的中点,AD、CE
相交于点
G
.
求证:
例2
证明
连结
ED.
∵
D、E
分别是边
BC、AB
的中点,
∴
DE∥AC
,
(三角形的中位线平行于第三边,
并且等于第三边的一半),
∴
△ACG
∽
△DEG
,
拓展
如果在例2的图中取
AC
的中点
F,假设
BF
与
AD
相交于点
G′,如图,那么我们同理可得
即两图中的
G
与
G′
是重合的,
由此我们可以得出什么结论?
于是,我们有以下结论:
三角形三条边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的连线的长是对应中线长的
.
随堂演练
1.如图,在□ABCD中,有
E、F
分别是AD、BC上的点,且DE
=
CF,BE
和
AF
的交点为
M,CE
和
DF
的交点为
N.
求证:MN∥AD,
解:连结
EF,证四边形
ABFE
和四边形
DCFE
均为平行四边形,得
FM
=
AM,FN
=
DN.
∴MN∥AD,
2.
如图,在四边形ABCD
中,对角线
AC、BD交于点
O,E、F
分别是
AB、CD
的中点,且
AC
=
BD.
求证:OM
=
ON.
解:取BC的中点G,连接EG、FG,
∵
BG
=
CG,BE
=
AE,
EG∥AC
∴
∠ONM
=
∠GEF,
同理
∠OMN
=
∠GFE,
∵
AC
=
BD,∴
GE
=
GF,
∴∠GEF
=∠GFE,
∴∠ONM
=∠OMN,
∴
OM
=
ON.
课堂小结
1.三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
2.三角形中位线定理的应用.
3.三角形重心的性质.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本课时从学过的知识入手猜想中位线的性质,并通过动手画图、操作,证明猜想,体会知识的形成过程,加深对知识的理解.在证明的过程中举一反三,用多种方法证明三角形中位线定理,通过具体的实例分析,提高学生应用知识的能力.
谢谢欣赏
