23.1图形的旋转

(共27张PPT)
目标引领
1.通过观察具体实例认识旋转，
理解旋转的基本涵义；
2.探索旋转的基本性质;
⒊利用旋转的性质解决数学问题。
下面情景中的转动现象，有什么共同的特征？
世界如此美丽
踢踢你的腿
转转你的脖子
扭扭你的腰
绕绕你的胳膊
把一个平面图形绕着平面内某一点O转动一个角度，就叫做图形的旋转．这个定点O叫旋转中心，转动的角叫做旋转角．
如果图形上的点P经过旋转变为点P′，那么这两个点P和P′叫做这个旋转的对应点.
动态演示
O
P′
P
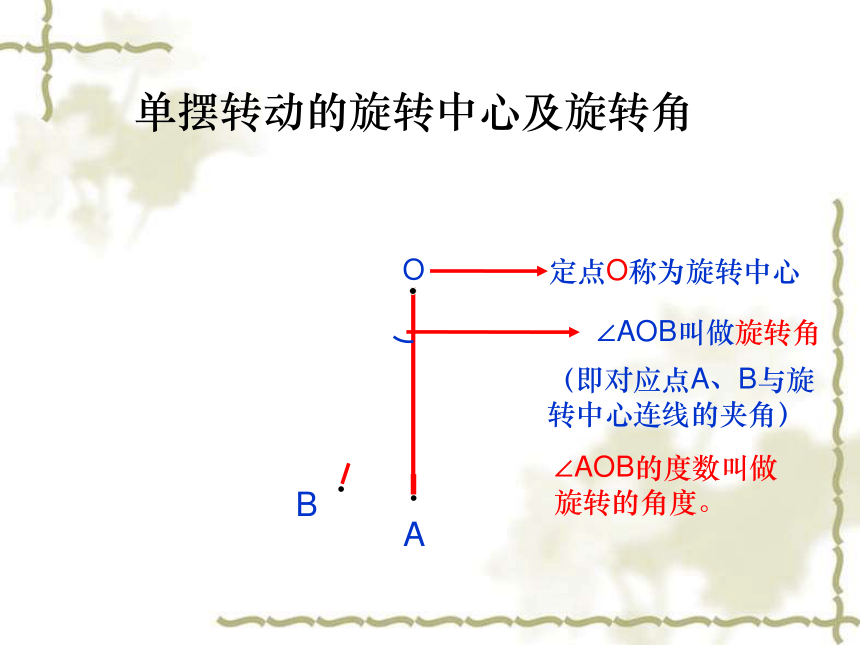
单摆转动的旋转中心及旋转角
O
∠AOB叫做旋转角
定点O称为旋转中心
（即对应点A、B与旋 转中心连线的夹角）
∠AOB的度数叫做旋转的角度。
A
·
·
B
把一个平面图形绕着平面内某一点O转动一个角度，就叫做图形的旋转．这个定点O叫旋转中心，转动的角叫做旋转角．
如果图形上的点P经过旋转变为点P′，那么这两个点P和P′叫做这个旋转的对应点.
动态演示
O
P′
P
例１钟表的分针匀速旋转一周需要60分．
（１）指出它的旋转中心；
（２）经过20分，分针旋转了多少度？
（２）分针匀速旋转一周需要60
　　　分，因此旋转20分，分针
　　　旋转的角度为
解：
（１）它的旋转中心是钟表的轴心
1.下列现象中属于旋转的有( )个.
①地下水位逐年下降；②传送带的移动；③方向盘的转动；
④水龙头的转动； ⑤钟摆的运动； ⑥荡秋千.
A.2 B.3 C.4 D.5
2.举出一些生活中旋转的实例.
3.时钟的时针在不停地转动，从上午6时到上午9时，时针旋转 的旋转角是多少度？从上午9时到上午10时呢？
4.如图，杠杆绕支点转动撬起重物，杠杆的旋转中心在哪里？旋 转角是哪个角？
A
C
B
A
C
B
探 究
在硬纸板上，挖一个三角形洞，再挖一个小洞O作为旋转中心，硬纸板下面放一张白纸．先在纸上描出这个挖掉的三角形洞（△ABC），然后围绕O转动硬纸板，再描出这个挖掉的三角形洞（△A′B′C′），移开硬纸板．
O
A
C
B
C′
B′
A′
请大家运用刻度尺和量角器度量课本上
此图中对应点与旋转中心所连的线段和旋转角，探索旋转的性质．
动态演示
A
C
B
A
C
B
O
A
C
B
C′
B′
A′
动态演示
相等
相等
全等
线段OA与OA′有什么关系？
对应点到旋转中心的距离相等.
∠AOA′与∠ BOB′有什么关系？
对应点与旋转中心所连线段的夹角
都是旋转角.旋转角都相等。
△ABC 与△ A′B′C′有什么关系？
旋转不改变图形的形状和大小，只改变
图形的位置。(旋转前、后的图形全等.)
◆旋转不改变图形的形状和大小，只改变
图形的位置。
(旋转前、后的图形全等.)
◆对应点到旋转中心的距离相等.
◆对应点与旋转中心所连线段的夹
角都是旋转角.旋转角都相等。
旋转的基本性质:
3
44°
5
新知应用
例 : 如图，E是正方形ABCD中CD边上任意一点，以点A为中心，把△ADE顺时针旋转90°，画出旋转后的图形.
分析：关键是确定△ADE三个顶点的对应点，即它们旋转后的位置.
例题尝解
设点E的对应点为点E′，因为旋转后
的图形与旋转前的图形全等，所以
∠ABE′=∠ADE=90°， BE′=DE .
解： 因为点A是旋转中心，所以它的
对应点是它本身.
在正方形ABCD中，AD=AB,
∠DAB=90°，所以旋转后点D与点B重合.
因此，在CB的延长线上取点E′ ，使BE′ =DE，
则△ABE′为旋转后的图形.
例题解答
动态演示
1.如图，小明坐在秋千上，秋千旋转了80°．请在图中小明身上任意选一点P，利用旋转性质，标出点P的对应点．
随堂练习
P●
P’●
2.如图，用左面的三角形经过怎样旋转，可以得到右面的图形．
3.找出图中扳手拧螺母时的旋转中心和旋转角．
答：三角形绕着点O旋转1200，连续旋转两次，可以得到右边的图形
O●
A
A’
O
答：螺母的中心O就是旋转中心，
∠AOA’是旋转角
巩固练习
如图，P是等边 ABC内的一点，把 ABP按不同的方向
通过旋转得到 CBQ和 ACR，
（1）指出旋转中心、旋转方向和旋转角度？
（2） ACR是否能直接绕本身的三个顶点
旋转得到 BCQ ？
A
Q
R
P
C
B
本节课我们主要学了什么内容？
旋转的概念：把一个平面图形绕着平面内某一点0转动一个
角度，就叫做图形的旋转。
决定旋转的三个要素
旋转中心
旋转方向
旋转角度
旋转的性质：
3、旋转不改变图形的大小和形状，只改变图形的位置．
即旋转前后的图形全等。
2、任意一对对应点与旋转中心所连线段的夹角都是旋转角，
旋转角都相等．
1、对应点到旋转中心的距离相等
能力突破
对比平移、轴对称两种图形变换,
旋转变换与它们有哪些共性和区别
再 见！