3.3 勾股定理的应用举例同步练习(含答案)
文档属性
| 名称 | 3.3 勾股定理的应用举例同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-28 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第三章 勾股定理
3 勾股定理的应用举例
夯实基础
知识点一 确定几何体上的最短路线
1.如图,长方体的底面边长分别为1 cm和3 cm,高为6 cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要____________ cm。
第1题图 第2题图
2.如图是一个边长为6的正方体木箱,点Q在上底面的棱上,AQ=2,一只蚂蚁从点P出发沿木箱表面爬行到点Q,则蚂蚁爬行的最短路程是_____________。
3.有一圆柱形油罐,底面圆的周长为24 m,高为5 m,一只老鼠从圆柱形油罐的底端A处爬行到对角B处吃食物,求它爬行的最短路线长。
知识点二 利用勾股定理解决实际问题
4.(长沙中考)我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里、12里、13里,问这块沙田面积有多大?题中的“里”是我国市制长度单位,1里=500m,则该沙田的面积为( )
A. 7.5 km2 B. 15 km2 C. 75 km2 D. 750 km2
5.小明准备测量一段河水的深度,他把一根竹竿竖直插到离岸边1.5 m远的水底,竹竿高出水面0.5 m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )
2 m B. 2.5 m C. 2.25 m D. 3 m
易错点 将长方体展开时,忽视其展开方式不唯一
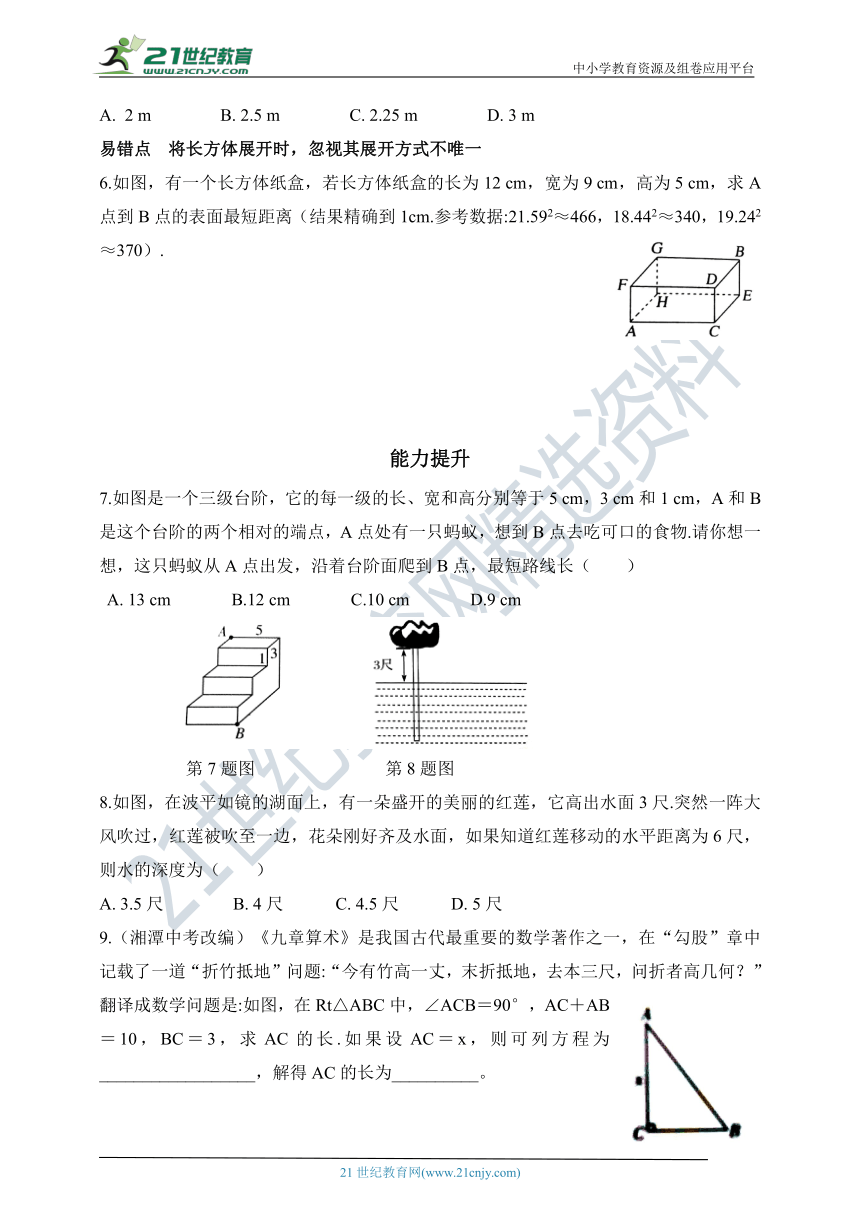
6.如图,有一个长方体纸盒,若长方体纸盒的长为12 cm,宽为9 cm,高为5 cm,求A点到B点的表面最短距离(结果精确到1cm.参考数据:21.592≈466,18.442≈340,19.242≈370).
能力提升
7.如图是一个三级台阶,它的每一级的长、宽和高分别等于5 cm,3 cm和1 cm,A和B是这个台阶的两个相对的端点,A点处有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短路线长( )
A. 13 cm B.12 cm C.10 cm D.9 cm
第7题图 第8题图
8.如图,在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面3尺.突然一阵大风吹过,红莲被吹至一边,花朵刚好齐及水面,如果知道红莲移动的水平距离为6尺,则水的深度为( )
A. 3.5尺 B. 4尺 C. 4.5尺 D. 5尺
9.(湘潭中考改编)《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图,在Rt△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长.如果设AC=x,则可列方程为__________________,解得AC的长为__________。
10.如图,圆柱的底面周长为6 cm,AC为底面圆的直径,高BC=6 cm,点P是BC上一点,且PC=BC一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P,其最短距离为__________。
11.如图,某人到岛上去探宝,从A处登陆后先往东走4 km,又往北走3.5 km,遇到障碍后又往西走1 km,再转向北走到4.5 km处往东一拐,仅走3 km就找到宝藏,问登陆点A与宝藏埋藏点B之间的距离是多少?
12.《中华人民共和国道路交通管理条例》规定:汽车在城市街路上的行驶速度不得超过70 km/h.如图,一辆汽车在一条城市街道上直线行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30 m的C处,过了2 s后,测得汽车与车速检测仪的距离为50 m,这辆汽车超速了吗?(参考数据转换:1m/s=3.6 km/h)
13.如图,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16 n mile,“海天”号每小时航行1 2 n mile,它们离开港口一个半小时后分别位于点Q,R处,且相距30 n mile。
(1)求PQ,PR的距离
(2)如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?圆
素养提升
14.如图,我国海监船在钓鱼岛海域的O点巡航,OA⊥OB,OA=36海里,OB=12海里,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O处,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船。
(1)请用直尺和圆规作出C处的位置;(不写作法,保留作图痕迹)
(2)求我国海监船行驶的航程BC的长。
参考答案
10 2. 10
3.解:根据题意,得AC=5 cm,BC=24×=12 cm。
在Rt△ABC中,AB2=AC2+BC2=52+122=169。所以AB=13 cm。
所以它爬行的最短路线长为13 cm。
A 5. A
6.解:因为12是最长边,所以将长方形ACDF与长方形FDBG展开在同一平面上.
如图,连接AB,则AB2=AC2+BC2=122+(5+9)2=340.
所以AB≈18cm.即点A到点B的表面的最短距离约是18cm.
A 8. C
9. 10. 5 cm
11.解:如图,过点B作BC⊥AC于点C,
则AC=4-1+3=6(km),BC=4.5+3.5=8(km)
在Rt△ABC中,由勾股定理,得AB2=AC2+BC2=62+82=102.
所以AB=10 km.
所以登陆点A与宝藏埋藏点B之间的距离是10 km。
12.解:在Rt△ABC中,AC=30 m,AB=50 m,
根据勾股定理,得BC===40(m),
所以小汽车的速度为=20(m/s)=72(km/h)。
因为72 km/h>70 km/h,所以这辆小汽车超速行驶。
13.解:(1)PQ=16×1.5=24(n mile),PR=12×1.5=18(n mile)
(2)因为PR2+PQ2=182+242=302=RQ2,所以∠RPQ=90°。
因为“远航”号沿东北方向航行,所以“海天号沿西北方向(或北偏西45°)航行。
14.解:(1)如图,作AB的垂直平分线与OA交于点C。
(2)连接BC,由作图可得:CD为AB的垂直平分线,则CB=CA。
由题意可得:OC=36-CA=36-CB。
因为OA⊥OB,所以在Rt△BOC中,BO2+OC2=BC2,即122+(36-BC)2=BC2,
解得BC=20海里。
所以我国海监船行驶的航程BC的长为20海里。
_21?????????è?????(www.21cnjy.com)_
第三章 勾股定理
3 勾股定理的应用举例
夯实基础
知识点一 确定几何体上的最短路线
1.如图,长方体的底面边长分别为1 cm和3 cm,高为6 cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要____________ cm。
第1题图 第2题图
2.如图是一个边长为6的正方体木箱,点Q在上底面的棱上,AQ=2,一只蚂蚁从点P出发沿木箱表面爬行到点Q,则蚂蚁爬行的最短路程是_____________。
3.有一圆柱形油罐,底面圆的周长为24 m,高为5 m,一只老鼠从圆柱形油罐的底端A处爬行到对角B处吃食物,求它爬行的最短路线长。
知识点二 利用勾股定理解决实际问题
4.(长沙中考)我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里、12里、13里,问这块沙田面积有多大?题中的“里”是我国市制长度单位,1里=500m,则该沙田的面积为( )
A. 7.5 km2 B. 15 km2 C. 75 km2 D. 750 km2
5.小明准备测量一段河水的深度,他把一根竹竿竖直插到离岸边1.5 m远的水底,竹竿高出水面0.5 m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )
2 m B. 2.5 m C. 2.25 m D. 3 m
易错点 将长方体展开时,忽视其展开方式不唯一
6.如图,有一个长方体纸盒,若长方体纸盒的长为12 cm,宽为9 cm,高为5 cm,求A点到B点的表面最短距离(结果精确到1cm.参考数据:21.592≈466,18.442≈340,19.242≈370).
能力提升
7.如图是一个三级台阶,它的每一级的长、宽和高分别等于5 cm,3 cm和1 cm,A和B是这个台阶的两个相对的端点,A点处有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短路线长( )
A. 13 cm B.12 cm C.10 cm D.9 cm
第7题图 第8题图
8.如图,在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面3尺.突然一阵大风吹过,红莲被吹至一边,花朵刚好齐及水面,如果知道红莲移动的水平距离为6尺,则水的深度为( )
A. 3.5尺 B. 4尺 C. 4.5尺 D. 5尺
9.(湘潭中考改编)《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图,在Rt△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长.如果设AC=x,则可列方程为__________________,解得AC的长为__________。
10.如图,圆柱的底面周长为6 cm,AC为底面圆的直径,高BC=6 cm,点P是BC上一点,且PC=BC一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P,其最短距离为__________。
11.如图,某人到岛上去探宝,从A处登陆后先往东走4 km,又往北走3.5 km,遇到障碍后又往西走1 km,再转向北走到4.5 km处往东一拐,仅走3 km就找到宝藏,问登陆点A与宝藏埋藏点B之间的距离是多少?
12.《中华人民共和国道路交通管理条例》规定:汽车在城市街路上的行驶速度不得超过70 km/h.如图,一辆汽车在一条城市街道上直线行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30 m的C处,过了2 s后,测得汽车与车速检测仪的距离为50 m,这辆汽车超速了吗?(参考数据转换:1m/s=3.6 km/h)
13.如图,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16 n mile,“海天”号每小时航行1 2 n mile,它们离开港口一个半小时后分别位于点Q,R处,且相距30 n mile。
(1)求PQ,PR的距离
(2)如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?圆
素养提升
14.如图,我国海监船在钓鱼岛海域的O点巡航,OA⊥OB,OA=36海里,OB=12海里,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O处,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船。
(1)请用直尺和圆规作出C处的位置;(不写作法,保留作图痕迹)
(2)求我国海监船行驶的航程BC的长。
参考答案
10 2. 10
3.解:根据题意,得AC=5 cm,BC=24×=12 cm。
在Rt△ABC中,AB2=AC2+BC2=52+122=169。所以AB=13 cm。
所以它爬行的最短路线长为13 cm。
A 5. A
6.解:因为12是最长边,所以将长方形ACDF与长方形FDBG展开在同一平面上.
如图,连接AB,则AB2=AC2+BC2=122+(5+9)2=340.
所以AB≈18cm.即点A到点B的表面的最短距离约是18cm.
A 8. C
9. 10. 5 cm
11.解:如图,过点B作BC⊥AC于点C,
则AC=4-1+3=6(km),BC=4.5+3.5=8(km)
在Rt△ABC中,由勾股定理,得AB2=AC2+BC2=62+82=102.
所以AB=10 km.
所以登陆点A与宝藏埋藏点B之间的距离是10 km。
12.解:在Rt△ABC中,AC=30 m,AB=50 m,
根据勾股定理,得BC===40(m),
所以小汽车的速度为=20(m/s)=72(km/h)。
因为72 km/h>70 km/h,所以这辆小汽车超速行驶。
13.解:(1)PQ=16×1.5=24(n mile),PR=12×1.5=18(n mile)
(2)因为PR2+PQ2=182+242=302=RQ2,所以∠RPQ=90°。
因为“远航”号沿东北方向航行,所以“海天号沿西北方向(或北偏西45°)航行。
14.解:(1)如图,作AB的垂直平分线与OA交于点C。
(2)连接BC,由作图可得:CD为AB的垂直平分线,则CB=CA。
由题意可得:OC=36-CA=36-CB。
因为OA⊥OB,所以在Rt△BOC中,BO2+OC2=BC2,即122+(36-BC)2=BC2,
解得BC=20海里。
所以我国海监船行驶的航程BC的长为20海里。
_21?????????è?????(www.21cnjy.com)_
