第三章 勾股定理章末复习题(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
第三章 勾股定理
章末复习
[考点突破]
考点1 勾股定理及其验证
1.(淄博校级期中联考)如图,在Rt△ABC中,∠C=90°,D为AC上一点,且DA=DB=5.如果△DAB的面积为10,那么DC的长是( )
A. 3 B. 4 C. 5 D. 6
第1题图 第2题图
2.如图是一张直角三角形的纸片,两直角边分别为AC=6 cm,BC=8 cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
A. 4 cm B. 5 cm C. 6 cm D. 10 cm
考点2 直角三角形的判定
3.(南通中考)下列长度的三条线段能组成直角三角形的是( )
A. 3,4,5 B. 2,3,4 C. 4,6,7 D. 5,11,12
4.(泰安新泰市月考)在△ABC中,AB=12 cm,AC=9 cm,BC=15 cm,则S△ABC为( )
A. 54cm2 B. 108cm2 C. 180cm2 D. 90cm2
5.(泰安新泰市期末)下列说法中,错误的是( )
A. 在△ABC中,∠C=∠A-∠B,则△ABC为直角三角形
B. 在△ABC中,若∠A:∠B:∠C=5:2:3,则△ABC为直角三角形
C. 在△ABC中,若a=c,b=c,则△ABC为直角三角形
D. 在△ABC中,若a:b:c=3:2:4,则△ABC为直角三角形
考点3 勾股定理的应用
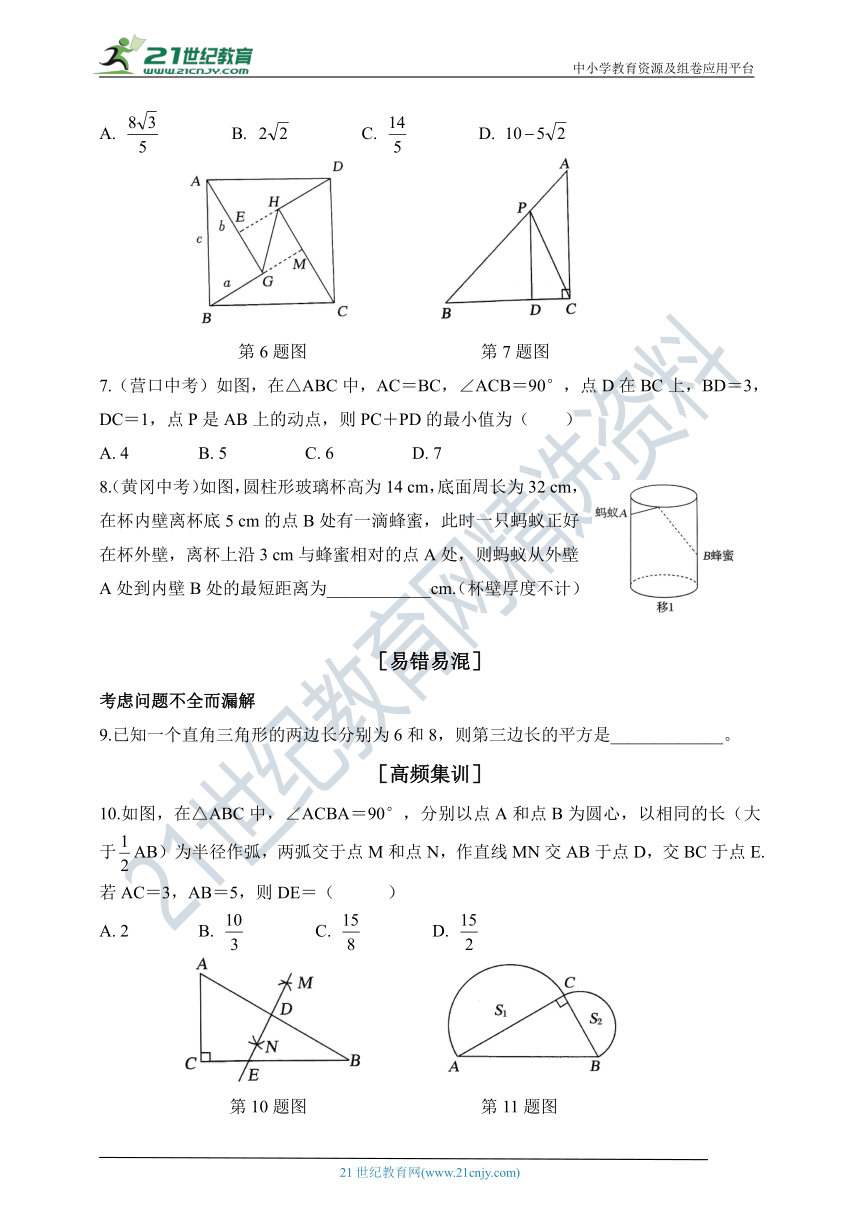
6.如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为( )
A. B. C. D.
第6题图 第7题图
7.(营口中考)如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为( )
A. 4 B. 5 C. 6 D. 7
8.(黄冈中考)如图,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为____________cm.(杯壁厚度不计)
[易错易混]
考虑问题不全而漏解
9.已知一个直角三角形的两边长分别为6和8,则第三边长的平方是_____________。
[高频集训]
10.如图,在△ABC中,∠ACBA=90°,分别以点A和点B为圆心,以相同的长(大于AB)为半径作弧,两弧交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE=( )
A. 2 B. C. D.
第10题图 第11题图
11.(烟台芝罘区期末)如图,在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2=( )
2π B. 4π C. 8π D. 16π
12.(益阳中考)如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积。
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
①作AD⊥BC于点D,设BD=x,用含x的代数式表示CD;→②根据勾股定理,利用AD作为“桥梁”,建立方程模型求出x;→③利用勾股定理求出AD的长,再计算三角形的面积
13.如图,折叠长方形的一边AD,使点D落在BC边的点F处,已知AB=8 cm,BC=10 cm。
(1)求EC的长;
(1)求AE的长。
参考答案
A 2. B 3. A 4. A 5. D 6. B 7. B
20 9. 100或28
C 11. A
12.解:在△ABC中,AB=15,BC=14,AC=13.
设BD=x,则CD=14-x。
由勾股定理,得AD2=AB2-BD2=152-x2,AD2=AC2-CD2=132-(14-x)2
故152-x2=132-(14-x)2,解得x=9,所以AD=12.
所以S△ABC=BC·AD=×14×12=84.
13.解:(1)因为四边形ABCD为长方形,以AD=BC=10 cm,DC= AB=8 cm.
由折叠可得△ADE≌△AFE,所以AF=AD=10 cm,EF=ED。
设EF=ED=x,则EC=8-x。
在Rt△ABF中,由勾股定理,得BF===6cm,
所以FC=BC-BF=10-6=4 cm。
在Rt△EFC中,
由勾股定理,得x2=42+(8-x)2,解得x=5,8-x=3。
所以EC的长为3 cm。
(2)在Rt△ADE中,
由勾股定理,得AE===5cm。
_21?????????è?????(www.21cnjy.com)_
第三章 勾股定理
章末复习
[考点突破]
考点1 勾股定理及其验证
1.(淄博校级期中联考)如图,在Rt△ABC中,∠C=90°,D为AC上一点,且DA=DB=5.如果△DAB的面积为10,那么DC的长是( )
A. 3 B. 4 C. 5 D. 6
第1题图 第2题图
2.如图是一张直角三角形的纸片,两直角边分别为AC=6 cm,BC=8 cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
A. 4 cm B. 5 cm C. 6 cm D. 10 cm
考点2 直角三角形的判定
3.(南通中考)下列长度的三条线段能组成直角三角形的是( )
A. 3,4,5 B. 2,3,4 C. 4,6,7 D. 5,11,12
4.(泰安新泰市月考)在△ABC中,AB=12 cm,AC=9 cm,BC=15 cm,则S△ABC为( )
A. 54cm2 B. 108cm2 C. 180cm2 D. 90cm2
5.(泰安新泰市期末)下列说法中,错误的是( )
A. 在△ABC中,∠C=∠A-∠B,则△ABC为直角三角形
B. 在△ABC中,若∠A:∠B:∠C=5:2:3,则△ABC为直角三角形
C. 在△ABC中,若a=c,b=c,则△ABC为直角三角形
D. 在△ABC中,若a:b:c=3:2:4,则△ABC为直角三角形
考点3 勾股定理的应用
6.如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为( )
A. B. C. D.
第6题图 第7题图
7.(营口中考)如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为( )
A. 4 B. 5 C. 6 D. 7
8.(黄冈中考)如图,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为____________cm.(杯壁厚度不计)
[易错易混]
考虑问题不全而漏解
9.已知一个直角三角形的两边长分别为6和8,则第三边长的平方是_____________。
[高频集训]
10.如图,在△ABC中,∠ACBA=90°,分别以点A和点B为圆心,以相同的长(大于AB)为半径作弧,两弧交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE=( )
A. 2 B. C. D.
第10题图 第11题图
11.(烟台芝罘区期末)如图,在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2=( )
2π B. 4π C. 8π D. 16π
12.(益阳中考)如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积。
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
①作AD⊥BC于点D,设BD=x,用含x的代数式表示CD;→②根据勾股定理,利用AD作为“桥梁”,建立方程模型求出x;→③利用勾股定理求出AD的长,再计算三角形的面积
13.如图,折叠长方形的一边AD,使点D落在BC边的点F处,已知AB=8 cm,BC=10 cm。
(1)求EC的长;
(1)求AE的长。
参考答案
A 2. B 3. A 4. A 5. D 6. B 7. B
20 9. 100或28
C 11. A
12.解:在△ABC中,AB=15,BC=14,AC=13.
设BD=x,则CD=14-x。
由勾股定理,得AD2=AB2-BD2=152-x2,AD2=AC2-CD2=132-(14-x)2
故152-x2=132-(14-x)2,解得x=9,所以AD=12.
所以S△ABC=BC·AD=×14×12=84.
13.解:(1)因为四边形ABCD为长方形,以AD=BC=10 cm,DC= AB=8 cm.
由折叠可得△ADE≌△AFE,所以AF=AD=10 cm,EF=ED。
设EF=ED=x,则EC=8-x。
在Rt△ABF中,由勾股定理,得BF===6cm,
所以FC=BC-BF=10-6=4 cm。
在Rt△EFC中,
由勾股定理,得x2=42+(8-x)2,解得x=5,8-x=3。
所以EC的长为3 cm。
(2)在Rt△ADE中,
由勾股定理,得AE===5cm。
_21?????????è?????(www.21cnjy.com)_
