轴对称(第2课时)线段的垂直平分线
文档属性
| 名称 | 轴对称(第2课时)线段的垂直平分线 |

|
|
| 格式 | rar | ||
| 文件大小 | 92.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-11 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
12.1 线段的垂直平分线
如图,直线L垂直平分AB,p1,p2,p3…是L上的点,分别量一量p1,p2,p3…到A与B的距离,你有什么发现?
A
B
P1
P2
P3
线段垂直平分线上的点与这条线段两个端点的距离相等。
A
B
P
C
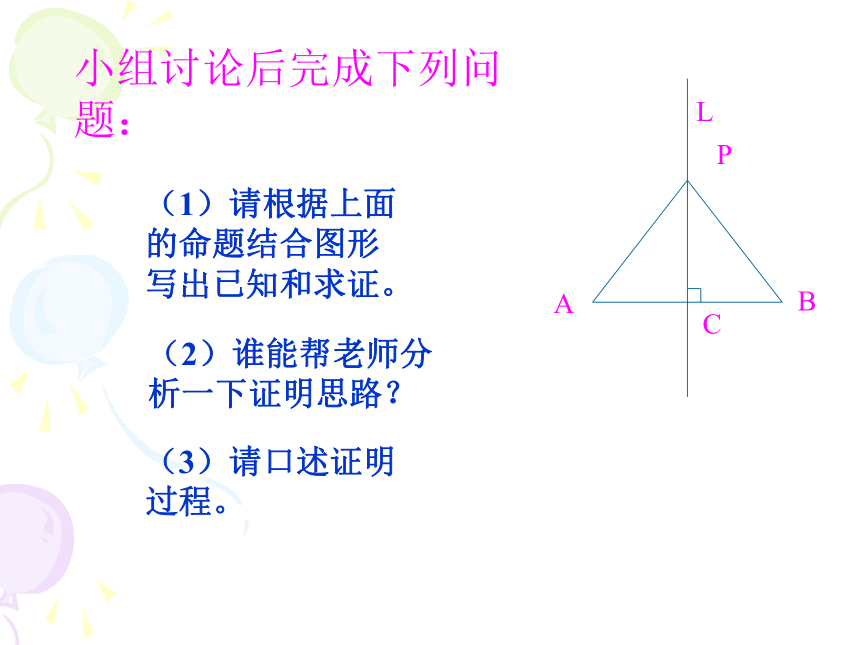
小组讨论后完成下列问题:
(1)请根据上面的命题结合图形写出已知和求证。
(2)谁能帮老师分析一下证明思路?
(3)请口述证明过程。
L
线段垂直平分线的性质定理:
线段垂直平分线上的点与这条线段两个端点的距离相等。
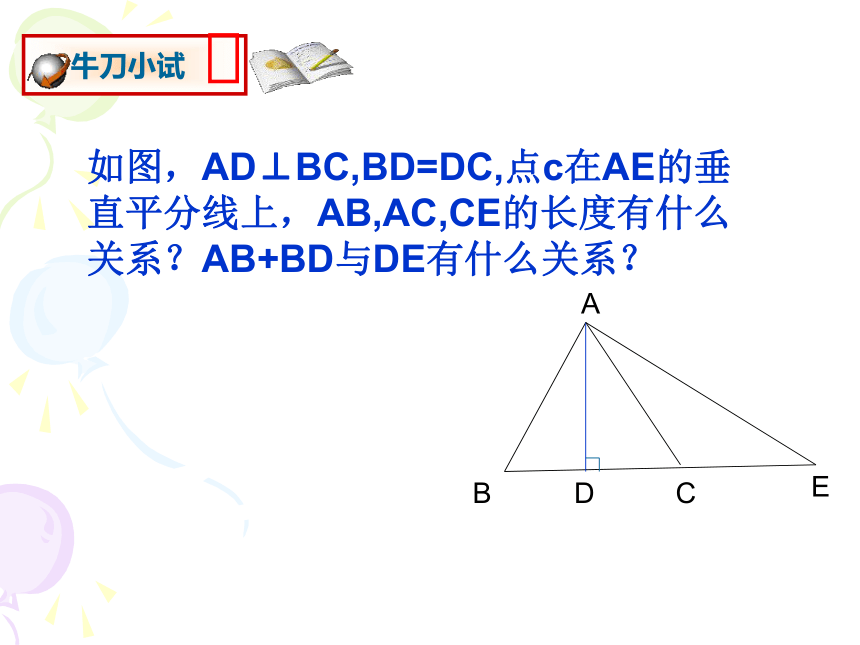
牛刀小试
如图,AD⊥BC,BD=DC,点c在AE的垂直平分线上,AB,AC,CE的长度有什么关系?AB+BD与DE有什么关系?
E
A
D
C
B
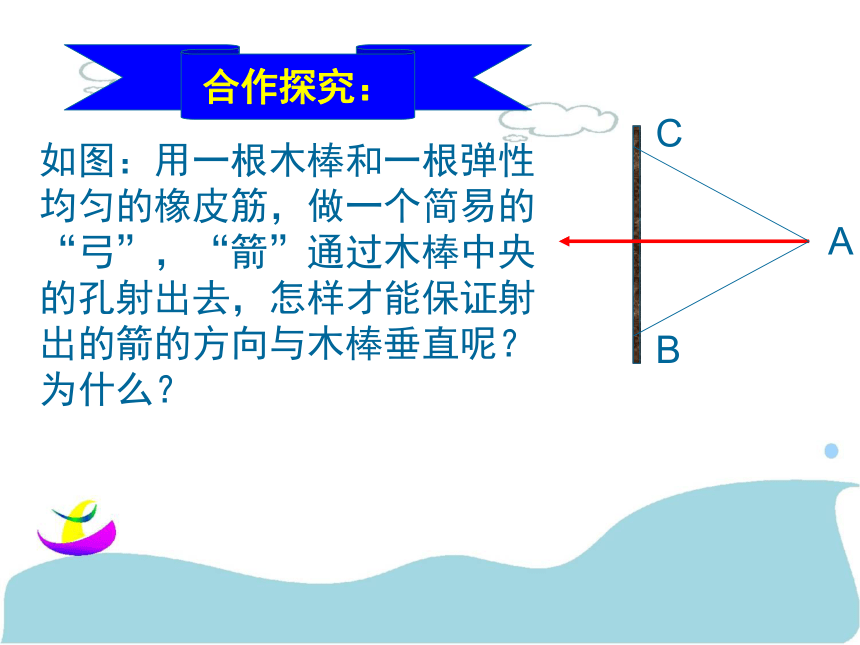
合作探究:
如图:用一根木棒和一根弹性均匀的橡皮筋,做一个简易的“弓”,“箭”通过木棒中央的孔射出去,怎样才能保证射出的箭的方向与木棒垂直呢?为什么?
A
C
B
结论:
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
你能证明这个结论吗?
已知:PA=PB,
求证:点P在线段AB的垂直平分线上。
B
P
A
C
线段垂直平分线的判定定理:
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
性质定理:线段垂直平分线上的点与线段两个
端点距离都相等。
判定定理:与线段两个端点距离相等的点都在
线段的垂直平分线上。
辨析:
A
B
P1
P2
P3
P4
P5
P6
O
·
·
·
·
·
·
·
●线段垂直平分线可以看作是与线段两个端点距离相等的所有点的集合。
线段垂直平分线的集合定义:
如图:AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
A
B
C
M
开启智慧
已知:如图, ΔABC 中,边 AB、BC 的垂直平分线相交于点 P.
求证:(1)PA=PB=PC;(2)P 在边 AC 的垂直平分线上.
A
B
C
P
通过本节课的学习,你有哪些收获?还有什么困惑?
课本P34练习1、2题。
12.1 线段的垂直平分线
如图,直线L垂直平分AB,p1,p2,p3…是L上的点,分别量一量p1,p2,p3…到A与B的距离,你有什么发现?
A
B
P1
P2
P3
线段垂直平分线上的点与这条线段两个端点的距离相等。
A
B
P
C
小组讨论后完成下列问题:
(1)请根据上面的命题结合图形写出已知和求证。
(2)谁能帮老师分析一下证明思路?
(3)请口述证明过程。
L
线段垂直平分线的性质定理:
线段垂直平分线上的点与这条线段两个端点的距离相等。
牛刀小试
如图,AD⊥BC,BD=DC,点c在AE的垂直平分线上,AB,AC,CE的长度有什么关系?AB+BD与DE有什么关系?
E
A
D
C
B
合作探究:
如图:用一根木棒和一根弹性均匀的橡皮筋,做一个简易的“弓”,“箭”通过木棒中央的孔射出去,怎样才能保证射出的箭的方向与木棒垂直呢?为什么?
A
C
B
结论:
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
你能证明这个结论吗?
已知:PA=PB,
求证:点P在线段AB的垂直平分线上。
B
P
A
C
线段垂直平分线的判定定理:
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
性质定理:线段垂直平分线上的点与线段两个
端点距离都相等。
判定定理:与线段两个端点距离相等的点都在
线段的垂直平分线上。
辨析:
A
B
P1
P2
P3
P4
P5
P6
O
·
·
·
·
·
·
·
●线段垂直平分线可以看作是与线段两个端点距离相等的所有点的集合。
线段垂直平分线的集合定义:
如图:AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
A
B
C
M
开启智慧
已知:如图, ΔABC 中,边 AB、BC 的垂直平分线相交于点 P.
求证:(1)PA=PB=PC;(2)P 在边 AC 的垂直平分线上.
A
B
C
P
通过本节课的学习,你有哪些收获?还有什么困惑?
课本P34练习1、2题。
