北师大版九年级数学下册3.2 圆的对称性同步试卷(Word版含答案)
文档属性
| 名称 | 北师大版九年级数学下册3.2 圆的对称性同步试卷(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 539.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-28 15:33:09 | ||
图片预览


文档简介
北师大版九年级数学下第三章2
圆的对称性(含答案)
一、选择题
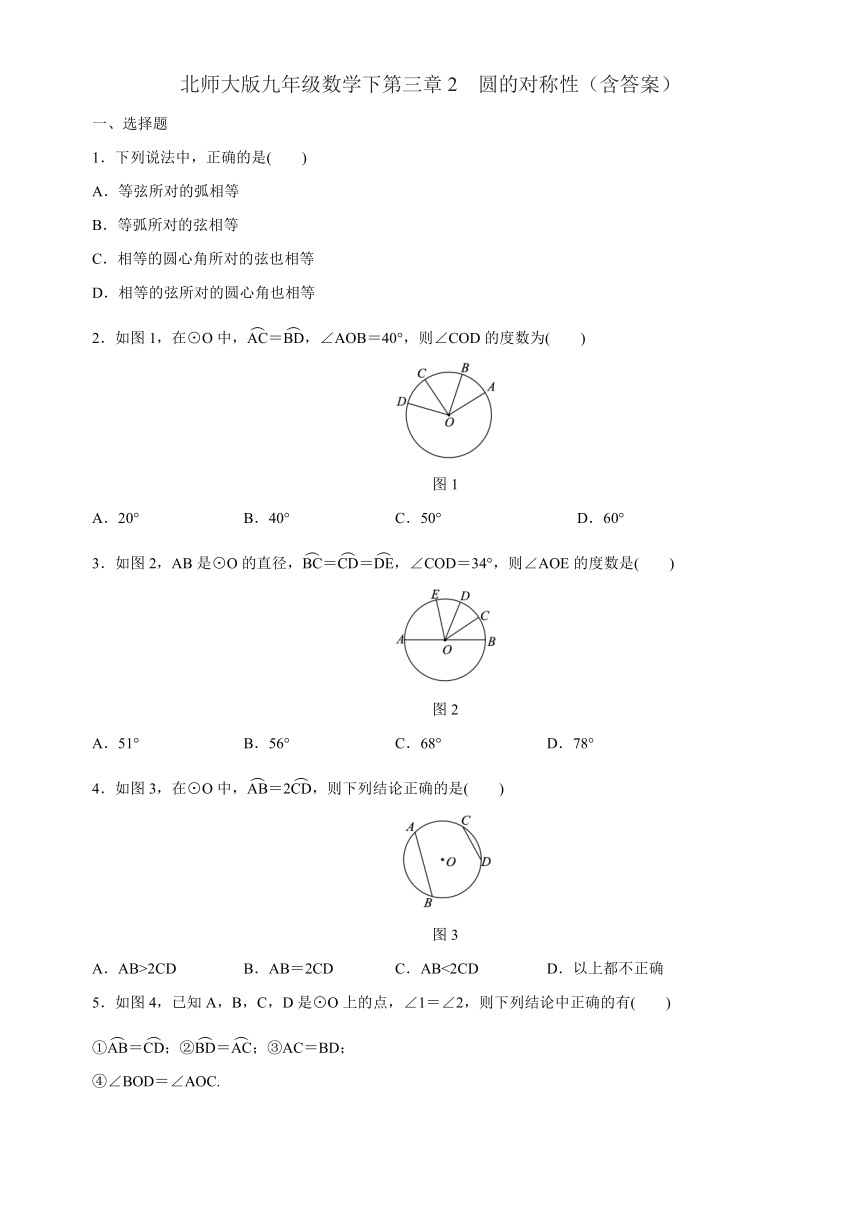
1.下列说法中,正确的是( )
A.等弦所对的弧相等
B.等弧所对的弦相等
C.相等的圆心角所对的弦也相等
D.相等的弦所对的圆心角也相等
2.如图1,在⊙O中,=,∠AOB=40°,则∠COD的度数为( )
图1
A.20°
B.40°
C.50°
D.60°
3.如图2,AB是⊙O的直径,==,∠COD=34°,则∠AOE的度数是( )
图2
A.51°
B.56°
C.68°
D.78°
4.如图3,在⊙O中,=2,则下列结论正确的是( )
图3
A.AB>2CD
B.AB=2CD
C.AB<2CD
D.以上都不正确
5.如图4,已知A,B,C,D是⊙O上的点,∠1=∠2,则下列结论中正确的有( )
①=;②=;③AC=BD;
④∠BOD=∠AOC.
图4
A.1个
B.2个
C.3个
D.4个
二、填空题
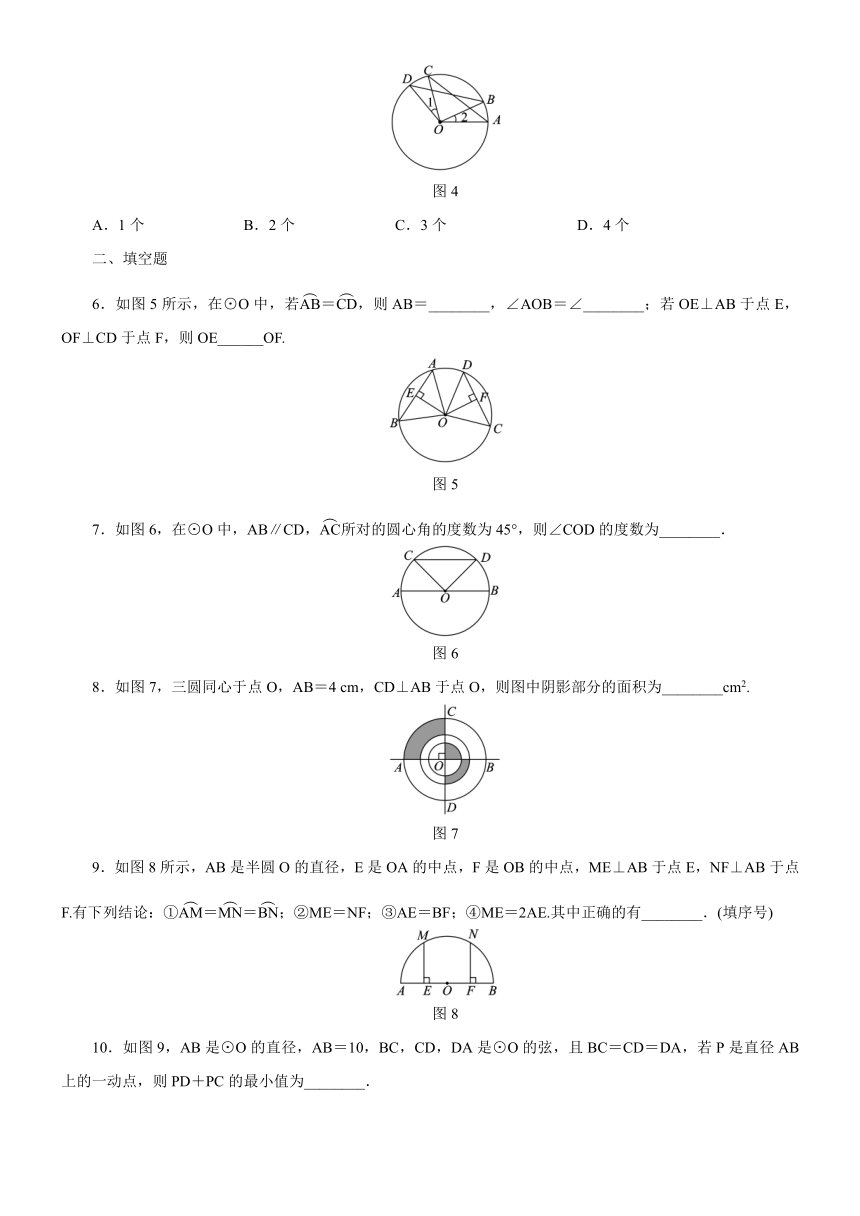
6.如图5所示,在⊙O中,若=,则AB=________,∠AOB=∠________;若OE⊥AB于点E,OF⊥CD于点F,则OE______OF.
图5
7.如图6,在⊙O中,AB∥CD,所对的圆心角的度数为45°,则∠COD的度数为________.
图6
8.如图7,三圆同心于点O,AB=4
cm,CD⊥AB于点O,则图中阴影部分的面积为________cm2.
图7
9.如图8所示,AB是半圆O的直径,E是OA的中点,F是OB的中点,ME⊥AB于点E,NF⊥AB于点F.有下列结论:①==;②ME=NF;③AE=BF;④ME=2AE.其中正确的有________.(填序号)
图8
10.如图9,AB是⊙O的直径,AB=10,BC,CD,DA是⊙O的弦,且BC=CD=DA,若P是直径AB上的一动点,则PD+PC的最小值为________.
图9
三、解答题
11.如图10,在⊙O中,=.
求证:∠B=∠C.
图10
12.如图11所示,以?ABCD的顶点A为圆心,AB的长为半径作圆,与AD,BC分别交于点E,F,延长BA交⊙A于点G.求证:=.
图11
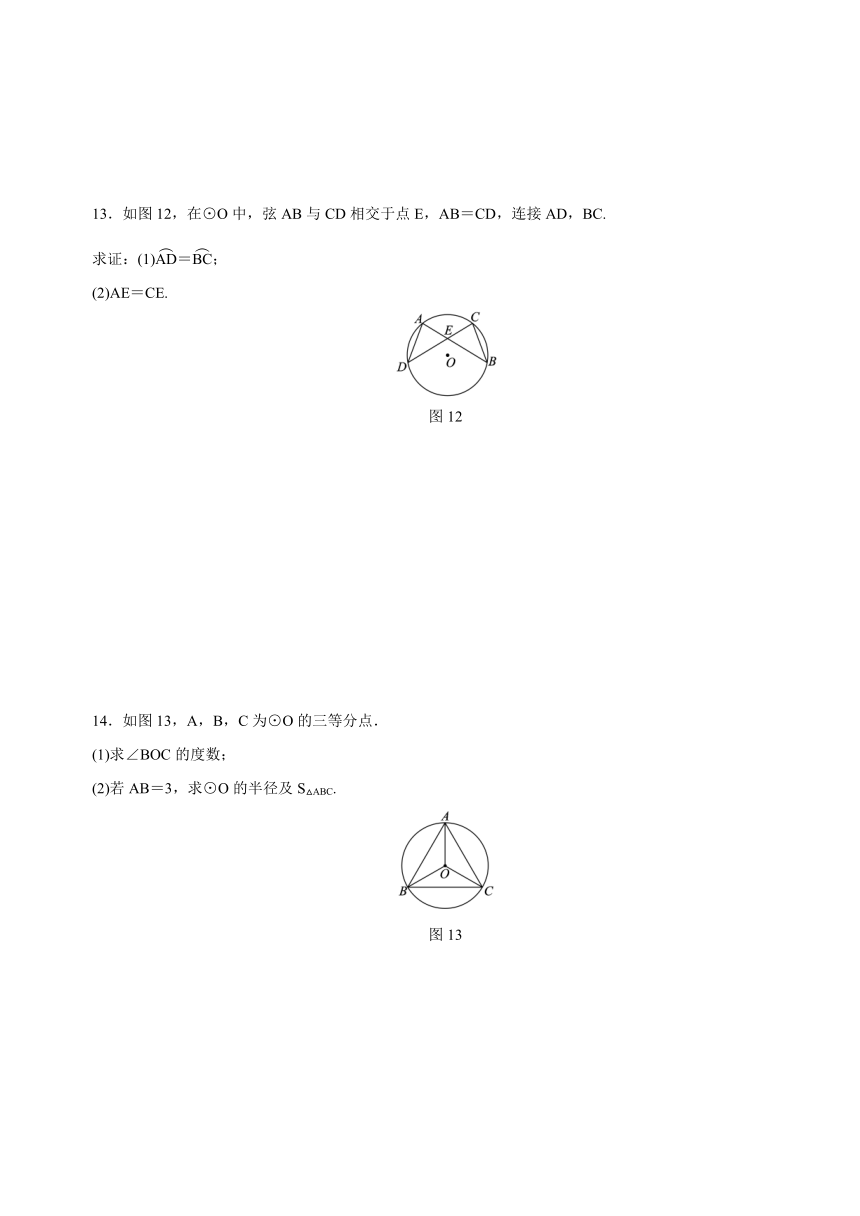
13.如图12,在⊙O中,弦AB与CD相交于点E,AB=CD,连接AD,BC.
求证:(1)=;
(2)AE=CE.
图12
14.如图13,A,B,C为⊙O的三等分点.
(1)求∠BOC的度数;
(2)若AB=3,求⊙O的半径及S△ABC.
图13
附加题
我们学习了弧、弦、圆心角之间的关系,实际上我们还可以得到圆心角、弧、弦、弦心距之间的关系如下:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等[弦心距指从圆心到弦的距离(如图14①中的OC,OC′),弦心距也可以说成圆心到弦的垂线段的长度].请直接运用圆心角、弧、弦、弦心距之间的关系解答下列问题:
如图②,O是∠EPF的平分线上一点,以点O为圆心的圆与角的两边分别交于点A,B和C,D.
(1)求证:AB=CD.
(2)若角的顶点P在圆上,上述结论还成立吗?若不成立,请说明理由;若成立,请加以证明.
图14
参考答案
1.[解析]
B “在同圆或等圆中”是弧、弦、圆心角的关系定理成立的前提条件,不可忽视.以上选项中只有“等弧”满足该条件,所以B正确.
2.[解析]
B ∵=,∴=,∴∠AOB=∠COD.∵∠AOB=40°,∴∠COD=40°.故选B.
3.[解析]
D ∵==,∠COD=34°,∴∠BOC=∠EOD=∠COD=34°,∴∠AOE=180°-∠EOD-∠COD-∠BOC=78°.
4.[解析]
C 如图,取的中点E,连接AE,BE.
∵在⊙O中,=2,
∴==,
∴AE=BE=CD.
∵AE+BE>AB,
∴2CD>AB.故选C.
5.[答案]
D
6.[答案]
CD COD =
7.[答案]
90°
8.[答案]
π
[解析]
AB=4
cm,CO⊥AB于点O,则OA=2
cm.根据圆的旋转不变性,把最小的圆逆时针旋转90°,把中间圆旋转180°,则阴影部分就合成了扇形OAC,即圆的,∴阴影部分的面积为×π×22=π(cm2).
9.[答案]
①②③
10.[答案]
10
[解析]
如图,作点C关于AB的对称点C′,连接OC,OD,OC′,BC′.∵BC=CD=DA,∴∠AOD=∠COD=∠BOC=60°.∵点C与点C′关于AB对称,∴BC′=BC,∴∠BOC′=60°,∴点D,O,C′在同一条直线上,∴DC′=AB=10,即PD+PC的最小值为10.
11.证明:∵在⊙O中,=,
∴∠AOB=∠COD.
∵OA=OB,OC=OD,
∴在△AOB中,∠B=90°-∠AOB,在△COD中,∠C=90°-∠COD,
∴∠B=∠C.
12.证明:如图,连接AF.
∵AB=AF,
∴∠ABF=∠AFB.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAF=∠AFB,∠GAE=∠ABF,
∴∠GAE=∠EAF,
∴=.
13.证明:(1)∵AB=CD,∴=,
∴-=-,
∴=.
(2)如图,连接AC.
∵=,
∴AD=BC.
在△ABC和△CDA中,
∵AB=CD,BC=DA,AC=CA,
∴△ABC≌△CDA,
∴∠BAC=∠DCA,
∴AE=CE.
14.解:(1)∵A,B,C为⊙O的三等分点,
∴==,
∴∠BOC=×360°=120°.
(2)过点O作OD⊥AB于点D.
∵A,B,C为⊙O的三等分点,
∴AB=AC=BC=3,
即△ABC是等边三角形,
∴∠BAO=∠OBA=30°,
则AD=,故OD=,OA=,
即⊙O的半径为.
S△ABC=3S△ABO=3×OD·AB=.
附加题
解:(1)证明:如图,过点O作OM⊥AB于点M,ON⊥CD于点N,
则∠OMP=∠ONP=90°.
∵PO平分∠EPF,
∴OM=ON.
∵OM,ON分别是弦AB,CD的弦心距,
∴AB=CD.
(2)上述结论成立.
证明:若点P在⊙O上,过点O作OM⊥AB于点M,ON⊥CD于点N.同(1)可得OM=ON.
∵OM,ON分别是弦AB,CD的弦心距,
∴AB=CD.
圆的对称性(含答案)
一、选择题
1.下列说法中,正确的是( )
A.等弦所对的弧相等
B.等弧所对的弦相等
C.相等的圆心角所对的弦也相等
D.相等的弦所对的圆心角也相等
2.如图1,在⊙O中,=,∠AOB=40°,则∠COD的度数为( )
图1
A.20°
B.40°
C.50°
D.60°
3.如图2,AB是⊙O的直径,==,∠COD=34°,则∠AOE的度数是( )
图2
A.51°
B.56°
C.68°
D.78°
4.如图3,在⊙O中,=2,则下列结论正确的是( )
图3
A.AB>2CD
B.AB=2CD
C.AB<2CD
D.以上都不正确
5.如图4,已知A,B,C,D是⊙O上的点,∠1=∠2,则下列结论中正确的有( )
①=;②=;③AC=BD;
④∠BOD=∠AOC.
图4
A.1个
B.2个
C.3个
D.4个
二、填空题
6.如图5所示,在⊙O中,若=,则AB=________,∠AOB=∠________;若OE⊥AB于点E,OF⊥CD于点F,则OE______OF.
图5
7.如图6,在⊙O中,AB∥CD,所对的圆心角的度数为45°,则∠COD的度数为________.
图6
8.如图7,三圆同心于点O,AB=4
cm,CD⊥AB于点O,则图中阴影部分的面积为________cm2.
图7
9.如图8所示,AB是半圆O的直径,E是OA的中点,F是OB的中点,ME⊥AB于点E,NF⊥AB于点F.有下列结论:①==;②ME=NF;③AE=BF;④ME=2AE.其中正确的有________.(填序号)
图8
10.如图9,AB是⊙O的直径,AB=10,BC,CD,DA是⊙O的弦,且BC=CD=DA,若P是直径AB上的一动点,则PD+PC的最小值为________.
图9
三、解答题
11.如图10,在⊙O中,=.
求证:∠B=∠C.
图10
12.如图11所示,以?ABCD的顶点A为圆心,AB的长为半径作圆,与AD,BC分别交于点E,F,延长BA交⊙A于点G.求证:=.
图11
13.如图12,在⊙O中,弦AB与CD相交于点E,AB=CD,连接AD,BC.
求证:(1)=;
(2)AE=CE.
图12
14.如图13,A,B,C为⊙O的三等分点.
(1)求∠BOC的度数;
(2)若AB=3,求⊙O的半径及S△ABC.
图13
附加题
我们学习了弧、弦、圆心角之间的关系,实际上我们还可以得到圆心角、弧、弦、弦心距之间的关系如下:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等[弦心距指从圆心到弦的距离(如图14①中的OC,OC′),弦心距也可以说成圆心到弦的垂线段的长度].请直接运用圆心角、弧、弦、弦心距之间的关系解答下列问题:
如图②,O是∠EPF的平分线上一点,以点O为圆心的圆与角的两边分别交于点A,B和C,D.
(1)求证:AB=CD.
(2)若角的顶点P在圆上,上述结论还成立吗?若不成立,请说明理由;若成立,请加以证明.
图14
参考答案
1.[解析]
B “在同圆或等圆中”是弧、弦、圆心角的关系定理成立的前提条件,不可忽视.以上选项中只有“等弧”满足该条件,所以B正确.
2.[解析]
B ∵=,∴=,∴∠AOB=∠COD.∵∠AOB=40°,∴∠COD=40°.故选B.
3.[解析]
D ∵==,∠COD=34°,∴∠BOC=∠EOD=∠COD=34°,∴∠AOE=180°-∠EOD-∠COD-∠BOC=78°.
4.[解析]
C 如图,取的中点E,连接AE,BE.
∵在⊙O中,=2,
∴==,
∴AE=BE=CD.
∵AE+BE>AB,
∴2CD>AB.故选C.
5.[答案]
D
6.[答案]
CD COD =
7.[答案]
90°
8.[答案]
π
[解析]
AB=4
cm,CO⊥AB于点O,则OA=2
cm.根据圆的旋转不变性,把最小的圆逆时针旋转90°,把中间圆旋转180°,则阴影部分就合成了扇形OAC,即圆的,∴阴影部分的面积为×π×22=π(cm2).
9.[答案]
①②③
10.[答案]
10
[解析]
如图,作点C关于AB的对称点C′,连接OC,OD,OC′,BC′.∵BC=CD=DA,∴∠AOD=∠COD=∠BOC=60°.∵点C与点C′关于AB对称,∴BC′=BC,∴∠BOC′=60°,∴点D,O,C′在同一条直线上,∴DC′=AB=10,即PD+PC的最小值为10.
11.证明:∵在⊙O中,=,
∴∠AOB=∠COD.
∵OA=OB,OC=OD,
∴在△AOB中,∠B=90°-∠AOB,在△COD中,∠C=90°-∠COD,
∴∠B=∠C.
12.证明:如图,连接AF.
∵AB=AF,
∴∠ABF=∠AFB.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAF=∠AFB,∠GAE=∠ABF,
∴∠GAE=∠EAF,
∴=.
13.证明:(1)∵AB=CD,∴=,
∴-=-,
∴=.
(2)如图,连接AC.
∵=,
∴AD=BC.
在△ABC和△CDA中,
∵AB=CD,BC=DA,AC=CA,
∴△ABC≌△CDA,
∴∠BAC=∠DCA,
∴AE=CE.
14.解:(1)∵A,B,C为⊙O的三等分点,
∴==,
∴∠BOC=×360°=120°.
(2)过点O作OD⊥AB于点D.
∵A,B,C为⊙O的三等分点,
∴AB=AC=BC=3,
即△ABC是等边三角形,
∴∠BAO=∠OBA=30°,
则AD=,故OD=,OA=,
即⊙O的半径为.
S△ABC=3S△ABO=3×OD·AB=.
附加题
解:(1)证明:如图,过点O作OM⊥AB于点M,ON⊥CD于点N,
则∠OMP=∠ONP=90°.
∵PO平分∠EPF,
∴OM=ON.
∵OM,ON分别是弦AB,CD的弦心距,
∴AB=CD.
(2)上述结论成立.
证明:若点P在⊙O上,过点O作OM⊥AB于点M,ON⊥CD于点N.同(1)可得OM=ON.
∵OM,ON分别是弦AB,CD的弦心距,
∴AB=CD.
