多边形的内角和
图片预览








文档简介
(共38张PPT)
生活中的平面图形
三角形
长方形
四边形
六边形
八边形
五边形
边
内角
顶点
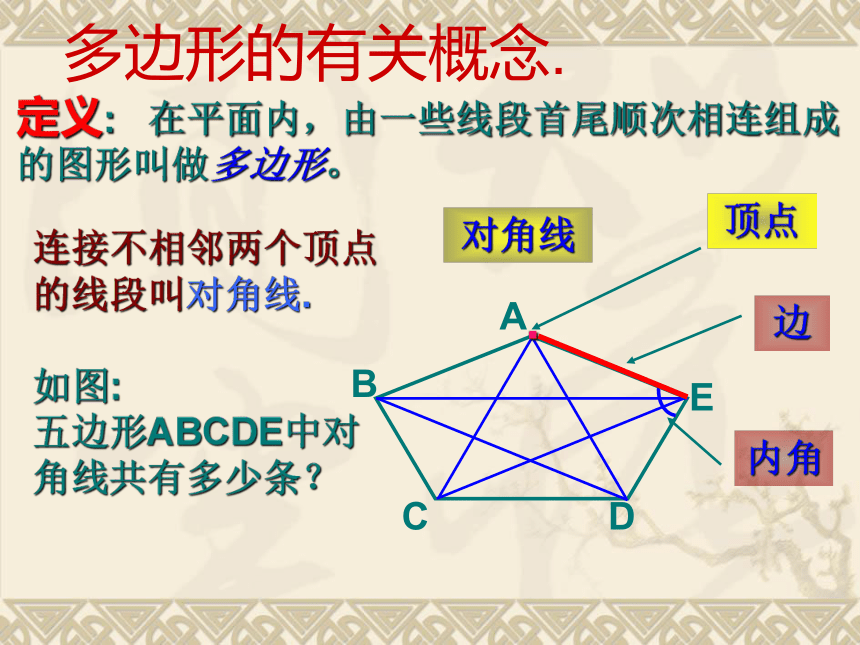
定义: 在平面内,由一些线段首尾顺次相连组成的图形叫做多边形。
对角线
连接不相邻两个顶点的线段叫对角线.
如图:
五边形ABCDE中对角线共有多少条?
多边形的有关概念.
D
B
A
E
C
.
探索多边形的内角和
这个五边形的内角和应该怎么求呢?
你有几种方法呢?
A
C
D
E
B
过多边形任一顶点有多少条对角线?这些对角线将多边形分成多少个三角形?
多边形
三角形 四边形 五边形 六边形 … n边形
对角线
条数 …
三角形
个数 …
0
1
1
2
2
3
3
4
n-3
n-2
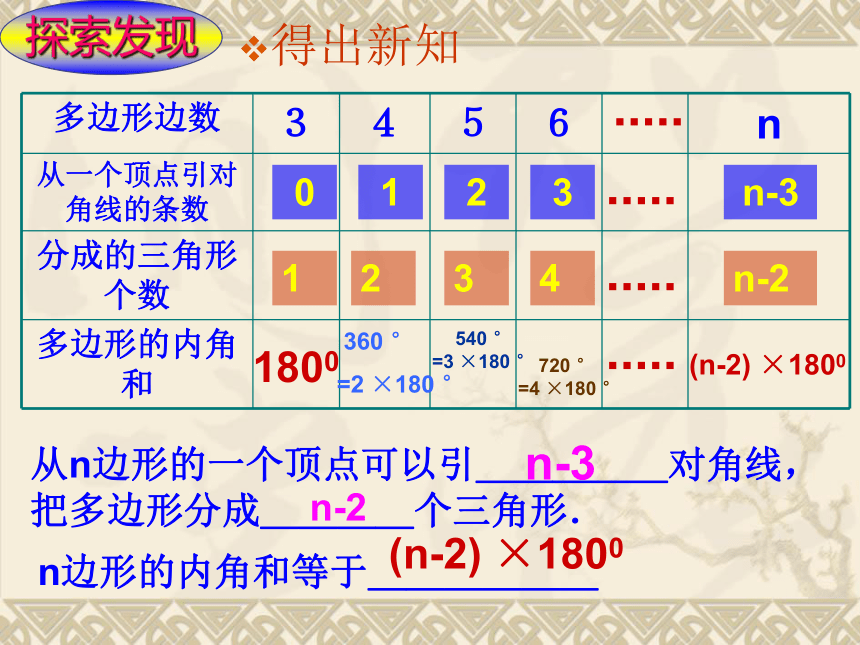
得出新知
探索发现
多边形边数 3 4 5 6 n
从一个顶点引对角线的条数
分成的三角形个数
多边形的内角和
n-2
3
2
1
0
4
3
2
1
n-3
1800
360 °
=2 ×180 °
540 °
=3 ×180 °
720 °
=4 ×180 °
(n-2) ×1800
从n边形的一个顶点可以引_____对角线,把多边形分成____个三角形.
n边形的内角和等于______
n-3
n-2
(n-2) ×1800
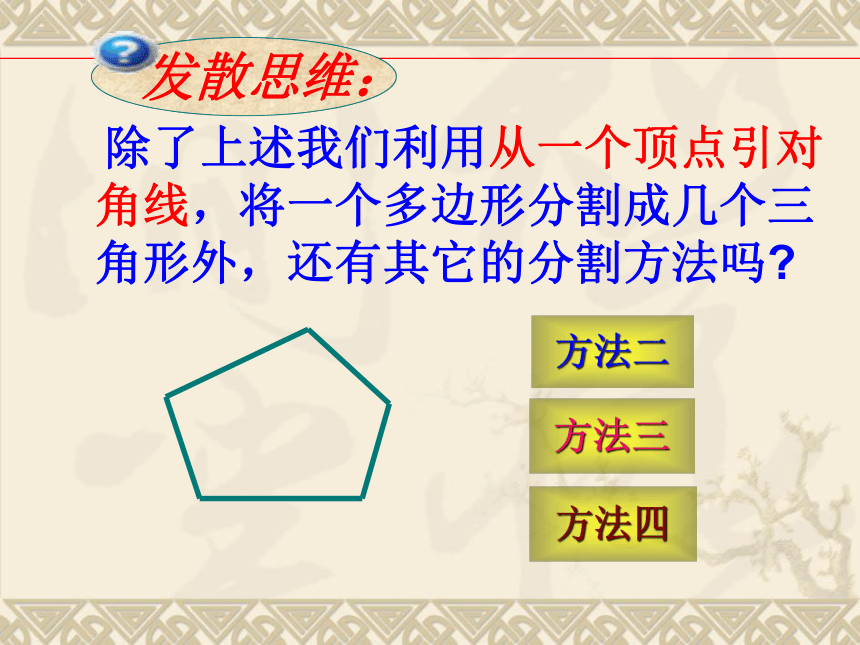
除了上述我们利用从一个顶点引对角线,将一个多边形分割成几个三角形外,还有其它的分割方法吗
发散思维:
方法二
方法三
方法四
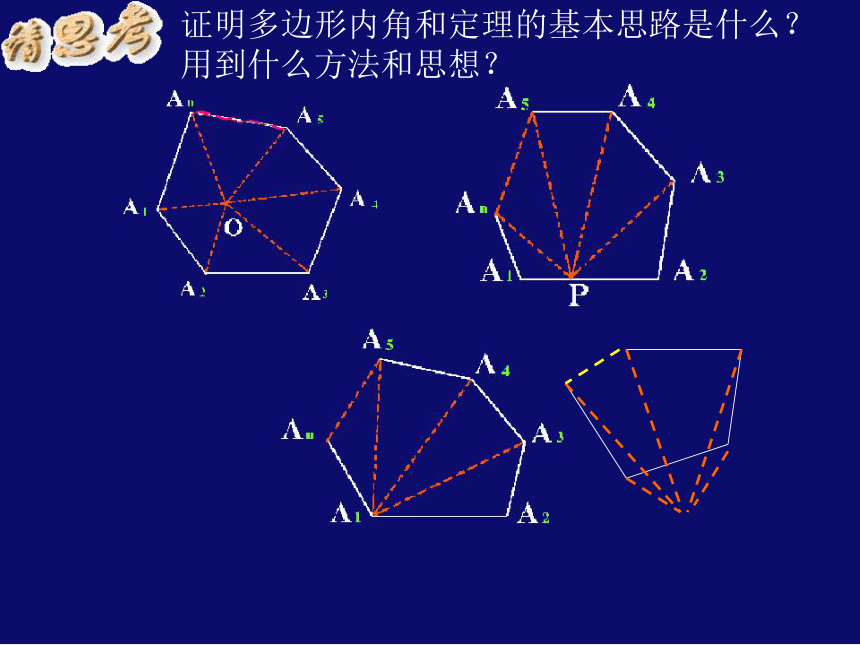
证明多边形内角和定理的基本思路是什么?
用到什么方法和思想?
1、思路:多边形问题转化为
三角形的问题来解决。
2、 转化的方法;
从特殊到一般的研究方法。
3、 化归思想:
化多边形问题为三角形问题来解.
4、用多种方法解决问题。
n边形内角和公式的应用
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解:
如图,四边形ABCD中,
∠A+ ∠C =180°
∠A+∠B+∠C+∠D=(4-2) ×180 °
= 360 °
因为
∠B+∠D
= 360°-(∠A+∠C)
= 360°- 180°
=180°
这就是说:如果四边形一组对角互补,那么另一组对角也互补.
所以
小试身手 :
已知一个多边形,它的内角和 等于720°, 求这个多边形的边数。
解: 设多边形的边数为n,因为它的内角和等于 (n-2) 180°,
所以, (n-2) 180°= 720 。
解得: n=6
这个多边形的边数为6。
现学现用.
已知一个多边形,它的内角和 等于五边形的 内角和的2倍,求这个多边形的边数。
解: 设多边形的边数为n,
因为它的内角和等于 (n-2) 180°,
五边形内角和等于540 ,所以,
(n-2) 180°=2×540 。
解得: n=8
这个多边形的边数8。
举一反三.
1、求十边形的内角和的度数。
快速反应:
解:(10-2)×180°=8 ×180°=1440°
答:十边形的内角和是1440°
4、求下列图形中 x的值
3.已知一个多边形的内角和为1080°,
则它的边数为_____。
2.(a+1)边形的内角和是____________.
(a -1)×180°
8
X= 60°
X= 95°
如图,求∠A+∠B + ∠C + ∠D + ∠ E + ∠F + ∠G 的度数。
A
B
C
D
E
F
G
A
B
C
D
E
A
B
C
D
E
解: (5-2)×180°=3×180°=540°
①
A
B
C
D
②
E
F
③
M
N
话说三国时期,刘备等人商讨大事。不知谁惹恼刘备,怒执其剑说道:谁再敢胡言,有如此案。便一剑削下。
问削完后,桌子是几边形。
2.正方形每个角的度数为_____。
3.已知一个多边形的每一个内角都是144°, 则它的边数为______。
1.等边三角形每个角的度数为_____。
60°
90°
观察图中的多边形,他们的边、角有什么特点?
定义: 在平面内,内角都相等、边也相等的多边形叫做正多边形。
正多边形每个内角:
(n-2) ·180
n
正多边形的内角和: (n-2)×180°
n ·α
(α为一个内角)
议一议:
(1)一个多边形的边都相等,它的内角一定都相等吗?
(2)一个多边形的内角都相等,它的边一定都相等吗?
(3)正三角形、正四边形(正方形)、正五边形、正六边形、正八边形的每个内角分别是多少度?
(不一定,如菱形的边都相等,但内角不一定相等)
(不一定,如矩形的内角都相等,但边未必都相等)
60
90
120
108
135
1.多边形的内角和随着边数的增加而 ,
边数增加一条时,它的内角和增加 度 .
2、正十边形的每一个内角的度数
是_____,每个外角度数为__。
144°
十二
练一练
增加
3、一个多边形的每一个内角为150°。
这是_____边形,每个外角度数为__。
(填正十二边对吗?)
36°
30°
180°
例1 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和他相邻的内角有什么关系?
2.五个外角加上他们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
6
E
B
C
D
1
2
3
4
5
A
例1 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
5边形外角和
结论:
五边形的外角和等于360°
-(5-2) × 180°
=360 °
6
E
B
C
D
1
2
3
4
5
A
=5个平角
-5边形内角和
=5×180°
探究在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和=
结论:
n边形的外角和等于360°
-(n-2) × 180°
=360 °
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180 °
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。
由于在这个运动过程中走了一周,也就是说所转的各个角的和等于一个周角。
即:多边形的外角和等于360
7.3.2 多边形的内角和
小练习:
1. 判断题:
(1)当多边形的边数增加时,它的外角和也随着增加。
(2)正六边形的每个外角都等于60度。
2. 填空题:
(1)正九边形的每一个外角都等于 度。
40
(2)一个多边形的每一个外角都等于30°,
这个多边形是 边形。
正十二
1.通过这节课的学习活动你有哪些收获?
2.你还有哪些困惑?
小 结
1、什么是多边形?
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。
2. n边形的内角和等于 (n - 2) 180°.
4. 过n边形的某一个顶点的所有对角线有几条?
被分成几个三角形?
有(n - 3) 条。
被分成(n - 2) 个。
3. 正多边形的定义、正多边形的每个内角度数的计算公式.
[(n-2) ·180 ]÷n .
5. 三种求多边形内角和的方法,体现了数学的化归思想:化多边形问题为三角形问题来解.
n ·α.
作业
一 p84-85 3、4、5
二 其它相关练习
E
A
B
C
D
O
探究2
180°× 5 – 360°= 540°
180°× 5=900°?
五边形内角和540°??
返回
A
E
D
C
B
O
O
O
180°× 5 – 360°= 540°
180°× 4 – 360°= 360°
180°× 6 – 360°= 720°
返回
n边形 : 180 ×n– 360°
= 180 ×n– 180 ×2 = (n-2) ·180
把一个五边形分成几个三角形,还有其他的分法吗?
A
B
C
D
E
F
180° × 4 – 180° = 540°
探究3
返回
A
B
C
D
E
F
180°× 3– 180° = 360°
180°× 4 – 180° = 540°
180°× 5 – 180° = 720°
返回
n边形 : 180 ×(n-1)– 180°= (n-2) ·180
探究4
A
B
C
D
E
4 × 180°-180 °
O
=540°
返回
B
C
D
E
180°× 3– 180° = 360°
180°× 4 – 180° = 540°
180°× 5 – 180° = 720°
返回
n边形 : 180 ×(n-1)– 180°= (n-2) ·180
生活中的平面图形
三角形
长方形
四边形
六边形
八边形
五边形
边
内角
顶点
定义: 在平面内,由一些线段首尾顺次相连组成的图形叫做多边形。
对角线
连接不相邻两个顶点的线段叫对角线.
如图:
五边形ABCDE中对角线共有多少条?
多边形的有关概念.
D
B
A
E
C
.
探索多边形的内角和
这个五边形的内角和应该怎么求呢?
你有几种方法呢?
A
C
D
E
B
过多边形任一顶点有多少条对角线?这些对角线将多边形分成多少个三角形?
多边形
三角形 四边形 五边形 六边形 … n边形
对角线
条数 …
三角形
个数 …
0
1
1
2
2
3
3
4
n-3
n-2
得出新知
探索发现
多边形边数 3 4 5 6 n
从一个顶点引对角线的条数
分成的三角形个数
多边形的内角和
n-2
3
2
1
0
4
3
2
1
n-3
1800
360 °
=2 ×180 °
540 °
=3 ×180 °
720 °
=4 ×180 °
(n-2) ×1800
从n边形的一个顶点可以引_____对角线,把多边形分成____个三角形.
n边形的内角和等于______
n-3
n-2
(n-2) ×1800
除了上述我们利用从一个顶点引对角线,将一个多边形分割成几个三角形外,还有其它的分割方法吗
发散思维:
方法二
方法三
方法四
证明多边形内角和定理的基本思路是什么?
用到什么方法和思想?
1、思路:多边形问题转化为
三角形的问题来解决。
2、 转化的方法;
从特殊到一般的研究方法。
3、 化归思想:
化多边形问题为三角形问题来解.
4、用多种方法解决问题。
n边形内角和公式的应用
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解:
如图,四边形ABCD中,
∠A+ ∠C =180°
∠A+∠B+∠C+∠D=(4-2) ×180 °
= 360 °
因为
∠B+∠D
= 360°-(∠A+∠C)
= 360°- 180°
=180°
这就是说:如果四边形一组对角互补,那么另一组对角也互补.
所以
小试身手 :
已知一个多边形,它的内角和 等于720°, 求这个多边形的边数。
解: 设多边形的边数为n,因为它的内角和等于 (n-2) 180°,
所以, (n-2) 180°= 720 。
解得: n=6
这个多边形的边数为6。
现学现用.
已知一个多边形,它的内角和 等于五边形的 内角和的2倍,求这个多边形的边数。
解: 设多边形的边数为n,
因为它的内角和等于 (n-2) 180°,
五边形内角和等于540 ,所以,
(n-2) 180°=2×540 。
解得: n=8
这个多边形的边数8。
举一反三.
1、求十边形的内角和的度数。
快速反应:
解:(10-2)×180°=8 ×180°=1440°
答:十边形的内角和是1440°
4、求下列图形中 x的值
3.已知一个多边形的内角和为1080°,
则它的边数为_____。
2.(a+1)边形的内角和是____________.
(a -1)×180°
8
X= 60°
X= 95°
如图,求∠A+∠B + ∠C + ∠D + ∠ E + ∠F + ∠G 的度数。
A
B
C
D
E
F
G
A
B
C
D
E
A
B
C
D
E
解: (5-2)×180°=3×180°=540°
①
A
B
C
D
②
E
F
③
M
N
话说三国时期,刘备等人商讨大事。不知谁惹恼刘备,怒执其剑说道:谁再敢胡言,有如此案。便一剑削下。
问削完后,桌子是几边形。
2.正方形每个角的度数为_____。
3.已知一个多边形的每一个内角都是144°, 则它的边数为______。
1.等边三角形每个角的度数为_____。
60°
90°
观察图中的多边形,他们的边、角有什么特点?
定义: 在平面内,内角都相等、边也相等的多边形叫做正多边形。
正多边形每个内角:
(n-2) ·180
n
正多边形的内角和: (n-2)×180°
n ·α
(α为一个内角)
议一议:
(1)一个多边形的边都相等,它的内角一定都相等吗?
(2)一个多边形的内角都相等,它的边一定都相等吗?
(3)正三角形、正四边形(正方形)、正五边形、正六边形、正八边形的每个内角分别是多少度?
(不一定,如菱形的边都相等,但内角不一定相等)
(不一定,如矩形的内角都相等,但边未必都相等)
60
90
120
108
135
1.多边形的内角和随着边数的增加而 ,
边数增加一条时,它的内角和增加 度 .
2、正十边形的每一个内角的度数
是_____,每个外角度数为__。
144°
十二
练一练
增加
3、一个多边形的每一个内角为150°。
这是_____边形,每个外角度数为__。
(填正十二边对吗?)
36°
30°
180°
例1 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和他相邻的内角有什么关系?
2.五个外角加上他们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
6
E
B
C
D
1
2
3
4
5
A
例1 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
5边形外角和
结论:
五边形的外角和等于360°
-(5-2) × 180°
=360 °
6
E
B
C
D
1
2
3
4
5
A
=5个平角
-5边形内角和
=5×180°
探究在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和=
结论:
n边形的外角和等于360°
-(n-2) × 180°
=360 °
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180 °
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。
由于在这个运动过程中走了一周,也就是说所转的各个角的和等于一个周角。
即:多边形的外角和等于360
7.3.2 多边形的内角和
小练习:
1. 判断题:
(1)当多边形的边数增加时,它的外角和也随着增加。
(2)正六边形的每个外角都等于60度。
2. 填空题:
(1)正九边形的每一个外角都等于 度。
40
(2)一个多边形的每一个外角都等于30°,
这个多边形是 边形。
正十二
1.通过这节课的学习活动你有哪些收获?
2.你还有哪些困惑?
小 结
1、什么是多边形?
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。
2. n边形的内角和等于 (n - 2) 180°.
4. 过n边形的某一个顶点的所有对角线有几条?
被分成几个三角形?
有(n - 3) 条。
被分成(n - 2) 个。
3. 正多边形的定义、正多边形的每个内角度数的计算公式.
[(n-2) ·180 ]÷n .
5. 三种求多边形内角和的方法,体现了数学的化归思想:化多边形问题为三角形问题来解.
n ·α.
作业
一 p84-85 3、4、5
二 其它相关练习
E
A
B
C
D
O
探究2
180°× 5 – 360°= 540°
180°× 5=900°?
五边形内角和540°??
返回
A
E
D
C
B
O
O
O
180°× 5 – 360°= 540°
180°× 4 – 360°= 360°
180°× 6 – 360°= 720°
返回
n边形 : 180 ×n– 360°
= 180 ×n– 180 ×2 = (n-2) ·180
把一个五边形分成几个三角形,还有其他的分法吗?
A
B
C
D
E
F
180° × 4 – 180° = 540°
探究3
返回
A
B
C
D
E
F
180°× 3– 180° = 360°
180°× 4 – 180° = 540°
180°× 5 – 180° = 720°
返回
n边形 : 180 ×(n-1)– 180°= (n-2) ·180
探究4
A
B
C
D
E
4 × 180°-180 °
O
=540°
返回
B
C
D
E
180°× 3– 180° = 360°
180°× 4 – 180° = 540°
180°× 5 – 180° = 720°
返回
n边形 : 180 ×(n-1)– 180°= (n-2) ·180
