2020-2021学年人教版八年级上册数学课堂小测 12.2三角形全等的判定(word版含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级上册数学课堂小测 12.2三角形全等的判定(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 263.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-28 00:00:00 | ||
图片预览

文档简介
2020-2021学年人教版八年级上册数学课堂小测
12.2三角形全等的判定
一,选择题
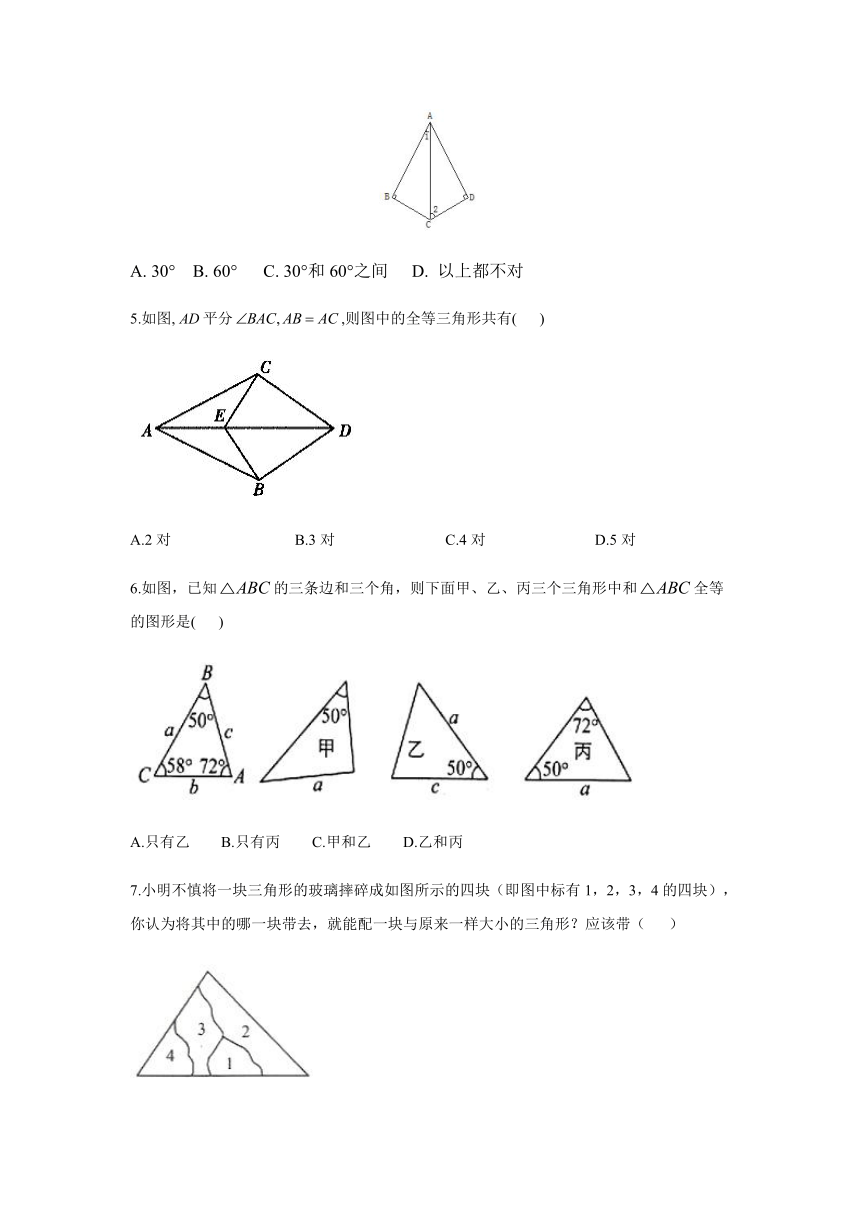
1.如图,中,,,则由“”可以判定( )
A.
B.
C.
D.以上答案都不对
2.
如图,AB=AC,AD=AE,欲证△ABD≌△ACE,可补充条件(
)
A.∠1=∠2
B.∠B=∠C
C.∠D=∠E
D.∠BAE=∠CAD
3.
如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
A.
AB=AC
B.
BD=CD
C.
∠B=∠C
D.∠BDA=∠CDA
4.
如图,∠B=∠D=90°,BC=CD,∠1=30°,则∠2的度数为(
)
A.
30°
B.
60°
C.
30°和60°之间
D.
以上都不对
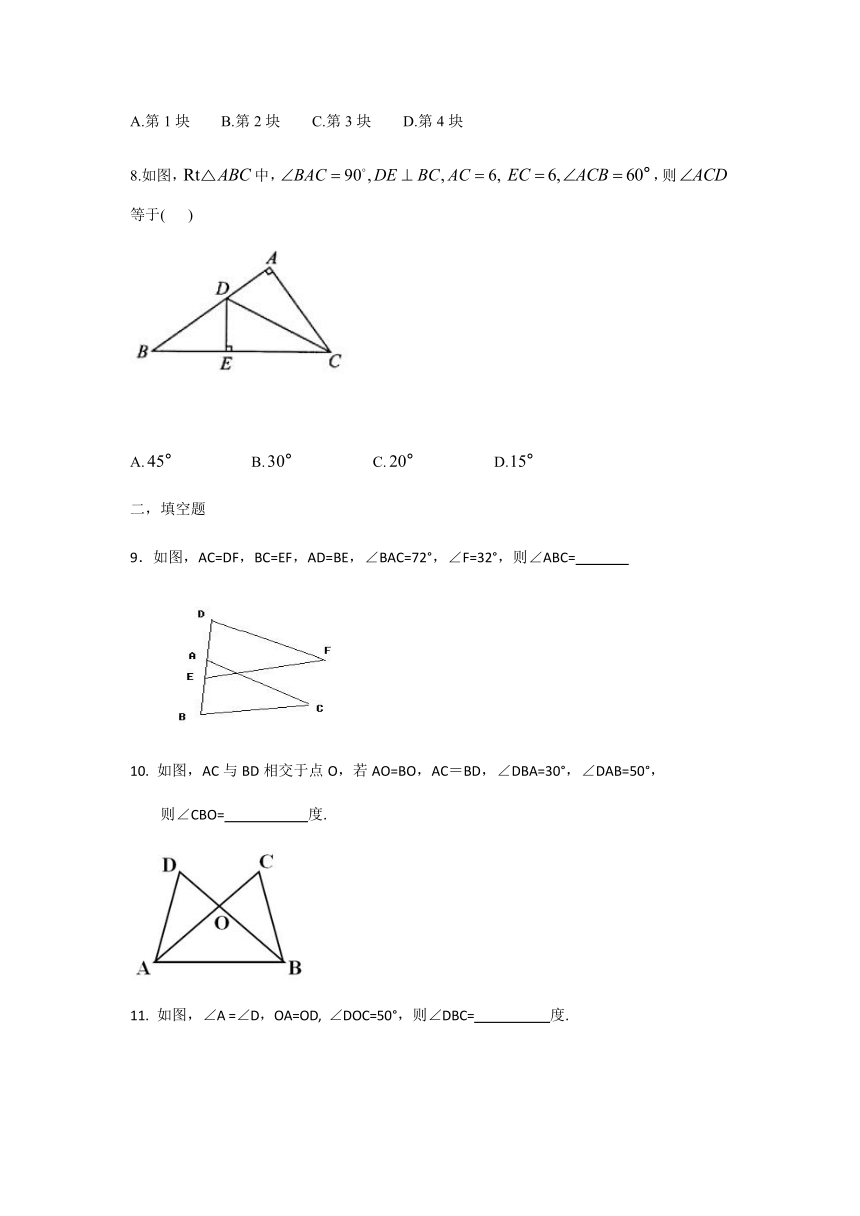
5.如图,平分,则图中的全等三角形共有(
)
A.2对
B.3对
C.4对
D.5对
6.如图,已知的三条边和三个角,则下面甲、乙、丙三个三角形中和全等的图形是(
)
A.只有乙
B.只有丙
C.甲和乙
D.乙和丙
7.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1,2,3,4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带(
)
A.第1块
B.第2块
C.第3块
D.第4块
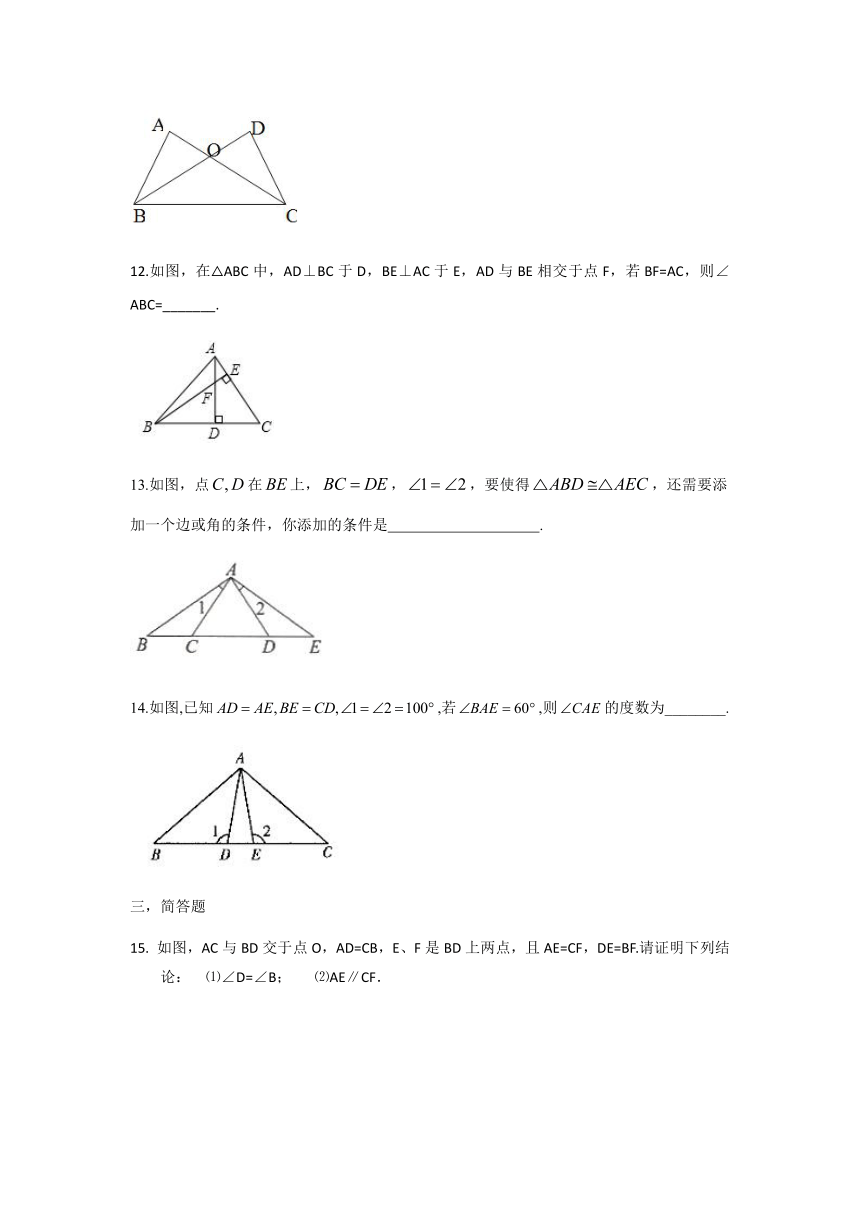
8.如图,中,,则等于(
)
A.
B.
C.
D.
二,填空题
9.如图,AC=DF,BC=EF,AD=BE,∠BAC=72°,∠F=32°,则∠ABC=
10.
如图,AC与BD相交于点O,若AO=BO,AC=BD,∠DBA=30°,∠DAB=50°,
则∠CBO=
度.
11.
如图,∠A
=∠D,OA=OD,
∠DOC=50°,则∠DBC=
度.
12.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC=_______.
13.如图,点在上,,,要使得,还需要添加一个边或角的条件,你添加的条件是
.
14.如图,已知,若,则的度数为________.
三,简答题
15.
如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请证明下列结论:
⑴∠D=∠B;
⑵AE∥CF.
16.
已知:如图,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.
求证:∠ACE=∠DBF.
17.
已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.求证:AB=DC
18.
如图
AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
19.如图,在四边形中,,延长到,使,连接.
(1)求证:.
(2)求证:.
答案以及解析
1.答案:B
2.答案:A
3.答案:B
4.答案:B
5.答案:B
解析:平分.在和中,.在和中,,.在和中,共有3对全等三角形.故选B.
6.答案:D
解析:甲三角形只知道一条边长、一个内角度救无法判断是否与全等;乙三角形夹内角的两边分别与已知三角形对应相等.故乙与全等;丙三角形内角及所对边与对应相等且均有内角,可根据AAS判定丙与全等.则与全等的有乙和丙.
7.答案:B
解析:第4块只保留了一个角及部分边,不能配成和原来一样大小的三角形玻璃;第1块和第3块则只保留了部分边,不能配成和原来一样大小的三角形玻璃;而第2块不但保留了一个完整的边还保留了两个角,所以应该带第2块去,根据“ASA”可知,可以配出一块和原来一样大小的三角形玻璃故选B
8.答案:B
解析:.又
.
9.答案:760
10.
答案:20
11.答案:
25
12.答案:45°
13.答案:
(答案不唯一)
解析:添加
(答案不唯一)
,,即
,,
即,
在和中,,.
14.答案:40°
解析:,.在和中,,.
15.
证明:(1)在△EAD和△FCB中
AD=CB,AE=CF,DE=BF
∴△EAD≌△FCB(SSS)
∴∠D=∠B
(2)由(1)知:△EAD≌△FCB
∴∠DEA=∠BFC
∵∠AEO=180-∠DEA,
∠CFO=180-∠BFC,
∴∠AEO=∠CFO
∴
AE∥CF
16.
证明:∵AB=DC
∴AC=DB
∵EA⊥AD,FD⊥AD
∴∠A=∠D=90°
在△EAC与△FDB中
∴△EAC≌△FDB
∴∠ACE=∠DBF.
17.
证明:在△ABC与△DCB中
∴△ABC≌△DCB
∴AB=DC
18.(1)证明:在△ACD与△ABE中,
∵∠A=∠A,∠ADC=∠AEB=90°,AB=AC,
∴△ACD≌△ABE,
∴AD=AE.
(2)互相垂直,
在Rt△ADO与△AEO中,
∵OA=OA,AD=AE,
∴△ADO≌△AEO,
∴∠DAO=∠EAO,
即OA是∠BAC的平分线,
又∵AB=AC,
∴OA⊥BC.
19.答案:(1)在四边形中,,
,
又.
(2)由(1)知.
在△ABC和△EDC中,
所以△ABC≌△EDC(SAS)
解析:
12.2三角形全等的判定
一,选择题
1.如图,中,,,则由“”可以判定( )
A.
B.
C.
D.以上答案都不对
2.
如图,AB=AC,AD=AE,欲证△ABD≌△ACE,可补充条件(
)
A.∠1=∠2
B.∠B=∠C
C.∠D=∠E
D.∠BAE=∠CAD
3.
如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
A.
AB=AC
B.
BD=CD
C.
∠B=∠C
D.∠BDA=∠CDA
4.
如图,∠B=∠D=90°,BC=CD,∠1=30°,则∠2的度数为(
)
A.
30°
B.
60°
C.
30°和60°之间
D.
以上都不对
5.如图,平分,则图中的全等三角形共有(
)
A.2对
B.3对
C.4对
D.5对
6.如图,已知的三条边和三个角,则下面甲、乙、丙三个三角形中和全等的图形是(
)
A.只有乙
B.只有丙
C.甲和乙
D.乙和丙
7.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1,2,3,4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带(
)
A.第1块
B.第2块
C.第3块
D.第4块
8.如图,中,,则等于(
)
A.
B.
C.
D.
二,填空题
9.如图,AC=DF,BC=EF,AD=BE,∠BAC=72°,∠F=32°,则∠ABC=
10.
如图,AC与BD相交于点O,若AO=BO,AC=BD,∠DBA=30°,∠DAB=50°,
则∠CBO=
度.
11.
如图,∠A
=∠D,OA=OD,
∠DOC=50°,则∠DBC=
度.
12.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC=_______.
13.如图,点在上,,,要使得,还需要添加一个边或角的条件,你添加的条件是
.
14.如图,已知,若,则的度数为________.
三,简答题
15.
如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请证明下列结论:
⑴∠D=∠B;
⑵AE∥CF.
16.
已知:如图,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.
求证:∠ACE=∠DBF.
17.
已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.求证:AB=DC
18.
如图
AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
19.如图,在四边形中,,延长到,使,连接.
(1)求证:.
(2)求证:.
答案以及解析
1.答案:B
2.答案:A
3.答案:B
4.答案:B
5.答案:B
解析:平分.在和中,.在和中,,.在和中,共有3对全等三角形.故选B.
6.答案:D
解析:甲三角形只知道一条边长、一个内角度救无法判断是否与全等;乙三角形夹内角的两边分别与已知三角形对应相等.故乙与全等;丙三角形内角及所对边与对应相等且均有内角,可根据AAS判定丙与全等.则与全等的有乙和丙.
7.答案:B
解析:第4块只保留了一个角及部分边,不能配成和原来一样大小的三角形玻璃;第1块和第3块则只保留了部分边,不能配成和原来一样大小的三角形玻璃;而第2块不但保留了一个完整的边还保留了两个角,所以应该带第2块去,根据“ASA”可知,可以配出一块和原来一样大小的三角形玻璃故选B
8.答案:B
解析:.又
.
9.答案:760
10.
答案:20
11.答案:
25
12.答案:45°
13.答案:
(答案不唯一)
解析:添加
(答案不唯一)
,,即
,,
即,
在和中,,.
14.答案:40°
解析:,.在和中,,.
15.
证明:(1)在△EAD和△FCB中
AD=CB,AE=CF,DE=BF
∴△EAD≌△FCB(SSS)
∴∠D=∠B
(2)由(1)知:△EAD≌△FCB
∴∠DEA=∠BFC
∵∠AEO=180-∠DEA,
∠CFO=180-∠BFC,
∴∠AEO=∠CFO
∴
AE∥CF
16.
证明:∵AB=DC
∴AC=DB
∵EA⊥AD,FD⊥AD
∴∠A=∠D=90°
在△EAC与△FDB中
∴△EAC≌△FDB
∴∠ACE=∠DBF.
17.
证明:在△ABC与△DCB中
∴△ABC≌△DCB
∴AB=DC
18.(1)证明:在△ACD与△ABE中,
∵∠A=∠A,∠ADC=∠AEB=90°,AB=AC,
∴△ACD≌△ABE,
∴AD=AE.
(2)互相垂直,
在Rt△ADO与△AEO中,
∵OA=OA,AD=AE,
∴△ADO≌△AEO,
∴∠DAO=∠EAO,
即OA是∠BAC的平分线,
又∵AB=AC,
∴OA⊥BC.
19.答案:(1)在四边形中,,
,
又.
(2)由(1)知.
在△ABC和△EDC中,
所以△ABC≌△EDC(SAS)
解析:
