鲁教版七年级上册期中数学测试题(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
鲁教版数学七年级上册期中测试题
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共36分)
1.下列图中不是轴对称图形的是( )
2.如图,A,B,C分别表示三个村庄,AB=1000 m,BC=600 m,AC=800 m,在抗击新型冠状肺炎疫情中,为了便于群众领取抗击疫情物资,拟建一个疫情物资中心,要求这三个村庄到物资中心的距离相等,则物资中心P的位置应在( )
A. AB的中点 B. BC的中点 C. AC的中点 D.∠C的平分线与AB的交点
第2题图 第3题图 第4题图
3.如图,已知∠1=∠2,AC=AD,从下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E中添加一个条件,能使△ABC≌△AED的有( )
A. 1个 B. 2个 C. 3个 D. 4个
4.如图,在△ABC中,AB=AC=BC,CD是∠ACB的平分线,过点D作DE∥BC交AC于点E.若△ABC的边长为a,则△ADE的周长是( )
A. 2a B. a C. a D. a
5.如果三角形的两边长分别为3和5,那么这个三角形的周长可能是( )
A. 9 B. 10 C. 15 D. 16
6.小明同学先向北行进4 km,然后向东行进4 km,再向北行进2 km,最后又向东行进一定距离,此时小明离出发点的距离是10 km,小明最后向东行进了( )
A. 3 km B. 4 km C. 5 km D. 6 km
7.如果等腰三角形的两边长分别是6 cm和3 cm,那么它的周长是( )
A. 9 cm B. 12 cm C. 15或12 cm D. 15 cm
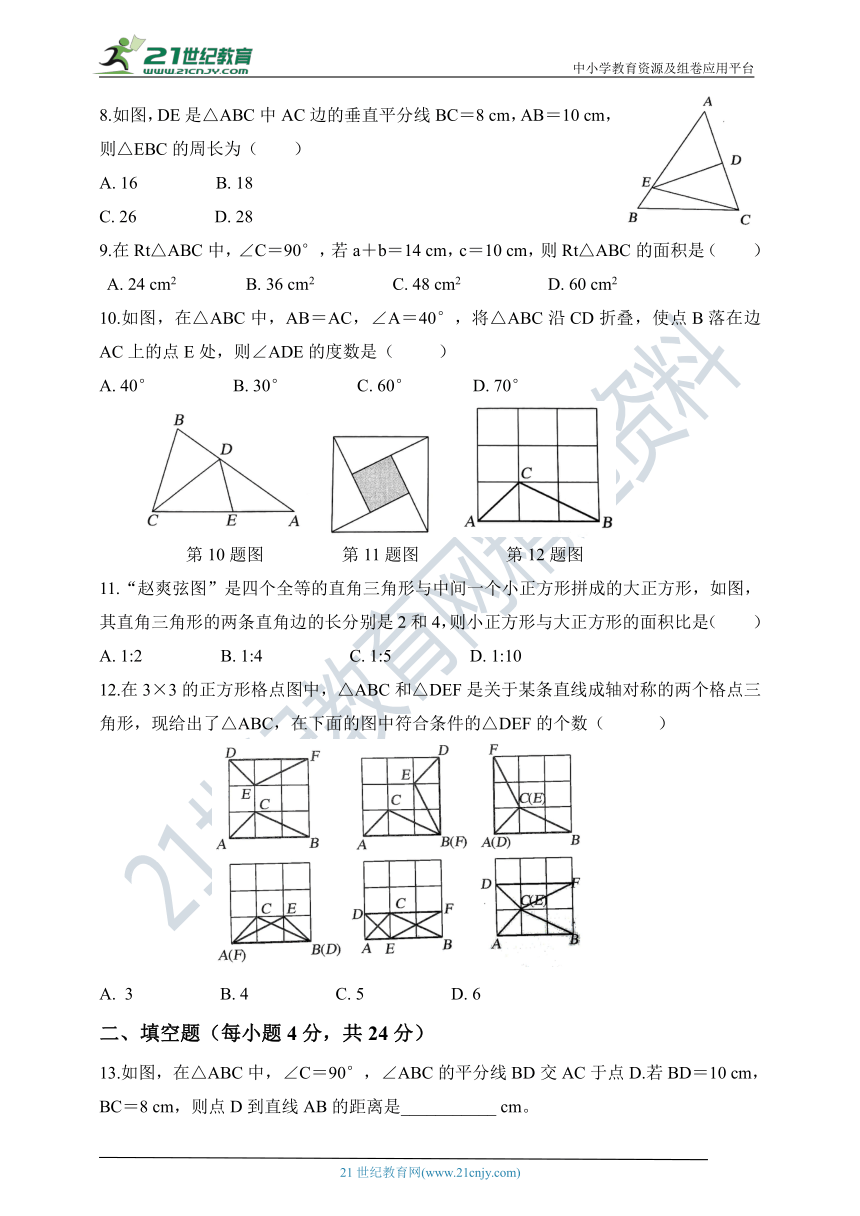
8.如图,DE是△ABC中AC边的垂直平分线BC=8 cm,AB=10 cm,则△EBC的周长为( )
A. 16 B. 18
C. 26 D. 28
9.在Rt△ABC中,∠C=90°,若a+b=14 cm,c=10 cm,则Rt△ABC的面积是( )
A. 24 cm2 B. 36 cm2 C. 48 cm2 D. 60 cm2
10.如图,在△ABC中,AB=AC,∠A=40°,将△ABC沿CD折叠,使点B落在边AC上的点E处,则∠ADE的度数是( )
A. 40° B. 30° C. 60° D. 70°
第10题图 第11题图 第12题图
11.“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形,如图,其直角三角形的两条直角边的长分别是2和4,则小正方形与大正方形的面积比是( )
A. 1:2 B. 1:4 C. 1:5 D. 1:10
12.在3×3的正方形格点图中,△ABC和△DEF是关于某条直线成轴对称的两个格点三角形,现给出了△ABC,在下面的图中符合条件的△DEF的个数( )
3 B. 4 C. 5 D. 6
二、填空题(每小题4分,共24分)
13.如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BD=10 cm,BC=8 cm,则点D到直线AB的距离是___________ cm。
第13题图 第15题图
14.在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=12 cm,那么斜边AB的长度为____________ cm.
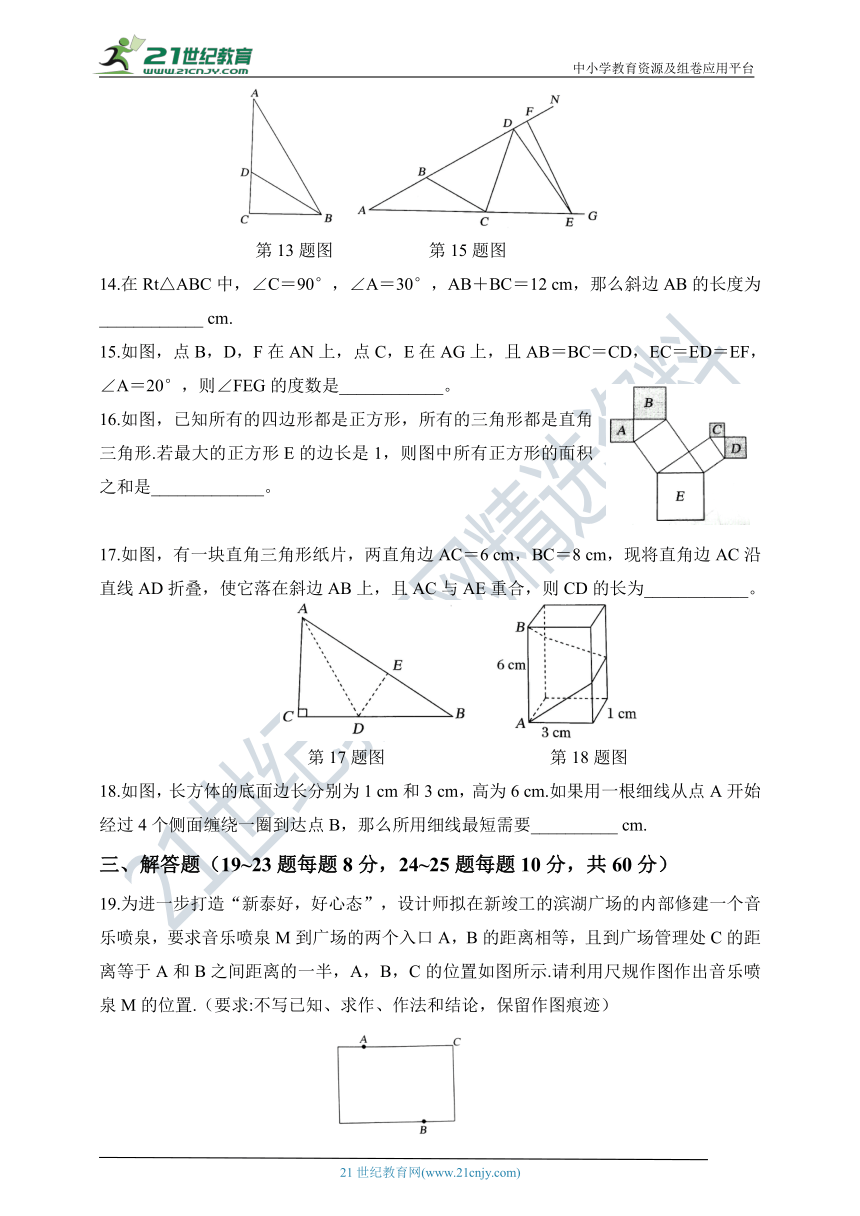
15.如图,点B,D,F在AN上,点C,E在AG上,且AB=BC=CD,EC=ED=EF,∠A=20°,则∠FEG的度数是____________。
16.如图,已知所有的四边形都是正方形,所有的三角形都是直角三角形.若最大的正方形E的边长是1,则图中所有正方形的面积之和是_____________。
17.如图,有一块直角三角形纸片,两直角边AC=6 cm,BC=8 cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且AC与AE重合,则CD的长为____________。
第17题图 第18题图
18.如图,长方体的底面边长分别为1 cm和3 cm,高为6 cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要__________ cm.
三、解答题(19~23题每题8分,24~25题每题10分,共60分)
19.为进一步打造“新泰好,好心态”,设计师拟在新竣工的滨湖广场的内部修建一个音乐喷泉,要求音乐喷泉M到广场的两个入口A,B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A,B,C的位置如图所示.请利用尺规作图作出音乐喷泉M的位置.(要求:不写已知、求作、作法和结论,保留作图痕迹)
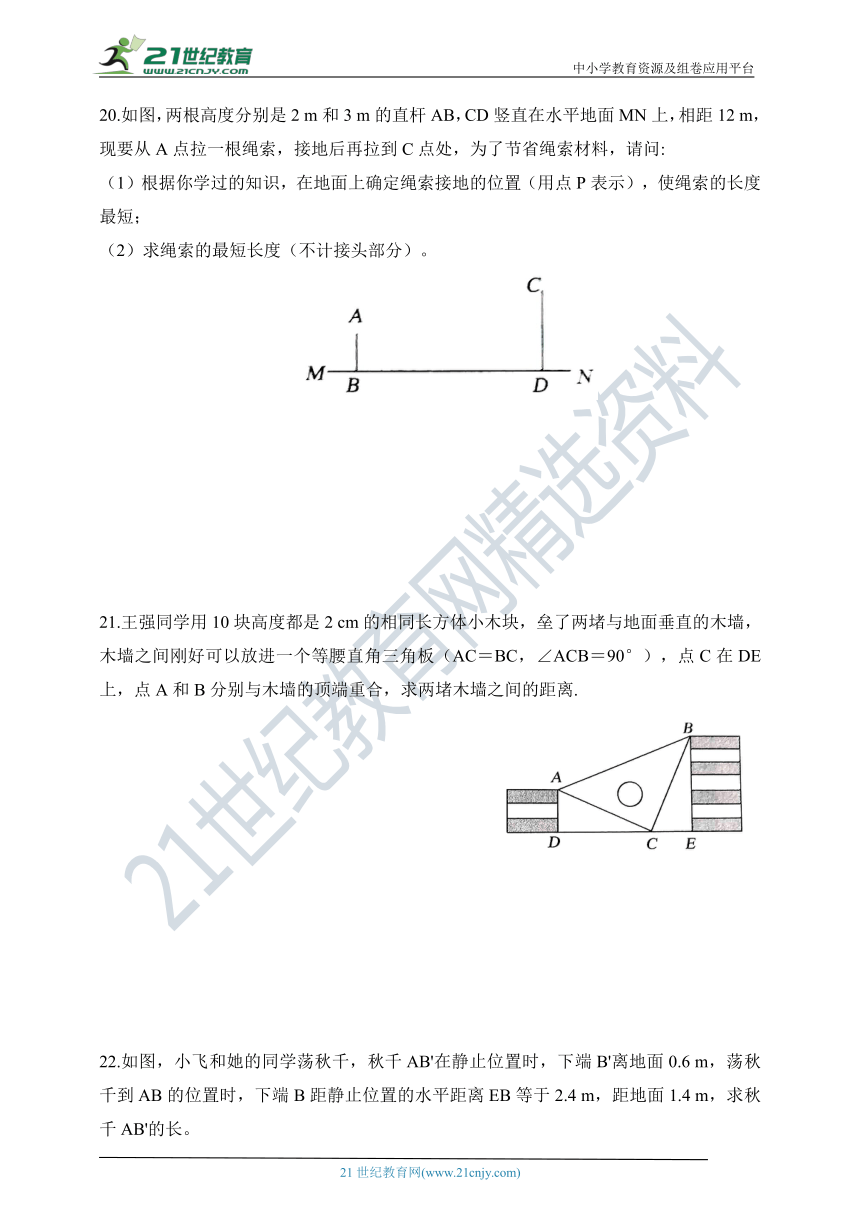
20.如图,两根高度分别是2 m和3 m的直杆AB,CD竖直在水平地面MN上,相距12 m,现要从A点拉一根绳索,接地后再拉到C点处,为了节省绳索材料,请问:
(1)根据你学过的知识,在地面上确定绳索接地的位置(用点P表示),使绳索的长度最短;
(2)求绳索的最短长度(不计接头部分)。
21.王强同学用10块高度都是2 cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离.
22.如图,小飞和她的同学荡秋千,秋千AB'在静止位置时,下端B'离地面0.6 m,荡秋千到AB的位置时,下端B距静止位置的水平距离EB等于2.4 m,距地面1.4 m,求秋千AB'的长。
23.如图,在△ABC中,AB=AC,∠BAC=36°,BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF。
求证:(1)EF⊥AB;
(2)△ACF为等腰三角形。
24.如图,在甲村至乙村间有一条公路,在C处需要爆破,已知点C与公路上的停靠站A的距离为300 m,与公路上的另一停靠站B的距离为400 m,且CA⊥CB为了安全起见,爆破点C周围半径250 m范围内不得进入,问在进行爆破时,公路AB段是否有危险?请用你学过的知识加以解答。
25.在△ABC中,∠BAC=90°,AC=AB,点D为直线BC上的一动点,以AD为边作△ADE(顶点A,DE按逆时针方向排列),且∠DAE=90°,AD=AE连接CE。
(1)如图1,若点D在BC边上(点D与B,C不重合),求∠BCE的度数;
(2)如图2,若点D在CB的延长线上,若DB=5,BC=7,求△ADE的面积。
参考答案
一、选择题
1. C 2. A 3. C 4. C 5. C 6. B 7. D 8. B
9. A 10. B 11. C 12. D
二、填空题
13. 6 14. 8 15. 100? 16. 3 17. 3 cm 18. 10
三、解答题
19.解:作AB的垂直平分线,以点C为圆心,以AB的一半为半径画弧交AB的垂直平分线于点M即可。
20.解:(1)如图1,作点A关于MN的对称点A′,连接A′C,交MN于点P.点P即为所求。
(2)如图2,作AE∥MN,交CD的延长线于点E.
由题意得AE=BD=12,DE=A′B=AB=2,
∠A′EC=90°。因为CD=3,所以CE=CD+DE=5。
在Rt△A′EC中,由勾股定理,得A′C==13(m).
由轴对称的性质得PA=PA′。所以PA+PC=PA′+PC=A′C=13(m)。
答:绳索的最短长度为13 m。
21.解:由题意得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
所以∠ADC=∠CEB=90°。所以∠ACD+∠BCE=90°,∠ACD+∠DAC=90°。
所以∠BCE=∠DAC。
在△ADC和△CEB中,因为所以△ADC≌△CEB(AAS).
所以AD=CE=6 cm,DC=EB=14 cm.所以DE=DC+CE=20(cm)
答:两堵木墙之间的距离为20 cm.
22.解:设AB=x m,则AB′=x m.
由题意可得B′E=1.4-0.6=0.8(m)则AE=AB′-0.8.
在Rt△AEB中,AE2+BE2=AB2,则(x-0.8)2+2.42=x2,解得x=4。
答:秋千AB′的长为4 m.
23.证明:(1)因为AB=AC,∠BAC=36°,所以∠ABC=∠ACB=72°。
又因为BD是∠ABC的平分线,所以∠ABD=36°。
所以∠BAD=∠ABD。所以AD=BD.
又因为E是AB的中点,所以DE⊥AB,即EF⊥AB.
(2)因为EF⊥AB,AE=BE,所以EF垂直平分AB.所以AF=BF.
所以∠BAF=∠ABF.又因为∠BAD=∠ABD,所以∠FAD=∠FBD=36°。
又因为∠ACB=72°,所以∠AFC=∠ACB-∠CAF=36°。
所以∠CAF=∠AFC=36°,所以AC=CF,即△ACF为等腰三角形。
24.解:公路AB有危险.理由如下:
如图,过点C作CD⊥AB于点D.
因为BC=400 m,AC=300 m,∠ACB=90°,所以根据勾股定理可得AB=500 m.
因为S△ABC=AB·CD=BC·AC.
所以CD===240(m)。由于240m<250m,故有危险.
25.解:(1)如图1,因为∠BAC=90°,∠DAE=90°,
所以∠BAD+∠DAC=90°,∠EAC+∠DAC=90°。所以∠BAD=∠EAC.
在△ABD和△ACE中,因为所以△ABD≌△ACE(SAS).
所以∠B=∠ACE.因为∠BAC=90°。所以∠B+∠ACB=90°。
所以∠ACE+∠ACB=90°,即∠BCE=90°。
(2)如图2,过点A作AF⊥DE于点F。
因为AD=AE,所以点F是DE的中点.
因为∠DAE=90°所以AF=DE.
同(1)可证:△ABD≌△ACE.
所以BD=CE=5,∠ABD=∠ACE=180°-∠ABC=135°。
因为∠BAC=90°,AC=AB,所以∠ACB=45°。
所以∠DCE=∠ACE-∠ACB=90°。又因为DC=BD+BC=5+7=12,
所以DE==13.所以AF=。
所以△ADE的面积为DE·AF=×13×=。
_21?????????è?????(www.21cnjy.com)_
鲁教版数学七年级上册期中测试题
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共36分)
1.下列图中不是轴对称图形的是( )
2.如图,A,B,C分别表示三个村庄,AB=1000 m,BC=600 m,AC=800 m,在抗击新型冠状肺炎疫情中,为了便于群众领取抗击疫情物资,拟建一个疫情物资中心,要求这三个村庄到物资中心的距离相等,则物资中心P的位置应在( )
A. AB的中点 B. BC的中点 C. AC的中点 D.∠C的平分线与AB的交点
第2题图 第3题图 第4题图
3.如图,已知∠1=∠2,AC=AD,从下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E中添加一个条件,能使△ABC≌△AED的有( )
A. 1个 B. 2个 C. 3个 D. 4个
4.如图,在△ABC中,AB=AC=BC,CD是∠ACB的平分线,过点D作DE∥BC交AC于点E.若△ABC的边长为a,则△ADE的周长是( )
A. 2a B. a C. a D. a
5.如果三角形的两边长分别为3和5,那么这个三角形的周长可能是( )
A. 9 B. 10 C. 15 D. 16
6.小明同学先向北行进4 km,然后向东行进4 km,再向北行进2 km,最后又向东行进一定距离,此时小明离出发点的距离是10 km,小明最后向东行进了( )
A. 3 km B. 4 km C. 5 km D. 6 km
7.如果等腰三角形的两边长分别是6 cm和3 cm,那么它的周长是( )
A. 9 cm B. 12 cm C. 15或12 cm D. 15 cm
8.如图,DE是△ABC中AC边的垂直平分线BC=8 cm,AB=10 cm,则△EBC的周长为( )
A. 16 B. 18
C. 26 D. 28
9.在Rt△ABC中,∠C=90°,若a+b=14 cm,c=10 cm,则Rt△ABC的面积是( )
A. 24 cm2 B. 36 cm2 C. 48 cm2 D. 60 cm2
10.如图,在△ABC中,AB=AC,∠A=40°,将△ABC沿CD折叠,使点B落在边AC上的点E处,则∠ADE的度数是( )
A. 40° B. 30° C. 60° D. 70°
第10题图 第11题图 第12题图
11.“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形,如图,其直角三角形的两条直角边的长分别是2和4,则小正方形与大正方形的面积比是( )
A. 1:2 B. 1:4 C. 1:5 D. 1:10
12.在3×3的正方形格点图中,△ABC和△DEF是关于某条直线成轴对称的两个格点三角形,现给出了△ABC,在下面的图中符合条件的△DEF的个数( )
3 B. 4 C. 5 D. 6
二、填空题(每小题4分,共24分)
13.如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BD=10 cm,BC=8 cm,则点D到直线AB的距离是___________ cm。
第13题图 第15题图
14.在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=12 cm,那么斜边AB的长度为____________ cm.
15.如图,点B,D,F在AN上,点C,E在AG上,且AB=BC=CD,EC=ED=EF,∠A=20°,则∠FEG的度数是____________。
16.如图,已知所有的四边形都是正方形,所有的三角形都是直角三角形.若最大的正方形E的边长是1,则图中所有正方形的面积之和是_____________。
17.如图,有一块直角三角形纸片,两直角边AC=6 cm,BC=8 cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且AC与AE重合,则CD的长为____________。
第17题图 第18题图
18.如图,长方体的底面边长分别为1 cm和3 cm,高为6 cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要__________ cm.
三、解答题(19~23题每题8分,24~25题每题10分,共60分)
19.为进一步打造“新泰好,好心态”,设计师拟在新竣工的滨湖广场的内部修建一个音乐喷泉,要求音乐喷泉M到广场的两个入口A,B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A,B,C的位置如图所示.请利用尺规作图作出音乐喷泉M的位置.(要求:不写已知、求作、作法和结论,保留作图痕迹)
20.如图,两根高度分别是2 m和3 m的直杆AB,CD竖直在水平地面MN上,相距12 m,现要从A点拉一根绳索,接地后再拉到C点处,为了节省绳索材料,请问:
(1)根据你学过的知识,在地面上确定绳索接地的位置(用点P表示),使绳索的长度最短;
(2)求绳索的最短长度(不计接头部分)。
21.王强同学用10块高度都是2 cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离.
22.如图,小飞和她的同学荡秋千,秋千AB'在静止位置时,下端B'离地面0.6 m,荡秋千到AB的位置时,下端B距静止位置的水平距离EB等于2.4 m,距地面1.4 m,求秋千AB'的长。
23.如图,在△ABC中,AB=AC,∠BAC=36°,BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF。
求证:(1)EF⊥AB;
(2)△ACF为等腰三角形。
24.如图,在甲村至乙村间有一条公路,在C处需要爆破,已知点C与公路上的停靠站A的距离为300 m,与公路上的另一停靠站B的距离为400 m,且CA⊥CB为了安全起见,爆破点C周围半径250 m范围内不得进入,问在进行爆破时,公路AB段是否有危险?请用你学过的知识加以解答。
25.在△ABC中,∠BAC=90°,AC=AB,点D为直线BC上的一动点,以AD为边作△ADE(顶点A,DE按逆时针方向排列),且∠DAE=90°,AD=AE连接CE。
(1)如图1,若点D在BC边上(点D与B,C不重合),求∠BCE的度数;
(2)如图2,若点D在CB的延长线上,若DB=5,BC=7,求△ADE的面积。
参考答案
一、选择题
1. C 2. A 3. C 4. C 5. C 6. B 7. D 8. B
9. A 10. B 11. C 12. D
二、填空题
13. 6 14. 8 15. 100? 16. 3 17. 3 cm 18. 10
三、解答题
19.解:作AB的垂直平分线,以点C为圆心,以AB的一半为半径画弧交AB的垂直平分线于点M即可。
20.解:(1)如图1,作点A关于MN的对称点A′,连接A′C,交MN于点P.点P即为所求。
(2)如图2,作AE∥MN,交CD的延长线于点E.
由题意得AE=BD=12,DE=A′B=AB=2,
∠A′EC=90°。因为CD=3,所以CE=CD+DE=5。
在Rt△A′EC中,由勾股定理,得A′C==13(m).
由轴对称的性质得PA=PA′。所以PA+PC=PA′+PC=A′C=13(m)。
答:绳索的最短长度为13 m。
21.解:由题意得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
所以∠ADC=∠CEB=90°。所以∠ACD+∠BCE=90°,∠ACD+∠DAC=90°。
所以∠BCE=∠DAC。
在△ADC和△CEB中,因为所以△ADC≌△CEB(AAS).
所以AD=CE=6 cm,DC=EB=14 cm.所以DE=DC+CE=20(cm)
答:两堵木墙之间的距离为20 cm.
22.解:设AB=x m,则AB′=x m.
由题意可得B′E=1.4-0.6=0.8(m)则AE=AB′-0.8.
在Rt△AEB中,AE2+BE2=AB2,则(x-0.8)2+2.42=x2,解得x=4。
答:秋千AB′的长为4 m.
23.证明:(1)因为AB=AC,∠BAC=36°,所以∠ABC=∠ACB=72°。
又因为BD是∠ABC的平分线,所以∠ABD=36°。
所以∠BAD=∠ABD。所以AD=BD.
又因为E是AB的中点,所以DE⊥AB,即EF⊥AB.
(2)因为EF⊥AB,AE=BE,所以EF垂直平分AB.所以AF=BF.
所以∠BAF=∠ABF.又因为∠BAD=∠ABD,所以∠FAD=∠FBD=36°。
又因为∠ACB=72°,所以∠AFC=∠ACB-∠CAF=36°。
所以∠CAF=∠AFC=36°,所以AC=CF,即△ACF为等腰三角形。
24.解:公路AB有危险.理由如下:
如图,过点C作CD⊥AB于点D.
因为BC=400 m,AC=300 m,∠ACB=90°,所以根据勾股定理可得AB=500 m.
因为S△ABC=AB·CD=BC·AC.
所以CD===240(m)。由于240m<250m,故有危险.
25.解:(1)如图1,因为∠BAC=90°,∠DAE=90°,
所以∠BAD+∠DAC=90°,∠EAC+∠DAC=90°。所以∠BAD=∠EAC.
在△ABD和△ACE中,因为所以△ABD≌△ACE(SAS).
所以∠B=∠ACE.因为∠BAC=90°。所以∠B+∠ACB=90°。
所以∠ACE+∠ACB=90°,即∠BCE=90°。
(2)如图2,过点A作AF⊥DE于点F。
因为AD=AE,所以点F是DE的中点.
因为∠DAE=90°所以AF=DE.
同(1)可证:△ABD≌△ACE.
所以BD=CE=5,∠ABD=∠ACE=180°-∠ABC=135°。
因为∠BAC=90°,AC=AB,所以∠ACB=45°。
所以∠DCE=∠ACE-∠ACB=90°。又因为DC=BD+BC=5+7=12,
所以DE==13.所以AF=。
所以△ADE的面积为DE·AF=×13×=。
_21?????????è?????(www.21cnjy.com)_
同课章节目录
