人教版 五年级数学上册12讲基本图形面积学案
文档属性
| 名称 | 人教版 五年级数学上册12讲基本图形面积学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-29 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
12讲 基本图形面积
一、平行四边形的面积
【知识梳理】
1.等底等高的平行四边形面积相等。
2.(1)已知平行四边形的面积,和高,则平行四边形的底边;
(2)已知平行四边形的面积,和底边,则平行四边形的高。
3.平行四边形的面积=底×高。
如果用表示平行四边形的面积,用表示平行四边形的底,用表示平行四边形的高,那么平行四边形的面积计算公式可以写成:。
【说明】
(1)在同一个平行四边形中,不同的底与它对应的高的乘积相等,都等于这个平行四边形的面积;
(2)平行四边形的面积与它的底和高有关,底扩大到原来的倍(),高缩小到原来的,面积不变。
【注意】求平行四边形的面积,先要找到一组相对应的底和高,再计算。
4.平行四边形面积公式推导:
(1)方法一:沿着平行四边形地边上的高把平行四边形剪成一个直角三角形和一个直角梯形→把直角三角形向右平移后拼在直角梯形的右边→使平行四边形转化成长方形;
(2)方法二:用剪刀将平行四边形沿一条高剪开,剪成两个直角梯形,把左边的直角梯形向右平移后拼在另一个直角梯形的右边,使平行四边形转化成长方形。
长方形的长平行四边形的底;
长方形的宽平行四边形的高;
平行四边形的面积=长方形的面积=长×高=底×高。
【例题精讲】
例1.已知平行四边形的面积是300平方分米,如果它的底缩小到原来的一,高扩大到原来的5倍,那么面积为( )。
A. 50平方分米; B. 60平方分米; C. 360平方分米; D. 250平方分米.
例2.平行四边形的底扩大到原来的3倍,高不变,面积就( )
A. 不变; B. 扩大到原来的3倍; C. 扩大到原来的6倍. D. 略
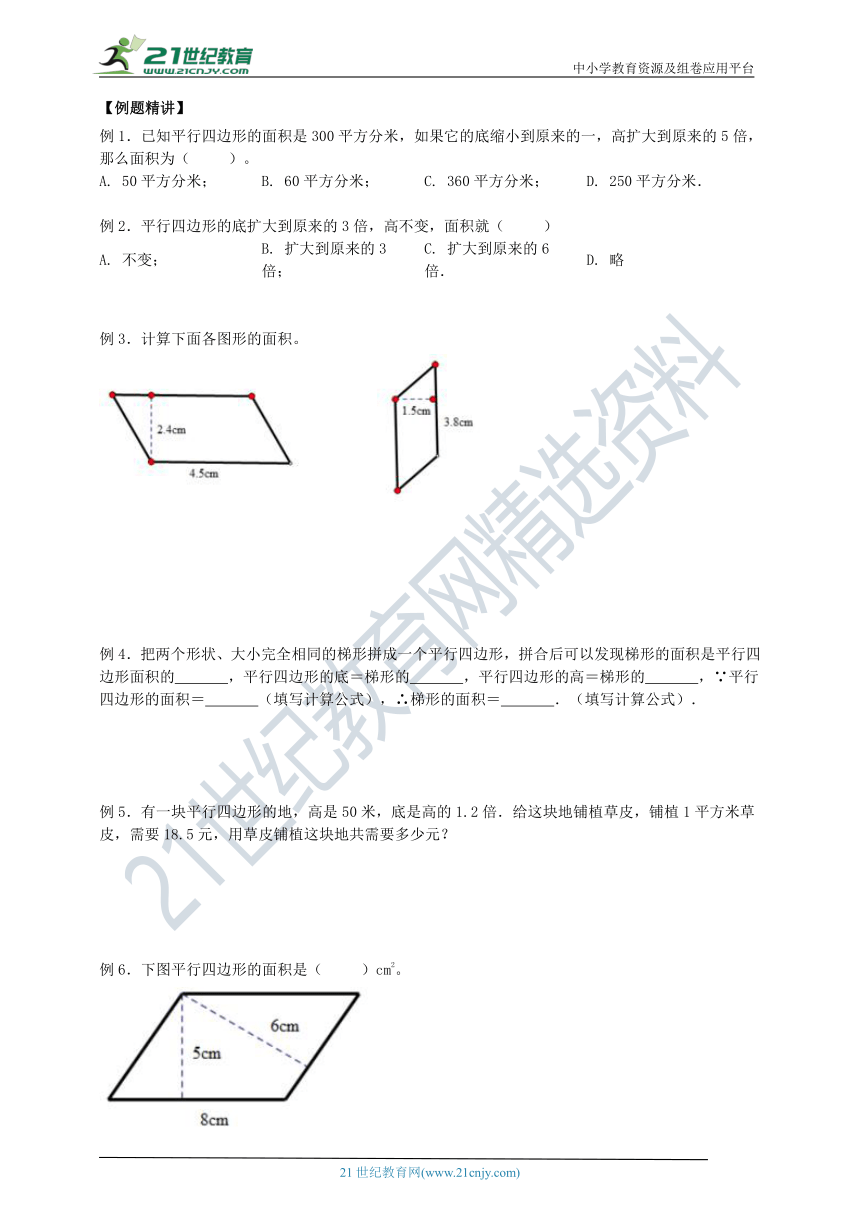
例3.计算下面各图形的面积。
例4.把两个形状、大小完全相同的梯形拼成一个平行四边形,拼合后可以发现梯形的面积是平行四边形面积的 ,平行四边形的底=梯形的 ,平行四边形的高=梯形的 ,∵平行四边形的面积= (填写计算公式),∴梯形的面积= .(填写计算公式).
例5.有一块平行四边形的地,高是50米,底是高的1.2倍.给这块地铺植草皮,铺植1平方米草皮,需要18.5元,用草皮铺植这块地共需要多少元?
例6.下图平行四边形的面积是( )cm2。
A. 40; B. 48; C. 30.
【巩固练习】
1.如图,已知长方形的面积是 78,宽是6,长6,那么平行四边形的面积
.
2.如下图,正方形的周长是28,①的面积是15,求阴影部分的面积。
3.填一填。
(1)把一个平行四边形沿( )剪开,可以将它拼成一个( )形。转化后图形的( )和( )相当于平行四边形的( )和( ),转化前后图形的( )是不变的。因此,平行四边形的面积等于( )
(2)计算表中平行四边形的面积。
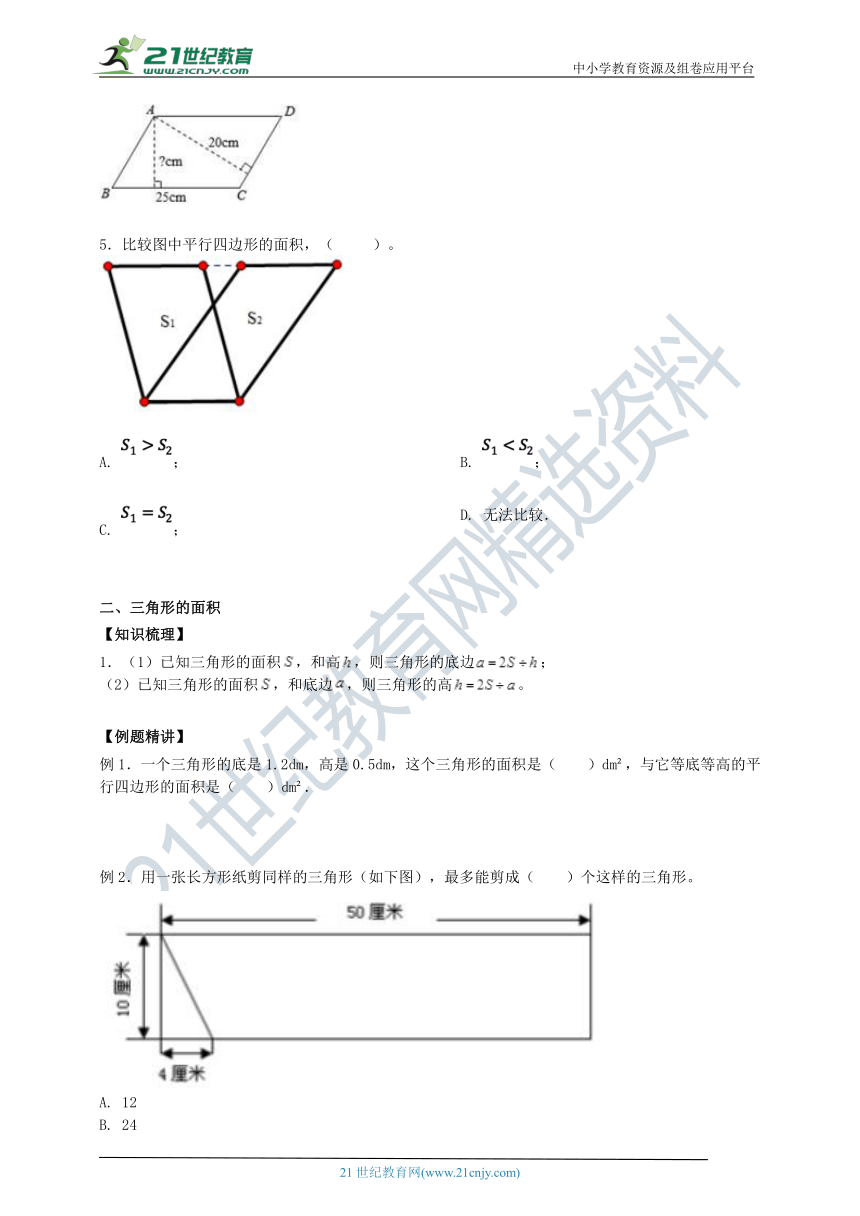
4. 一个平行四边形的周长是86(如图),以为底边时,对应的高是20,BC长为25,BC边上的高是多少厘米?
5.比较图中平行四边形的面积,( )。
A. ; B. ;
C. ; D. 无法比较.
二、三角形的面积
【知识梳理】
1.(1)已知三角形的面积,和高,则三角形的底边;
(2)已知三角形的面积,和底边,则三角形的高。
【例题精讲】
例1.一个三角形的底是1.2dm,高是0.5dm,这个三角形的面积是( )dm ,与它等底等高的平行四边形的面积是( )dm .
例2.用一张长方形纸剪同样的三角形(如下图),最多能剪成( )个这样的三角形。
A. 12
B. 24
C. 25
D. 10
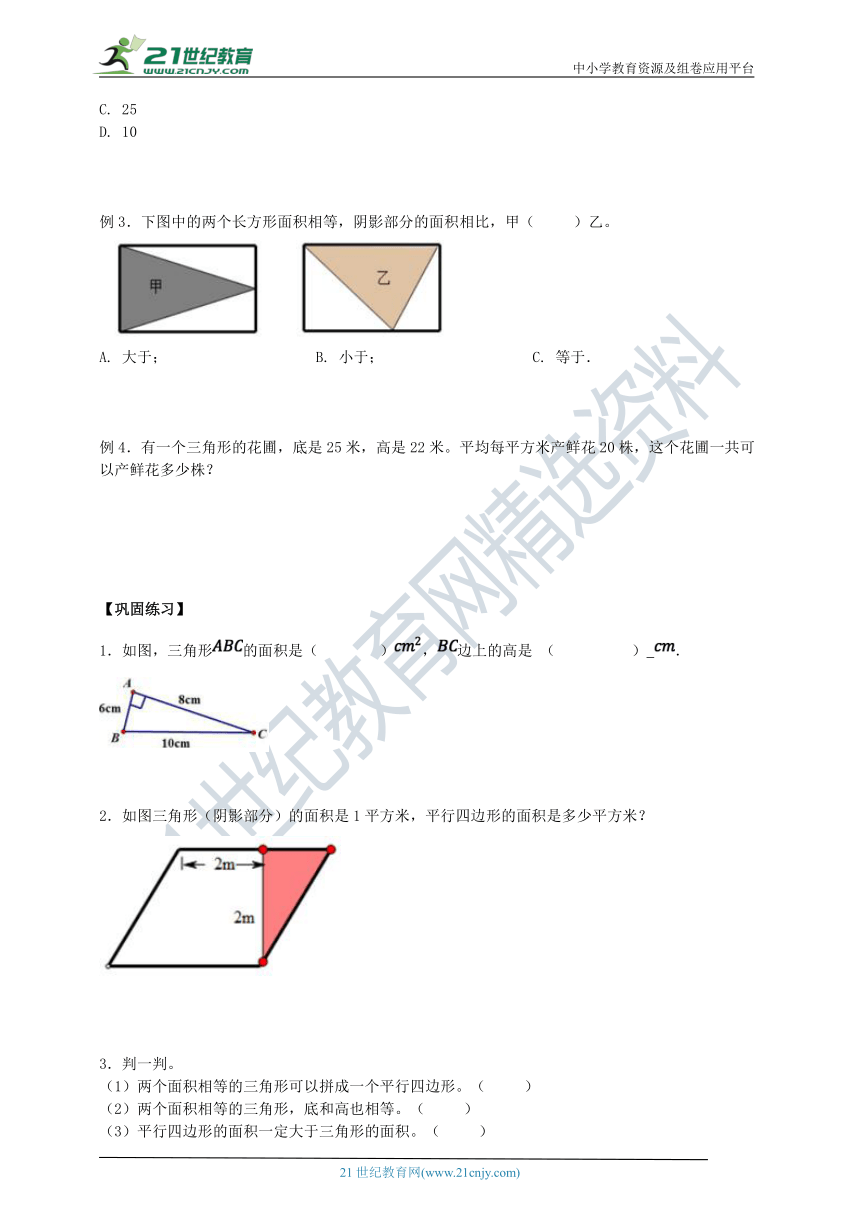
例3.下图中的两个长方形面积相等,阴影部分的面积相比,甲( )乙。
A. 大于; B. 小于; C. 等于.
例4.有一个三角形的花圃,底是25米,高是22米。平均每平方米产鲜花20株,这个花圃一共可以产鲜花多少株?
【巩固练习】
1.如图,三角形的面积是( ),边上的高是 ( ) .
2.如图三角形(阴影部分)的面积是1平方米,平行四边形的面积是多少平方米?
3.判一判。
(1)两个面积相等的三角形可以拼成一个平行四边形。( )
(2)两个面积相等的三角形,底和高也相等。( )
(3)平行四边形的面积一定大于三角形的面积。( )
(4)等底等高的两个三角形面积相等。( )
(5)一个三角形和一个平行四边形面积相等,底也相等,三角形的高是4厘米,则平行四边形的高是2厘米。( )
4.如图,两条平行线间的3个三角形的面积关系是( )。
A. 不相等; B. 相等; C. 无法确定.
5. 一块三角形菜地,他的底是50m,高是30m,如果每平方米可种大白菜8棵,那么这块地一共可以种多少棵大白菜?如果平均每棵大白菜卖2元钱,那么这块地共收入多少元?
三、梯形的面积
【知识梳理】
1.梯形面积公式推导:
(1)方法一:运用拼摆法将两个完全一样的梯形拼成一个平行四边形。
将两个完全一样的梯形重叠在一起,一个梯形保持不动,另一个梯形绕任意一个顶点旋转180°,再平移,使两腰重合,即可拼成一个平行四边形。
平行四边形的底梯形的上底+下底;
平行四边形的高梯形的高;
梯形的面积=平行四边形的面积÷2=底×高÷2=(上底+下底)×高÷2。
(2)方法二:运用分割法把一个梯形分成两个三角形。
画出梯形的一条对角线,得到三角形①和三角形②,作出梯形的高。
梯形的面积=三角形①的面积+三角形②的面积=上底×高÷2+下底×高÷2。
【例题精讲】
例1.一个三角形与一个梯形的面积相等,高也相等,梯形的上底是3,下底是5,那么三角形的底是( ).
A. 5; B. 8; C. 10; D. 16.
例2.填一填。
(1)梯形的上底是10厘米,下底和高相等,都是12厘米,它的面积是( )平方厘米。
(2)一个直角梯形上底是18厘米,如果下底,缩短4厘米,原来的梯形就变成了正方形,原来梯形的面积是( )平方厘米。
例3.一个梯形的下底是上底的3倍,如果把上底延长8厘米,就得到一个平行四边形,且面积增加24平方厘米。这个梯形面积是多少平方厘米?
例4.填表。
【巩固练习】
1.用48米长的篱笆,在靠墙的地方围一块菜地(如右下图)。这块菜地的面积是多少平
方米?如果按照每平方米菜地一年能收入16.5元计算,这块菜地一年能收人多少元?
2.一个梯形的上底是4cm,下底是6cm,高是3cm.沿直线只剪一刀,剪出一个最大的平行四边形,这个平行四边形的面积是( ).
A. 9; B. 12; C. 16.
3.求下面各梯形的面积。(单位:分米)
4.比较图中两个阴影部分的面积,( )。
A. 甲=乙; B. 甲>乙; C. 甲<乙; D. 无法比较.
5.一个梯形的上底是,下底是10,高是8,它的面积是 ,当 时,它就是一个平行四边形.
【课堂检测】
1.如图所示,求梯形的面积。
2.汽车的前挡风玻璃是一个近似的梯形,上底为100,下底为132,高为55,如果这种玻璃的价格是每平方米660元,那么这块挡风玻璃的价钱是多少?
3.比较平行线间的两个阴影部分面积(如下图),( )。
A. 甲>乙; B. 甲<乙; C. 甲=乙; D. 无法比较.
4.如图是一块长方形草坪,长16米,宽10米,中间有两条路,一条是平行四边形,一条是长方形。求草坪的面积。
5.一个三角形和一个平行四边形的面积相等,高也相等,如果三角形的底是18cm,那么平行四边形的底是 .
6. 求图中阴影部分的面积。
7. 三角形的底是,如果底边延长,面积就增加,原三角形的面积是多少平方米?
8.如图,一个平行四边形和一个三角形拼成一个梯形,若梯形的面积是30cm2,则三角形的面积是 cm2.
参考答案
一、平行四边形的面积
【知识梳理】
1.等底等高的平行四边形面积相等。
2.(1)已知平行四边形的面积,和高,则平行四边形的底边;
(2)已知平行四边形的面积,和底边,则平行四边形的高。
3.平行四边形的面积=底×高。
如果用表示平行四边形的面积,用表示平行四边形的底,用表示平行四边形的高,那么平行四边形的面积计算公式可以写成:。
【说明】
(1)在同一个平行四边形中,不同的底与它对应的高的乘积相等,都等于这个平行四边形的面积;
(2)平行四边形的面积与它的底和高有关,底扩大到原来的倍(),高缩小到原来的,面积不变。
【注意】求平行四边形的面积,先要找到一组相对应的底和高,再计算。
4.平行四边形面积公式推导:
(1)方法一:沿着平行四边形地边上的高把平行四边形剪成一个直角三角形和一个直角梯形→把直角三角形向右平移后拼在直角梯形的右边→使平行四边形转化成长方形;
(2)方法二:用剪刀将平行四边形沿一条高剪开,剪成两个直角梯形,把左边的直角梯形向右平移后拼在另一个直角梯形的右边,使平行四边形转化成长方形。
长方形的长平行四边形的底;
长方形的宽平行四边形的高;
平行四边形的面积=长方形的面积=长×高=底×高。
【例题精讲】
例1.已知平行四边形的面积是300平方分米,如果它的底缩小到原来的一,高扩大到原来的5倍,那么面积为( )。
A. 50平方分米; B. 60平方分米; C. 360平方分米; D. 250平方分米.
【答案】D
例2.平行四边形的底扩大到原来的3倍,高不变,面积就( )
A. 不变; B. 扩大到原来的3倍; C. 扩大到原来的6倍. D. 略
【答案】B.
例3.计算下面各图形的面积。
【解答】4.5×2.4=10.8(cm2),3.8×1.5=5.7(cm2)。
【答案】10.8(cm2),5.7(cm2)
例4.把两个形状、大小完全相同的梯形拼成一个平行四边形,拼合后可以发现梯形的面积是平行四边形面积的 ,平行四边形的底=梯形的 ,平行四边形的高=梯形的 ,∵平行四边形的面积= (填写计算公式),∴梯形的面积= .(填写计算公式).
【答案】一半,上底与下底之和,高,底×高,(上底+下底)×高÷2.
例5.有一块平行四边形的地,高是50米,底是高的1.2倍.给这块地铺植草皮,铺植1平方米草皮,需要18.5元,用草皮铺植这块地共需要多少元?
【解答】解:底:50×1.2=60(米),
60×50×18.5=55500(元),
答:用草皮铺植这块地共需要55500元.
【答案】55500元.
例6.下图平行四边形的面积是( )cm2。
A. 40; B. 48; C. 30.
【答案】A
【巩固练习】
1.如图,已知长方形的面积是 78,宽是6,长6,那么平行四边形的面积
.
【答案】42.
2.如下图,正方形的周长是28,①的面积是15,求阴影部分的面积。
【答案】 28÷4=7() 7×7=49() 49-15=34()
3.填一填。
(1)把一个平行四边形沿( )剪开,可以将它拼成一个( )形。转化后图形的( )和( )相当于平行四边形的( )和( ),转化前后图形的( )是不变的。因此,平行四边形的面积等于( )
(2)计算表中平行四边形的面积。
【答案】(1)高,长方,长,宽,底,高,面积,底×高;(2)336,20.65,0.3。
4. 一个平行四边形的周长是86(如图),以为底边时,对应的高是20,BC长为25,BC边上的高是多少厘米?
【答案】 86÷2-25=18() 18×20÷25=14.4()
5.比较图中平行四边形的面积,( )。
A. ; B. ;
C. ; D. 无法比较.
【答案】C
二、三角形的面积
【知识梳理】
1.(1)已知三角形的面积,和高,则三角形的底边;
(2)已知三角形的面积,和底边,则三角形的高。
【例题精讲】
例1.一个三角形的底是1.2dm,高是0.5dm,这个三角形的面积是( )dm ,与它等底等高的平行四边形的面积是( )dm .
【答案】0.3,0.6
例2.用一张长方形纸剪同样的三角形(如下图),最多能剪成( )个这样的三角形。
A. 12
B. 24
C. 25
D. 10
【答案】B
例3.下图中的两个长方形面积相等,阴影部分的面积相比,甲( )乙。
A. 大于; B. 小于; C. 等于.
【答案】C
例4.有一个三角形的花圃,底是25米,高是22米。平均每平方米产鲜花20株,这个花圃一共可以产鲜花多少株?
【解答】25×22÷2×20=5500(株)
【答案】5500株
【巩固练习】
1.如图,三角形的面积是( ),边上的高是 ( ) .
【答案】24,4.8.
2.如图三角形(阴影部分)的面积是1平方米,平行四边形的面积是多少平方米?
【解答】1×2÷2=1(米),(2+1)×2=6(平方米)。
【答案】6平方米
3.判一判。
(1)两个面积相等的三角形可以拼成一个平行四边形。( )
(2)两个面积相等的三角形,底和高也相等。( )
(3)平行四边形的面积一定大于三角形的面积。( )
(4)等底等高的两个三角形面积相等。( )
(5)一个三角形和一个平行四边形面积相等,底也相等,三角形的高是4厘米,则平行四边形的高是2厘米。( )
【答案】(1)×;(2)×;(3)×;(4)√;(5)√。
4.如图,两条平行线间的3个三角形的面积关系是( )。
A. 不相等; B. 相等; C. 无法确定.
【答案】B
5. 一块三角形菜地,他的底是50m,高是30m,如果每平方米可种大白菜8棵,那么这块地一共可以种多少棵大白菜?如果平均每棵大白菜卖2元钱,那么这块地共收入多少元?
【答案】 12000
三、梯形的面积
【知识梳理】
1.梯形面积公式推导:
(1)方法一:运用拼摆法将两个完全一样的梯形拼成一个平行四边形。
将两个完全一样的梯形重叠在一起,一个梯形保持不动,另一个梯形绕任意一个顶点旋转180°,再平移,使两腰重合,即可拼成一个平行四边形。
平行四边形的底梯形的上底+下底;
平行四边形的高梯形的高;
梯形的面积=平行四边形的面积÷2=底×高÷2=(上底+下底)×高÷2。
(2)方法二:运用分割法把一个梯形分成两个三角形。
画出梯形的一条对角线,得到三角形①和三角形②,作出梯形的高。
梯形的面积=三角形①的面积+三角形②的面积=上底×高÷2+下底×高÷2。
【例题精讲】
例1.一个三角形与一个梯形的面积相等,高也相等,梯形的上底是3,下底是5,那么三角形的底是( ).
A. 5; B. 8; C. 10; D. 16.
【答案】B.
例2.填一填。
(1)梯形的上底是10厘米,下底和高相等,都是12厘米,它的面积是( )平方厘米。
(2)一个直角梯形上底是18厘米,如果下底,缩短4厘米,原来的梯形就变成了正方形,原来梯形的面积是( )平方厘米。
【答案】(1)132;(2)360。
例3.一个梯形的下底是上底的3倍,如果把上底延长8厘米,就得到一个平行四边形,且面积增加24平方厘米。这个梯形面积是多少平方厘米?
【解答】8÷2×(3+1)=16(厘米),24×2÷8=6(厘米),16×6÷2=48(平方厘米)。
【答案】48平方厘米
例4.填表。
【答案】9.8平方厘米,1.92平方厘米,1.2平方米,3平方厘米。
【巩固练习】
1.用48米长的篱笆,在靠墙的地方围一块菜地(如右下图)。这块菜地的面积是多少平
方米?如果按照每平方米菜地一年能收入16.5元计算,这块菜地一年能收人多少元?
【解答】(48-24)×24÷2=288(平方米),288×16.5=4752(元)。
【答案】4752元
2.一个梯形的上底是4cm,下底是6cm,高是3cm.沿直线只剪一刀,剪出一个最大的平行四边形,这个平行四边形的面积是( ).
A. 9; B. 12; C. 16.
【答案】B
3.求下面各梯形的面积。(单位:分米)
【解答】(5.6+3.4)×2.8÷2=12.6(平方分米);(14+12)×8÷2=104(平方分米)。
【答案】12.6平方分米;104平方分米。
4.比较图中两个阴影部分的面积,( )。
A. 甲=乙; B. 甲>乙; C. 甲<乙; D. 无法比较.
【答案】A
5.一个梯形的上底是,下底是10,高是8,它的面积是 ,当 时,它就是一个平行四边形.
【答案】,10.
【课堂检测】
1.如图所示,求梯形的面积。
【解答】17.8-6×2=5.8(cm)
【答案】5.8cm
2.汽车的前挡风玻璃是一个近似的梯形,上底为100,下底为132,高为55,如果这种玻璃的价格是每平方米660元,那么这块挡风玻璃的价钱是多少?
【答案】
3.比较平行线间的两个阴影部分面积(如下图),( )。
A. 甲>乙; B. 甲<乙; C. 甲=乙; D. 无法比较.
【答案】C
4.如图是一块长方形草坪,长16米,宽10米,中间有两条路,一条是平行四边形,一条是长方形。求草坪的面积。
【解答】16×10-2×16-2×10+2×2=112(平方米)
【答案】112平方米
5.一个三角形和一个平行四边形的面积相等,高也相等,如果三角形的底是18那么平行四边形的底是 .
【答案】9.
6. 求图中阴影部分的面积。
【答案】 2.8×3.2=9.24()
7. 三角形的底是,如果底边延长,面积就增加,原三角形的面积是多少平方米?
【答案】 7.5
8.如图,一个平行四边形和一个三角形拼成一个梯形,若梯形的面积是30cm2,则三角形的面积是 cm2.
【答案】10.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
12讲 基本图形面积
一、平行四边形的面积
【知识梳理】
1.等底等高的平行四边形面积相等。
2.(1)已知平行四边形的面积,和高,则平行四边形的底边;
(2)已知平行四边形的面积,和底边,则平行四边形的高。
3.平行四边形的面积=底×高。
如果用表示平行四边形的面积,用表示平行四边形的底,用表示平行四边形的高,那么平行四边形的面积计算公式可以写成:。
【说明】
(1)在同一个平行四边形中,不同的底与它对应的高的乘积相等,都等于这个平行四边形的面积;
(2)平行四边形的面积与它的底和高有关,底扩大到原来的倍(),高缩小到原来的,面积不变。
【注意】求平行四边形的面积,先要找到一组相对应的底和高,再计算。
4.平行四边形面积公式推导:
(1)方法一:沿着平行四边形地边上的高把平行四边形剪成一个直角三角形和一个直角梯形→把直角三角形向右平移后拼在直角梯形的右边→使平行四边形转化成长方形;
(2)方法二:用剪刀将平行四边形沿一条高剪开,剪成两个直角梯形,把左边的直角梯形向右平移后拼在另一个直角梯形的右边,使平行四边形转化成长方形。
长方形的长平行四边形的底;
长方形的宽平行四边形的高;
平行四边形的面积=长方形的面积=长×高=底×高。
【例题精讲】
例1.已知平行四边形的面积是300平方分米,如果它的底缩小到原来的一,高扩大到原来的5倍,那么面积为( )。
A. 50平方分米; B. 60平方分米; C. 360平方分米; D. 250平方分米.
例2.平行四边形的底扩大到原来的3倍,高不变,面积就( )
A. 不变; B. 扩大到原来的3倍; C. 扩大到原来的6倍. D. 略
例3.计算下面各图形的面积。
例4.把两个形状、大小完全相同的梯形拼成一个平行四边形,拼合后可以发现梯形的面积是平行四边形面积的 ,平行四边形的底=梯形的 ,平行四边形的高=梯形的 ,∵平行四边形的面积= (填写计算公式),∴梯形的面积= .(填写计算公式).
例5.有一块平行四边形的地,高是50米,底是高的1.2倍.给这块地铺植草皮,铺植1平方米草皮,需要18.5元,用草皮铺植这块地共需要多少元?
例6.下图平行四边形的面积是( )cm2。
A. 40; B. 48; C. 30.
【巩固练习】
1.如图,已知长方形的面积是 78,宽是6,长6,那么平行四边形的面积
.
2.如下图,正方形的周长是28,①的面积是15,求阴影部分的面积。
3.填一填。
(1)把一个平行四边形沿( )剪开,可以将它拼成一个( )形。转化后图形的( )和( )相当于平行四边形的( )和( ),转化前后图形的( )是不变的。因此,平行四边形的面积等于( )
(2)计算表中平行四边形的面积。
4. 一个平行四边形的周长是86(如图),以为底边时,对应的高是20,BC长为25,BC边上的高是多少厘米?
5.比较图中平行四边形的面积,( )。
A. ; B. ;
C. ; D. 无法比较.
二、三角形的面积
【知识梳理】
1.(1)已知三角形的面积,和高,则三角形的底边;
(2)已知三角形的面积,和底边,则三角形的高。
【例题精讲】
例1.一个三角形的底是1.2dm,高是0.5dm,这个三角形的面积是( )dm ,与它等底等高的平行四边形的面积是( )dm .
例2.用一张长方形纸剪同样的三角形(如下图),最多能剪成( )个这样的三角形。
A. 12
B. 24
C. 25
D. 10
例3.下图中的两个长方形面积相等,阴影部分的面积相比,甲( )乙。
A. 大于; B. 小于; C. 等于.
例4.有一个三角形的花圃,底是25米,高是22米。平均每平方米产鲜花20株,这个花圃一共可以产鲜花多少株?
【巩固练习】
1.如图,三角形的面积是( ),边上的高是 ( ) .
2.如图三角形(阴影部分)的面积是1平方米,平行四边形的面积是多少平方米?
3.判一判。
(1)两个面积相等的三角形可以拼成一个平行四边形。( )
(2)两个面积相等的三角形,底和高也相等。( )
(3)平行四边形的面积一定大于三角形的面积。( )
(4)等底等高的两个三角形面积相等。( )
(5)一个三角形和一个平行四边形面积相等,底也相等,三角形的高是4厘米,则平行四边形的高是2厘米。( )
4.如图,两条平行线间的3个三角形的面积关系是( )。
A. 不相等; B. 相等; C. 无法确定.
5. 一块三角形菜地,他的底是50m,高是30m,如果每平方米可种大白菜8棵,那么这块地一共可以种多少棵大白菜?如果平均每棵大白菜卖2元钱,那么这块地共收入多少元?
三、梯形的面积
【知识梳理】
1.梯形面积公式推导:
(1)方法一:运用拼摆法将两个完全一样的梯形拼成一个平行四边形。
将两个完全一样的梯形重叠在一起,一个梯形保持不动,另一个梯形绕任意一个顶点旋转180°,再平移,使两腰重合,即可拼成一个平行四边形。
平行四边形的底梯形的上底+下底;
平行四边形的高梯形的高;
梯形的面积=平行四边形的面积÷2=底×高÷2=(上底+下底)×高÷2。
(2)方法二:运用分割法把一个梯形分成两个三角形。
画出梯形的一条对角线,得到三角形①和三角形②,作出梯形的高。
梯形的面积=三角形①的面积+三角形②的面积=上底×高÷2+下底×高÷2。
【例题精讲】
例1.一个三角形与一个梯形的面积相等,高也相等,梯形的上底是3,下底是5,那么三角形的底是( ).
A. 5; B. 8; C. 10; D. 16.
例2.填一填。
(1)梯形的上底是10厘米,下底和高相等,都是12厘米,它的面积是( )平方厘米。
(2)一个直角梯形上底是18厘米,如果下底,缩短4厘米,原来的梯形就变成了正方形,原来梯形的面积是( )平方厘米。
例3.一个梯形的下底是上底的3倍,如果把上底延长8厘米,就得到一个平行四边形,且面积增加24平方厘米。这个梯形面积是多少平方厘米?
例4.填表。
【巩固练习】
1.用48米长的篱笆,在靠墙的地方围一块菜地(如右下图)。这块菜地的面积是多少平
方米?如果按照每平方米菜地一年能收入16.5元计算,这块菜地一年能收人多少元?
2.一个梯形的上底是4cm,下底是6cm,高是3cm.沿直线只剪一刀,剪出一个最大的平行四边形,这个平行四边形的面积是( ).
A. 9; B. 12; C. 16.
3.求下面各梯形的面积。(单位:分米)
4.比较图中两个阴影部分的面积,( )。
A. 甲=乙; B. 甲>乙; C. 甲<乙; D. 无法比较.
5.一个梯形的上底是,下底是10,高是8,它的面积是 ,当 时,它就是一个平行四边形.
【课堂检测】
1.如图所示,求梯形的面积。
2.汽车的前挡风玻璃是一个近似的梯形,上底为100,下底为132,高为55,如果这种玻璃的价格是每平方米660元,那么这块挡风玻璃的价钱是多少?
3.比较平行线间的两个阴影部分面积(如下图),( )。
A. 甲>乙; B. 甲<乙; C. 甲=乙; D. 无法比较.
4.如图是一块长方形草坪,长16米,宽10米,中间有两条路,一条是平行四边形,一条是长方形。求草坪的面积。
5.一个三角形和一个平行四边形的面积相等,高也相等,如果三角形的底是18cm,那么平行四边形的底是 .
6. 求图中阴影部分的面积。
7. 三角形的底是,如果底边延长,面积就增加,原三角形的面积是多少平方米?
8.如图,一个平行四边形和一个三角形拼成一个梯形,若梯形的面积是30cm2,则三角形的面积是 cm2.
参考答案
一、平行四边形的面积
【知识梳理】
1.等底等高的平行四边形面积相等。
2.(1)已知平行四边形的面积,和高,则平行四边形的底边;
(2)已知平行四边形的面积,和底边,则平行四边形的高。
3.平行四边形的面积=底×高。
如果用表示平行四边形的面积,用表示平行四边形的底,用表示平行四边形的高,那么平行四边形的面积计算公式可以写成:。
【说明】
(1)在同一个平行四边形中,不同的底与它对应的高的乘积相等,都等于这个平行四边形的面积;
(2)平行四边形的面积与它的底和高有关,底扩大到原来的倍(),高缩小到原来的,面积不变。
【注意】求平行四边形的面积,先要找到一组相对应的底和高,再计算。
4.平行四边形面积公式推导:
(1)方法一:沿着平行四边形地边上的高把平行四边形剪成一个直角三角形和一个直角梯形→把直角三角形向右平移后拼在直角梯形的右边→使平行四边形转化成长方形;
(2)方法二:用剪刀将平行四边形沿一条高剪开,剪成两个直角梯形,把左边的直角梯形向右平移后拼在另一个直角梯形的右边,使平行四边形转化成长方形。
长方形的长平行四边形的底;
长方形的宽平行四边形的高;
平行四边形的面积=长方形的面积=长×高=底×高。
【例题精讲】
例1.已知平行四边形的面积是300平方分米,如果它的底缩小到原来的一,高扩大到原来的5倍,那么面积为( )。
A. 50平方分米; B. 60平方分米; C. 360平方分米; D. 250平方分米.
【答案】D
例2.平行四边形的底扩大到原来的3倍,高不变,面积就( )
A. 不变; B. 扩大到原来的3倍; C. 扩大到原来的6倍. D. 略
【答案】B.
例3.计算下面各图形的面积。
【解答】4.5×2.4=10.8(cm2),3.8×1.5=5.7(cm2)。
【答案】10.8(cm2),5.7(cm2)
例4.把两个形状、大小完全相同的梯形拼成一个平行四边形,拼合后可以发现梯形的面积是平行四边形面积的 ,平行四边形的底=梯形的 ,平行四边形的高=梯形的 ,∵平行四边形的面积= (填写计算公式),∴梯形的面积= .(填写计算公式).
【答案】一半,上底与下底之和,高,底×高,(上底+下底)×高÷2.
例5.有一块平行四边形的地,高是50米,底是高的1.2倍.给这块地铺植草皮,铺植1平方米草皮,需要18.5元,用草皮铺植这块地共需要多少元?
【解答】解:底:50×1.2=60(米),
60×50×18.5=55500(元),
答:用草皮铺植这块地共需要55500元.
【答案】55500元.
例6.下图平行四边形的面积是( )cm2。
A. 40; B. 48; C. 30.
【答案】A
【巩固练习】
1.如图,已知长方形的面积是 78,宽是6,长6,那么平行四边形的面积
.
【答案】42.
2.如下图,正方形的周长是28,①的面积是15,求阴影部分的面积。
【答案】 28÷4=7() 7×7=49() 49-15=34()
3.填一填。
(1)把一个平行四边形沿( )剪开,可以将它拼成一个( )形。转化后图形的( )和( )相当于平行四边形的( )和( ),转化前后图形的( )是不变的。因此,平行四边形的面积等于( )
(2)计算表中平行四边形的面积。
【答案】(1)高,长方,长,宽,底,高,面积,底×高;(2)336,20.65,0.3。
4. 一个平行四边形的周长是86(如图),以为底边时,对应的高是20,BC长为25,BC边上的高是多少厘米?
【答案】 86÷2-25=18() 18×20÷25=14.4()
5.比较图中平行四边形的面积,( )。
A. ; B. ;
C. ; D. 无法比较.
【答案】C
二、三角形的面积
【知识梳理】
1.(1)已知三角形的面积,和高,则三角形的底边;
(2)已知三角形的面积,和底边,则三角形的高。
【例题精讲】
例1.一个三角形的底是1.2dm,高是0.5dm,这个三角形的面积是( )dm ,与它等底等高的平行四边形的面积是( )dm .
【答案】0.3,0.6
例2.用一张长方形纸剪同样的三角形(如下图),最多能剪成( )个这样的三角形。
A. 12
B. 24
C. 25
D. 10
【答案】B
例3.下图中的两个长方形面积相等,阴影部分的面积相比,甲( )乙。
A. 大于; B. 小于; C. 等于.
【答案】C
例4.有一个三角形的花圃,底是25米,高是22米。平均每平方米产鲜花20株,这个花圃一共可以产鲜花多少株?
【解答】25×22÷2×20=5500(株)
【答案】5500株
【巩固练习】
1.如图,三角形的面积是( ),边上的高是 ( ) .
【答案】24,4.8.
2.如图三角形(阴影部分)的面积是1平方米,平行四边形的面积是多少平方米?
【解答】1×2÷2=1(米),(2+1)×2=6(平方米)。
【答案】6平方米
3.判一判。
(1)两个面积相等的三角形可以拼成一个平行四边形。( )
(2)两个面积相等的三角形,底和高也相等。( )
(3)平行四边形的面积一定大于三角形的面积。( )
(4)等底等高的两个三角形面积相等。( )
(5)一个三角形和一个平行四边形面积相等,底也相等,三角形的高是4厘米,则平行四边形的高是2厘米。( )
【答案】(1)×;(2)×;(3)×;(4)√;(5)√。
4.如图,两条平行线间的3个三角形的面积关系是( )。
A. 不相等; B. 相等; C. 无法确定.
【答案】B
5. 一块三角形菜地,他的底是50m,高是30m,如果每平方米可种大白菜8棵,那么这块地一共可以种多少棵大白菜?如果平均每棵大白菜卖2元钱,那么这块地共收入多少元?
【答案】 12000
三、梯形的面积
【知识梳理】
1.梯形面积公式推导:
(1)方法一:运用拼摆法将两个完全一样的梯形拼成一个平行四边形。
将两个完全一样的梯形重叠在一起,一个梯形保持不动,另一个梯形绕任意一个顶点旋转180°,再平移,使两腰重合,即可拼成一个平行四边形。
平行四边形的底梯形的上底+下底;
平行四边形的高梯形的高;
梯形的面积=平行四边形的面积÷2=底×高÷2=(上底+下底)×高÷2。
(2)方法二:运用分割法把一个梯形分成两个三角形。
画出梯形的一条对角线,得到三角形①和三角形②,作出梯形的高。
梯形的面积=三角形①的面积+三角形②的面积=上底×高÷2+下底×高÷2。
【例题精讲】
例1.一个三角形与一个梯形的面积相等,高也相等,梯形的上底是3,下底是5,那么三角形的底是( ).
A. 5; B. 8; C. 10; D. 16.
【答案】B.
例2.填一填。
(1)梯形的上底是10厘米,下底和高相等,都是12厘米,它的面积是( )平方厘米。
(2)一个直角梯形上底是18厘米,如果下底,缩短4厘米,原来的梯形就变成了正方形,原来梯形的面积是( )平方厘米。
【答案】(1)132;(2)360。
例3.一个梯形的下底是上底的3倍,如果把上底延长8厘米,就得到一个平行四边形,且面积增加24平方厘米。这个梯形面积是多少平方厘米?
【解答】8÷2×(3+1)=16(厘米),24×2÷8=6(厘米),16×6÷2=48(平方厘米)。
【答案】48平方厘米
例4.填表。
【答案】9.8平方厘米,1.92平方厘米,1.2平方米,3平方厘米。
【巩固练习】
1.用48米长的篱笆,在靠墙的地方围一块菜地(如右下图)。这块菜地的面积是多少平
方米?如果按照每平方米菜地一年能收入16.5元计算,这块菜地一年能收人多少元?
【解答】(48-24)×24÷2=288(平方米),288×16.5=4752(元)。
【答案】4752元
2.一个梯形的上底是4cm,下底是6cm,高是3cm.沿直线只剪一刀,剪出一个最大的平行四边形,这个平行四边形的面积是( ).
A. 9; B. 12; C. 16.
【答案】B
3.求下面各梯形的面积。(单位:分米)
【解答】(5.6+3.4)×2.8÷2=12.6(平方分米);(14+12)×8÷2=104(平方分米)。
【答案】12.6平方分米;104平方分米。
4.比较图中两个阴影部分的面积,( )。
A. 甲=乙; B. 甲>乙; C. 甲<乙; D. 无法比较.
【答案】A
5.一个梯形的上底是,下底是10,高是8,它的面积是 ,当 时,它就是一个平行四边形.
【答案】,10.
【课堂检测】
1.如图所示,求梯形的面积。
【解答】17.8-6×2=5.8(cm)
【答案】5.8cm
2.汽车的前挡风玻璃是一个近似的梯形,上底为100,下底为132,高为55,如果这种玻璃的价格是每平方米660元,那么这块挡风玻璃的价钱是多少?
【答案】
3.比较平行线间的两个阴影部分面积(如下图),( )。
A. 甲>乙; B. 甲<乙; C. 甲=乙; D. 无法比较.
【答案】C
4.如图是一块长方形草坪,长16米,宽10米,中间有两条路,一条是平行四边形,一条是长方形。求草坪的面积。
【解答】16×10-2×16-2×10+2×2=112(平方米)
【答案】112平方米
5.一个三角形和一个平行四边形的面积相等,高也相等,如果三角形的底是18那么平行四边形的底是 .
【答案】9.
6. 求图中阴影部分的面积。
【答案】 2.8×3.2=9.24()
7. 三角形的底是,如果底边延长,面积就增加,原三角形的面积是多少平方米?
【答案】 7.5
8.如图,一个平行四边形和一个三角形拼成一个梯形,若梯形的面积是30cm2,则三角形的面积是 cm2.
【答案】10.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
