人教版 五年级数学上册13讲组合图形面积学案
文档属性
| 名称 | 人教版 五年级数学上册13讲组合图形面积学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-29 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
13讲 组合图形面积
一、组合图形的面积
【知识梳理】
1.估算不规则图形的面积时,可以先通过数方格确定面积的范围,再将不满一格的都按半格计算,也可根据图形的特点转化成已学过的图形,再利用面积公式来估算面积。
2.通过画辅助线的方法可以将不规则图形转化成几个基本图形,从而使问题得到简化。
(1)当组合图形是凸出的,用虚线分割成几种简单图形,把简单图形面积相加计算.
(2)当组合图形是凹陷的,用虚线补齐成一种最大的简单图形,用最大简单图形面积减几个较小的简单图形面积进行计算.
【说明】将组合图形分成几个简单图形,计算每个简单图形的面积时要找准数据。
【注意】将组合图形进行分割时,一定要考虑到分别求面积时所需要的数据条件是否充分。
3.计算组合图形的面积,要根据已知条件对图形进行分割,转化成已学过的简单图形,先分别计算出它们的面积,再求和或差。
【例题精讲】
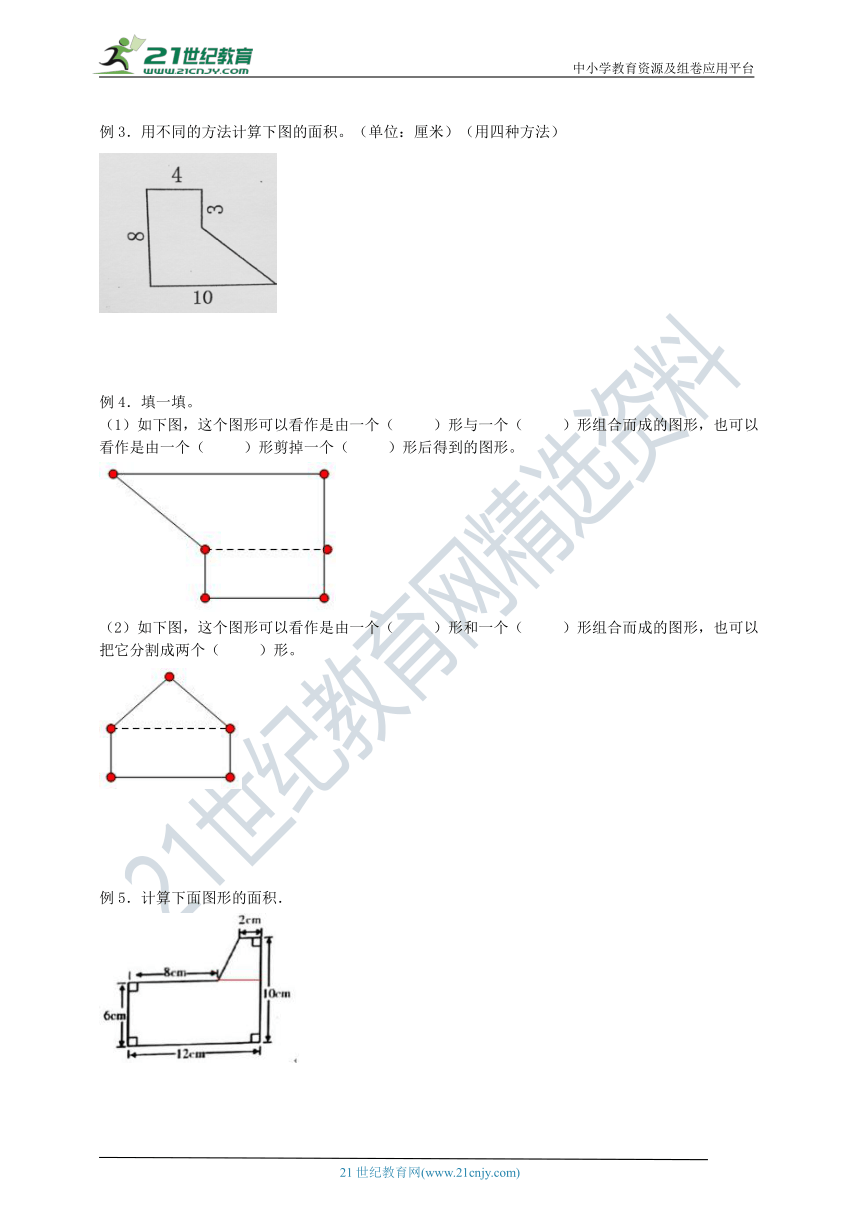
例1.如果粉刷这面墙每平方米需要花费2.5元,那么粉刷这面墙共需花费多少元?
例2.用分割法计算下面图形的面积。(单位:厘米)
例3.用不同的方法计算下图的面积。(单位:厘米)(用四种方法)
例4.填一填。
(1)如下图,这个图形可以看作是由一个( )形与一个( )形组合而成的图形,也可以看作是由一个( )形剪掉一个( )形后得到的图形。
(2)如下图,这个图形可以看作是由一个( )形和一个( )形组合而成的图形,也可以把它分割成两个( )形。
例5.计算下面图形的面积.
【巩固练习】
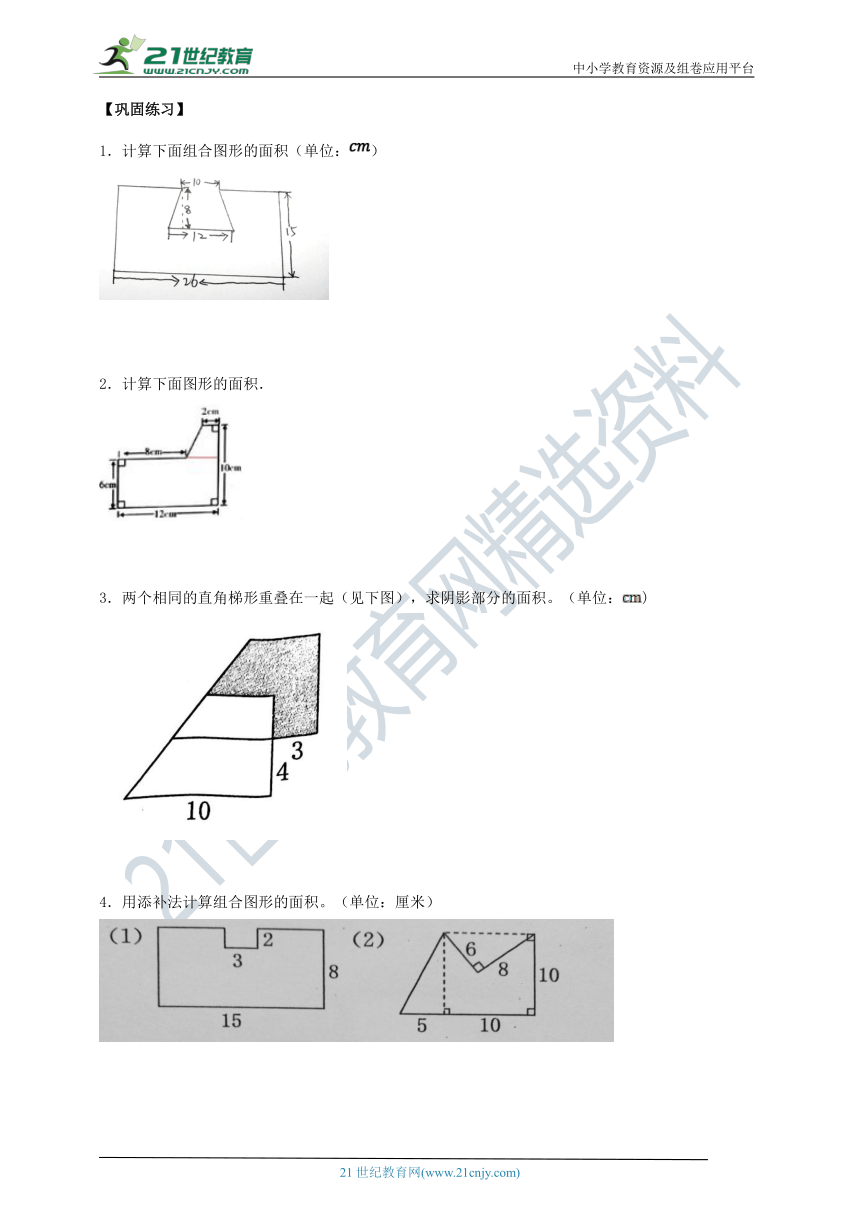
1.计算下面组合图形的面积(单位:)
2.计算下面图形的面积.
3.两个相同的直角梯形重叠在一起(见下图),求阴影部分的面积。(单位:)
4.用添补法计算组合图形的面积。(单位:厘米)
二、多边形的面积 综合复习
【知识梳理】
1.
【例题精讲】
例1.如图,已知平行四边形的面积为18平方厘米,BE=2EC,CF=FD,则阴影三角形的面积是多少平方厘米?
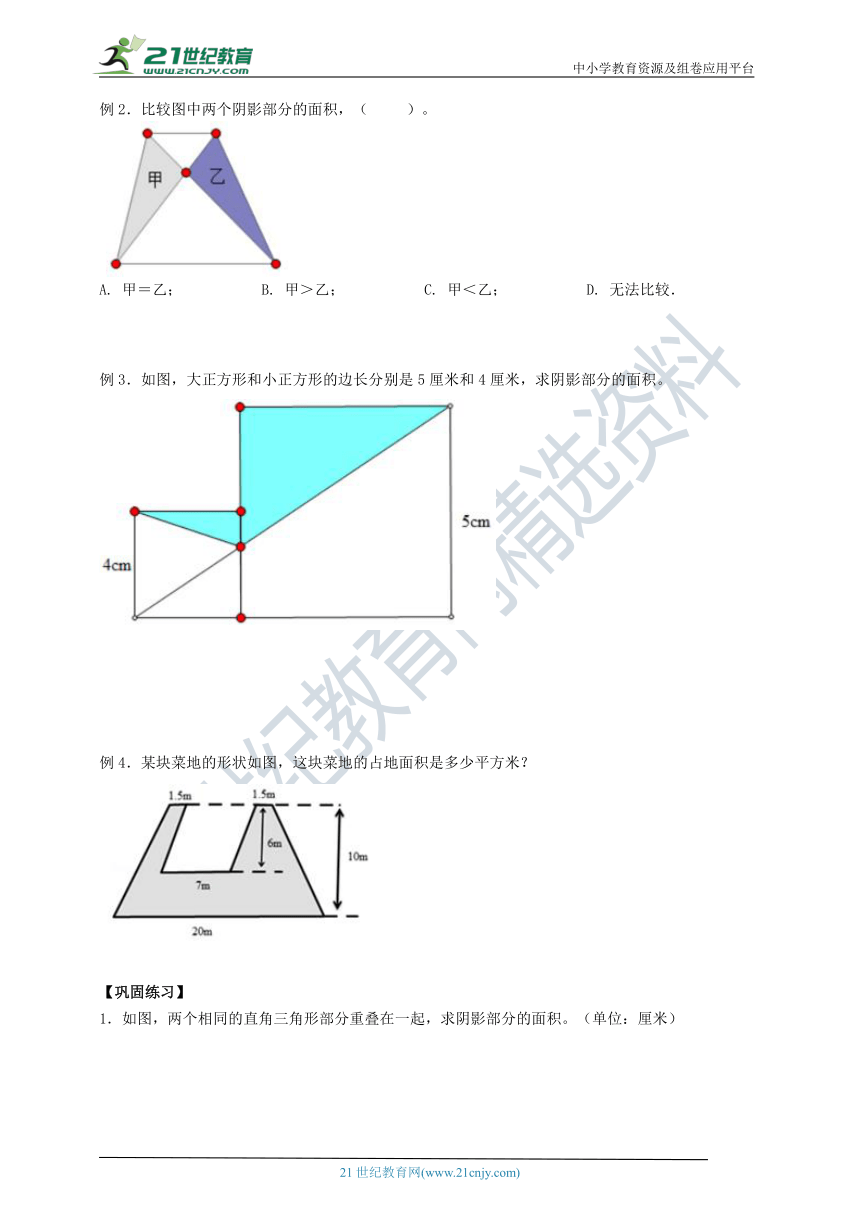
例2.比较图中两个阴影部分的面积,( )。
A. 甲=乙; B. 甲>乙; C. 甲<乙; D. 无法比较.
例3.如图,大正方形和小正方形的边长分别是5厘米和4厘米,求阴影部分的面积。
例4.某块菜地的形状如图,这块菜地的占地面积是多少平方米?
【巩固练习】
1.如图,两个相同的直角三角形部分重叠在一起,求阴影部分的面积。(单位:厘米)
2.如图,大梯形的上底是12cm,高是15cm,阴影部分的面积是36cm2,求大梯形的面积。
3.下图中,两个正方形的边长分别是4厘米和2厘米,求图中阴影部分的面积。
4.下图是一个大正方形和一个小正方形拼成的图形。已知小正方形的边长为5厘米,阴影部分的面积是45平方厘米。你能求出空白部分的面积吗?
【课堂检测】
1.求图中阴影部分的面积。(单位:厘米)
2.下面组合图形可以分成哪些已学过的图形?请你在图中画一画。
3.比较平行线间的两个阴影部分面积(如下图),( )。
A. 甲>乙; B. 甲<乙; C. 甲=乙; D. 无法比较.
4.一块梯形草地中间有一条长8米,宽1米的长方形小路(如图,单位m),这块草地的面积是多少平方米?
5.计算组合图形的面积
【答案】1860
6.图中每个小方格的面积为1cm ,五角星图(阴影部分)的面积约( )1cm .
A. 26~30 B. 19~25 C. 9~18 D. 4~8
7.求下面图形的面积。
8.一块梯形地,上底是40,下底是60,高是40(如图)。李伯伯在这块地最大的一块正方形地里种棉花,其余的种花生,种花生的面积有多大?
参考答案
一、组合图形的面积
【知识梳理】
1.估算不规则图形的面积时,可以先通过数方格确定面积的范围,再将不满一格的都按半格计算,也可根据图形的特点转化成已学过的图形,再利用面积公式来估算面积。
2.通过画辅助线的方法可以将不规则图形转化成几个基本图形,从而使问题得到简化。
(1)当组合图形是凸出的,用虚线分割成几种简单图形,把简单图形面积相加计算.
(2)当组合图形是凹陷的,用虚线补齐成一种最大的简单图形,用最大简单图形面积减几个较小的简单图形面积进行计算.
【说明】将组合图形分成几个简单图形,计算每个简单图形的面积时要找准数据。
【注意】将组合图形进行分割时,一定要考虑到分别求面积时所需要的数据条件是否充分。
3.计算组合图形的面积,要根据已知条件对图形进行分割,转化成已学过的简单图形,先分别计算出它们的面积,再求和或差。
【例题精讲】
例1.如果粉刷这面墙每平方米需要花费2.5元,那么粉刷这面墙共需花费多少元?
【解答】3×8+8×1.4÷2=29.6(平方米),29.6×2.5=74(元)。
【答案】74元
例2.用分割法计算下面图形的面积。(单位:厘米)
【答案】(1)1.54242227(平方厘米)
(2)(1016)12216102=236(平方厘米)
(3)101015202=250(平方厘米)
(4)2010208=360(平方厘米)
例3.用不同的方法计算下图的面积。(单位:厘米)(用四种方法)
【答案】方法一:34(410)(83)2123547(平方厘米)
方法二:84(83)(104)2321547(平方厘米)
方法三:810(83)(104)2803347(平方厘米)
方法四:(83)42(83)102222547(平方厘米)
例4.填一填。
(1)如下图,这个图形可以看作是由一个( )形与一个( )形组合而成的图形,也可以看作是由一个( )形剪掉一个( )形后得到的图形。
(2)如下图,这个图形可以看作是由一个( )形和一个( )形组合而成的图形,也可以把它分割成两个( )形。
【答案】(1)梯,长方,长方,梯(后两空或梯,三角);(2)三角,长方,梯。
例5.计算下面图形的面积.
【解答】解:将原图形切割成两个部分,总面积=梯形面积+长方形面积.
长方形面积=12×6=72(平方厘米),
梯形面积=(2+12-8)×(10-6)÷2=12(平方厘米),
总面积:72+12=84(平方厘米).
【答案】84.
【巩固练习】
1.计算下面组合图形的面积(单位:)
【解答】解:长方形面积26×15=390(),
梯形面积:(10+12)×8÷2=88(),
390—88=308().
【答案】308.
2.计算下面图形的面积.
【解答】解:将原图形切割成两个部分,总面积=梯形面积+长方形面积.
长方形面积=12×6=72(平方厘米),
梯形面积=(2+12-8)×(10-6)÷2=12(平方厘米),
总面积:72+12=84(平方厘米).
【答案】84.
3.两个相同的直角梯形重叠在一起(见下图),求阴影部分的面积。(单位:)
【答案】103=7() (710)42=34()
4.用添补法计算组合图形的面积。(单位:厘米)
【答案】(1)15832114(平方厘米)
(2)(10105)102682=101(平方厘米)
(3)13201252=230(平方厘米)
(4)(1020)222862=306(平方厘米)
二、多边形的面积 综合复习
【知识梳理】
1.
【例题精讲】
例1.如图,已知平行四边形的面积为18平方厘米,BE=2EC,CF=FD,则阴影三角形的面积是多少平方厘米?
【解答】三角形ABE的面积是18÷(2+1)×2÷2=6(平方厘米),三角形ADF的面积是18÷2÷2=4.5(平方厘米),三角形CEF的面积是18÷(2+1)÷2÷2=1.5(平方厘米),所以阴影部分的面积为18-6-4.5-1.5=6(平方厘米)。
【答案】6平方厘米
例2.比较图中两个阴影部分的面积,( )。
A. 甲=乙; B. 甲>乙; C. 甲<乙; D. 无法比较.
【答案】A
例3.如图,大正方形和小正方形的边长分别是5厘米和4厘米,求阴影部分的面积。
【解答】4×4+5×5=41(平方厘米),4×4÷2=8(平方厘米),5×(5+4)÷2=22.5(平方厘米),41-8-22.5=10.5(平方厘米)
【答案】10.5平方厘米
例4.某块菜地的形状如图,这块菜地的占地面积是多少平方米?
【解答】解:梯形的面积:(1.5×2+7+20)×10÷2=30×10÷2=150(平方米)
平行四边形的面积:7×6=42(平方米)
菜地面积:150﹣42=108(平方米)
答:这块菜地的占地面积是108平方米.
【答案】108平方米.
【巩固练习】
1.如图,两个相同的直角三角形部分重叠在一起,求阴影部分的面积。(单位:厘米)
【解答】[(8-3)+8]×5÷2=32.5(平方厘米)
【答案】32.5平方厘米
2.如图,大梯形的上底是12cm,高是15cm,阴影部分的面积是36cm2,求大梯形的面积。
【解答】36cm2是以12cm为底、15cm为高的大三角形面积减去阴影左边小三角形面积。
小三角形面积:12×15÷2-36=54(cm2)
小三角形的高a:54×2÷12=9(cm)
阴影部分的高b:36×2÷9=8(cm)
梯形下底:12+8=20(cm)
梯形面积:(12+20)×15÷2=240(cm2)
【答案】240cm2
3.下图中,两个正方形的边长分别是4厘米和2厘米,求图中阴影部分的面积。
【解答】4×4÷2+2×2-(4+2)×2÷2=6(平方厘米)
【答案】6平方厘米
4.下图是一个大正方形和一个小正方形拼成的图形。已知小正方形的边长为5厘米,阴影部分的面积是45平方厘米。你能求出空白部分的面积吗?
【解答】45-5×5=20(平方厘米),20×2÷5=8(厘米),8×8-20=44(平方厘米)
提示:阴影部分面积减去小正方形面积得三角形而积,再根据这个三角形面积求出大正方形的边长。
【答案】44平方厘米
【课堂检测】
1.求图中阴影部分的面积。(单位:厘米)
【解答】5×5+4×4-(6+2)×(5+4)÷2=9.5(平方厘米)
【答案】9.5平方厘米
2.下面组合图形可以分成哪些已学过的图形?请你在图中画一画。
【答案】
3.比较平行线间的两个阴影部分面积(如下图),( )。
A. 甲>乙; B. 甲<乙; C. 甲=乙; D. 无法比较.
【答案】C
4.一块梯形草地中间有一条长8米,宽1米的长方形小路(如图,单位m),这块草地的面积是多少平方米?
【答案】152 平方米
5.计算组合图形的面积
【答案】1860
6.图中每个小方格的面积为1cm ,五角星图(阴影部分)的面积约( )1cm .
A. 26~30 B. 19~25 C. 9~18 D. 4~8
【答案】C
7.求下面图形的面积。
【解答】19×6+19×4÷2=152(m2);
12×4+(12+15)(10-4)÷2=129(cm2) 。
【答案】152m2;129cm2
8.一块梯形地,上底是40,下底是60,高是40(如图)。李伯伯在这块地最大的一块正方形地里种棉花,其余的种花生,种花生的面积有多大?
【答案】(6040)402=2000()
4040=1600() 20001600=400()
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
13讲 组合图形面积
一、组合图形的面积
【知识梳理】
1.估算不规则图形的面积时,可以先通过数方格确定面积的范围,再将不满一格的都按半格计算,也可根据图形的特点转化成已学过的图形,再利用面积公式来估算面积。
2.通过画辅助线的方法可以将不规则图形转化成几个基本图形,从而使问题得到简化。
(1)当组合图形是凸出的,用虚线分割成几种简单图形,把简单图形面积相加计算.
(2)当组合图形是凹陷的,用虚线补齐成一种最大的简单图形,用最大简单图形面积减几个较小的简单图形面积进行计算.
【说明】将组合图形分成几个简单图形,计算每个简单图形的面积时要找准数据。
【注意】将组合图形进行分割时,一定要考虑到分别求面积时所需要的数据条件是否充分。
3.计算组合图形的面积,要根据已知条件对图形进行分割,转化成已学过的简单图形,先分别计算出它们的面积,再求和或差。
【例题精讲】
例1.如果粉刷这面墙每平方米需要花费2.5元,那么粉刷这面墙共需花费多少元?
例2.用分割法计算下面图形的面积。(单位:厘米)
例3.用不同的方法计算下图的面积。(单位:厘米)(用四种方法)
例4.填一填。
(1)如下图,这个图形可以看作是由一个( )形与一个( )形组合而成的图形,也可以看作是由一个( )形剪掉一个( )形后得到的图形。
(2)如下图,这个图形可以看作是由一个( )形和一个( )形组合而成的图形,也可以把它分割成两个( )形。
例5.计算下面图形的面积.
【巩固练习】
1.计算下面组合图形的面积(单位:)
2.计算下面图形的面积.
3.两个相同的直角梯形重叠在一起(见下图),求阴影部分的面积。(单位:)
4.用添补法计算组合图形的面积。(单位:厘米)
二、多边形的面积 综合复习
【知识梳理】
1.
【例题精讲】
例1.如图,已知平行四边形的面积为18平方厘米,BE=2EC,CF=FD,则阴影三角形的面积是多少平方厘米?
例2.比较图中两个阴影部分的面积,( )。
A. 甲=乙; B. 甲>乙; C. 甲<乙; D. 无法比较.
例3.如图,大正方形和小正方形的边长分别是5厘米和4厘米,求阴影部分的面积。
例4.某块菜地的形状如图,这块菜地的占地面积是多少平方米?
【巩固练习】
1.如图,两个相同的直角三角形部分重叠在一起,求阴影部分的面积。(单位:厘米)
2.如图,大梯形的上底是12cm,高是15cm,阴影部分的面积是36cm2,求大梯形的面积。
3.下图中,两个正方形的边长分别是4厘米和2厘米,求图中阴影部分的面积。
4.下图是一个大正方形和一个小正方形拼成的图形。已知小正方形的边长为5厘米,阴影部分的面积是45平方厘米。你能求出空白部分的面积吗?
【课堂检测】
1.求图中阴影部分的面积。(单位:厘米)
2.下面组合图形可以分成哪些已学过的图形?请你在图中画一画。
3.比较平行线间的两个阴影部分面积(如下图),( )。
A. 甲>乙; B. 甲<乙; C. 甲=乙; D. 无法比较.
4.一块梯形草地中间有一条长8米,宽1米的长方形小路(如图,单位m),这块草地的面积是多少平方米?
5.计算组合图形的面积
【答案】1860
6.图中每个小方格的面积为1cm ,五角星图(阴影部分)的面积约( )1cm .
A. 26~30 B. 19~25 C. 9~18 D. 4~8
7.求下面图形的面积。
8.一块梯形地,上底是40,下底是60,高是40(如图)。李伯伯在这块地最大的一块正方形地里种棉花,其余的种花生,种花生的面积有多大?
参考答案
一、组合图形的面积
【知识梳理】
1.估算不规则图形的面积时,可以先通过数方格确定面积的范围,再将不满一格的都按半格计算,也可根据图形的特点转化成已学过的图形,再利用面积公式来估算面积。
2.通过画辅助线的方法可以将不规则图形转化成几个基本图形,从而使问题得到简化。
(1)当组合图形是凸出的,用虚线分割成几种简单图形,把简单图形面积相加计算.
(2)当组合图形是凹陷的,用虚线补齐成一种最大的简单图形,用最大简单图形面积减几个较小的简单图形面积进行计算.
【说明】将组合图形分成几个简单图形,计算每个简单图形的面积时要找准数据。
【注意】将组合图形进行分割时,一定要考虑到分别求面积时所需要的数据条件是否充分。
3.计算组合图形的面积,要根据已知条件对图形进行分割,转化成已学过的简单图形,先分别计算出它们的面积,再求和或差。
【例题精讲】
例1.如果粉刷这面墙每平方米需要花费2.5元,那么粉刷这面墙共需花费多少元?
【解答】3×8+8×1.4÷2=29.6(平方米),29.6×2.5=74(元)。
【答案】74元
例2.用分割法计算下面图形的面积。(单位:厘米)
【答案】(1)1.54242227(平方厘米)
(2)(1016)12216102=236(平方厘米)
(3)101015202=250(平方厘米)
(4)2010208=360(平方厘米)
例3.用不同的方法计算下图的面积。(单位:厘米)(用四种方法)
【答案】方法一:34(410)(83)2123547(平方厘米)
方法二:84(83)(104)2321547(平方厘米)
方法三:810(83)(104)2803347(平方厘米)
方法四:(83)42(83)102222547(平方厘米)
例4.填一填。
(1)如下图,这个图形可以看作是由一个( )形与一个( )形组合而成的图形,也可以看作是由一个( )形剪掉一个( )形后得到的图形。
(2)如下图,这个图形可以看作是由一个( )形和一个( )形组合而成的图形,也可以把它分割成两个( )形。
【答案】(1)梯,长方,长方,梯(后两空或梯,三角);(2)三角,长方,梯。
例5.计算下面图形的面积.
【解答】解:将原图形切割成两个部分,总面积=梯形面积+长方形面积.
长方形面积=12×6=72(平方厘米),
梯形面积=(2+12-8)×(10-6)÷2=12(平方厘米),
总面积:72+12=84(平方厘米).
【答案】84.
【巩固练习】
1.计算下面组合图形的面积(单位:)
【解答】解:长方形面积26×15=390(),
梯形面积:(10+12)×8÷2=88(),
390—88=308().
【答案】308.
2.计算下面图形的面积.
【解答】解:将原图形切割成两个部分,总面积=梯形面积+长方形面积.
长方形面积=12×6=72(平方厘米),
梯形面积=(2+12-8)×(10-6)÷2=12(平方厘米),
总面积:72+12=84(平方厘米).
【答案】84.
3.两个相同的直角梯形重叠在一起(见下图),求阴影部分的面积。(单位:)
【答案】103=7() (710)42=34()
4.用添补法计算组合图形的面积。(单位:厘米)
【答案】(1)15832114(平方厘米)
(2)(10105)102682=101(平方厘米)
(3)13201252=230(平方厘米)
(4)(1020)222862=306(平方厘米)
二、多边形的面积 综合复习
【知识梳理】
1.
【例题精讲】
例1.如图,已知平行四边形的面积为18平方厘米,BE=2EC,CF=FD,则阴影三角形的面积是多少平方厘米?
【解答】三角形ABE的面积是18÷(2+1)×2÷2=6(平方厘米),三角形ADF的面积是18÷2÷2=4.5(平方厘米),三角形CEF的面积是18÷(2+1)÷2÷2=1.5(平方厘米),所以阴影部分的面积为18-6-4.5-1.5=6(平方厘米)。
【答案】6平方厘米
例2.比较图中两个阴影部分的面积,( )。
A. 甲=乙; B. 甲>乙; C. 甲<乙; D. 无法比较.
【答案】A
例3.如图,大正方形和小正方形的边长分别是5厘米和4厘米,求阴影部分的面积。
【解答】4×4+5×5=41(平方厘米),4×4÷2=8(平方厘米),5×(5+4)÷2=22.5(平方厘米),41-8-22.5=10.5(平方厘米)
【答案】10.5平方厘米
例4.某块菜地的形状如图,这块菜地的占地面积是多少平方米?
【解答】解:梯形的面积:(1.5×2+7+20)×10÷2=30×10÷2=150(平方米)
平行四边形的面积:7×6=42(平方米)
菜地面积:150﹣42=108(平方米)
答:这块菜地的占地面积是108平方米.
【答案】108平方米.
【巩固练习】
1.如图,两个相同的直角三角形部分重叠在一起,求阴影部分的面积。(单位:厘米)
【解答】[(8-3)+8]×5÷2=32.5(平方厘米)
【答案】32.5平方厘米
2.如图,大梯形的上底是12cm,高是15cm,阴影部分的面积是36cm2,求大梯形的面积。
【解答】36cm2是以12cm为底、15cm为高的大三角形面积减去阴影左边小三角形面积。
小三角形面积:12×15÷2-36=54(cm2)
小三角形的高a:54×2÷12=9(cm)
阴影部分的高b:36×2÷9=8(cm)
梯形下底:12+8=20(cm)
梯形面积:(12+20)×15÷2=240(cm2)
【答案】240cm2
3.下图中,两个正方形的边长分别是4厘米和2厘米,求图中阴影部分的面积。
【解答】4×4÷2+2×2-(4+2)×2÷2=6(平方厘米)
【答案】6平方厘米
4.下图是一个大正方形和一个小正方形拼成的图形。已知小正方形的边长为5厘米,阴影部分的面积是45平方厘米。你能求出空白部分的面积吗?
【解答】45-5×5=20(平方厘米),20×2÷5=8(厘米),8×8-20=44(平方厘米)
提示:阴影部分面积减去小正方形面积得三角形而积,再根据这个三角形面积求出大正方形的边长。
【答案】44平方厘米
【课堂检测】
1.求图中阴影部分的面积。(单位:厘米)
【解答】5×5+4×4-(6+2)×(5+4)÷2=9.5(平方厘米)
【答案】9.5平方厘米
2.下面组合图形可以分成哪些已学过的图形?请你在图中画一画。
【答案】
3.比较平行线间的两个阴影部分面积(如下图),( )。
A. 甲>乙; B. 甲<乙; C. 甲=乙; D. 无法比较.
【答案】C
4.一块梯形草地中间有一条长8米,宽1米的长方形小路(如图,单位m),这块草地的面积是多少平方米?
【答案】152 平方米
5.计算组合图形的面积
【答案】1860
6.图中每个小方格的面积为1cm ,五角星图(阴影部分)的面积约( )1cm .
A. 26~30 B. 19~25 C. 9~18 D. 4~8
【答案】C
7.求下面图形的面积。
【解答】19×6+19×4÷2=152(m2);
12×4+(12+15)(10-4)÷2=129(cm2) 。
【答案】152m2;129cm2
8.一块梯形地,上底是40,下底是60,高是40(如图)。李伯伯在这块地最大的一块正方形地里种棉花,其余的种花生,种花生的面积有多大?
【答案】(6040)402=2000()
4040=1600() 20001600=400()
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
