1.4.1 充分条件与必要条件 课件(共21张PPT)
文档属性
| 名称 | 1.4.1 充分条件与必要条件 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 236.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-02 11:52:13 | ||
图片预览







文档简介
第一章 集合与常用逻辑用语
1.4.1 充分条件与必要条件
教学目标
1.知识与技能
理解充分条件、必要条件的定义;会判断条件与结论的关系,会判断命题的充分条件、必要条件.
2.过程与方法
通过判断p与q的关系引导充要条件的定义,由诱导探究的方法归纳出判断“p是q的什么条件”步骤及方法.
3.情感、态度与价值观
让学生通过练题总结归纳,培养学生理解、分析、归纳、解决问题的能力;从实际例子体会数学的有用性,“在生活中数学地思维”,增强对数学逻辑知识的兴趣,激发学生的数学兴趣。
重点难点
[重点]
1.充分条件、必要条件、充要条件的概念;
2.充分条件、必要条件与判定定理、性质定理的关系.
[难点]
命题的充分条件、必要条件的判断;
充要条件的理解与判断。
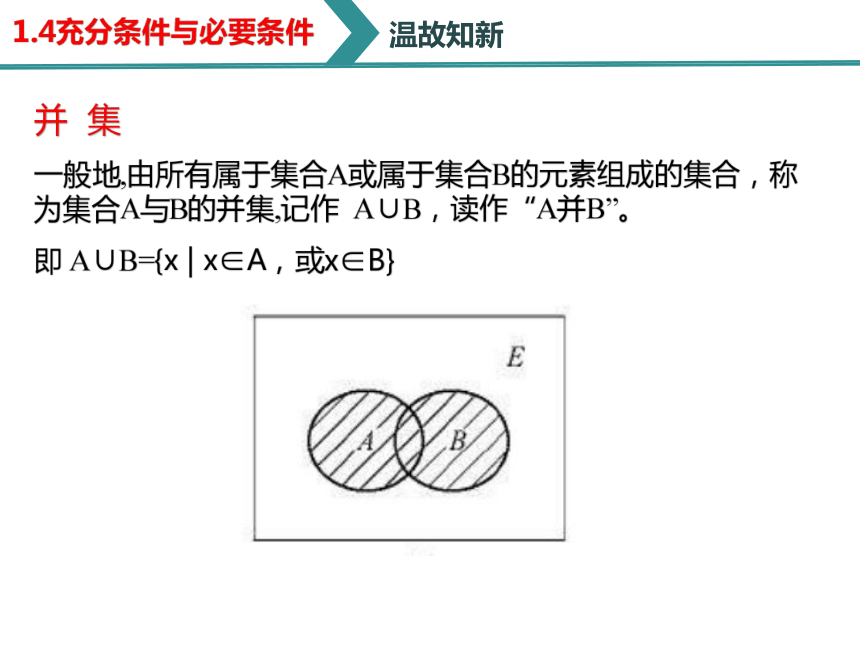
并 集
一般地,由所有属于集合A或属于集合B的元素组成的集合,称为集合A与B的并集,记作 A∪B,读作“A并B”。
即 A∪B={x | x∈A,或x∈B}
温故知新
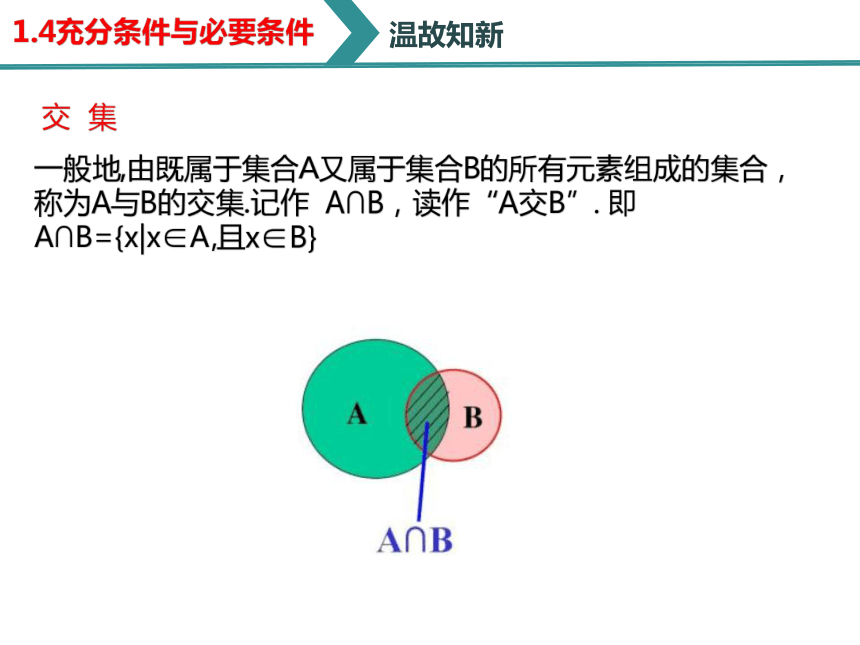
交 集
一般地,由既属于集合A又属于集合B的所有元素组成的集合,称为A与B的交集.记作 A∩B,读作“A交B”. 即 A∩B={x|x∈A,且x∈B}
温故知新
补 集
对于一个集合A,由全集U中不属于A的所有元素组成的集合称为集合A相对于全集U的补集,简称为集合A的补集,记作CuA.即CuA ={x|x∈U,且x?A}
温故知新
新课导入
在初中,我们对命题已经有了初步的认识。
一般地,我们把用语言、符号或式子表达的, 可以判断真假的陈述句叫做命题。 其中,
判断为真的命题叫真命题;
判断为假的命题叫假命题。
很多命题可以写成“若 p ,则 q ”或“如果 p ,那么 q ”
“若 p ,则 q ”形式的命题中的 p 称为命题的条件, q 称为命题的结论。
问题思考
思考?
指出下列两个命题的条件和结论,并判断是真命题还是假命题?
(1)若a2=b2,则a=b;
(2)若ab=0,则a=0或b=0;
命题(1)为假命题,条件:a2=b2,结论a=b。
命题(2)为真命题.条件:ab=0,结论a=0或b=0。
充分条件与必要条件定义
知识点一
充分条件与必要条件定义
一般地,“若p,则q”为真命题,是指由p通过推理可以得出q.这时,我们就说,由p可推出q,记作:
p?q.
定义:如果命题“若p,则q”为真命题,即p?q,那么我们就说p是q的充分条件;q是p必要条件.
典型例题——充分条件
解:(1)(3)为真命题,(2)是假命题,
所以(1)(3)的p是q的充分条件;
典型例题——必要条件
解:(2)(3)为真命题,(1)是假命题,
所以(2)(3)的p是q的充分条件;
充要条件
知识点二
充要条件
充分、必要条件的四种类型——逻辑关系
1、从逻辑推理关系看充分条件、必要条件:
1)若p q但q p,则p是q的充分非必要条件
2)若p q但q p,则p是q的必要非充分条件
3)若p q且q p,则p是q的充要条件
4)若p q且q p, 则p是q的既不充分也不必要条件
充分、必要条件的四种类型
充分、必要条件的四种类型——集合与集合的关系
2、从集合与集合的关系看充分条件、必要条件
p;A={x|x满足条件p} q; B={x|x满足条件q}
1)若A?B且B? A,则p是q的充分非必要条件
2)若A?B且B?A,则p是q的必要非充分条件
3)若A?B且B? A,则p是q的既不充分也不必要条件
4)若A=B ,则p是q的充要条件
充分、必要条件的四种类型
例题3.用“充分不必要”“必要不充分”“充要”“既不充分也不必要”填空:
(1)“x2=4”是“x=-2”的 条件;?
(2)“二次函数y=ax2开口向上”是“a>0 ”的 条件;?
(4)“x为正数,y为负数”是“x-y>0”的 条件.?
必要不充分
充要
充分不必要
典型例题——必要条件
随堂练习
1.“-21或x<-1”的( )
A.充分条件但不是必要条件
B.必要条件但不是充分条件
C.既不是充分条件,也不是必要条件
D.既是充分条件,也是必要条件
C
随堂练习
2.下列命题中,真命题是 ( )
A.“x2>0”是“x>0”的充分条件
B.“xy=0”是“x=0”的必要条件
C.“|a|=|b|”是“a=b”的充分条件
D.“|x|>1”是“x2不小于1”的必要条件
D
随堂练习
3.设计如下图所示的两个电路图,条件A:“开关S1闭合”;条件B:“灯泡L亮”,问A是B的什么条件?
解:对于图甲,开关S1闭合灯亮,反过来灯泡L亮,也可能是开关S2闭合,所以A是B的充分不必要条件;
对于图乙,所以灯亮必须S1和S2同时闭合,
所以A是B的必要不充分条件。
随堂练习
4.求证:一元二次方程ax2+bx+c=0有一个正根和一个负根的充要条件是ac<0.
证明(充分性)因为ac<0,所以一元二次方程ax2+bx+c=0的判别式Δ=b2-4ac>0,
故一元二次方程一定有两个不等实根,设为x1,x2,则x1x2= <0,
所以一元二次方程的两根异号.
即一元二次方程ax2+bx+c=0有一个正根和一个负根.
(必要性)由于一元二次方程有一个正根和一个负根,设为x1,x2,
则由根与系数的关系,得x1x2= <0,即ac<0.
综上可知,一元二次方程ax2+bx+c=0有一个正根和一个负根的充要条件是ac<0.
课堂小结
1.命题真假的判断
2.充分条件与必要条件的定义与判断
3.充要条件的定义与判断
4.从集合的角度理解充分条件与必要条件
1.4.1 充分条件与必要条件
教学目标
1.知识与技能
理解充分条件、必要条件的定义;会判断条件与结论的关系,会判断命题的充分条件、必要条件.
2.过程与方法
通过判断p与q的关系引导充要条件的定义,由诱导探究的方法归纳出判断“p是q的什么条件”步骤及方法.
3.情感、态度与价值观
让学生通过练题总结归纳,培养学生理解、分析、归纳、解决问题的能力;从实际例子体会数学的有用性,“在生活中数学地思维”,增强对数学逻辑知识的兴趣,激发学生的数学兴趣。
重点难点
[重点]
1.充分条件、必要条件、充要条件的概念;
2.充分条件、必要条件与判定定理、性质定理的关系.
[难点]
命题的充分条件、必要条件的判断;
充要条件的理解与判断。
并 集
一般地,由所有属于集合A或属于集合B的元素组成的集合,称为集合A与B的并集,记作 A∪B,读作“A并B”。
即 A∪B={x | x∈A,或x∈B}
温故知新
交 集
一般地,由既属于集合A又属于集合B的所有元素组成的集合,称为A与B的交集.记作 A∩B,读作“A交B”. 即 A∩B={x|x∈A,且x∈B}
温故知新
补 集
对于一个集合A,由全集U中不属于A的所有元素组成的集合称为集合A相对于全集U的补集,简称为集合A的补集,记作CuA.即CuA ={x|x∈U,且x?A}
温故知新
新课导入
在初中,我们对命题已经有了初步的认识。
一般地,我们把用语言、符号或式子表达的, 可以判断真假的陈述句叫做命题。 其中,
判断为真的命题叫真命题;
判断为假的命题叫假命题。
很多命题可以写成“若 p ,则 q ”或“如果 p ,那么 q ”
“若 p ,则 q ”形式的命题中的 p 称为命题的条件, q 称为命题的结论。
问题思考
思考?
指出下列两个命题的条件和结论,并判断是真命题还是假命题?
(1)若a2=b2,则a=b;
(2)若ab=0,则a=0或b=0;
命题(1)为假命题,条件:a2=b2,结论a=b。
命题(2)为真命题.条件:ab=0,结论a=0或b=0。
充分条件与必要条件定义
知识点一
充分条件与必要条件定义
一般地,“若p,则q”为真命题,是指由p通过推理可以得出q.这时,我们就说,由p可推出q,记作:
p?q.
定义:如果命题“若p,则q”为真命题,即p?q,那么我们就说p是q的充分条件;q是p必要条件.
典型例题——充分条件
解:(1)(3)为真命题,(2)是假命题,
所以(1)(3)的p是q的充分条件;
典型例题——必要条件
解:(2)(3)为真命题,(1)是假命题,
所以(2)(3)的p是q的充分条件;
充要条件
知识点二
充要条件
充分、必要条件的四种类型——逻辑关系
1、从逻辑推理关系看充分条件、必要条件:
1)若p q但q p,则p是q的充分非必要条件
2)若p q但q p,则p是q的必要非充分条件
3)若p q且q p,则p是q的充要条件
4)若p q且q p, 则p是q的既不充分也不必要条件
充分、必要条件的四种类型
充分、必要条件的四种类型——集合与集合的关系
2、从集合与集合的关系看充分条件、必要条件
p;A={x|x满足条件p} q; B={x|x满足条件q}
1)若A?B且B? A,则p是q的充分非必要条件
2)若A?B且B?A,则p是q的必要非充分条件
3)若A?B且B? A,则p是q的既不充分也不必要条件
4)若A=B ,则p是q的充要条件
充分、必要条件的四种类型
例题3.用“充分不必要”“必要不充分”“充要”“既不充分也不必要”填空:
(1)“x2=4”是“x=-2”的 条件;?
(2)“二次函数y=ax2开口向上”是“a>0 ”的 条件;?
(4)“x为正数,y为负数”是“x-y>0”的 条件.?
必要不充分
充要
充分不必要
典型例题——必要条件
随堂练习
1.“-2
A.充分条件但不是必要条件
B.必要条件但不是充分条件
C.既不是充分条件,也不是必要条件
D.既是充分条件,也是必要条件
C
随堂练习
2.下列命题中,真命题是 ( )
A.“x2>0”是“x>0”的充分条件
B.“xy=0”是“x=0”的必要条件
C.“|a|=|b|”是“a=b”的充分条件
D.“|x|>1”是“x2不小于1”的必要条件
D
随堂练习
3.设计如下图所示的两个电路图,条件A:“开关S1闭合”;条件B:“灯泡L亮”,问A是B的什么条件?
解:对于图甲,开关S1闭合灯亮,反过来灯泡L亮,也可能是开关S2闭合,所以A是B的充分不必要条件;
对于图乙,所以灯亮必须S1和S2同时闭合,
所以A是B的必要不充分条件。
随堂练习
4.求证:一元二次方程ax2+bx+c=0有一个正根和一个负根的充要条件是ac<0.
证明(充分性)因为ac<0,所以一元二次方程ax2+bx+c=0的判别式Δ=b2-4ac>0,
故一元二次方程一定有两个不等实根,设为x1,x2,则x1x2= <0,
所以一元二次方程的两根异号.
即一元二次方程ax2+bx+c=0有一个正根和一个负根.
(必要性)由于一元二次方程有一个正根和一个负根,设为x1,x2,
则由根与系数的关系,得x1x2= <0,即ac<0.
综上可知,一元二次方程ax2+bx+c=0有一个正根和一个负根的充要条件是ac<0.
课堂小结
1.命题真假的判断
2.充分条件与必要条件的定义与判断
3.充要条件的定义与判断
4.从集合的角度理解充分条件与必要条件
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
