2.2 基本不等式 课件(共23张PPT)
文档属性
| 名称 | 2.2 基本不等式 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 214.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-02 12:09:49 | ||
图片预览






文档简介
第一章 集合与常用逻辑用语
2.2 基本不等式
教学目标
1、理解基本不等式的定义;
2、掌握基本不等式的证明;
3、了解基本不等式的几何解释;
4、运用基本不等式求最值
5、结合具体实例,用基本不等式解决简单的求最大值或最小值的问题,发展数学运算和数学建模素养.
6、在猜想论证的过程中,体会数学的严谨性。
重点难点
重点
1、基本不等式的定义及推导
2、运用基本不等式解决简单的最值问题.
难点
基本不等式的证明和运用基本不等式求最值.
温故知新
知识点一 不等关系的表示
不等关系
a大于b
a小于b
a不大于b
a不小于b
a不等于b
符号表示
a ????b
a ????b
a ??? ????b
a ???? ????b
a ????????b
>
<
≤
≥
≠
温故知新
知识点二 不等式的基本事实
a>b?????a-b>0????;
a=b?????a-b=0????;
a温故知新
知识点三 等式的基本性质
温故知新
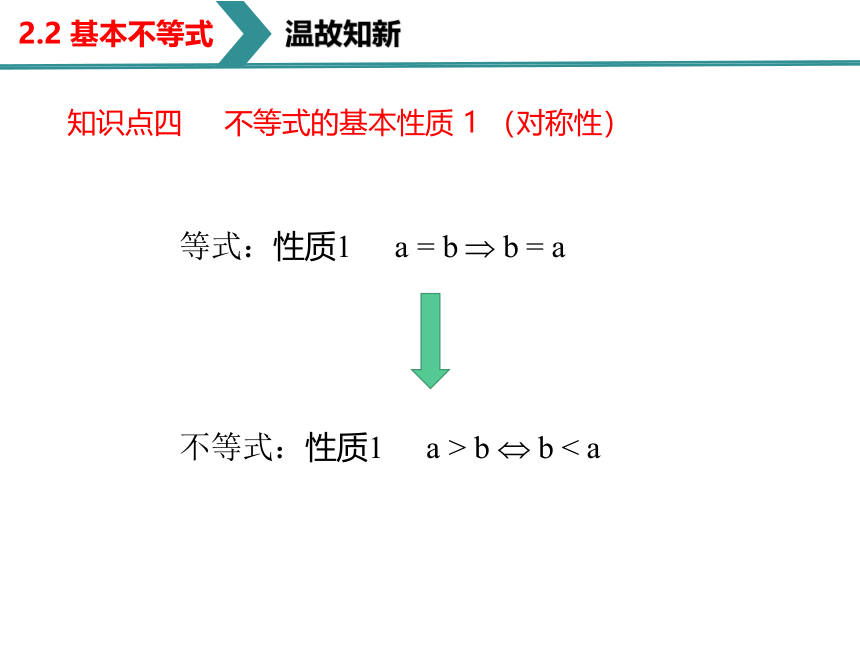
知识点四 不等式的基本性质 1 (对称性)
温故知新
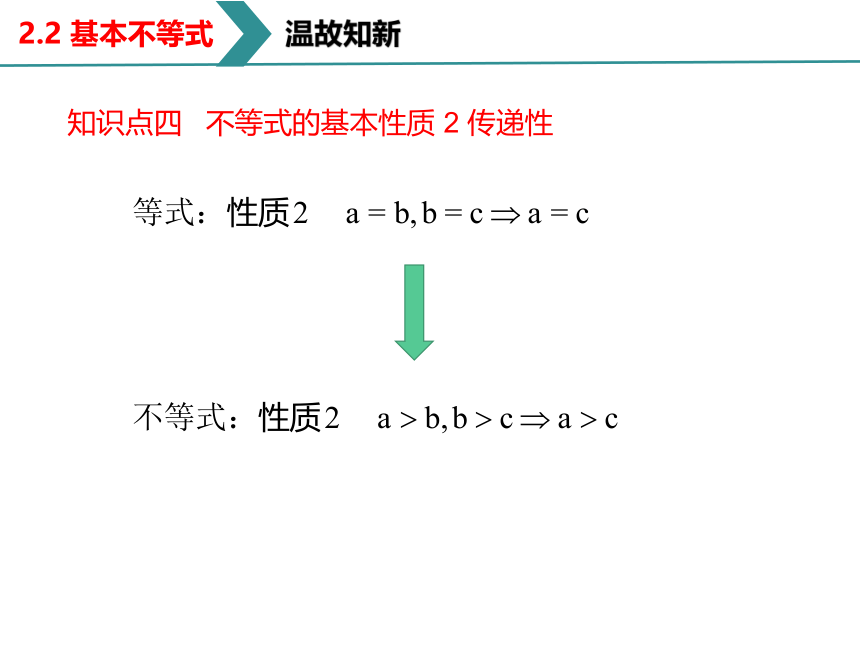
知识点四 不等式的基本性质 2 传递性
温故知新
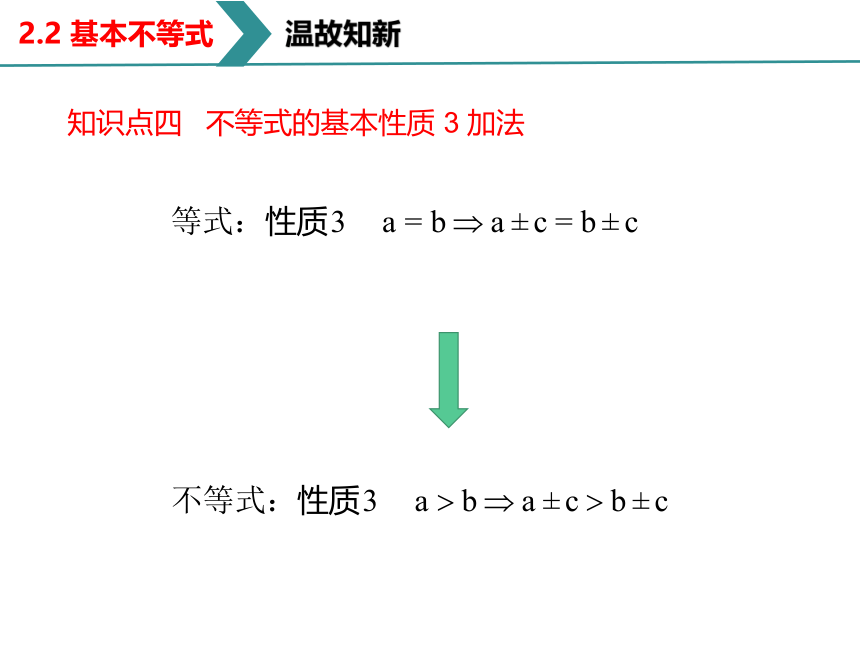
知识点四 不等式的基本性质 3 加法
温故知新
知识点四 不等式的基本性质4 乘法
温故知新
知识点四 不等式的基本性质
性质5
a>b,c>d??????a+c>b+d????
性质6
a>b>0,c>d>0?????ac>bd???
性质7
a>b>0??????an>bn????(n∈N,n≥2)
新课导入
思考
提到两个数的乘法,在上一节(P39探究)我们利用完全平方差公式得出了一类重要不等式中含有ab乘法,是什么不等式?
a2+b2≥ 2ab????
当且仅当②????a=b????时,等号成立
新课导入
思考
提到两个数的乘法,在上一节(P39探究)我们利用完全平方差公式得出了一类重要不等式中含有ab乘法,是什么不等式?
a2+b2≥ 2ab????
当且仅当????a=b????时,等号成立
新课导入
知识点一 基本不等式
? ≤
当且仅当a=b?时,等号成立(a>0,b>0)
叫a,b的几何平均数, 叫a,b的算术平均数
经典例题
1、“a,b为正数”是“ ”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
D
提示:没有取等
经典例题
2、若a,b∈R,且ab>0,则下列不等式恒成立的是( )
D
随堂练习
1、设0A. B.a2+b2 C.2ab D.a
B
随堂练习
随堂练习
3、某人要用铁管做一个形状为直角三角形且面积为1 m2的铁架框(铁管的粗细忽略不计),在下面四种长度的铁管中,最合理(够用,又浪费最少)的是( )
A.4.6 m B.4.8 m C.5 m D.5.2 m
随堂练习
3、某人要用铁管做一个形状为直角三角形且面积为1 m2的铁架框(铁管的粗细忽略不计),在下面四种长度的铁管中,最合理(够用,又浪费最少)的是( )
A.4.6 m B.4.8 m C.5 m D.5.2 m
随堂练习
4、若正数x,y满足x+4y-xy=0,则当x+y取得最小值时,x的值为( )
A.9 B.8 C.6 D.3
C
课堂小结
1、a2+b2≥ 2ab?,当且仅当????a=b????时,等号成立
2、 ≤
当且仅当a=b?时,等号成立(a>0,b>0)
2.2 基本不等式
教学目标
1、理解基本不等式的定义;
2、掌握基本不等式的证明;
3、了解基本不等式的几何解释;
4、运用基本不等式求最值
5、结合具体实例,用基本不等式解决简单的求最大值或最小值的问题,发展数学运算和数学建模素养.
6、在猜想论证的过程中,体会数学的严谨性。
重点难点
重点
1、基本不等式的定义及推导
2、运用基本不等式解决简单的最值问题.
难点
基本不等式的证明和运用基本不等式求最值.
温故知新
知识点一 不等关系的表示
不等关系
a大于b
a小于b
a不大于b
a不小于b
a不等于b
符号表示
a ????b
a ????b
a ??? ????b
a ???? ????b
a ????????b
>
<
≤
≥
≠
温故知新
知识点二 不等式的基本事实
a>b?????a-b>0????;
a=b?????a-b=0????;
a
知识点三 等式的基本性质
温故知新
知识点四 不等式的基本性质 1 (对称性)
温故知新
知识点四 不等式的基本性质 2 传递性
温故知新
知识点四 不等式的基本性质 3 加法
温故知新
知识点四 不等式的基本性质4 乘法
温故知新
知识点四 不等式的基本性质
性质5
a>b,c>d??????a+c>b+d????
性质6
a>b>0,c>d>0?????ac>bd???
性质7
a>b>0??????an>bn????(n∈N,n≥2)
新课导入
思考
提到两个数的乘法,在上一节(P39探究)我们利用完全平方差公式得出了一类重要不等式中含有ab乘法,是什么不等式?
a2+b2≥ 2ab????
当且仅当②????a=b????时,等号成立
新课导入
思考
提到两个数的乘法,在上一节(P39探究)我们利用完全平方差公式得出了一类重要不等式中含有ab乘法,是什么不等式?
a2+b2≥ 2ab????
当且仅当????a=b????时,等号成立
新课导入
知识点一 基本不等式
? ≤
当且仅当a=b?时,等号成立(a>0,b>0)
叫a,b的几何平均数, 叫a,b的算术平均数
经典例题
1、“a,b为正数”是“ ”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
D
提示:没有取等
经典例题
2、若a,b∈R,且ab>0,则下列不等式恒成立的是( )
D
随堂练习
1、设0
B
随堂练习
随堂练习
3、某人要用铁管做一个形状为直角三角形且面积为1 m2的铁架框(铁管的粗细忽略不计),在下面四种长度的铁管中,最合理(够用,又浪费最少)的是( )
A.4.6 m B.4.8 m C.5 m D.5.2 m
随堂练习
3、某人要用铁管做一个形状为直角三角形且面积为1 m2的铁架框(铁管的粗细忽略不计),在下面四种长度的铁管中,最合理(够用,又浪费最少)的是( )
A.4.6 m B.4.8 m C.5 m D.5.2 m
随堂练习
4、若正数x,y满足x+4y-xy=0,则当x+y取得最小值时,x的值为( )
A.9 B.8 C.6 D.3
C
课堂小结
1、a2+b2≥ 2ab?,当且仅当????a=b????时,等号成立
2、 ≤
当且仅当a=b?时,等号成立(a>0,b>0)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
