3.1 函数的概念1函数的概念及表示 课件(共22张PPT)
文档属性
| 名称 | 3.1 函数的概念1函数的概念及表示 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 294.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-02 13:40:52 | ||
图片预览






文档简介
第三章 函数概念与性质
3.1 函数的概念
(第一课时)
教学目标
1.了解构成函数的要素,会求一些简单函数的定义域和值域;了解映射的概念;
2.会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数;
3.通过具体实例,了解简单的分段函数,并能简单应用;
4.学会运用函数图象理解和研究函数的性质。
重点难点
重点:
函数的基本定义及表示
难点:
函数的定义域、值域和对应关系
新课导入
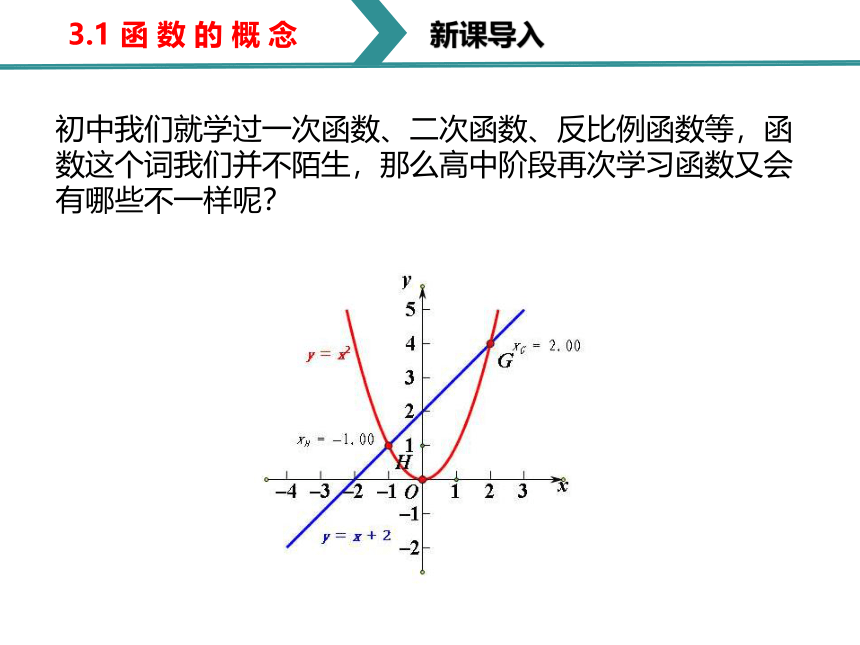
初中我们就学过一次函数、二次函数、反比例函数等,函数这个词我们并不陌生,那么高中阶段再次学习函数又会有哪些不一样呢?
问题1
(1)某高速列车加速到300 kmh后保持匀速运行半小时.这段时间内,列车行进的路程S(单位:km)与运行时间t(单位:h)的关系可以表示为
S=300t.
这里,t和S是两个变量,而且对于t的每一个确定的值,S都有唯一确定的值与之对应,所以S是t的函数.
新课导入
问题2
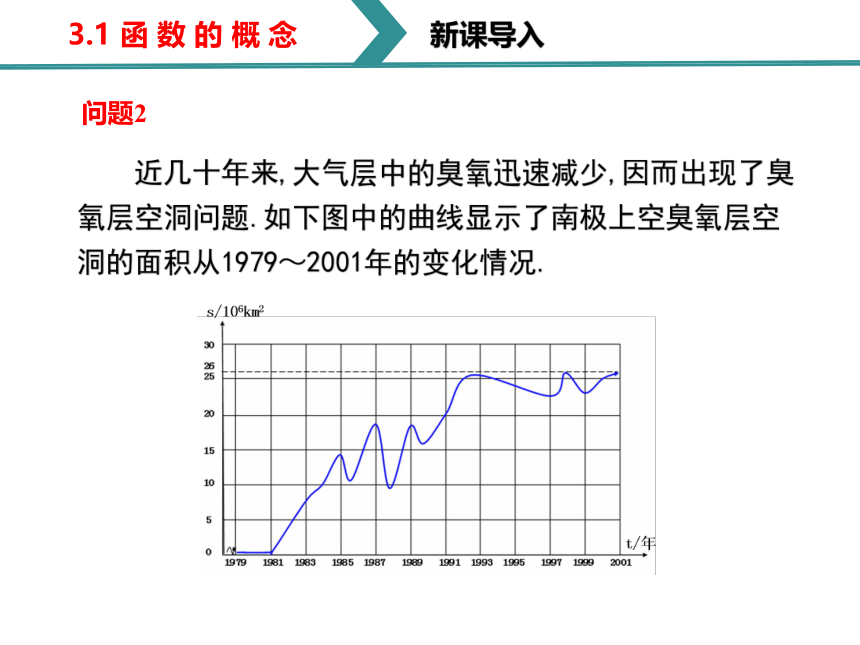
近几十年来,大气层中的臭氧迅速减少,因而出现了臭氧层空洞问题.如下图中的曲线显示了南极上空臭氧层空洞的面积从1979~2001年的变化情况.
新课导入
问题3
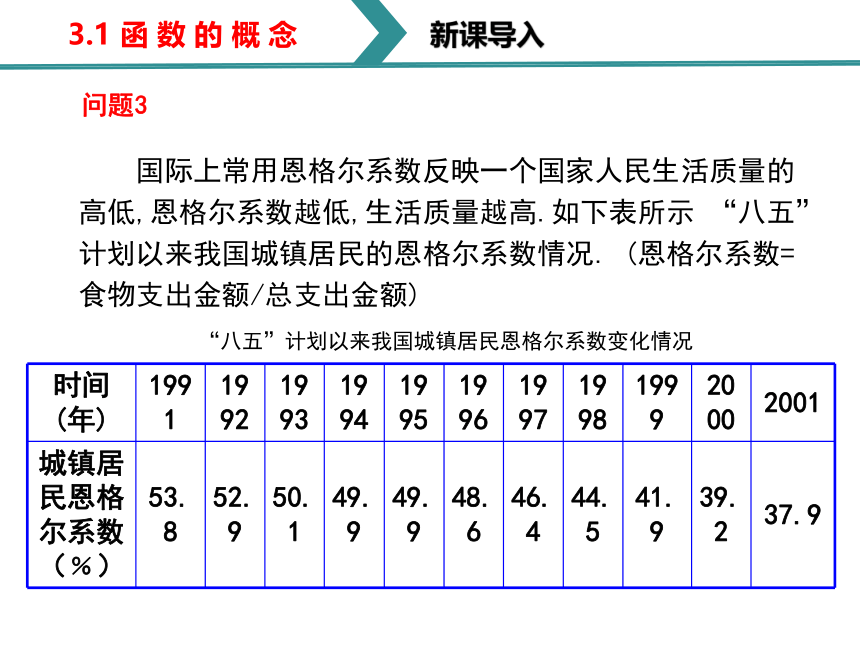
国际上常用恩格尔系数反映一个国家人民生活质量的高低,恩格尔系数越低,生活质量越高.如下表所示 “八五”计划以来我国城镇居民的恩格尔系数情况. (恩格尔系数=食物支出金额/总支出金额)
时间(年)
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
城镇居民恩格尔系数(﹪)
53.8
52.9
50.1
49.9
49.9
48.6
46.4
44.5
41.9
39.2
37.9
“八五”计划以来我国城镇居民恩格尔系数变化情况
新课导入
(1)实例1、2、3有什么不同点?
新课导入
变量间的对应方式不同,1是关系式,2是图像,3是表格
(2)以上3个实例有什么共同点?
(1)都有两个非空数集.
(2)两个数集之间都有一种确定的对应关系.
知识点一 函数的定义
设A、B都是非空的数集,如果按某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数 f(x)和它对应,那么就称f:A→B为集合A到集合B的一个函数。
记作y=f(x). x∈A
其中x叫做自变量,
x的取值范围A叫做函数y=f(x)的定义域,
与x的值相对应的y的值叫做函数值,
函数值的集合C = { f(x)| x∈A }
叫做函数的值域。
函数的定义
函数的定义
(1)A,B为非空数集
(2)任意——唯一
(3)一对一,多对一(不能一对多)
(4)对应关系可以有解析式,图像,表 格
知识点一 函数的定义
注意
函数的定义
值域由对应关系f与定义域确定
所以判定两函数是否相同
只需定义域与对应关系相同即可
知识点一 函数的定义
(1)函数符号y=f(x)表示“y是x的函数”。
(2)定义中与x对应的数用f(x)表示,f(x)不是f与x 的乘积,表示的是x经f变化后对应的函数值。所以若对应关系用g、 G、F 等表示,则函数就可用g(x)、F(x)、G(x)等 表示。
(3)集合A、B与f一起称A到B的函数,而非对应关系f或集合A、B叫函数。
(4)函数的三要素,定义域,对应关系f,值域。
例1.?正比例函数y=kx(k≠0)可以用来刻画匀速运动中的路程与时间的关系、一定密度的物体的质量与体积的关系、圆的周长与半径的关系等。试构建一个问题情境,使其中的变量关系可以用解析式y=x(10-x)来描述。
解:把y=x(10-x)看成二次函数,那么它的定义域是R,值域是B={y|y≤25}.对应关系f:R→B,使得R中的任意一个数x与B中的数x(10-x)相对应.
如果对x的取值范围作出限制,例如x∈{x|0<x<10} ,那么可以构建如下情境:
长方形的边长之和为20,设一边长为x,面积为y,那么y=x(10-x).其中,x的取值范围是A={x|0<x<10},y的取值范围是B={y|0<y≤25}.对应关系f:A→B使长方形的边长x与它的面积x(10-x)相对应.
典型例题
例2 求 的定义域
解:定义域:x-2≠0,则x≠2
∴定义域:{x|x≠2}
典型例题
例3 已知函数
(1)求函数的定义域.(2)求 的值.
(3)当a>0时,求f(a),f(a-1)的值.
典型例题
1、函数y=f(x)的图象与直线x=a(a∈R)的交点( )
A.至多有一个
B.至少有一个
C.有且仅有一个
D.有两个以上
随堂练习
A
2、下列各图中,可表示函数y=f(x)的图象的是( )
随堂练习
D
3、已知函数f(x)=ax2-1,a为正数,且f(f(-1))=-1,那么a的值是( )
A.1 B.0 C.-1 D.2
随堂练习
A
解:∵f(x)=ax2-1,
∴f(-1)=a-1,f(f(-1))=f(a-1)=a·(a-1)2-1=-1,
∴a(a-1)2=0.
又∵a为正数,
∴a=1.
随堂练习
4、已知函数f(x)=11+x(x∈R,且x≠-1),g(x)=x2+2(x∈R).
(1)求f(2),g(2)的值;
(2)求f(g(3))的值;
(3)若f(g(x))=14,求x的值.
随堂练习
4、已知函数f(x)=11+x(x∈R,且x≠-1),g(x)=x2+2(x∈R).
(1)求f(2),g(2)的值;
(2)求f(g(3))的值;
解(1)f(2)=11+2=13.
g(2)=22+2=6.
(2)g(3)=32+2=11,
∴f(g(3))=f(11)=11+11=22.
随堂练习
4、已知函数f(x)=11+x(x∈R,且x≠-1),g(x)=x2+2(x∈R).
(3)若f(g(x))=14,求x的值.
(3)解法一:∵f(g(x))=14,
∴11+g(x)=14,
解得g(x)=3,
∴x2+2=3,解得x=±1.
解法二:∵f(g(x))=f(x2+2)
=11+x2+2=13+x2,
∴13+x2=14,∴x2=1,解得x=±1.
课堂小结
函数的概念及其表示
{5940675A-B579-460E-94D1-54222C63F5DA}函数
一般地,设A,B是非空的实数集,如果对于集合A中的任意一个数x,按照某种确定的对应关系f,在集合B中都有唯一确定的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数
表示法
解析法、列表法和图象法
3.1 函数的概念
(第一课时)
教学目标
1.了解构成函数的要素,会求一些简单函数的定义域和值域;了解映射的概念;
2.会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数;
3.通过具体实例,了解简单的分段函数,并能简单应用;
4.学会运用函数图象理解和研究函数的性质。
重点难点
重点:
函数的基本定义及表示
难点:
函数的定义域、值域和对应关系
新课导入
初中我们就学过一次函数、二次函数、反比例函数等,函数这个词我们并不陌生,那么高中阶段再次学习函数又会有哪些不一样呢?
问题1
(1)某高速列车加速到300 kmh后保持匀速运行半小时.这段时间内,列车行进的路程S(单位:km)与运行时间t(单位:h)的关系可以表示为
S=300t.
这里,t和S是两个变量,而且对于t的每一个确定的值,S都有唯一确定的值与之对应,所以S是t的函数.
新课导入
问题2
近几十年来,大气层中的臭氧迅速减少,因而出现了臭氧层空洞问题.如下图中的曲线显示了南极上空臭氧层空洞的面积从1979~2001年的变化情况.
新课导入
问题3
国际上常用恩格尔系数反映一个国家人民生活质量的高低,恩格尔系数越低,生活质量越高.如下表所示 “八五”计划以来我国城镇居民的恩格尔系数情况. (恩格尔系数=食物支出金额/总支出金额)
时间(年)
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
城镇居民恩格尔系数(﹪)
53.8
52.9
50.1
49.9
49.9
48.6
46.4
44.5
41.9
39.2
37.9
“八五”计划以来我国城镇居民恩格尔系数变化情况
新课导入
(1)实例1、2、3有什么不同点?
新课导入
变量间的对应方式不同,1是关系式,2是图像,3是表格
(2)以上3个实例有什么共同点?
(1)都有两个非空数集.
(2)两个数集之间都有一种确定的对应关系.
知识点一 函数的定义
设A、B都是非空的数集,如果按某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数 f(x)和它对应,那么就称f:A→B为集合A到集合B的一个函数。
记作y=f(x). x∈A
其中x叫做自变量,
x的取值范围A叫做函数y=f(x)的定义域,
与x的值相对应的y的值叫做函数值,
函数值的集合C = { f(x)| x∈A }
叫做函数的值域。
函数的定义
函数的定义
(1)A,B为非空数集
(2)任意——唯一
(3)一对一,多对一(不能一对多)
(4)对应关系可以有解析式,图像,表 格
知识点一 函数的定义
注意
函数的定义
值域由对应关系f与定义域确定
所以判定两函数是否相同
只需定义域与对应关系相同即可
知识点一 函数的定义
(1)函数符号y=f(x)表示“y是x的函数”。
(2)定义中与x对应的数用f(x)表示,f(x)不是f与x 的乘积,表示的是x经f变化后对应的函数值。所以若对应关系用g、 G、F 等表示,则函数就可用g(x)、F(x)、G(x)等 表示。
(3)集合A、B与f一起称A到B的函数,而非对应关系f或集合A、B叫函数。
(4)函数的三要素,定义域,对应关系f,值域。
例1.?正比例函数y=kx(k≠0)可以用来刻画匀速运动中的路程与时间的关系、一定密度的物体的质量与体积的关系、圆的周长与半径的关系等。试构建一个问题情境,使其中的变量关系可以用解析式y=x(10-x)来描述。
解:把y=x(10-x)看成二次函数,那么它的定义域是R,值域是B={y|y≤25}.对应关系f:R→B,使得R中的任意一个数x与B中的数x(10-x)相对应.
如果对x的取值范围作出限制,例如x∈{x|0<x<10} ,那么可以构建如下情境:
长方形的边长之和为20,设一边长为x,面积为y,那么y=x(10-x).其中,x的取值范围是A={x|0<x<10},y的取值范围是B={y|0<y≤25}.对应关系f:A→B使长方形的边长x与它的面积x(10-x)相对应.
典型例题
例2 求 的定义域
解:定义域:x-2≠0,则x≠2
∴定义域:{x|x≠2}
典型例题
例3 已知函数
(1)求函数的定义域.(2)求 的值.
(3)当a>0时,求f(a),f(a-1)的值.
典型例题
1、函数y=f(x)的图象与直线x=a(a∈R)的交点( )
A.至多有一个
B.至少有一个
C.有且仅有一个
D.有两个以上
随堂练习
A
2、下列各图中,可表示函数y=f(x)的图象的是( )
随堂练习
D
3、已知函数f(x)=ax2-1,a为正数,且f(f(-1))=-1,那么a的值是( )
A.1 B.0 C.-1 D.2
随堂练习
A
解:∵f(x)=ax2-1,
∴f(-1)=a-1,f(f(-1))=f(a-1)=a·(a-1)2-1=-1,
∴a(a-1)2=0.
又∵a为正数,
∴a=1.
随堂练习
4、已知函数f(x)=11+x(x∈R,且x≠-1),g(x)=x2+2(x∈R).
(1)求f(2),g(2)的值;
(2)求f(g(3))的值;
(3)若f(g(x))=14,求x的值.
随堂练习
4、已知函数f(x)=11+x(x∈R,且x≠-1),g(x)=x2+2(x∈R).
(1)求f(2),g(2)的值;
(2)求f(g(3))的值;
解(1)f(2)=11+2=13.
g(2)=22+2=6.
(2)g(3)=32+2=11,
∴f(g(3))=f(11)=11+11=22.
随堂练习
4、已知函数f(x)=11+x(x∈R,且x≠-1),g(x)=x2+2(x∈R).
(3)若f(g(x))=14,求x的值.
(3)解法一:∵f(g(x))=14,
∴11+g(x)=14,
解得g(x)=3,
∴x2+2=3,解得x=±1.
解法二:∵f(g(x))=f(x2+2)
=11+x2+2=13+x2,
∴13+x2=14,∴x2=1,解得x=±1.
课堂小结
函数的概念及其表示
{5940675A-B579-460E-94D1-54222C63F5DA}函数
一般地,设A,B是非空的实数集,如果对于集合A中的任意一个数x,按照某种确定的对应关系f,在集合B中都有唯一确定的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数
表示法
解析法、列表法和图象法
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
