3.1 函数的概念2区间的概念及表示 课件(共23张PPT)
文档属性
| 名称 | 3.1 函数的概念2区间的概念及表示 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 245.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-02 13:46:13 | ||
图片预览








文档简介
第三章 函数概念与性质
3.1 函数的概念
(第二课时)
教学目标
(1)?理解区间的概念,掌握用区间表示不等式解集的方法,并能在数轴上表示出来。
(2).通过教学,渗透数形结合的思想和由一般到特殊的辩证唯物主义观点。
(3).培养学生合作交流的意识和乐于探究的良好思维品质,让学生从数学学习活动中获得成功的体验,树立自信心。
重点难点
重点:
用区间表示数集.
?
难点:
对无穷区间的理解.
知识点一 函数的定义
设A、B都是非空的数集,如果按某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数 f(x)和它对应,那么就称f:A→B为集合A到集合B的一个函数。
记作y=f(x). x∈A
其中x叫做自变量,
x的取值范围A叫做函数y=f(x)的定义域,
与x的值相对应的y的值叫做函数值,
函数值的集合C = { f(x)| x∈A }
叫做函数的值域。
温故知新
(1)A,B为非空数集
(2)任意——唯一
(3)一对一,多对一(不能一对多)
(4)对应关系可以有解析式,图像,表 格
知识点一 函数的定义
注意
温故知新
值域由对应关系f与定义域确定
所以判定两函数是否相同
只需定义域与对应关系相同即可
知识点一 函数的定义
(1)函数符号y=f(x)表示“y是x的函数”。
(2)定义中与x对应的数用f(x)表示,f(x)不是f与x 的乘积,表示的是x经f变化后对应的函数值。所以若对应关系用g、 G、F 等表示,则函数就可用g(x)、F(x)、G(x)等 表示。
(3)集合A、B与f一起称A到B的函数,而非对应关系f或集合A、B叫函数。
(4)函数的三要素,定义域,对应关系f,值域。
温故知新
温故知新
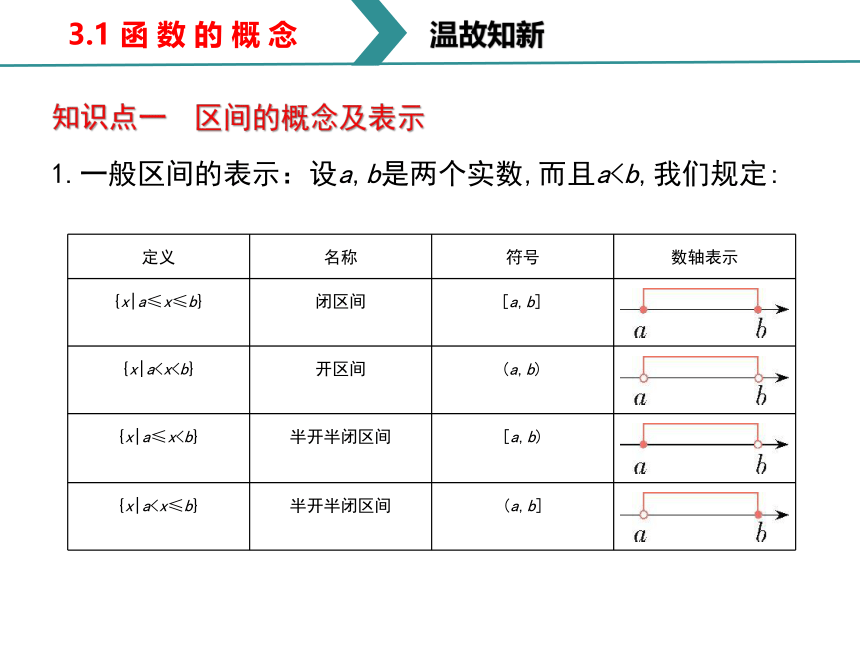
1.一般区间的表示:设a,b是两个实数,而且a定义
名称
符号
数轴表示
{x|a≤x≤b}
闭区间
[a,b]????
?
{x|a开区间
(a,b)????
?
{x|a≤x半开半闭区间
[a,b)
?
{x|a半开半闭区间
(a,b]
?
知识点一 区间的概念及表示
典型例题
解:(1) 有意义的实数x的集合是{x|x≥-3}
有意义的实数x的集合是{x|x≠-2}
∴定义域就是 .
(2)
例1 已知函数
(1)求函数的定义域.(2)求 的值.
例3 已知函数
(3)当a>0时,求f(a),f(a-1)的值.
(3)因为a>0,所以f(a),f(a-1)有意义.
典型例题
典型例题
例2 下列函数中哪个与函数y=x相等( )
A. B.
C. D.
B
随堂练习
1、试用区间表示下列实数集
(1){x|2≤x<3}
(2){x|x≥15}
(3){x|x≤0}∩{x|-3 ≤x<8}
(4){x|x<-10}∪{x|3随堂练习
2.(2020河南洛阳一高高一上月考)
若函数 的定义域为M, 的定义域为N,求M∩N
随堂练习
3.已知函数y=f(x)的图象如图所示,则该函数的值域为 . ?
[-4,3].
随堂练习
随堂练习
随堂练习
4.已知函数f(x)的定义域为[1,3],求函数f(2x+1)的定义域;
解:由题意知,函数f(2x+1)中2x+1的范围与函数f(x)中x的范围相同,
∵x∈[1,3],∴2x+1∈[1,3],即x∈[0,1],
∴函数f(2x+1)的定义域为[0,1].
随堂练习
5.已知函数f(2x+1)的定义域为[1,3],求函数f(x)的定义域;
解:∵x∈[1,3]
∴2x+1∈[3,7]
∴函数f(x)的定义域为[3,7].
随堂练习
6.已知函数f(2x+1)的定义域为[1,3],
求函数f(3x)的定义域;
解:∵x∈[1,3],
∴2x+1∈[3,7],
∴3x∈[3,7],即x∈?,
∴函数f(3x)的定义域为 ?.
随堂练习
7.已知函数f(x)=11+x(x∈R,且x≠-1),g(x)=x2+2(x∈R).
(1)求f(2),g(2)的值;
(2)求f(g(3))的值;
(3)若f(g(x))=14,求x的值.
解:(1)
f(2)=11+2=13,
g(2)=22+2=6.
随堂练习
7.已知函数f(x)=11+x(x∈R,且x≠-1),g(x)=x2+2(x∈R).
(1)求f(2),g(2)的值;
(2)求f(g(3))的值;
(3)若f(g(x))=14,求x的值.
(2)g(3)=32+2=11,
∴f(g(3))=f(11)=11+11=22.
随堂练习
7.已知函数f(x)=11+x(x∈R,且x≠-1),g(x)=x2+2(x∈R).
(1)求f(2),g(2)的值;
(2)求f(g(3))的值;
(3)若f(g(x))=14,求x的值.
(3)解法一:∵f(g(x))=14,
∴11+g(x)=14,解得g(x)=3,
∴x2+2=3,解得x=±1.
解法二:∵f(g(x))=f(x2+2)
=11+x2+2=13+x2,
∴13+x2=14,∴x2=1,解得x=±1.
课堂小结
1.函数的定义
2.区间的概念
3.区间的表示
3.1 函数的概念
(第二课时)
教学目标
(1)?理解区间的概念,掌握用区间表示不等式解集的方法,并能在数轴上表示出来。
(2).通过教学,渗透数形结合的思想和由一般到特殊的辩证唯物主义观点。
(3).培养学生合作交流的意识和乐于探究的良好思维品质,让学生从数学学习活动中获得成功的体验,树立自信心。
重点难点
重点:
用区间表示数集.
?
难点:
对无穷区间的理解.
知识点一 函数的定义
设A、B都是非空的数集,如果按某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数 f(x)和它对应,那么就称f:A→B为集合A到集合B的一个函数。
记作y=f(x). x∈A
其中x叫做自变量,
x的取值范围A叫做函数y=f(x)的定义域,
与x的值相对应的y的值叫做函数值,
函数值的集合C = { f(x)| x∈A }
叫做函数的值域。
温故知新
(1)A,B为非空数集
(2)任意——唯一
(3)一对一,多对一(不能一对多)
(4)对应关系可以有解析式,图像,表 格
知识点一 函数的定义
注意
温故知新
值域由对应关系f与定义域确定
所以判定两函数是否相同
只需定义域与对应关系相同即可
知识点一 函数的定义
(1)函数符号y=f(x)表示“y是x的函数”。
(2)定义中与x对应的数用f(x)表示,f(x)不是f与x 的乘积,表示的是x经f变化后对应的函数值。所以若对应关系用g、 G、F 等表示,则函数就可用g(x)、F(x)、G(x)等 表示。
(3)集合A、B与f一起称A到B的函数,而非对应关系f或集合A、B叫函数。
(4)函数的三要素,定义域,对应关系f,值域。
温故知新
温故知新
1.一般区间的表示:设a,b是两个实数,而且a
名称
符号
数轴表示
{x|a≤x≤b}
闭区间
[a,b]????
?
{x|a
(a,b)????
?
{x|a≤x
[a,b)
?
{x|a
(a,b]
?
知识点一 区间的概念及表示
典型例题
解:(1) 有意义的实数x的集合是{x|x≥-3}
有意义的实数x的集合是{x|x≠-2}
∴定义域就是 .
(2)
例1 已知函数
(1)求函数的定义域.(2)求 的值.
例3 已知函数
(3)当a>0时,求f(a),f(a-1)的值.
(3)因为a>0,所以f(a),f(a-1)有意义.
典型例题
典型例题
例2 下列函数中哪个与函数y=x相等( )
A. B.
C. D.
B
随堂练习
1、试用区间表示下列实数集
(1){x|2≤x<3}
(2){x|x≥15}
(3){x|x≤0}∩{x|-3 ≤x<8}
(4){x|x<-10}∪{x|3
2.(2020河南洛阳一高高一上月考)
若函数 的定义域为M, 的定义域为N,求M∩N
随堂练习
3.已知函数y=f(x)的图象如图所示,则该函数的值域为 . ?
[-4,3].
随堂练习
随堂练习
随堂练习
4.已知函数f(x)的定义域为[1,3],求函数f(2x+1)的定义域;
解:由题意知,函数f(2x+1)中2x+1的范围与函数f(x)中x的范围相同,
∵x∈[1,3],∴2x+1∈[1,3],即x∈[0,1],
∴函数f(2x+1)的定义域为[0,1].
随堂练习
5.已知函数f(2x+1)的定义域为[1,3],求函数f(x)的定义域;
解:∵x∈[1,3]
∴2x+1∈[3,7]
∴函数f(x)的定义域为[3,7].
随堂练习
6.已知函数f(2x+1)的定义域为[1,3],
求函数f(3x)的定义域;
解:∵x∈[1,3],
∴2x+1∈[3,7],
∴3x∈[3,7],即x∈?,
∴函数f(3x)的定义域为 ?.
随堂练习
7.已知函数f(x)=11+x(x∈R,且x≠-1),g(x)=x2+2(x∈R).
(1)求f(2),g(2)的值;
(2)求f(g(3))的值;
(3)若f(g(x))=14,求x的值.
解:(1)
f(2)=11+2=13,
g(2)=22+2=6.
随堂练习
7.已知函数f(x)=11+x(x∈R,且x≠-1),g(x)=x2+2(x∈R).
(1)求f(2),g(2)的值;
(2)求f(g(3))的值;
(3)若f(g(x))=14,求x的值.
(2)g(3)=32+2=11,
∴f(g(3))=f(11)=11+11=22.
随堂练习
7.已知函数f(x)=11+x(x∈R,且x≠-1),g(x)=x2+2(x∈R).
(1)求f(2),g(2)的值;
(2)求f(g(3))的值;
(3)若f(g(x))=14,求x的值.
(3)解法一:∵f(g(x))=14,
∴11+g(x)=14,解得g(x)=3,
∴x2+2=3,解得x=±1.
解法二:∵f(g(x))=f(x2+2)
=11+x2+2=13+x2,
∴13+x2=14,∴x2=1,解得x=±1.
课堂小结
1.函数的定义
2.区间的概念
3.区间的表示
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
