3.4 函数的应用 课件(共20张PPT)
文档属性
| 名称 | 3.4 函数的应用 课件(共20张PPT) |  | |
| 格式 | rar | ||
| 文件大小 | 394.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-02 17:03:24 | ||
图片预览





文档简介
第三章 函数概念与性质
3.4 函数的应用(一)
重点难点
重点:
运用一次函数、二次函数、幂函数、分段函数模型的处理实际问题;
难点:
运用函数思想理解和处理现实生活和社会中的简单问题.
温故知新
重点:
运用一次函数、二次函数、幂函数、分段函数模型的处理实际问题;
难点:
运用函数思想理解和处理现实生活和社会中的简单问题.
知识点一 幂函数的定义
一般地,函数y=xα叫做幂函数,其中x是自变量,α是常数.
温故知新
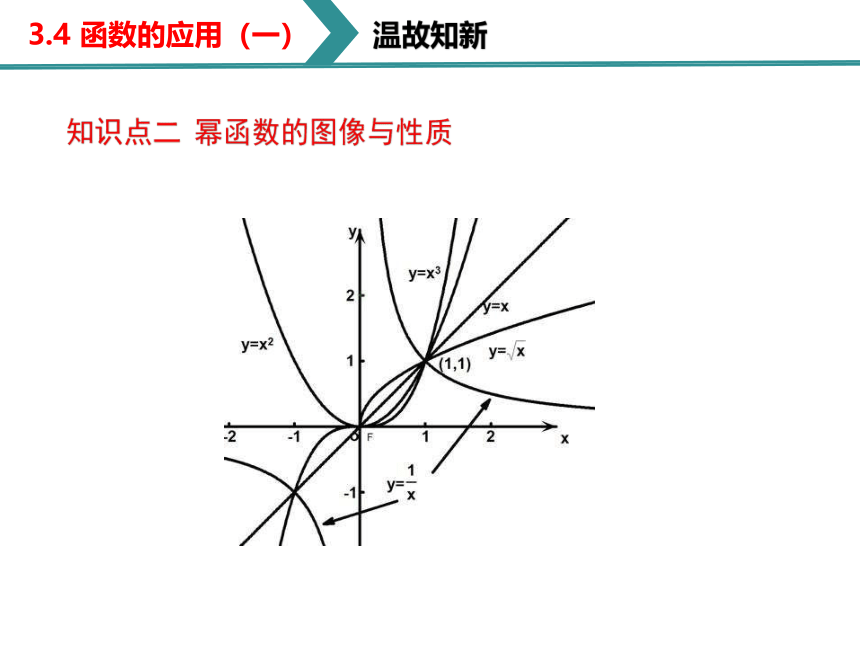
知识点二 幂函数的图像与性质
温故知新
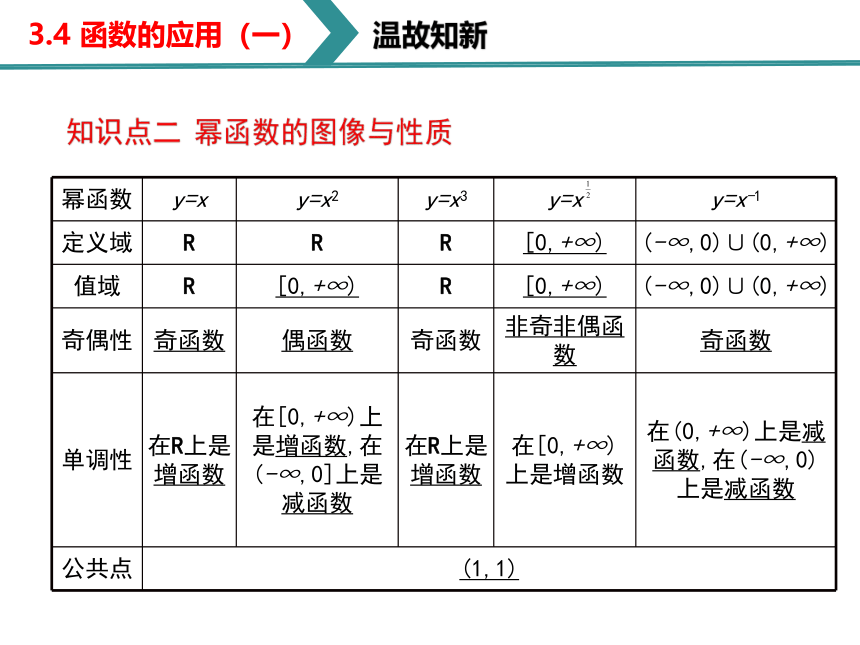
知识点二 幂函数的图像与性质
{5940675A-B579-460E-94D1-54222C63F5DA}幂函数
y=x
y=x2
y=x3
y=x
y=x-1
定义域
R
R
R
[0,+∞)
(-∞,0)∪(0,+∞)
值域
R
[0,+∞)
R
[0,+∞)
(-∞,0)∪(0,+∞)
奇偶性
奇函数
偶函数
奇函数
非奇非偶函数
奇函数
单调性
在R上是增函数
在[0,+∞)上是增函数,在(-∞,0]上是减函数
在R上是增函数
在[0,+∞)上是增函数
在(0,+∞)上是减函数,在(-∞,0)上是减函数
公共点
(1,1)
温故知新
我们学习过了一次函数、二次函数、分段函数、幂函数等都与现实世界有紧密联系,请学生们举例说明与此有关的生活实例.
情景导入
阅读课本93-94页,思考并完成以下问题
1.一、二次函数、反比例函数的表达形式分别是什么?
2.幂函数、分段函数模型的表达形式是什么?
3.解决实际问题的基本过程是?
情景导入
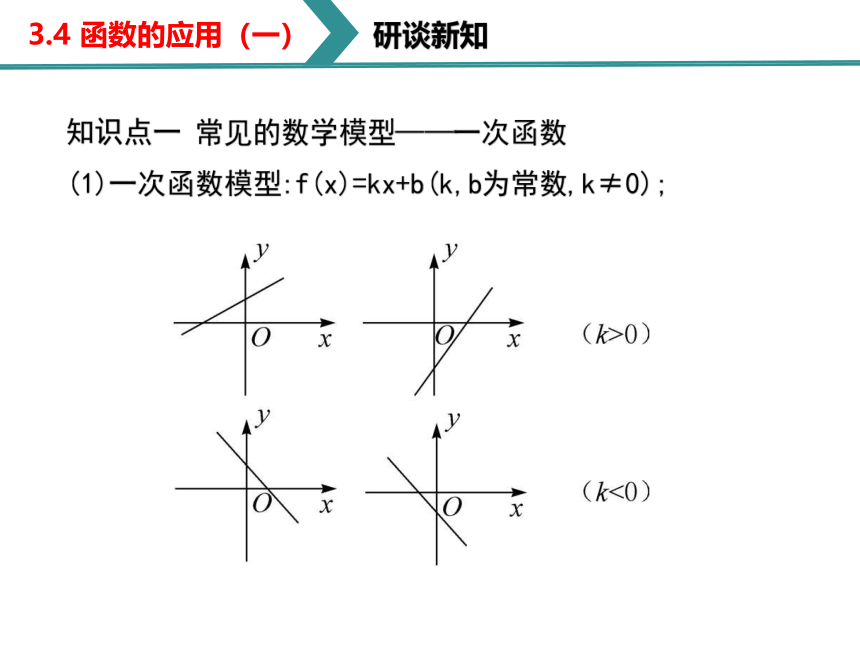
知识点一 常见的数学模型——一次函数
(1)一次函数模型:f(x)=kx+b(k,b为常数,k≠0);
研谈新知
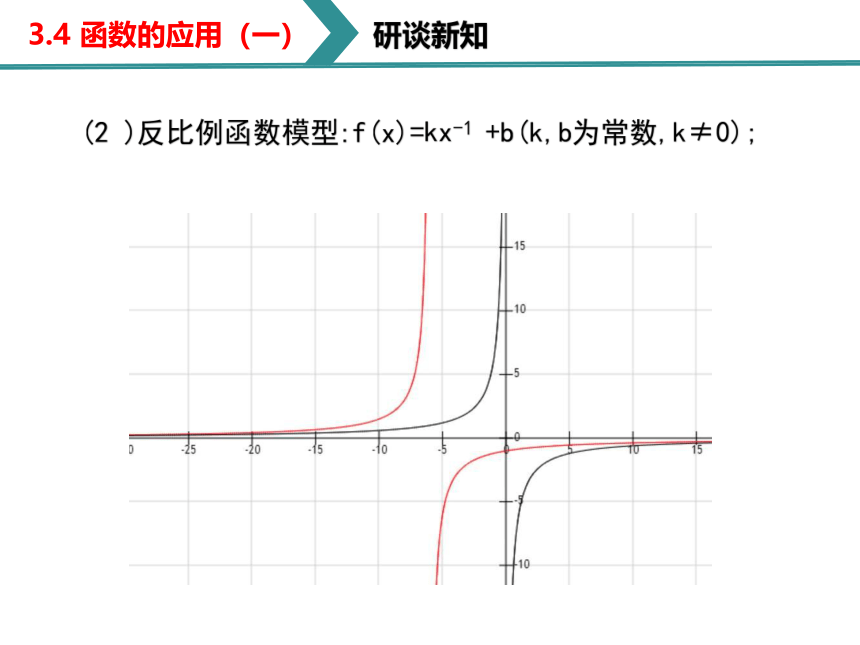
(2 )反比例函数模型:f(x)=kx-1 +b(k,b为常数,k≠0);
研谈新知
(3)二次函数模型:f(x)=ax2+bx+c(a,b,c为常数,a≠0);
研谈新知
(4)幂函数模型:f(x)=axn+b(a,b,n为常数,a≠0,n≠1);
研谈新知
(5)分段函数模型:这个模型实则是以上两种或多种模型的综合,因此应用也十分广泛.
研谈新知
1、某厂日生产文具盒的总成本y(元)与日产量x(套)之间的关系为y=6x+30 000,而出厂价格为每套12元,要使该厂不亏本,至少日生产文具盒( )
A.2 000套 B.3 000套 C.4 000套 D.5 000套
随堂练习
D
解:因利润z=12x-(6x+30 000), 所以z=6x-30 000,
由z≥0解得x≥5 000,故至少日生产文具盒5000套.
3、商店出售茶壶和茶杯,茶壶定价为每个20元,茶杯每个5元,该商店推出两种优惠办法:
①买一个茶壶赠一个茶杯;
②按总价的92%付款.
某顾客需购买茶壶4个,茶杯若干个(不少于4个),若购买茶杯x(个),付款y(元),试分别建立两种优惠办法中y与x之间的函数解析式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更优惠?
随堂练习
解:由优惠办法①可得函数解析式为y1=20×4+5(x-4)=5x+60(x≥4,且x∈N).
由优惠办法②可得y2=(5x+20×4)×92%=4.6x+73.6(x≥4,且x∈N).
y1-y2=0.4x-13.6(x≥4,且x∈N),
令y1-y2=0,得x=34.
所以,当购买34个茶杯时,两种优惠办法付款相同;
当4≤x<34时,y1当x>34时,y1>y2,优惠办法②更省钱.
随堂练习
2、一辆汽车在某段路程中的行驶速度与时间的关系如图所示.
(1)求图中阴影部分的面积,关说明所求面积的实际含义;
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004km,试建立汽车行驶这段路程时汽车里程表读数s与时间t的函数解析式,并作出相应的图象.
随堂练习
2、一辆汽车在某段路程中的行驶速度与时间的关系如图所示.
(1)求图中阴影部分的面积,关说明所求面积的实际含义;
随堂练习
解:阴影部分的面积为
50×1+80×1+90×1+75×1+65×1=360
阴影部分的面积表示汽车在这5 h内行驶的路程为360 km.
2、一辆汽车在某段路程中的行驶速度与时间的关系如图所示.
(2)假设这辆汽车的里程表在汽车行驶这段路程前的
读数为2004km,试建立汽车行驶这段路程时汽车里程
表读数s与时间t的函数解析式,并作出相应的图象.
随堂练习
解:获得路程关于时间变化的函数解析式
2、一辆汽车在某段路程中的行驶速度与时间的关系如图所示.
(2)假设这辆汽车的里程表在汽车行驶这段路程前的
读数为2004km,试建立汽车行驶这段路程时汽车里程
表读数s与时间t的函数解析式,并作出相应的图象.
随堂练习
解:获得路程关于时间变化的函数解析式
1、函数模型
2、分段函数
3、利用函数模型解决实际问题
课堂小结
3.4 函数的应用(一)
重点难点
重点:
运用一次函数、二次函数、幂函数、分段函数模型的处理实际问题;
难点:
运用函数思想理解和处理现实生活和社会中的简单问题.
温故知新
重点:
运用一次函数、二次函数、幂函数、分段函数模型的处理实际问题;
难点:
运用函数思想理解和处理现实生活和社会中的简单问题.
知识点一 幂函数的定义
一般地,函数y=xα叫做幂函数,其中x是自变量,α是常数.
温故知新
知识点二 幂函数的图像与性质
温故知新
知识点二 幂函数的图像与性质
{5940675A-B579-460E-94D1-54222C63F5DA}幂函数
y=x
y=x2
y=x3
y=x
y=x-1
定义域
R
R
R
[0,+∞)
(-∞,0)∪(0,+∞)
值域
R
[0,+∞)
R
[0,+∞)
(-∞,0)∪(0,+∞)
奇偶性
奇函数
偶函数
奇函数
非奇非偶函数
奇函数
单调性
在R上是增函数
在[0,+∞)上是增函数,在(-∞,0]上是减函数
在R上是增函数
在[0,+∞)上是增函数
在(0,+∞)上是减函数,在(-∞,0)上是减函数
公共点
(1,1)
温故知新
我们学习过了一次函数、二次函数、分段函数、幂函数等都与现实世界有紧密联系,请学生们举例说明与此有关的生活实例.
情景导入
阅读课本93-94页,思考并完成以下问题
1.一、二次函数、反比例函数的表达形式分别是什么?
2.幂函数、分段函数模型的表达形式是什么?
3.解决实际问题的基本过程是?
情景导入
知识点一 常见的数学模型——一次函数
(1)一次函数模型:f(x)=kx+b(k,b为常数,k≠0);
研谈新知
(2 )反比例函数模型:f(x)=kx-1 +b(k,b为常数,k≠0);
研谈新知
(3)二次函数模型:f(x)=ax2+bx+c(a,b,c为常数,a≠0);
研谈新知
(4)幂函数模型:f(x)=axn+b(a,b,n为常数,a≠0,n≠1);
研谈新知
(5)分段函数模型:这个模型实则是以上两种或多种模型的综合,因此应用也十分广泛.
研谈新知
1、某厂日生产文具盒的总成本y(元)与日产量x(套)之间的关系为y=6x+30 000,而出厂价格为每套12元,要使该厂不亏本,至少日生产文具盒( )
A.2 000套 B.3 000套 C.4 000套 D.5 000套
随堂练习
D
解:因利润z=12x-(6x+30 000), 所以z=6x-30 000,
由z≥0解得x≥5 000,故至少日生产文具盒5000套.
3、商店出售茶壶和茶杯,茶壶定价为每个20元,茶杯每个5元,该商店推出两种优惠办法:
①买一个茶壶赠一个茶杯;
②按总价的92%付款.
某顾客需购买茶壶4个,茶杯若干个(不少于4个),若购买茶杯x(个),付款y(元),试分别建立两种优惠办法中y与x之间的函数解析式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更优惠?
随堂练习
解:由优惠办法①可得函数解析式为y1=20×4+5(x-4)=5x+60(x≥4,且x∈N).
由优惠办法②可得y2=(5x+20×4)×92%=4.6x+73.6(x≥4,且x∈N).
y1-y2=0.4x-13.6(x≥4,且x∈N),
令y1-y2=0,得x=34.
所以,当购买34个茶杯时,两种优惠办法付款相同;
当4≤x<34时,y1
随堂练习
2、一辆汽车在某段路程中的行驶速度与时间的关系如图所示.
(1)求图中阴影部分的面积,关说明所求面积的实际含义;
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004km,试建立汽车行驶这段路程时汽车里程表读数s与时间t的函数解析式,并作出相应的图象.
随堂练习
2、一辆汽车在某段路程中的行驶速度与时间的关系如图所示.
(1)求图中阴影部分的面积,关说明所求面积的实际含义;
随堂练习
解:阴影部分的面积为
50×1+80×1+90×1+75×1+65×1=360
阴影部分的面积表示汽车在这5 h内行驶的路程为360 km.
2、一辆汽车在某段路程中的行驶速度与时间的关系如图所示.
(2)假设这辆汽车的里程表在汽车行驶这段路程前的
读数为2004km,试建立汽车行驶这段路程时汽车里程
表读数s与时间t的函数解析式,并作出相应的图象.
随堂练习
解:获得路程关于时间变化的函数解析式
2、一辆汽车在某段路程中的行驶速度与时间的关系如图所示.
(2)假设这辆汽车的里程表在汽车行驶这段路程前的
读数为2004km,试建立汽车行驶这段路程时汽车里程
表读数s与时间t的函数解析式,并作出相应的图象.
随堂练习
解:获得路程关于时间变化的函数解析式
1、函数模型
2、分段函数
3、利用函数模型解决实际问题
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
