4.2.2 指数函数的图像和性质 课件(共21张PPT)
文档属性
| 名称 | 4.2.2 指数函数的图像和性质 课件(共21张PPT) |

|
|
| 格式 | rar | ||
| 文件大小 | 200.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-02 00:00:00 | ||
图片预览








文档简介
4.2.2 指数函数的图像和性质
第四章 指数函数与对数函数
教学目标
1、掌握指数函数的图象和性质,培养学生实际应用函数的能力;
2、通过观察图象,分析、归纳、总结指数函数的性质;
3、在指数函数的学习过程中,体验数学的科学价值并养成勇于探索的良好习惯.
重点难点
重点:
指数函数的图象和性质
难点:
对底数的分类,如何由图象、解析式归纳指数函数的性质
温故知新
知识点一 指数函数的定义
函数y=ax(a>0且a≠0)叫做指数函数,其中x是自变量,函数的定义域为R.
知识点二 指数函数解析式的特征
(1)底数a为大于0且不等于1的常数.
(2)自变量x的位置在指数上,且x的系数是1.
(3)ax的系数是1.
温故知新
知识点二 指数函数解析式的特征
(1)底数a为大于0且不等于1的常数.
(2)自变量x的位置在指数上,且x的系数是1.
(3)ax的系数是1.
温故知新
情景导入
请用三点画图法画图像
观察两个函数图像猜测指数函数有哪些性质?
阅读课本116-117页,思考并完成以下问题
1. 结合指数函数的图象,可归纳出指数函数具有哪些性质?
2. 指数函数的图象过哪个定点?如何求指数型函数的定义域和值域问题?
情景导入
研探新知
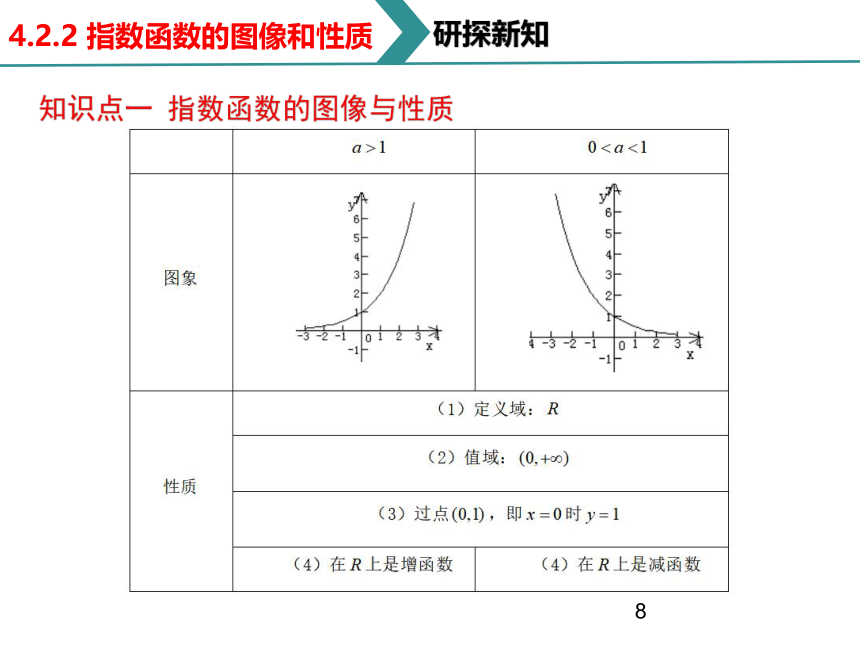
知识点一 指数函数的图像与性质
典型例题
例1 函数y=ax-3+3(a>0,且a≠1)的图象过定点______.
(3,4)
解:因为指数函数y=ax(a>0,且a≠1)的图象过定点(0,1),所以在函数y=ax-3+3中
令x-3=0,得x=3
此时y=1+3=4,
即函数y=ax-3+3的图象过定点(3,4).
典型例题
例2 函数f(x)=ax-b的图象如图所示,其中a,b为常数,则下列结论正确的是( )
A.a>1,b<0
B.a>1,b>0
C.0<a<1,b>0
D. 0<a<1,b<0
D
解:从曲线的变化趋势,可以得到函数f(x)为减函数,
从而有0<a<1;
从曲线位置看,是由函数y=ax(0<a<1)的图象向左平移|-b|个单位长度得到,
所以-b>0,即b<0.
典型例题
例3 画出下列函数的图象,并说明它们是由函数f(x)=2x的图象经过怎样的变换得到的.
(1)y=2x+1 (2)y=-2x
解:(1)y=2x+1的图象是由y=2x的图象向上平移1个单位
长度得到的;
(2)y=-2x的图象与y=2x的图象关于x轴对称.
典型例题
例4 比较下列各题中两个值的大小:
解:(1)由于1.72.5和1.73底数是1.7,故构造函数y=1.7x,
而函数y=1.7x在R上是增函数.
又2.5<3,
∴1.72.5<1.73
典型例题
例4 比较下列各题中两个值的大小:
典型例题
例4 比较下列各题中两个值的大小:
解:(3)由指数函数的性质,
知0.93.1<0.90=1,
1.70.3>1.70=1,
则1.70.3 > 0.93.1
随堂练习
1、 比较下面两个数的大小:
(a-1)1.3与(a-1)2.4(a>1,且a≠2).
解:因为a>1,且a≠2,所以a-1>0,且a-1≠1,
若a-1>1,即a>2,则y=(a-1)x是增函数,
∴(a-1)1.3<(a-1)2.4.
若0∴(a-1)1.3>(a-1)2.4.
故当a>2时,(a-1)1.3<(a-1)2.4;
当1(a-1)2.4.
随堂练习
2、已知函数f(x)=ax+1+3的图象一定过点P,
则点P的坐标是 .
解:∵当x+1=0,即x=-1时,f(x)=a0+3=4恒成立,
故函数f(x)=ax+1+3恒过(-1,4)点.
(-1,4)
随堂练习
3、如图是指数函数:①y=ax,②y=bx,③y=cx,④y=dx的图象,则a,b,c,d与1的大小关系是( )
A.aC.1解:解析:(方法一)①②中函数的底数小于1且大于0,在y轴右边,底数越小,图象向下越靠近x轴,故有b③④中函数的底数大于1,在y轴右边,底数越大,
图象向上越靠近y轴,故有d(方法二)作直线x=1,与函数①,②,③,④的图象分别交于A,B,C,D四点,将x=1代入各个函数可得函数值等于底数值,
所以交点的纵坐标越大,则对应函数的底数越大.
由图可知bB
随堂练习
4、函数y=ax,y=x+a在同一坐标系中的图象可能是( )
解:函数y=x+a单调递增.由题意知a>0且a≠1.
当0当a>1时,y=ax单调递增,直线y=x+a在y轴上的截距大于1.故选D.
D
随堂练习
5、求不等式a4x+5>a2x-1(a>0,且a≠1)中x的取值范围.
解:对于a4x+5>a2x-1(a>0,且a≠1),
当a>1时,有a4x+5>a2x-1,解得x>-3;
当0综上所述:
当a>1时,x的取值范围为{x|x>-3};
当0课堂小结
1、指数函数的图象
2、指数函数的性质
3、利用指数函数进行大小比较
第四章 指数函数与对数函数
教学目标
1、掌握指数函数的图象和性质,培养学生实际应用函数的能力;
2、通过观察图象,分析、归纳、总结指数函数的性质;
3、在指数函数的学习过程中,体验数学的科学价值并养成勇于探索的良好习惯.
重点难点
重点:
指数函数的图象和性质
难点:
对底数的分类,如何由图象、解析式归纳指数函数的性质
温故知新
知识点一 指数函数的定义
函数y=ax(a>0且a≠0)叫做指数函数,其中x是自变量,函数的定义域为R.
知识点二 指数函数解析式的特征
(1)底数a为大于0且不等于1的常数.
(2)自变量x的位置在指数上,且x的系数是1.
(3)ax的系数是1.
温故知新
知识点二 指数函数解析式的特征
(1)底数a为大于0且不等于1的常数.
(2)自变量x的位置在指数上,且x的系数是1.
(3)ax的系数是1.
温故知新
情景导入
请用三点画图法画图像
观察两个函数图像猜测指数函数有哪些性质?
阅读课本116-117页,思考并完成以下问题
1. 结合指数函数的图象,可归纳出指数函数具有哪些性质?
2. 指数函数的图象过哪个定点?如何求指数型函数的定义域和值域问题?
情景导入
研探新知
知识点一 指数函数的图像与性质
典型例题
例1 函数y=ax-3+3(a>0,且a≠1)的图象过定点______.
(3,4)
解:因为指数函数y=ax(a>0,且a≠1)的图象过定点(0,1),所以在函数y=ax-3+3中
令x-3=0,得x=3
此时y=1+3=4,
即函数y=ax-3+3的图象过定点(3,4).
典型例题
例2 函数f(x)=ax-b的图象如图所示,其中a,b为常数,则下列结论正确的是( )
A.a>1,b<0
B.a>1,b>0
C.0<a<1,b>0
D. 0<a<1,b<0
D
解:从曲线的变化趋势,可以得到函数f(x)为减函数,
从而有0<a<1;
从曲线位置看,是由函数y=ax(0<a<1)的图象向左平移|-b|个单位长度得到,
所以-b>0,即b<0.
典型例题
例3 画出下列函数的图象,并说明它们是由函数f(x)=2x的图象经过怎样的变换得到的.
(1)y=2x+1 (2)y=-2x
解:(1)y=2x+1的图象是由y=2x的图象向上平移1个单位
长度得到的;
(2)y=-2x的图象与y=2x的图象关于x轴对称.
典型例题
例4 比较下列各题中两个值的大小:
解:(1)由于1.72.5和1.73底数是1.7,故构造函数y=1.7x,
而函数y=1.7x在R上是增函数.
又2.5<3,
∴1.72.5<1.73
典型例题
例4 比较下列各题中两个值的大小:
典型例题
例4 比较下列各题中两个值的大小:
解:(3)由指数函数的性质,
知0.93.1<0.90=1,
1.70.3>1.70=1,
则1.70.3 > 0.93.1
随堂练习
1、 比较下面两个数的大小:
(a-1)1.3与(a-1)2.4(a>1,且a≠2).
解:因为a>1,且a≠2,所以a-1>0,且a-1≠1,
若a-1>1,即a>2,则y=(a-1)x是增函数,
∴(a-1)1.3<(a-1)2.4.
若0
故当a>2时,(a-1)1.3<(a-1)2.4;
当1
随堂练习
2、已知函数f(x)=ax+1+3的图象一定过点P,
则点P的坐标是 .
解:∵当x+1=0,即x=-1时,f(x)=a0+3=4恒成立,
故函数f(x)=ax+1+3恒过(-1,4)点.
(-1,4)
随堂练习
3、如图是指数函数:①y=ax,②y=bx,③y=cx,④y=dx的图象,则a,b,c,d与1的大小关系是( )
A.a
图象向上越靠近y轴,故有d
所以交点的纵坐标越大,则对应函数的底数越大.
由图可知b
随堂练习
4、函数y=ax,y=x+a在同一坐标系中的图象可能是( )
解:函数y=x+a单调递增.由题意知a>0且a≠1.
当0
D
随堂练习
5、求不等式a4x+5>a2x-1(a>0,且a≠1)中x的取值范围.
解:对于a4x+5>a2x-1(a>0,且a≠1),
当a>1时,有a4x+5>a2x-1,解得x>-3;
当0
当a>1时,x的取值范围为{x|x>-3};
当0
1、指数函数的图象
2、指数函数的性质
3、利用指数函数进行大小比较
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
