4.4.3 不同函数增长的差异 课件(共21张PPT)
文档属性
| 名称 | 4.4.3 不同函数增长的差异 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 175.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-02 17:45:46 | ||
图片预览








文档简介
4.4.3 不同函数增长的差异
第四章 指数函数与对数函数
教学目标
1.掌握常见增长函数的定义、图象、性质,并体会其增长的快慢.
2.理解直线上升、对数增长、指数爆炸的含义以及三种函数模型的性质的比较,培养数学建模和数学运算等核心素养.
重点难点
重点:
比较函数值得大小
难点:
几种增长函数模型的应用
温故知新
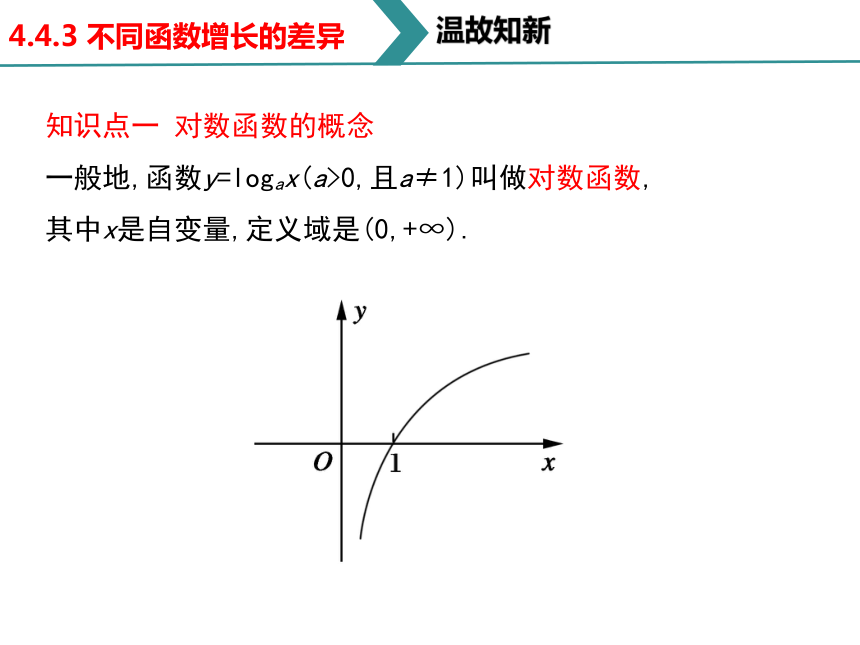
知识点一 对数函数的概念
一般地,函数y=logax(a>0,且a≠1)叫做对数函数,
其中x是自变量,定义域是(0,+∞).
温故知新
知识点二 对数函数的图象与性质
定义
y=logax (a>0,且a≠1)
底数
a>1
0图象
?
?
定义域
(0,+∞)
温故知新
续表
值域
R
单调性
在(0,+∞)上是增函数
在(0,+∞)上是减函数
共点性
图象过定点(1,0)????,即x=1时,y=0
函数值
特点
x∈(0,1)时,y∈(-∞,0);
x∈[1,+∞)时,y∈[0,+∞)
x∈(0,1)时,y∈(0,+∞);
x∈[1,+∞)时,y∈(-∞,0]
对称性
函数y=logax与y=?x的图象关于??x轴????对称
温故知新
知识点三 反函数
一般地,指数函数y=ax(a>0,且a≠1)与对数函数??y=logax(a>0,a≠1)??互为反函数.
它们的定义域与值域正好互换.
互为反函数的两个函数的单调性相同,但单调区间不一定相同.
互为反函数的两个函数的图象关于直线y=x对称.
情景导入
请学生用画图像y=2x和y=2x观察两个函数图像,探索它们在区间[0,+∞)上的增长差异,你能描述一下指数函数增长的特点吗?
情景导入
阅读课本136-138页,思考并完成以下问题
1.三种函数模型的性质?
2.三种函数的增长速度比较?
研探新知
知识点一 常见函数模型的比较
性质函数
y=ax
(a>1)
y=logax
(a>1)
y=kx
(k>0)
在(0,+∞)
上的增减性
增
增
增
图象的变化
随x的增大逐渐变“陡”
随x的增大逐渐趋于稳定
增长速度固定
增长特点
随着自变量的增大,函数值增大的速度越来越快,即增长速度急剧
随着自变量的增大,函数值增大的速度越来越慢,即增长速度平缓
直线上升,其增长速度
不变
增长速度
y=ax(a>1)的增长速度远远快于y=kx(k>0)的增长速度,y=kx(k>0)的增长速度
快于y=logax(a>1)的增长速度
结果
存在一个x0,当x>x0时,有ax>kx,logax研探新知
知识点二 常见的函数模型及增长特点
1.线性函数模型y=kx+b(k>0)的增长特点是直线上升,其增长速度不变.
研探新知
知识点二 常见的函数模型及增长特点
2.指数函数模型y=ax(a>1)的增长特点是随着自变量的增大,函数值增大的速度越来越快,即增长速度急剧,形象地称为“指数爆炸”.
研探新知
知识点二 常见的函数模型及增长特点
3.对数函数模型y=logax(a>1)的增长特点是随着自变量的增大,函数值增大的速度越来越慢,即增长速度平缓.
随堂练习
1.有一组实验数据如下表所示:下列所给函数模型较适合的是( )
A.y=logax(a>1) B.y=ax+b(a>1)
C.y=ax2+b(a>0) D.y=logax+b(a>1)
{5940675A-B579-460E-94D1-54222C63F5DA}x
1
2
3
4
5
y
1.5
5.9
13.4
24.1
37
C
解:通过所给数据可知y随x增大,其增长速度越来越快,而A,D中的函数增长速度越来越慢,而B中的函数增长速度保持不变,故选C.
随堂练习
2.若 ,则下列结论正确的是( )
A
解:如图所示,易知选择A
随堂练习
3.某林区的森林蓄积量每年比上一年平均增长10.4%,要增长到原来的y倍,需经过x年,则函数y=f(x)的图象大致为( )
A. B. C. D.
B
解:根据题意,.
函数解析式为 y=1.104x(x>0)函数为指数函数,
底数1.104>1递增,选B
随堂练习
4.四人赛跑,假设他们跑过的路程fi(x)(其中i∈{1,2,3,4})和时间x(x>1)的函数关系分别是f1(x)=x2,f2(x)=4x,f3(x)=log2x,f4(x)=2x,如果他们一直跑下去,最终跑在最前面的人具有的函数关系是( )
A.f1(x)=x2 B.f2(x)=4x C.f3(x)=log2x f4(x)=2x
D
解:由函数的增长趋势可知,指数函数增长最快,所以最终最前面的具有的函数关系为f4(x)=2x,故选D
随堂练习
5.每年的3月12日是植树节,全国各地在这一天都会开展各种形式的植树活动,某市现有树木面积10万平方米,计划今后5年内扩大树木面积,现有两种方案如下:
方案一:每年植树1万平方米;
方案二:每年树木面积比上一年增加9%.
哪个方案较好?
分析:最优方案问题,需要将两种方案的函数模型都求解出来,再进行比较,得到最优方案。
随堂练习
5.每年的3月12日是植树节,全国各地在这一天都会开展各种形式的植树活动,某市现有树木面积10万平方米,计划今后5年内扩大树木面积,现有两种方案如下:
方案一:每年植树1万平方米;
方案二:每年树木面积比上一年增加9%.
哪个方案较好?
解:方案一:的函数模型为y=x+10,
5年后树木面积为:10+1×5=15(万平方米)
方案二的函数模型为y=(1+9%)x
5年后树木面积为:10(1+9%)5≈15.386(万平方米).
因为15.386>15,
所以方案二较好.
随堂练习
1、三中常见函数模型的比较
2、常见的函数模型及增长特点
第四章 指数函数与对数函数
教学目标
1.掌握常见增长函数的定义、图象、性质,并体会其增长的快慢.
2.理解直线上升、对数增长、指数爆炸的含义以及三种函数模型的性质的比较,培养数学建模和数学运算等核心素养.
重点难点
重点:
比较函数值得大小
难点:
几种增长函数模型的应用
温故知新
知识点一 对数函数的概念
一般地,函数y=logax(a>0,且a≠1)叫做对数函数,
其中x是自变量,定义域是(0,+∞).
温故知新
知识点二 对数函数的图象与性质
定义
y=logax (a>0,且a≠1)
底数
a>1
0
?
?
定义域
(0,+∞)
温故知新
续表
值域
R
单调性
在(0,+∞)上是增函数
在(0,+∞)上是减函数
共点性
图象过定点(1,0)????,即x=1时,y=0
函数值
特点
x∈(0,1)时,y∈(-∞,0);
x∈[1,+∞)时,y∈[0,+∞)
x∈(0,1)时,y∈(0,+∞);
x∈[1,+∞)时,y∈(-∞,0]
对称性
函数y=logax与y=?x的图象关于??x轴????对称
温故知新
知识点三 反函数
一般地,指数函数y=ax(a>0,且a≠1)与对数函数??y=logax(a>0,a≠1)??互为反函数.
它们的定义域与值域正好互换.
互为反函数的两个函数的单调性相同,但单调区间不一定相同.
互为反函数的两个函数的图象关于直线y=x对称.
情景导入
请学生用画图像y=2x和y=2x观察两个函数图像,探索它们在区间[0,+∞)上的增长差异,你能描述一下指数函数增长的特点吗?
情景导入
阅读课本136-138页,思考并完成以下问题
1.三种函数模型的性质?
2.三种函数的增长速度比较?
研探新知
知识点一 常见函数模型的比较
性质函数
y=ax
(a>1)
y=logax
(a>1)
y=kx
(k>0)
在(0,+∞)
上的增减性
增
增
增
图象的变化
随x的增大逐渐变“陡”
随x的增大逐渐趋于稳定
增长速度固定
增长特点
随着自变量的增大,函数值增大的速度越来越快,即增长速度急剧
随着自变量的增大,函数值增大的速度越来越慢,即增长速度平缓
直线上升,其增长速度
不变
增长速度
y=ax(a>1)的增长速度远远快于y=kx(k>0)的增长速度,y=kx(k>0)的增长速度
快于y=logax(a>1)的增长速度
结果
存在一个x0,当x>x0时,有ax>kx,logax
知识点二 常见的函数模型及增长特点
1.线性函数模型y=kx+b(k>0)的增长特点是直线上升,其增长速度不变.
研探新知
知识点二 常见的函数模型及增长特点
2.指数函数模型y=ax(a>1)的增长特点是随着自变量的增大,函数值增大的速度越来越快,即增长速度急剧,形象地称为“指数爆炸”.
研探新知
知识点二 常见的函数模型及增长特点
3.对数函数模型y=logax(a>1)的增长特点是随着自变量的增大,函数值增大的速度越来越慢,即增长速度平缓.
随堂练习
1.有一组实验数据如下表所示:下列所给函数模型较适合的是( )
A.y=logax(a>1) B.y=ax+b(a>1)
C.y=ax2+b(a>0) D.y=logax+b(a>1)
{5940675A-B579-460E-94D1-54222C63F5DA}x
1
2
3
4
5
y
1.5
5.9
13.4
24.1
37
C
解:通过所给数据可知y随x增大,其增长速度越来越快,而A,D中的函数增长速度越来越慢,而B中的函数增长速度保持不变,故选C.
随堂练习
2.若 ,则下列结论正确的是( )
A
解:如图所示,易知选择A
随堂练习
3.某林区的森林蓄积量每年比上一年平均增长10.4%,要增长到原来的y倍,需经过x年,则函数y=f(x)的图象大致为( )
A. B. C. D.
B
解:根据题意,.
函数解析式为 y=1.104x(x>0)函数为指数函数,
底数1.104>1递增,选B
随堂练习
4.四人赛跑,假设他们跑过的路程fi(x)(其中i∈{1,2,3,4})和时间x(x>1)的函数关系分别是f1(x)=x2,f2(x)=4x,f3(x)=log2x,f4(x)=2x,如果他们一直跑下去,最终跑在最前面的人具有的函数关系是( )
A.f1(x)=x2 B.f2(x)=4x C.f3(x)=log2x f4(x)=2x
D
解:由函数的增长趋势可知,指数函数增长最快,所以最终最前面的具有的函数关系为f4(x)=2x,故选D
随堂练习
5.每年的3月12日是植树节,全国各地在这一天都会开展各种形式的植树活动,某市现有树木面积10万平方米,计划今后5年内扩大树木面积,现有两种方案如下:
方案一:每年植树1万平方米;
方案二:每年树木面积比上一年增加9%.
哪个方案较好?
分析:最优方案问题,需要将两种方案的函数模型都求解出来,再进行比较,得到最优方案。
随堂练习
5.每年的3月12日是植树节,全国各地在这一天都会开展各种形式的植树活动,某市现有树木面积10万平方米,计划今后5年内扩大树木面积,现有两种方案如下:
方案一:每年植树1万平方米;
方案二:每年树木面积比上一年增加9%.
哪个方案较好?
解:方案一:的函数模型为y=x+10,
5年后树木面积为:10+1×5=15(万平方米)
方案二的函数模型为y=(1+9%)x
5年后树木面积为:10(1+9%)5≈15.386(万平方米).
因为15.386>15,
所以方案二较好.
随堂练习
1、三中常见函数模型的比较
2、常见的函数模型及增长特点
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
