4.5.3 函数模型的应用(二) 课件(共22张PPT)
文档属性
| 名称 | 4.5.3 函数模型的应用(二) 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 430.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-02 17:55:28 | ||
图片预览






文档简介
4.5.3 函数模型的应用(二)
第四章 指数函数与对数函数
教学目标
1.能建立函数模型解决实际问题.
2.了解拟合函数模型并解决实际问题.
3.通过本节内容的学习,使学生认识函数模型的作用,提高学生数学建模,数据分析的能力.
重点难点
重点:
利用给定的函数模型或建立确定性函数模型解决实际问题.
难点:
利用给定的函数模型或建立确定性函数模型解决实际问题,并对给定的函数模型进行简单的分析评价.
温故知新
知识点一 二分法
对于在区间[a,b]上图象连续不断且????f(a)f(b)<0????的函数y=f(x),通过不断地把它的零点所在区间 一分为二????,使所得区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
温故知新
知识点二 用二分法求函数y=f(x)零点近似值的步骤
给定精确度ε,用二分法求函数y=f(x)零点x0的近
似值的一般步骤如下:
1.确定零点x0的初始区间[a,b],验证⑨????f(a)f(b)<0????.
2.求区间(a,b)的中点c.
3.计算f(c),并进一步确定零点所在的区间:
(1)若f(c)=0(此时x0=c),则c就是函数的零点;
(2)若f(a)f(c)<0 (此时x0∈⑩ (a,c)????),则令b=c;
(3)若f(c)f(b)<0(此时x0∈? (c,b)????),则令a=c.
4.判断是否达到精确度ε:若|a-b|<ε,则得到零点近似值a(或b);否则重复步骤2—4.
情景导入
回顾第三章3.4 函数的应用(一),
归纳我们学习过哪些常见的函数模型
知识点一 常见的数学模型
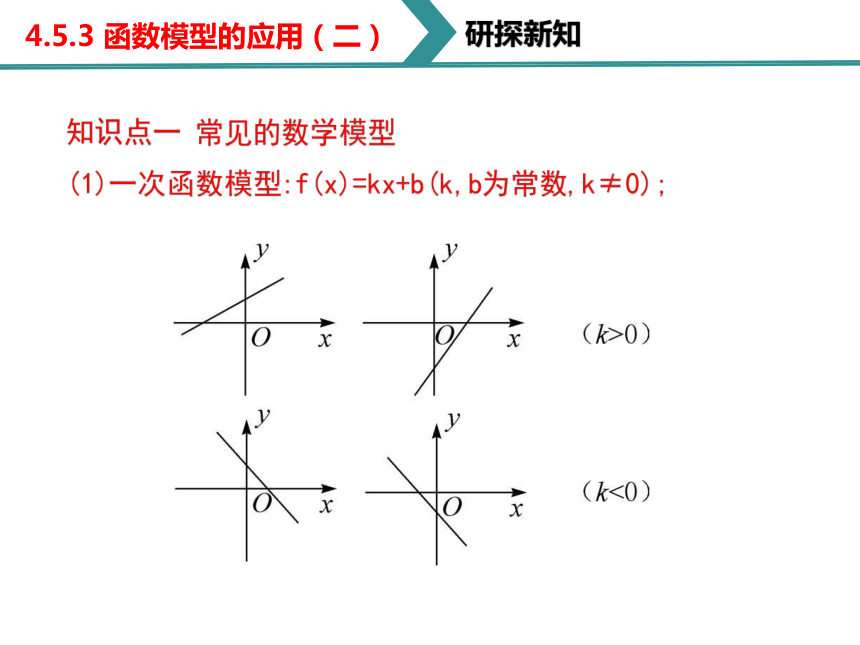
(1)一次函数模型:f(x)=kx+b(k,b为常数,k≠0);
研探新知
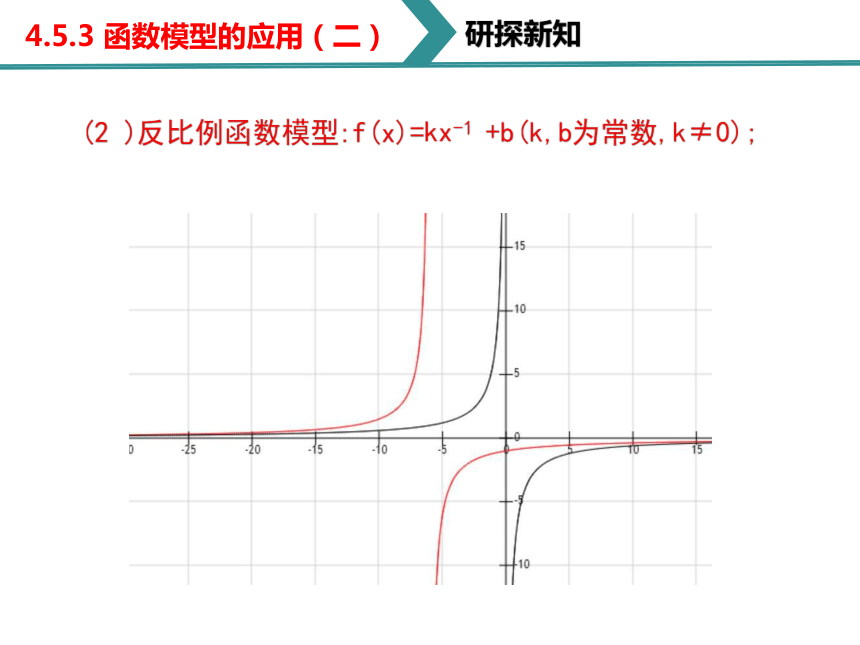
(2 )反比例函数模型:f(x)=kx-1 +b(k,b为常数,k≠0);
研探新知
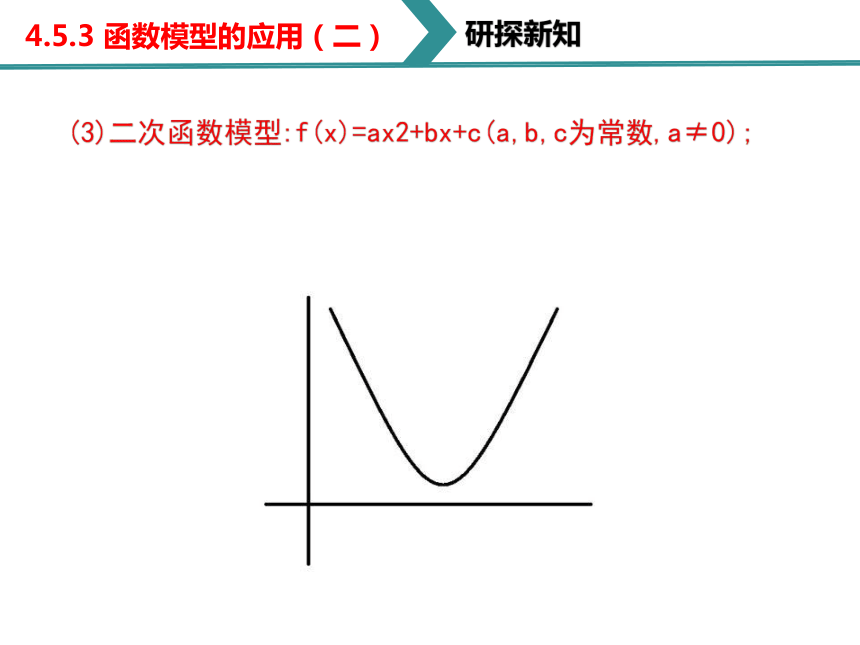
(3)二次函数模型:f(x)=ax2+bx+c(a,b,c为常数,a≠0);
研探新知
(4)幂函数模型:f(x)=axn+b(a,b,n为常数,a≠0,n≠1);
研探新知
(5)分段函数模型:这个模型实则是以上两种或多种模型的综合,因此应用也十分广泛.
研探新知
研探新知
知识点二 用函数模型解决实际问题的基本过程
研探新知
知识点三 建立函数模型解决实际问题的步骤
(1)审题——弄清题意,分清条件和要求的结论,理顺数量关系,初步选择函数模型;
(2)建模——将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知
识建立相应的函数模型;
(3)求模——推理并求解函数模型;
(4)还原——用得到的函数模型描述实际问题的变化规律.
随堂练习
1.根据统计,一名工人组装第x件某产品所用的时间(单位:
分钟)为 已知该工人组装第4件产品用时30分钟,组装第a件产品用时5分钟,那么c和a的值分别是( )
A.75,25 B.75,16 C.60,144 D.60,16
C
随堂练习
2.据统计,每年到鄱阳湖国家湿地公园越冬的白鹤数量y(只)与时间x(年)近似满足关系式:y=alog3(x+2),观测发现2019年冬(作为第1年)有越冬白鹤3 000只,估计到2025年冬越冬白鹤有( )
A.4 000只 B.5 000只 C.6 000只 D.7 000只
解:当x=1时,由3 000=alog3(1+2)得a=3 000,所以到2025年冬,即第7年,y=3 000×log3(7+2)=6 000.故选C.
C
随堂练习
3.某公司在甲、乙两地同时销售一种品牌车,利润(单位:万元)分别为L1=-x2+21x和L2=2x,其中销售量为x(单位:辆).若该公司在两地共销售15辆,则能获得的最大利润为( )
A.90万元 B.120万元 C.120.25万元 D.60万元
B
随堂练习
4.某“红豆生南国,春来发几枝?”下图给出了红豆生长时间t(月)与枝数y的散点图,那么红豆的枝数与生长时间的关系用下列哪个函数模型拟合最好?( )
A.指数函数y=2t B.对数函数y=log2t
C.幂函数y=t3 D.二次函数y=2t2
解:根据已知所给的散点图,观察到图象在第一象限,且从左到右图象是上升的,并且增长速度越来越快,根据四个选项中函数的增长趋势可得,用指数函数模拟较好,
故选A
A
随堂练习
5.(2020山东烟台高一上期末)某商家准备在2020年春节来临前连续两次对某一商品的销售价格进行提价且每次提价10%,然后在春节活动期间连续两次对该商品进行降价且每次降价10%,则该商品的最终售价与原来的价格相比( )
A.略有降低 B.略有提高 C.相等 D.无法确定
解:设这种商品的原价为a,则两次提价后的价格为a(1+10%)2=1.12·a,
又进行两次降价后的价格为
1.12·a(1-10%)2=(1+0.1)2(1-0.1)2·a=0.992a因此最终售价与原来的价格相比略有降低,故选A.
A
随堂练习
6.(2020北京人大附中高一上期中,)如图是吴老师散步时所走的离家距离(y)与行走时间(x)之间的函数关系的图象,若用黑点表示吴老师家的位置,则吴老师散步行走的路线可能是( )
D
解:根据题中图象可知在第一段时间吴老师离家的距离随着时间的增加而增加,第二段时间吴老师离家的距离随着时间的增加不变,第三段时间吴老师离家的距离随着时间的增加而减少,最后回到始点位置,对比各选项可知,只有选项D正确,故选D.
随堂练习
7.现测得(x,y)的两组值为(1,2),(2,5),现有两个拟合模型,甲:y=x2+1,乙:y=3x-1,若又测得(x,y)的一组对应值为(3,10.2),则应选用 作为拟合模型较好.?
解:对于甲:x=3时,y=32+1=10,
对于乙:x=3时,y=8,因此用甲作为拟合模型较好.
甲
课堂小结
1.常见的函数模型
2.用函数模型解决实际问题的基本过程
3.建立函数模型解决实际问题的步骤
第四章 指数函数与对数函数
教学目标
1.能建立函数模型解决实际问题.
2.了解拟合函数模型并解决实际问题.
3.通过本节内容的学习,使学生认识函数模型的作用,提高学生数学建模,数据分析的能力.
重点难点
重点:
利用给定的函数模型或建立确定性函数模型解决实际问题.
难点:
利用给定的函数模型或建立确定性函数模型解决实际问题,并对给定的函数模型进行简单的分析评价.
温故知新
知识点一 二分法
对于在区间[a,b]上图象连续不断且????f(a)f(b)<0????的函数y=f(x),通过不断地把它的零点所在区间 一分为二????,使所得区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
温故知新
知识点二 用二分法求函数y=f(x)零点近似值的步骤
给定精确度ε,用二分法求函数y=f(x)零点x0的近
似值的一般步骤如下:
1.确定零点x0的初始区间[a,b],验证⑨????f(a)f(b)<0????.
2.求区间(a,b)的中点c.
3.计算f(c),并进一步确定零点所在的区间:
(1)若f(c)=0(此时x0=c),则c就是函数的零点;
(2)若f(a)f(c)<0 (此时x0∈⑩ (a,c)????),则令b=c;
(3)若f(c)f(b)<0(此时x0∈? (c,b)????),则令a=c.
4.判断是否达到精确度ε:若|a-b|<ε,则得到零点近似值a(或b);否则重复步骤2—4.
情景导入
回顾第三章3.4 函数的应用(一),
归纳我们学习过哪些常见的函数模型
知识点一 常见的数学模型
(1)一次函数模型:f(x)=kx+b(k,b为常数,k≠0);
研探新知
(2 )反比例函数模型:f(x)=kx-1 +b(k,b为常数,k≠0);
研探新知
(3)二次函数模型:f(x)=ax2+bx+c(a,b,c为常数,a≠0);
研探新知
(4)幂函数模型:f(x)=axn+b(a,b,n为常数,a≠0,n≠1);
研探新知
(5)分段函数模型:这个模型实则是以上两种或多种模型的综合,因此应用也十分广泛.
研探新知
研探新知
知识点二 用函数模型解决实际问题的基本过程
研探新知
知识点三 建立函数模型解决实际问题的步骤
(1)审题——弄清题意,分清条件和要求的结论,理顺数量关系,初步选择函数模型;
(2)建模——将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知
识建立相应的函数模型;
(3)求模——推理并求解函数模型;
(4)还原——用得到的函数模型描述实际问题的变化规律.
随堂练习
1.根据统计,一名工人组装第x件某产品所用的时间(单位:
分钟)为 已知该工人组装第4件产品用时30分钟,组装第a件产品用时5分钟,那么c和a的值分别是( )
A.75,25 B.75,16 C.60,144 D.60,16
C
随堂练习
2.据统计,每年到鄱阳湖国家湿地公园越冬的白鹤数量y(只)与时间x(年)近似满足关系式:y=alog3(x+2),观测发现2019年冬(作为第1年)有越冬白鹤3 000只,估计到2025年冬越冬白鹤有( )
A.4 000只 B.5 000只 C.6 000只 D.7 000只
解:当x=1时,由3 000=alog3(1+2)得a=3 000,所以到2025年冬,即第7年,y=3 000×log3(7+2)=6 000.故选C.
C
随堂练习
3.某公司在甲、乙两地同时销售一种品牌车,利润(单位:万元)分别为L1=-x2+21x和L2=2x,其中销售量为x(单位:辆).若该公司在两地共销售15辆,则能获得的最大利润为( )
A.90万元 B.120万元 C.120.25万元 D.60万元
B
随堂练习
4.某“红豆生南国,春来发几枝?”下图给出了红豆生长时间t(月)与枝数y的散点图,那么红豆的枝数与生长时间的关系用下列哪个函数模型拟合最好?( )
A.指数函数y=2t B.对数函数y=log2t
C.幂函数y=t3 D.二次函数y=2t2
解:根据已知所给的散点图,观察到图象在第一象限,且从左到右图象是上升的,并且增长速度越来越快,根据四个选项中函数的增长趋势可得,用指数函数模拟较好,
故选A
A
随堂练习
5.(2020山东烟台高一上期末)某商家准备在2020年春节来临前连续两次对某一商品的销售价格进行提价且每次提价10%,然后在春节活动期间连续两次对该商品进行降价且每次降价10%,则该商品的最终售价与原来的价格相比( )
A.略有降低 B.略有提高 C.相等 D.无法确定
解:设这种商品的原价为a,则两次提价后的价格为a(1+10%)2=1.12·a,
又进行两次降价后的价格为
1.12·a(1-10%)2=(1+0.1)2(1-0.1)2·a=0.992a
A
随堂练习
6.(2020北京人大附中高一上期中,)如图是吴老师散步时所走的离家距离(y)与行走时间(x)之间的函数关系的图象,若用黑点表示吴老师家的位置,则吴老师散步行走的路线可能是( )
D
解:根据题中图象可知在第一段时间吴老师离家的距离随着时间的增加而增加,第二段时间吴老师离家的距离随着时间的增加不变,第三段时间吴老师离家的距离随着时间的增加而减少,最后回到始点位置,对比各选项可知,只有选项D正确,故选D.
随堂练习
7.现测得(x,y)的两组值为(1,2),(2,5),现有两个拟合模型,甲:y=x2+1,乙:y=3x-1,若又测得(x,y)的一组对应值为(3,10.2),则应选用 作为拟合模型较好.?
解:对于甲:x=3时,y=32+1=10,
对于乙:x=3时,y=8,因此用甲作为拟合模型较好.
甲
课堂小结
1.常见的函数模型
2.用函数模型解决实际问题的基本过程
3.建立函数模型解决实际问题的步骤
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
