江西省赣州市南康中学2020-2021学年高二上学期第二次大考数学(理)试题 Word版含答案
文档属性
| 名称 | 江西省赣州市南康中学2020-2021学年高二上学期第二次大考数学(理)试题 Word版含答案 |
|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-29 00:00:00 | ||
图片预览




文档简介
南康中学2020-2021学年度第一学期高二第二次大考
数 学(理)试 卷
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,有且只有一项是符合题目要求的 )
1.直线的方程为,则直线的倾斜角为( )
A. B. C. D.
2.在空间直角坐标系中,已知,,则的中点到坐标原点的距离为( )
A. B. C.2 D.3
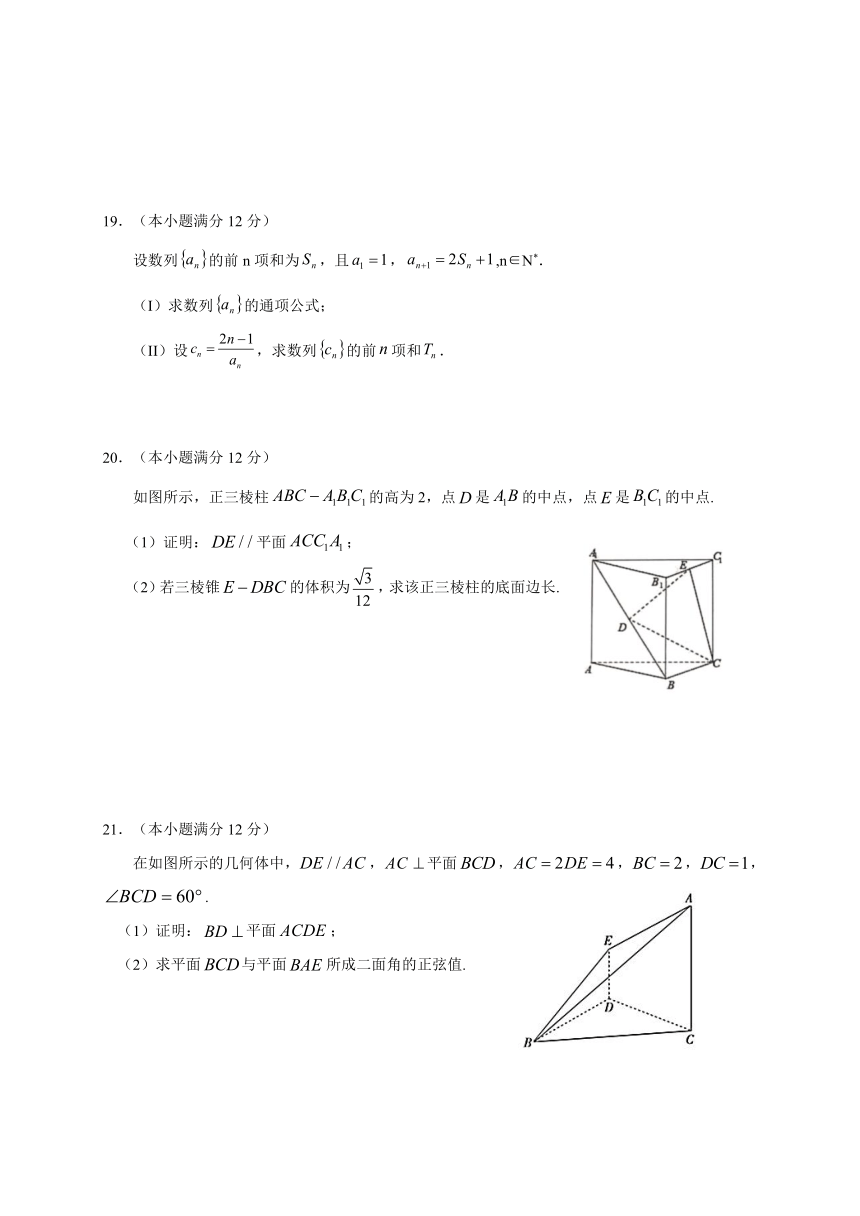
3.一个长方体切去一个小长方体,所得几何体的主视图与左视图分别如图所示,则该几何体的俯视图为( )
4.圆锥的高扩大到原来的倍,底面半径缩短到原来的,则圆锥的体积( )
A.扩大到原来的倍 B.缩小到原来的一半 C.缩小到原来的 D. 不变
5.等比数列,满足,且,,则( )
A.31 B.36 C.42 D.48
6.在棱长为1的正方体中,分别是和的
中点,则直线与所成角的余弦值为( )
A. B.
C. D.
7.圆x2+y2-4x-4y-10=0上的点到直线x+y-14=0的最大距离与最小距离的差是 ( )
A. 36 B. 18 C. 5 D. 6
8.在中,角,,的对边分别为,,,若,则为( )
A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.等腰或直角三角形
9. 已知空间中不同直线和不同平面、,下面四个结论:
①若互为异面直线,,,,,则;
②若,,,则;
③若,,则;
④若,,,则.其中正确的是( )
A. ①② B. ②③ C. ③④ D. ①③
10.唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题——“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为,若将军从点处出发,河岸线所在直线方程为,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
A. B. C. D.
11.已知正方体的棱长为1,是棱的中点,点在正方体内部或正方体的表面上,且∥平面,则动点的轨迹所形成的区域面积是(? )
A. B. C. D.
12.如图,矩形中,,为边的中点,将沿直线翻转成 (平面).若、分别为线段、的中点,则在翻转过程中,下列说法错误的是( )
A.与平面垂直的直线必与直线垂直
B.异面直线与所成角是定值
C.一定存在某个位置,使
D.三棱锥外接球半径与棱的长之比为定值
二、填空题(本大题共4小题,每小题5分,共20分.将答案填在答题卡上的相应位置)
13.已知向量,若向量与垂直,则 .
14.如图,为水平放置的斜二测画法的直观图,且,则的周长为 .
15.在平面直角坐标系中,若圆C:上存在两点A、B满足:,则实数a的最大值是 .
16.已知边长为的菱形中,,沿对角线折成二面角为的四面体,则四面体的外接球的表面积为 .
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤 )
17.(本小题满分10分)
如图,在直三棱柱中,,,,点是的中点.
(1)求证:;
(2)求证:平面.
18.(本小题满分12分)
在中,.
(I)求的大小;
(II)求的最大值.
19.(本小题满分12分)
设数列的前n项和为,且,,n∈N*.
(I)求数列的通项公式;
(II)设,求数列的前项和.
20.(本小题满分12分)
如图所示,正三棱柱的高为2,点是的中点,点是的中点.
(1)证明:平面;
(2)若三棱锥的体积为,求该正三棱柱的底面边长.
21.(本小题满分12分)
在如图所示的几何体中,,平面,,,,.
(1)证明:平面;
(2)求平面与平面所成二面角的正弦值.
22.(本小题满分12分)
如图,在直角坐标系中,圆与轴负半轴交于点,过点的直线,分别与圆交于两点,设直线的斜率分别为.
(1)若,求△的面积;
(2)若,求证:直线过定点.
南康中学2020-2021学年度第一学期高二第二次大考
数学(理)参考答案
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,有且只有一项是符合题目要求的 )
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A A D B A B D D D A C C
二、填空题(本大题共4小题,每小题5分,共20分.将答案填在答题卡上的相应位置)
13. 7 14. 15. 16.
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤 )
17.解: (1)直三棱柱,面,,
又,,,,,
,面,.----------5分
(2)取的中点,连结和,
,且,
四边形为平行四边形,
,面,
,且,四边形为平行四边形,,面,
,面面,平面.----------10分
18.解: (1),又∵,∴......................6分
(2)由(1)知
............................ 10分
因为,所以当时,取得最大值.................................12分
19.解:(1)由an+1=2Sn+1可得an=2Sn﹣1+1(n≥2),两式相减得an+1﹣an=2an
即an+1=3an(n≥2).又a2=2S1+1=3,所以a2=3a1.故{an}是首项为1,公比为3的等比数列.
所以an=3n﹣1. ................................................................5分
(2)因为 ,所以.
则,
两式相减得:.
所以=............................................................12分
20. 解:(1)如图,连接,因为是的中点,是的中点,
所以在中,,
平面, 平面,
所以平面. -------------5分
(2)由等体积法,得,
因为是的中点,
所以点到平面的距离是点到平面的距离的一半.
如图,作交于点,由正三棱柱的性质可知,平面.
设底面正三角形的边长,则三棱锥的高, ------------9分
,
所以,解得,
所以该正三棱柱的底面边长为. -------------12分
21.解:(1)在中,.
所以,所以为直角三角形,. -------------3分
又因为平面,所以.
而,所以平面. -------------5分
(2)(方法一)如图延长,相交于,连接,
则平面平面.
二面角就是平面与平面所成二面角.
因为,所以是的中位线.
,这样是等边三角形.
取的中点为,连接,因为平面.
所以就是二面角的平面角. -------------10分
在,所以. -------------12分
(方法二)建立如图所示的空间直角坐标系,
可得.
.
设是平面的法向量,则
令得. -------------9分
取平面的法向量为. -------------10分
设平面与平面所成二面角的平面角为,
则,从而. -------------12分
22.解:(1)由题知,得直线AM的方程为,直线AN的方程为
所以,圆心到直线AM的距离,所以,,-------------3分
由题知,所以AN⊥AM,,-----------5分
(2)方法一:由题知直线AM的方程,直线AN的方程为
联立方程,所以,
得或 所以,-------------7分
同理,,-------------8分
所以直线为
即,得,
所以直线恒过定点.-------------12分
方法二:由知直线的斜率不为0,
设直线的方程为,
联立 得
且 -------------7分
,
又
即
-------------9分
化简整理得,解得或(舍去) -------------11分
直线的方程为,故直线恒过定点 -------------12分
数 学(理)试 卷
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,有且只有一项是符合题目要求的 )
1.直线的方程为,则直线的倾斜角为( )
A. B. C. D.
2.在空间直角坐标系中,已知,,则的中点到坐标原点的距离为( )
A. B. C.2 D.3
3.一个长方体切去一个小长方体,所得几何体的主视图与左视图分别如图所示,则该几何体的俯视图为( )
4.圆锥的高扩大到原来的倍,底面半径缩短到原来的,则圆锥的体积( )
A.扩大到原来的倍 B.缩小到原来的一半 C.缩小到原来的 D. 不变
5.等比数列,满足,且,,则( )
A.31 B.36 C.42 D.48
6.在棱长为1的正方体中,分别是和的
中点,则直线与所成角的余弦值为( )
A. B.
C. D.
7.圆x2+y2-4x-4y-10=0上的点到直线x+y-14=0的最大距离与最小距离的差是 ( )
A. 36 B. 18 C. 5 D. 6
8.在中,角,,的对边分别为,,,若,则为( )
A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.等腰或直角三角形
9. 已知空间中不同直线和不同平面、,下面四个结论:
①若互为异面直线,,,,,则;
②若,,,则;
③若,,则;
④若,,,则.其中正确的是( )
A. ①② B. ②③ C. ③④ D. ①③
10.唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题——“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为,若将军从点处出发,河岸线所在直线方程为,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
A. B. C. D.
11.已知正方体的棱长为1,是棱的中点,点在正方体内部或正方体的表面上,且∥平面,则动点的轨迹所形成的区域面积是(? )
A. B. C. D.
12.如图,矩形中,,为边的中点,将沿直线翻转成 (平面).若、分别为线段、的中点,则在翻转过程中,下列说法错误的是( )
A.与平面垂直的直线必与直线垂直
B.异面直线与所成角是定值
C.一定存在某个位置,使
D.三棱锥外接球半径与棱的长之比为定值
二、填空题(本大题共4小题,每小题5分,共20分.将答案填在答题卡上的相应位置)
13.已知向量,若向量与垂直,则 .
14.如图,为水平放置的斜二测画法的直观图,且,则的周长为 .
15.在平面直角坐标系中,若圆C:上存在两点A、B满足:,则实数a的最大值是 .
16.已知边长为的菱形中,,沿对角线折成二面角为的四面体,则四面体的外接球的表面积为 .
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤 )
17.(本小题满分10分)
如图,在直三棱柱中,,,,点是的中点.
(1)求证:;
(2)求证:平面.
18.(本小题满分12分)
在中,.
(I)求的大小;
(II)求的最大值.
19.(本小题满分12分)
设数列的前n项和为,且,,n∈N*.
(I)求数列的通项公式;
(II)设,求数列的前项和.
20.(本小题满分12分)
如图所示,正三棱柱的高为2,点是的中点,点是的中点.
(1)证明:平面;
(2)若三棱锥的体积为,求该正三棱柱的底面边长.
21.(本小题满分12分)
在如图所示的几何体中,,平面,,,,.
(1)证明:平面;
(2)求平面与平面所成二面角的正弦值.
22.(本小题满分12分)
如图,在直角坐标系中,圆与轴负半轴交于点,过点的直线,分别与圆交于两点,设直线的斜率分别为.
(1)若,求△的面积;
(2)若,求证:直线过定点.
南康中学2020-2021学年度第一学期高二第二次大考
数学(理)参考答案
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,有且只有一项是符合题目要求的 )
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A A D B A B D D D A C C
二、填空题(本大题共4小题,每小题5分,共20分.将答案填在答题卡上的相应位置)
13. 7 14. 15. 16.
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤 )
17.解: (1)直三棱柱,面,,
又,,,,,
,面,.----------5分
(2)取的中点,连结和,
,且,
四边形为平行四边形,
,面,
,且,四边形为平行四边形,,面,
,面面,平面.----------10分
18.解: (1),又∵,∴......................6分
(2)由(1)知
............................ 10分
因为,所以当时,取得最大值.................................12分
19.解:(1)由an+1=2Sn+1可得an=2Sn﹣1+1(n≥2),两式相减得an+1﹣an=2an
即an+1=3an(n≥2).又a2=2S1+1=3,所以a2=3a1.故{an}是首项为1,公比为3的等比数列.
所以an=3n﹣1. ................................................................5分
(2)因为 ,所以.
则,
两式相减得:.
所以=............................................................12分
20. 解:(1)如图,连接,因为是的中点,是的中点,
所以在中,,
平面, 平面,
所以平面. -------------5分
(2)由等体积法,得,
因为是的中点,
所以点到平面的距离是点到平面的距离的一半.
如图,作交于点,由正三棱柱的性质可知,平面.
设底面正三角形的边长,则三棱锥的高, ------------9分
,
所以,解得,
所以该正三棱柱的底面边长为. -------------12分
21.解:(1)在中,.
所以,所以为直角三角形,. -------------3分
又因为平面,所以.
而,所以平面. -------------5分
(2)(方法一)如图延长,相交于,连接,
则平面平面.
二面角就是平面与平面所成二面角.
因为,所以是的中位线.
,这样是等边三角形.
取的中点为,连接,因为平面.
所以就是二面角的平面角. -------------10分
在,所以. -------------12分
(方法二)建立如图所示的空间直角坐标系,
可得.
.
设是平面的法向量,则
令得. -------------9分
取平面的法向量为. -------------10分
设平面与平面所成二面角的平面角为,
则,从而. -------------12分
22.解:(1)由题知,得直线AM的方程为,直线AN的方程为
所以,圆心到直线AM的距离,所以,,-------------3分
由题知,所以AN⊥AM,,-----------5分
(2)方法一:由题知直线AM的方程,直线AN的方程为
联立方程,所以,
得或 所以,-------------7分
同理,,-------------8分
所以直线为
即,得,
所以直线恒过定点.-------------12分
方法二:由知直线的斜率不为0,
设直线的方程为,
联立 得
且 -------------7分
,
又
即
-------------9分
化简整理得,解得或(舍去) -------------11分
直线的方程为,故直线恒过定点 -------------12分
同课章节目录
