二年级上册数学教案-6.7 整理与提高(数学广场-幻方) 沪教版
文档属性
| 名称 | 二年级上册数学教案-6.7 整理与提高(数学广场-幻方) 沪教版 |  | |
| 格式 | doc | ||
| 文件大小 | 48.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-29 12:27:45 | ||
图片预览

文档简介
教学设计方案
学科: 数学 课题: 幻方
一、教学目标 教学目标: 1.经历观察、猜想、计算验证的过程,主动探究幻方的重要特征,理解幻方。
2.能灵活运用幻方的特点进行判断及计算、填写幻方中所缺的数。
3.经历幻方特征的探究过程,发展观察、比较、归纳、逻辑推理等数学能力。
4.感受数学的悠久历史文化及其魅力,增强学数学的兴趣与好奇。
教学重点:初步认识幻方,发现幻和为15的幻方的特征。
教学难点:能运用规律巧妙地找出幻方中缺失的数。
二、制定依据:
教材分析:
《幻方》 这一教学内容被安排在了二年级上整理与提高单元中。幻方最早起源于我国,宋代数学家杨辉称之为纵横图。中国汉代已有三阶纵横图,称谓九宫。教材通过“大禹治水”的故事,引入龟背上的洛书——幻方。它是由1~n2个自然数组成的一个n阶数阵,它的各行各列及对角线上的n个数字之和都相等。
教材中只呈现了由数字1-9组成的幻方,因此,需引导学生思考、探究由数字1-9组成的幻方的特征。通过观察、比较,发现幻方的其它共同特征。通过幻方的特征,尝试寻找各种方法与策略计算填写完整幻方。意图进一步巩固和内化幻方的特征,达成知识系统整体建构的目的。
学情分析:
二年级学生有着强烈的好奇心,活泼好动,学习以兴趣占主导,适合采用故事、多媒体课件的“有声有色”、游戏和挑战性练习等教学方式渲染气氛,激发学习兴趣,长久保持旺盛的探究活力。
本课为数学广场的内容,对学生有一定的思维挑战性,如何让更多的孩子走进来,需要教师在教学设计中贯彻深入浅出的数学教学策略。通过探索幻方中的奥秘,在得到计算训练的同时,又感受数学研究的乐趣及数学的悠久文化和古代数学家的伟大发明。
幻方,一部分学生可能在课外接触过,有一定的基础,他们可以在探究幻方的特征时带动其他同学来研究幻方的秘密。多数学生对于幻方特点的描述及利用幻方的特点加以判断上存在困难。与此同时,对于寻找各种方法与策略计算填完整幻方,可能部分学生也存在困惑。因此,在整节课的教学中,对于幻方的特点描述加以了强调,对于计算填完整幻方的策略与方法进行了指导,以此来帮助学生更好地理解幻方。
教学过程
教学环节 对应目标 教师活动 学生活动 设计意图
评价关注点
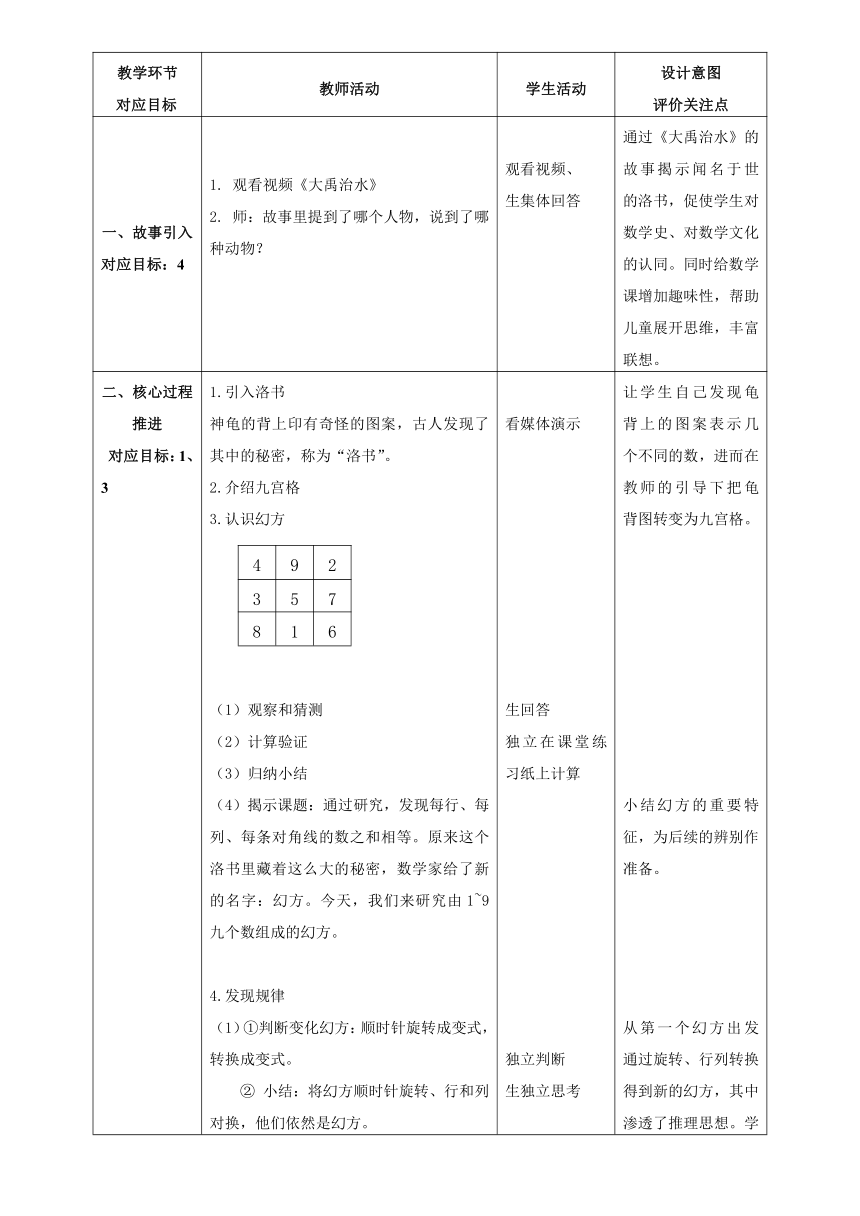
故事引入 对应目标:4 观看视频《大禹治水》
师:故事里提到了哪个人物,说到了哪种动物?
观看视频、
生集体回答 通过《大禹治水》的故事揭示闻名于世的洛书,促使学生对数学史、对数学文化的认同。同时给数学课增加趣味性,帮助儿童展开思维,丰富联想。
二、核心过程推进 对应目标:1、3
1.引入洛书
神龟的背上印有奇怪的图案,古人发现了其中的秘密,称为“洛书”。
2.介绍九宫格
3.认识幻方
4
9
2
3
5
7
8
1
6
观察和猜测
计算验证
归纳小结
(4)揭示课题:通过研究,发现每行、每列、每条对角线的数之和相等。原来这个洛书里藏着这么大的秘密,数学家给了新的名字:幻方。今天,我们来研究由1~9九个数组成的幻方。
4.发现规律
(1)①判断变化幻方:顺时针旋转成变式,转换成变式。
② 小结:将幻方顺时针旋转、行和列对换,他们依然是幻方。
(2)观察比较:观察你们小组四个人的幻方,你们发现有什么共同的特征?
(3)小结归纳:由1~9组成的幻方除了“每行、每列、每条对角线数之和是15”的特征之外,还有“5在中心,5两端的数之和是10;双数在角上,单数在中间”的特征。
看媒体演示
生回答
独立在课堂练习纸上计算
独立判断
生独立思考
小组讨论
全班汇报交流
观察、分析、比较、寻找幻方的联系与特征。
让学生自己发现龟背上的图案表示几个不同的数,进而在教师的引导下把龟背图转变为九宫格。
小结幻方的重要特征,为后续的辨别作准备。
从第一个幻方出发通过旋转、行列转换得到新的幻方,其中渗透了推理思想。学生通过自主探究观察比较找出特征,体现学生是学习的主体。
三、巩固练习 对应目标:2 1.判断:它们是和是15的幻方吗?
2.和全是15,填空
(1)填写幻方(空一格)
(2)填写幻方(空多格)
3.小结:拿到题目,我们要先观察,再想想幻方的特征,确定先填什么,再填什么,这样才能又快又好地完成任务。
师生互动
个别回答
在练习纸上独立完成 学生掌握知识后应能较好地解答问题,但如何灵活、快速、正确地解答也是教学难点,所以规律的运用就非常的重要。他们自己意识到从哪一步入手解答最简单,最快、最准确是关键。
拓展延伸 对应目标:4
辨析由数字2~10组成的九宫格是不是幻方。
小结:不仅1~9能组成幻方,我们把数换成2~10,也可以形成幻方。
2.介绍:不同形式的幻方。
3.介绍生活中的幻方
独立思考
认真倾听
运用材料,借用数与形的变换,拓宽视野,丰富对幻方的认识。
通过生活中的幻方,感受数学的趣味性。
总结 对应目标:梳理知识 今天我们一起研究了幻方,你有什么收获? 说说自己这节课学到的知识。
反思与重建
附
附板书设计:
幻方
每行、每列、每条对角线上的数之和相等。
学科: 数学 课题: 幻方
一、教学目标 教学目标: 1.经历观察、猜想、计算验证的过程,主动探究幻方的重要特征,理解幻方。
2.能灵活运用幻方的特点进行判断及计算、填写幻方中所缺的数。
3.经历幻方特征的探究过程,发展观察、比较、归纳、逻辑推理等数学能力。
4.感受数学的悠久历史文化及其魅力,增强学数学的兴趣与好奇。
教学重点:初步认识幻方,发现幻和为15的幻方的特征。
教学难点:能运用规律巧妙地找出幻方中缺失的数。
二、制定依据:
教材分析:
《幻方》 这一教学内容被安排在了二年级上整理与提高单元中。幻方最早起源于我国,宋代数学家杨辉称之为纵横图。中国汉代已有三阶纵横图,称谓九宫。教材通过“大禹治水”的故事,引入龟背上的洛书——幻方。它是由1~n2个自然数组成的一个n阶数阵,它的各行各列及对角线上的n个数字之和都相等。
教材中只呈现了由数字1-9组成的幻方,因此,需引导学生思考、探究由数字1-9组成的幻方的特征。通过观察、比较,发现幻方的其它共同特征。通过幻方的特征,尝试寻找各种方法与策略计算填写完整幻方。意图进一步巩固和内化幻方的特征,达成知识系统整体建构的目的。
学情分析:
二年级学生有着强烈的好奇心,活泼好动,学习以兴趣占主导,适合采用故事、多媒体课件的“有声有色”、游戏和挑战性练习等教学方式渲染气氛,激发学习兴趣,长久保持旺盛的探究活力。
本课为数学广场的内容,对学生有一定的思维挑战性,如何让更多的孩子走进来,需要教师在教学设计中贯彻深入浅出的数学教学策略。通过探索幻方中的奥秘,在得到计算训练的同时,又感受数学研究的乐趣及数学的悠久文化和古代数学家的伟大发明。
幻方,一部分学生可能在课外接触过,有一定的基础,他们可以在探究幻方的特征时带动其他同学来研究幻方的秘密。多数学生对于幻方特点的描述及利用幻方的特点加以判断上存在困难。与此同时,对于寻找各种方法与策略计算填完整幻方,可能部分学生也存在困惑。因此,在整节课的教学中,对于幻方的特点描述加以了强调,对于计算填完整幻方的策略与方法进行了指导,以此来帮助学生更好地理解幻方。
教学过程
教学环节 对应目标 教师活动 学生活动 设计意图
评价关注点
故事引入 对应目标:4 观看视频《大禹治水》
师:故事里提到了哪个人物,说到了哪种动物?
观看视频、
生集体回答 通过《大禹治水》的故事揭示闻名于世的洛书,促使学生对数学史、对数学文化的认同。同时给数学课增加趣味性,帮助儿童展开思维,丰富联想。
二、核心过程推进 对应目标:1、3
1.引入洛书
神龟的背上印有奇怪的图案,古人发现了其中的秘密,称为“洛书”。
2.介绍九宫格
3.认识幻方
4
9
2
3
5
7
8
1
6
观察和猜测
计算验证
归纳小结
(4)揭示课题:通过研究,发现每行、每列、每条对角线的数之和相等。原来这个洛书里藏着这么大的秘密,数学家给了新的名字:幻方。今天,我们来研究由1~9九个数组成的幻方。
4.发现规律
(1)①判断变化幻方:顺时针旋转成变式,转换成变式。
② 小结:将幻方顺时针旋转、行和列对换,他们依然是幻方。
(2)观察比较:观察你们小组四个人的幻方,你们发现有什么共同的特征?
(3)小结归纳:由1~9组成的幻方除了“每行、每列、每条对角线数之和是15”的特征之外,还有“5在中心,5两端的数之和是10;双数在角上,单数在中间”的特征。
看媒体演示
生回答
独立在课堂练习纸上计算
独立判断
生独立思考
小组讨论
全班汇报交流
观察、分析、比较、寻找幻方的联系与特征。
让学生自己发现龟背上的图案表示几个不同的数,进而在教师的引导下把龟背图转变为九宫格。
小结幻方的重要特征,为后续的辨别作准备。
从第一个幻方出发通过旋转、行列转换得到新的幻方,其中渗透了推理思想。学生通过自主探究观察比较找出特征,体现学生是学习的主体。
三、巩固练习 对应目标:2 1.判断:它们是和是15的幻方吗?
2.和全是15,填空
(1)填写幻方(空一格)
(2)填写幻方(空多格)
3.小结:拿到题目,我们要先观察,再想想幻方的特征,确定先填什么,再填什么,这样才能又快又好地完成任务。
师生互动
个别回答
在练习纸上独立完成 学生掌握知识后应能较好地解答问题,但如何灵活、快速、正确地解答也是教学难点,所以规律的运用就非常的重要。他们自己意识到从哪一步入手解答最简单,最快、最准确是关键。
拓展延伸 对应目标:4
辨析由数字2~10组成的九宫格是不是幻方。
小结:不仅1~9能组成幻方,我们把数换成2~10,也可以形成幻方。
2.介绍:不同形式的幻方。
3.介绍生活中的幻方
独立思考
认真倾听
运用材料,借用数与形的变换,拓宽视野,丰富对幻方的认识。
通过生活中的幻方,感受数学的趣味性。
总结 对应目标:梳理知识 今天我们一起研究了幻方,你有什么收获? 说说自己这节课学到的知识。
反思与重建
附
附板书设计:
幻方
每行、每列、每条对角线上的数之和相等。
同课章节目录
- 一、复习与提高
- 两位数加减法的复习
- 加与减
- 巧算
- 方框里填几
- 二、乘法、除法(一)
- 乘法引入
- 看图写乘法算式
- 倍
- 10的乘法
- 5的乘法
- 2的乘法
- 4的乘法
- 8的乘法
- 2、4、8的乘法之间的关系
- 分一分与除法
- 用乘法口诀求商
- 几倍
- 被除数为0的除法
- 小练习(一)
- 三、统计
- 统计表初步
- 条形统计图(一)
- 四、乘法、除法(二)
- 7的乘、除法
- 3的乘、除法
- 6的乘、除法
- 9的乘、除法
- 3、6、9的乘法之间的关系
- “九九”——乘法口诀表
- 看图编乘、除法问题
- 分拆为乘与加
- 有余数的除法
- 有余数除法的计算
- 小练习(二)
- 五、几何小实践
- 角与直角
- 正方体、长方体的初步认识
- 长方形、长方形的初步认识
- 六、整理与提高
- 大家来做乘法
- 乘除大游戏
- 5个3加3个3等于8个3
- 5个3减3个3等于2个3
- 乘与除
- 数学广场——点图与数
- 数学广场——幻方
- 数学广场——从不同方向观察物体
