专题24.1 圆的有关性质-2020-2021数学九上册同步课堂帮帮帮(含解析)
文档属性
| 名称 | 专题24.1 圆的有关性质-2020-2021数学九上册同步课堂帮帮帮(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-30 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第24章 圆
24.1 圆的有关性质
1.圆
在一个平面内,一条线段OA绕它的一个端点O旋转一周,另一个端点A所形成的图形叫作______________.21教育网
圆心:固定的端点叫作圆心.
半径:线段OA的长度叫作这个圆的______________.
圆的表示方法:以点O为圆心的圆,记作“______________”,读作“圆O”.
同时从圆的定义中归纳:
(1)圆上各点到定点(圆心)的距离都等于定长(半径);
(2)到定点的距离等于定长的点都在同一个圆上.
圆的第二定义:所有到定点的距离等于定长的点组成的图形叫作圆.
2.垂直于弦的直径
(1)圆是轴对称图形,任何一条直径所在的直线都是它的________________,圆有_______________条对称轴.21·cn·jy·com
(2)垂直于弦的______________平分弦,并且平分弦所对的弧;平分弦(不是直径)的直径__________于弦,并且________________弦所对的弧.
3.弧、弦、圆心角
(1)顶点在圆心的角叫做_______________.
(2)在同圆或等圆中,相等的圆心角所对的弧________________,所对的弦也________________.
(3)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等.
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧也相等.
4.圆周角
(1)圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.
特征:①角的顶点在圆上;②角的两边都与圆相交.
(2)同弧所对的圆周角的度数没有变化,并且它的度数恰好等于这条弧所对的圆心角的度数的___________.
(3)在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的_______________.
(4)半圆(或直径)所对的圆周角是_____________,90°的圆周角所对的弦是_______________.
(5)如果一_????¤?è???????????_有顶点都在同一个圆上,这个多边形叫做_____________,这个圆叫做这个多边形的外接圆.圆内接四边形的______________.
1.圆 半径 ⊙O
2.(1)对称轴 无数 (2)直径 垂直 平分
3.(1)圆心角 (2)相等 相等
4.(2)一半 (3)一半 (4)直角 直径 (5)圆内接多边形 对角互补
帮—重点 垂径定理及其推论,圆周角定理及其推论
帮—难点 圆的有关概念、圆心角、圆周角的概念
帮—易错 弧、弦、圆心角的关系
一、圆的有关概念
圆中容易混淆的“两组基本概念”
1.弦与直径:(1)弦是连接圆上任意两点的线段,直径是经过圆心的弦.
(2)直径是弦,是圆中最长的弦,但弦不一定是直径.
2.弧与半圆:
(1)圆上任意两点分圆成两段弧,圆上任意一条直径的两个端点把圆分成两条孤,每一条弧叫作半圆.
(2)半圆是弧,但弧不一定是半圆.
下列说法:①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,但弧不一定是半圆.正确的说法有( )【来源:21·世纪·教育·网】
A.1个 B.2个 C.3个 D.4个
【答案】C
【解析】
【分析】
利用圆的有关定义及性质分别进行判断后即可确定正确的选项.
【详解】
①直径是弦,正确,符合题意;
②弦不一定是直径,错误,不符合题意;
③半径相等的两个半圆是等弧,正确,符合题意;
④能够完全重合的两条弧是等弧,原命题错误,不符合题意;
⑤半圆是弧,但弧不一定是半圆,正确,符合题意;
正确的有3个,
故选:C.
【点睛】本题考查了圆的认识及圆的有关定义,解题的关键是了解圆的有关概念,难度不大.
二、垂径定理及其推论的有关计算与证明
垂径定理应用中常作的辅助线:
(1)若已知圆心和弦,则连接圆心和弦的一个端点,即“连半径”,并作垂直于弦的直径,构造直角三角形;
(2)若已知圆心和弦(弧)的中点,则连接圆心和弦(弧)的中点,并延长使其与圆相交,得圆的直径,再“连半径”,构造直角三角形.
如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC、BC为直径作半圆,其中M,N分别是AC、BC为直径作半圆弧的中点,,的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )
A.17 B.18 C.19 D.20
【答案】C
【解析】
【分析】
连接OP,OQ,根据M,N分别是AC、BC为直径作半圆弧的中点,,的中点分别是P,Q.得到OP⊥AC,OQ⊥BC,从而得到H、I是AC、BC的中点,利用中位线定理得到OH+OI=(AC+BC)=13和PH+QI=6,从而利用AB=OP+OQ=OH+OI+PH+QI求解.
【详解】
连接OP,OQ,分别交AC,BC于H,I,
∵M,N分别是AC、BC为直径作半圆弧的中点,,的中点分别是P,Q,
∴OP⊥AC,OQ⊥BC,由对称性可知:H,P,M三点共线,I,Q,N三点共线,
∴H、I是AC、BC的中点,
∴OH+OI=(AC+BC)=13,
∵MH+NI=AC+BC=13,MP+NQ=7,
∴PH+QI=13﹣7=6,
∴AB=OP+OQ=OH+OI+PH+QI=13+6=19,
故选C.
【点睛】本题考查了中位线定理的应用,解题的关键是正确作出辅助线,题目中还考查了垂径定理和轴对称的知识,有难度.
三、应用垂径定理作图
圆弧中点的确定:由垂径定理可知垂直于弦的直径平分弦,并且平分弦所对的两条弧,所以常通过作孤所对的弦的垂直平分线确定孤的中点.
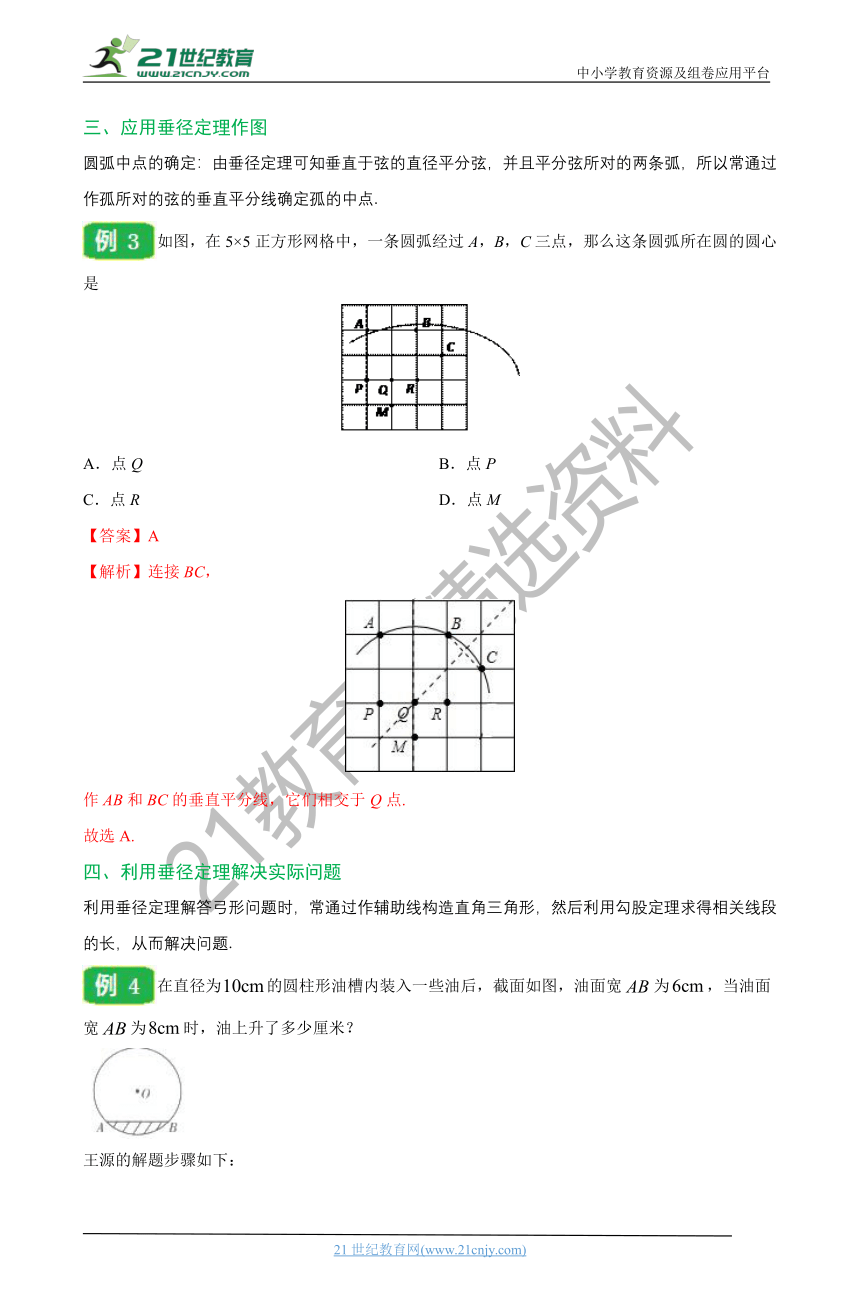
如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是
A.点Q B.点P
C.点R D.点M
【答案】A
【解析】连接BC,
作AB和BC的垂直平分线,它们相交于Q点.
故选A.
四、利用垂径定理解决实际问题
利用垂径定理解答弓形问题时,常通过作辅助线构造直角三角形,然后利用勾股定理求得相关线段的长,从而解决问题.【版权所有:21教育】
在直径为的圆柱形油槽内装入一些油后,截面如图,油面宽为,当油面宽为时,油上升了多少厘米?
王源的解题步骤如下:
[解]连接,过点作于点.
于点,且为弦,.
当时,在中,.
当时,在中,.
.即油上升了.
请问王源的解题过程正确吗?如果不正确,请写出正确的解题步骤.
【答案】王源的解题过程不正确.正确解题步骤见解析.油上升了或.
【解析】
【分析】
连接AO,过点O作OC⊥AB于点C,根据垂径定理结合勾股定理求出当AB=6cm和8cm时OC的长度,即可得出结论.
【详解】
王源的解题过程不正确.正确解题步骤如下:
连接,过点作于点,如图所示.
∵于点,且为弦,.
当时,在中,,;
当时,在中,.
或.
答:油上升了或.
【点睛】本题主要考查了垂径定理以及勾股定理,解题的关键是求出OC的长,根据OC的变化来得出结论.
五、利用圆周角定理及其推论求角的度数
计算圆心角和_?????¨è§?????????¨_意事项:
1.在进行有关圆心角与圆周角的计算时,应适当添加辅助线,以方便角度之间的转化.一条弧所对的圆心角只有一个,而所对的圆周角有无数个,它们都相等;
2.一条弦所对的圆心角只有一个,但它所对的圆周角却有无数个,在同一条弦的同侧的圆周角相等,在同一条弦的异侧的两个圆周角互补.
如图,在的外接圆上,所对的圆心角的度数比为.在上取一点,过分别作直线的平行线,交于两点,则的度数为( )
A.55° B.60° C.65° D.70°
【答案】C
【解析】
【分析】
根据题意即可求出所对的圆心角的度数,然后根据圆周角定理即可求出∠BAC的度数,再根据平行线的性质即可证出,最后根据三角形的内角和定理即可求出结论.
【详解】
解:所对的圆心角的度数比为
所对的圆心角的度数为
.
故选C.
【点睛】此题考查的是圆周角定理、平行线的性质和三角形的内角和定理,掌握圆周角定理、平行线的性质和三角形的内角和定理是解决此题的关键.
六、运用弧、弦、圆心角、圆周角的关系进行证明
圆中证明弧、弦、圆心角、圆周角相等或倍分关系的方法:
在圆中证明弧、弦、圆心角、圆周角_??????????????????_关系时,应从同类型元素(指弧、弦、角)的相等或倍分关系入手,转化为另一种元素的相等或倍分关系,从而得到问题的结论.
如图,以平行四边形的顶点为圆心,长为半径作,分别交于两点,交的延长线于点.
(1)求证:;
(2)连接,若,求的度数.
【答案】(1)详见解析;(2)70°
【解析】
【分析】
(1)通过平行四边形的对边平行,得到同位角和内错角相等,再利用等腰△ABE的两底角相等进行等量代换,进行求证;www-2-1-cnjy-com
(2)通过邻补角求得等腰△ABE的顶角∠BAE读数,再利用三角形内角和求底角∠B,平行四边形对角相等可求出∠D.
【详解】
(1)
证明:连接.
∵四边形是平行四边形,
,
,,
,
,
,
.
(2)解:为的直径,,
,
,
∵四边形是平行四边形,
.
【点睛】在圆的证明和计算中,证明两弧相等,常常需要构造弧所对的圆心角,通过证明圆心角相等来再进一步证明弧相等.
七、圆内接四边形
如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是
A.50° B.60°
C.80° D.100°
【答案】D
【解析】圆上取一点A,连接AB,AD,
∵点A、B,C,D在⊙O上,∠BCD=130°,∴∠BAD=50°,∴∠BOD=100°.
故选D.
八、圆中计算防漏解
已知圆的半径为13 cm,两弦AB∥CD,AB=24 cm,CD=10 cm,则两弦AB,CD间的距离是
A.7 cm B.17 cm
C.12 cm D.7 cm或17 cm
【易错提示】本题应分两种情况解答:(1)两弦在圆心的同侧;(2)两弦在圆心的异侧,易遗漏两弦在圆
心的异侧时的情况.
【正解】第一种情况:两弦在圆心的同侧时,如图,过点O作OE⊥弦CD,交CD于点E,交AB于点F.
∵AB∥CD,∴EF⊥AB,∴线段EF的长是AB,CD间的距离.
∵CD=10 cm,∴DE=5 cm.
∵OD=13 cm,∴由勾股定理可得OE=12 cm.
同理可求OF=5 cm,∴EF=OE?OF=7 cm.
第二种情况:两弦在圆心的异侧时,如图,过点O作OE⊥CD于点E,延长EO交AB于点F.
∵CD∥AB,∴EF⊥AB.∴线段EF的长是AB,CD间的距离,
∴EF=OE+OF=17 cm.故选D.
九、对圆心角与圆周角的性质理解不透彻
判断:(1)相等的圆心角所对的弧相等,所对的弦相等.( )
(2)相等的圆周角所对的弧相等.( )
【易错提示】误以为这两个题均是正确的.如图①,在同心圆中,∠AOB=∠COD,但即.
在图②中,与有公共点M,显然圆周角∠AMB=∠CMD,而.
【正解】(1)错误;(2)错误.
十、求圆周角时未分类讨论而漏解
如图,∠AOB=100°,点C在⊙O上,且点C不与A、B重合,则∠ACB的度数为
A.50° B.80°或50°
C.130° D.?50°或130°
【易错提示】点C可能在优弧上也可能在劣弧上,此题应分两种情况进行讨论.
【正解】①如图所示,当C点在优弧上时,因为∠AOB=100°,根据同弧所对圆周角是圆心角的一半,所以∠ACB=∠AOB=50°.
②如图所示,当C点在劣弧上时,
因为∠AOB=100°,所以优弧所对的圆心角为:360°?100°=260°,
根据同弧所对圆周角是圆心角的一半,所以∠ACB=130°.
综上所述,∠ACB的度数为50°或130°.
故选D.
一、单选题
1.已知点在线段上(点与点不重合),过点的圆记为圆,过点的圆记为圆,过点的圆记为圆,则下列说法中正确的是( )
A.圆可以经过点 B.点可以在圆的内部
C.点可以在圆的内部 D.点可以在圆内部
【答案】B
【解析】
【分析】
根据题意,画出符合题意的示意图,然后求解.
【详解】
解:∵点在线段上(点与点不重合),过点的圆记为圆,∴点可以在圆的内部,故A错误,B正确;∵过点的圆记为圆,∴点可以在圆的外部,故C错误;∵过点的圆记为圆,∴点可以在圆的外部,故D错误.
故选B.
【点睛】本题考查点与圆的位置关系,画出适当的辅助图形,采用数形结合的方法,更有助于解题.
2.如图,点A,B,C都在⊙O上,∠ABC=70°,则∠AOC的度数是( )
A.35° B.70° C.110° D.140°
【答案】D
【解析】
【分析】
根据圆周角定理问题可解.
【详解】
解:∵∠ABC所对的弧是,
∠AOC所对的弧是,
∴∠AOC=2∠ABC=2×70°=140°.
故选D.
【点睛】本题考查圆周角定理,解答关键是掌握圆周角和同弧所对的圆心角的数量关系.
3.如图,图中的弦共有( )
A.1条 B.2条 C.3条 D.4条
【答案】B
【解析】
【分析】
根据弦的定义解答即可.
【详解】
解:图形中有弦AB和弦CD,共2条,
故选B.
【点睛】本题考查弦的定义,熟记弦的定义是解题的关键.
4.下列说法错误的是( )
A.圆内接四边形的对角互补 B.圆内接四边形的邻角互补
C.圆内接平行四边形是矩形 D.圆内接梯形是等腰梯形
【答案】B
【解析】
【分析】
根据圆内接四边形的性质分别分析得出即可.
【详解】
解:A、圆内接四_è???????????è§????_补,正确,不合题意;
B、圆内接四边形的邻角互补,错误,符合题意;
C、圆内接平行四边形是矩形,正确,不合题意;
D、圆内接梯形是等腰梯形,正确,不合题意.
故选:B.21*cnjy*com
【点睛】此题主要考查了圆内接四边形的性质,正确把握圆内接四边形对角互补进而得出是解题关键.
二、填空题
5.如图,是⊙O的直径,交⊙O于点交⊙O于点,给出以下结论:①;②;③;④.其中正确结论的序号是_________.
【答案】①②③
【解析】
【分析】
①根据圆周角定理,同弧所对的圆周角等于其所对的圆心角的一半,②根据直径所对的圆周角是判断,③同一个圆中,圆周角相等,弧相等,④根据等腰直角三角形的判断方法判定.
【详解】
解:如图,连接.是的直径,.又,故②正确.是的平分线,.故③正确.是的直径,..是的直角边,是斜边,.故④错误.由圆周角定理知,,故①正确.
综上,正确的结论是①②③.
【点睛】本题考查直径所对的圆周角是、等腰三角形的性质、角平分线的性质、圆周角定理等,知识综合性较强,是常见考点,难度一般,熟练掌握相关知识是解题关键.
6.在同一个_??????,_??????_心角不超过180°时, 圆心角越大, 所对的弧______;所对的弦__________, 所对弦的弦心距____________.
【答案】越长 越长 越短
【解析】
【分析】
根据圆心角定理解答即可.
【详解】
在同一个圆中, 当圆心角不超过180°时, 圆心角越大, 所对的弧越长,所对的弦越长,所对弦的弦心距越短.
故答案为越长;越长;越短.
【点睛】本题考查了圆心角定理及其推理,解此题的关键在于熟练掌握其知识点.
7.如图,分别以四边形ABCD(边长均大于4)的四个顶点为圆心,2为半径画圆,则图中四个阴影部分的面积之和是________.
【答案】4π
【解析】
【分析】
根据平行四边形的内角和等于360°可知,图中阴影部分的面积正好等于一个圆的面积,然后根据圆的面积公式列式计算即可得解.
【详解】
解:∵平行四边形ABCD的边长均大于4,各弧的半径都是2,
∴图中阴影部分的面积等于一个圆的面积,
即π?22=4π.
故答案为4π.
【点睛】本题考查了平行四边形的内角和等于360°的性质,判断出阴影部分的面积等于一个圆的面积是解题的关键.
8.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积(弦×矢+矢2).孤田是由圆弧和其所对的弦围成(如图中的阴影部分),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,运用垂径定理(当半径⊥弦时,平分)可以求解.现已知弦米,半径等于5米的弧田,按照上述公式计算出弧田的面积为_____平方米.
【答案】10
【解析】
【分析】
根据垂径定理得到,由勾股定理得到,求得,根据弧田面积(弦×矢+矢2)即可得到结论.
【详解】
解:∵弦米,半径弦,
∴,
∴,
∴,
∴弧田面积(弦×矢+矢2),
故答案为10
【点睛】此题考查垂径定理的应用,关键是根据垂径定理和扇形面积解答.
三、解答题
9.如图,已知E是⊙O上任意一点,CD平分∠ACB,求证:ED平分∠AEB.
【答案】见解析.
【解析】
【分析】
根据CD平分∠ACB,判断出,再根据弧相等,判断出∠AED=∠BED即可.
【详解】
∵平分,
∴,
∴
∴ED平分∠AEB.
【点睛】本题考查了圆周角定理,根据同弧所对的圆周角相等解答.
10.如图,在⊙O中,AB.AC是弦,,求的关系.
【答案】
【解析】
【分析】
过A作⊙O的直径,交⊙O于D,分别在等腰△OAB、等腰△OAC中,根据三角形外角的性质即可求出答案.
【详解】
过A作⊙O的直径,交⊙O于D;
中,,则,
同理可得:,
∵,
∴.
【点睛】本题考查了等腰三角形的性质及三角形的外角性质,正确添加辅助线是解题的关键.
一、单选题
1.如图,在中,已知AB=CD,则AC与BD的关系是( )
A. B. C. D.不确定
【答案】A
【解析】
【分析】
根据已知条件可得,进而可得,根据圆心角、弧、弦的关系即可得
.
【详解】
,
,
,
故选:A.
【点睛】本题主要考查圆心角、弧、弦的关系,熟练掌握圆的性质是解题关键.
2.如图,在圆O中,弦AB=4,点C在AB上移动,连接OC,过点C作CD⊥OC交圆O于点D,则CD的最大值为 ( )
A. B.2 C. D.
【答案】B
【解析】
【分析】
连接OD,利用勾股定理得到CD,利用垂线段最短得到当OC⊥AB时,OC最小,根据垂径定理计算即可.
【详解】
连接OD,如图,设圆O的半径为r,
∵CD⊥OC,
∴∠DCO=90°,
∴CD=,
∴当OC的值最小时,CD的值最大,而OC⊥AB时,OC最小,
此时D、B重合,则由垂径定理可得:CD=CB=AC=AB=2,
∴CD的最大值为2.
故答案为:2.
【点睛】本题考查垂径定理和勾股定理,作辅助线构造直角三角形应用勾股定理,并熟记垂径定理内容是解题的关键.
3.如图,AB是⊙O的直径,BC是弦,点P是劣弧(含端点)上任意一点,若AB=5,BC=4,则AP的长不可能是( )
A.2 B.3 C.4 D.5
【答案】A
【解析】
【分析】
连接AC,如图,利用圆周角定理得到∠ACB=90°,利用勾股定理得到AC=3,则3≤AP≤5,然后对各选项进行判断.
【详解】
解:连接AC,如图,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴AC===3,
∵点P是劣弧(含端点)上任意一点,
∴AC≤AP≤AB,
即3≤AP≤5.
故选A.
【点睛】本题考查_????????¨è§???????_:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
二、填空题
4.如图,已知点经过原点,交轴正半轴于点.点在上,,圆心的坐标为__________.
【答案】
【解析】
【分析】
连接OP,OB,PB,延长BP交⊙P于E,连接OE,作EF⊥OA于F,BH⊥x轴于H.利用全等三角形的性质求出点E坐标即可解决问题.
【详解】
解:连接OP,OB,PB,延长BP交⊙P于E,连接OE,作EF⊥OA于F,BH⊥x轴于H.
∵∠BPO=2∠BAO,∠BAO=45°,
∴∠BPO=90°,
∵PO=OB,
∴△PBO是等腰直角三角形,
∵BE是直径,
∴∠BOE=90°,
∴∠OBE=∠OEB=45°,
∴OE=OB,
∵∠EOB=∠AOH=90°,
∴∠EOF=∠BOH,
∵∠EFO=∠BHO=90°,
∴△EFO≌△BHO(AAS),
∴OF=OH=5,EF=BH=2,
∴E(?2,5),
∵PE=PB,
∴P.
故答案为.
【点睛】本题考查圆周角定_????????¨??????è§?_形的判定和性质,等腰直角三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
5.如图,点A,B,D在⊙O上,∠A=25°,OD的延长线交直线BC于点C,且∠OCB=________,则直线BC与⊙O的位置关系为
【答案】40°
【解析】
【分析】
先根据直线BC与⊙O相切,得到∠OBC=90°,再利用同弧所对的圆周角与圆心角的关系求出∠BOC=2∠A=50°,可求出∠OCB=40°.
【详解】
∵直线BC与⊙O相切,
∴∠OBC=90°,
∵∠BOC=2∠A=50°,
∴∠OCB=40°,答案为:40°.
【点睛】本题考查了同弧所对的圆周角与圆心角的关系,及圆的切线的性质,关键是熟练掌握这些性质.
6.如图,半圆形纸片AMB_????????????1__cm,用如图所示的方法将纸片对折,使对折后半圆弧的中点M与圆心O重合,则折痕CD的长为________ .
【答案】cm
【解析】
【分析】
作MO交CD于E,则MO⊥CD.连接CO.根据勾股定理和垂径定理求解.
【详解】
作MO交CD于E,则MO⊥CD,连接CO,
对折后半圆弧的中点M与圆心O重合,
则ME=OE=OC,
在直角三角形COE中,CE=,
折痕CD的长为2×=(cm).
故答案为:cm
【点睛】作出辅助线,构造直角三角形,根据对称性,利用勾股定理解答.
三、解答题
7.如图,过的直径上两点,分别作弦,.
求证:(1);
(2).
【答案】(1)详见解析;(2)详见解析
【解析】
【分析】
(1)连接OC、OF,根据圆_???è§??????§??????_的关系即可得到结论;
(2)根据等腰三角形的性质得到∠A=∠OCA=∠BFC=∠B,等量代换得到∠BFC=∠ACF.根据平行线的性质得到∠AMC=∠ANE.根据全等三角形的性质即可得到结论.
【详解】
解:(1)如图,连接.
,
.
.
(2)
,
.
.
又.
.
在和中,
.
【点睛】本题考查了圆心角、弧、弦的关系,全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.【出处:21教育名师】
8.如图,已知为⊙O的直径且,点(不与重合)为⊙O上一个动点,线段经过点,且为⊙O上一点,的延长线与的延长线交于点.
(1)求证:;
(2)当点在⊙O上移动时,求四边形的最大面积.
【答案】(1)见解析;(2)8
【解析】
【分析】
(1)连接D_F???AF???é??_先证明四边形ADFE是矩形,推出EF=AD,即可解决问题.
(2)证明四边形EFCD是平行四边形,推出S矩形EFDA=S平行四边形EFCD,推出矩形EFDA的面积最大时,四边形EFCD的面积最大.
【详解】
(1)证明:连接DF,AF.
∵DE是直径,
∴∠EAD=90°,
∵FE⊥AB,
∴∠FEA=90°,
∴AF是直径,
∴∠ADF=90°,
∴∠FEA=∠EAD=∠ADF=90°,
∴四边形ADFE是矩形,
∴EF=AD,
∵EB=EA,∠BEF=∠EAD=90°,
∴△EFB≌△ADE(HL);
(2)解∵四边形ADFE是矩形,
∴EF∥AC,EF=AD,
∵BE=AE,
∴BF=CF,
∴AC=2EF,
∴EF=AD=CD,
∵EF∥CD,
∴四边形EFCD是平行四边形,
∵AD=CD,EF∥AC,
∴S矩形EFDA=S平行四边形EFCD,
∴矩形EFDA的面积最大时,四边形EFCD的面积最大,
当AF⊥DE时,矩形EFDA的面积最大,即矩形EFDA为正方形时,面积最大,
此时矩形EFDA的面积的最大值.
∴四边形FCDE的最大面积为8.
【点睛】本题考查了全等_???è§?????????¤???_和性质,圆周角定理,平行四边形的判定和性质,矩形的判定和性质,正方形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
9.说出下列点的轨迹是什么图形,并画出图形.
(1)在平面直角坐标系内,到x轴,y轴距离相等的点的轨迹.
(2)以已知点A为端点的线段AB=10cm,这线段的另一个端点的轨迹.
(3)已知直线上有两点A、B,且AB=3cm,与A、B构成面积为3cm2的三角形的点的轨迹.
【答案】(1)x轴、y轴所构成的四个角的平分线;(2)以点A为圆心,半径长为10cm的圆;(3)平行于直线且与直线的距离为的两条直线.
【解析】
【分析】
(1)根据角平分线的性质即可得答案;(2)根据圆的定义即可得答案;(3)根据等底等高的三角形面积相等,平行线间的距离相等的性质即可得答案.【来源:21cnj*y.co*m】
【详解】
(1)如图:∵角平分线上的点到角两边的距离相等,
∴在平面直角坐标系内,到x轴,y轴距离相等的点的轨迹是x轴、y轴所构成的四个角的平分线;
(2)如图,∵到定点的距离为定长的点的轨迹是以定点为圆心,定长为半径的圆,
∴点A为端点的线段AB=10cm,另一个端点B的轨迹为以点A为圆心,半径长为10cm的圆,
(3)如图,∵AB=3cm,与A、B构成面积为3cm2,
∴AB边的高为2cm,
∵等底等高的三角形面积相等,平行线间的距离相等,
∴另一个点的轨迹为平行于直线且与直线的距离为的两条直线.
【点睛】本题考查的是点的轨迹,熟练掌握角平分线的性质、圆的定义及平行线的性质是解题关键.
10.如图,B_C?????????O???_直径,点P是半圆弧的中点,点A是弧BP的中点,AD⊥BC于D,连结AB、PB、AC,BP分别与AD、AC相交于点E、F.
(1)求证:AE=BE;
(2)判断BE与EF是否相等吗,并说明理由;
(3)小李通过操作发现CF=2AB,请问小李的发现是否正确?若正确,请说明理由;若不正确,请写出CF与AB正确的关系式.
【答案】(1)见解析;(2)BE=EF,理由见解析;(3)小李的发现是正确的,理由见解析
【解析】
【分析】
(1)如图1,连_???AP?????±B_C是半⊙O的直径,AD⊥BC于D,得到∠ACB+∠ABC=∠BAD+∠ABD=90°,于是得到∠ACB=∠BAD,根据圆周角定理得到∠P=∠ACB=∠ABP,即可求出结论;
(2)根据圆周角定理求出∠ABE=∠BAE,求出AE=BE,求出∠CAD=∠AFB,求出AE=EF,即可得出答案;
(3)根据全等三角形的性质和判定求出BG=CF,AB=AG,即可得出答案.
【详解】
(1)如图1,连接AP,
∵BC是半⊙O的直径,
∴∠BAC=90°,
∵AD⊥BC于D,
∴∠ADB=90°,
∴∠ACB+∠ABC=∠BAD+∠ABD=90°,
∴∠ACB=∠BAD,
∵点A是弧BP的中点,
∴∠P=∠ACB=∠ABP,
∴∠ABE=∠BAE,
∴AE=BE;
(2)BE=EF,
理由是:∵BC是直径,AD⊥BC,
∴∠BAC=∠ADC=90°,
∴∠BAD=∠ACB,
∵A为弧BP中点,
∴∠ABP=∠ACB,
∴∠BAD=∠ABP,
∴BE=AE,∠FAD=∠AFB,
∴EF=AE,
∴BE=EF;
(3)小李的发现是正确的,
理由是:如图2,延长BA、CP,两线交于G,
∵P为半圆弧的中点,A是弧BP的中点,
∴∠PCF=∠GBP,∠CPF=∠BPG=90°,BP=PC,
在△PCF和△PBG中,
,
∴△PCF≌△PBG(ASA),
∴CF=BG,
∵BC为直径,
∴∠BAC=90°,
∵A为弧BP中点,
∴∠GCA=∠BCA,
在△BAC和△GAC中,
∴△BAC≌△GAC(ASA),
∴AG=AB=BG,
∴CF=2AB.
【点睛】本题考查_????????¨è§???????_,圆心角、弧、弦之间的关系,全等三角形的性质和判定等知识点的应用,主要考查学生综合运用性质进行推理和计算的能力,题目综合性比较强,有一定的难度.
一、单选题
1.(2020·浙_?±?????·??·???è??_真题)如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E.设∠AED=α,∠AOD=β,则( )
A.3α+β=180° B.2α+β=180° C.3α﹣β=90° D.2α﹣β=90°
【答案】D
【解析】
【分析】
根据直角三角形两锐角互余性质,用α表示∠CBD,进而由圆心角与圆周角关系,用α表示∠COD,最后由角的和差关系得结果.2-1-c-n-j-y
【详解】
解:∵OA⊥BC,
∴∠AOB=∠AOC=90°,
∴∠DBC=90°﹣∠BEO
=90°﹣∠AED
=90°﹣α,
∴∠COD=2∠DBC
=180°﹣2α,
∵∠AOD+∠COD=90°,
∴β+180°﹣2α=90°,
∴2α﹣β=90°,
故选:D.
【点睛】本题考查了圆周角定理以及直角三角形的两个锐角互余的关系,熟练掌握圆周角定理是解决本题的关键.
2.(2020·湖北武汉·中考真题)如图,在半径为3的⊙O中,是直径,是弦,是的中点,与交于点.若是的中点,则的长是( )
A. B. C. D.
【答案】D
【解析】
【分析】
连接DO、DA、DC,_è??DO???AC_交于点H,证明△DHE≌△BCE,得到DH=CB,同时OH是三角形ABC中位线,设OH=x,则BC=2x=DH,故半径DO=3x,解出x,最后在Rt△ACB中由勾股定理即可求解.
【详解】
解:连接DO、DA、DC、OC,设DO与AC交于点H,如下图所示,
∵D是的中点,∴DA=DC,∴D在线段AC的垂直平分线上,
∵OC=OA,∴O在线段AC的垂直平分线上,
∴DO⊥AC,∠DHC=90°,
∵AB是圆的直径,∴∠BCA=90°,
∵E是BD的中点,∴DE=BE,且∠DEH=∠BEC,
∴△DHE≌△BCE(AAS),
∴DH=BC,
又O是AB中点,H是AC中点,
∴HO是△ABC的中位线,
设OH=x,则BC=DH=2x,
∴OD=3x=3,∴x=1,
即BC=2x=2,
在Rt△ABC中,.
故选:D.
【点睛】本题考查了圆周角定理、三角形全等、勾股定理等,属于综合题,熟练掌握其性质和定理是解决此题的关键
3.(2020·浙江嘉兴·中考真题)如图,在等腰△ABC中,AB=AC=2,BC=8,按下列步骤作图:
①以点A为圆心,适当的长度为半径作弧,分别交AB,AC于点E,F,再分别以点E,F为圆心,大于EF的长为半径作弧相交于点H,作射线AH;
②分别以点A,B为圆心,大于AB的长为半径作弧相交于点M,N,作直线MN,交射线AH于点O;
③以点O为圆心,线段OA长为半径作圆.
则⊙O的半径为( )
A.2 B.10 C.4 D.5
【答案】D
【解析】
【分析】
如图,设OA交BC于T.解直角三角形求出AT,再在Rt△OCT中,利用勾股定理构建方程即可解决问题.21·世纪*教育网
【详解】
解:如图,设OA交BC于T.
∵AB=AC=2,AO平分∠BAC,
∴AO⊥BC,BT=TC=4,
∴AE=,
在Rt△OCT中,则有r2=(r﹣2)2+42,
解得r=5,
故选:D.
【点睛】本题考查作图——复杂作图,等腰三角形的性质,垂径定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.www.21-cn-jy.com
二、填空题
4.(2020·宁夏中考真题)我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”意思是:今有一圆柱形木材,埋在墙壁中,不知其大小.用锯去锯这木材,锯口深寸,锯道长尺(1尺寸).问这根圆形木材的直径是______寸.2·1·c·n·j·y
【答案】26
【解析】
【分析】
根据题意可得,由垂径定理可得尺寸,设半径,则,在中,根据勾股定理可得:,解方程可得出木材半径,即可得出木材直径.
【详解】
解:由题可知,
为半径,
尺寸,
设半径,
,
在中,根据勾股定理可得:
解得:,
木材直径为26寸;
故答案为:26.
【点睛】本题考查垂径定理结合_???è????????è?????_半径长度.如果题干中出现弦的垂线或者弦的中点,则可验证是否满足垂径定理;与圆有关的题目中如果求弦长或者求半径直径,也可以从题中寻找是否有垂径定理,然后构造直角三角形,用勾股定理求解.
5.(2018·海南中考真题_??????????????¨???_面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为_____.
【答案】(2,6)
【解析】
【分析】
此题涉及的知识点是平面直角坐标系_????????§è?¨??????_合应用.过点M作MF⊥CD于F,过C作CE⊥OA于E,在Rt△CMF中,根据勾股定理即可求得MF与EM,进而就可求得OE,CE的长,从而求得C的坐标.21cnjy.com
【详解】
∵四边形OCDB是平行四边形,点B的坐标为(16,0),
CD∥OA,CD=OB=16,
过点M作MF⊥CD于F,则
过C作CE⊥OA于E,
∵A(20,0),
∴OA=20,OM=10,
∴OE=OM?ME=OM?CF=10?8=2,
连接MC,
∴在Rt△CMF中,
∴点C的坐标为(2,6).
故答案为(2,6).
【点睛】此题重点考察学生对坐标与图形性质的实际应用,勾股定理,注意数形结合思想在解题的关键.
6.(2018·_é??é???±????????·_中考真题)如图,一下水管道横截面为圆形,直径为100cm,下雨前水面宽为60cm,一场大雨过后,水面宽为80cm,则水位上升______cm.21世纪教育网版权所有
【答案】10或70
【解析】
【分析】
分水位在圆心下以及圆心上两种情况,画出符合题意的图形进行求解即可得.
【详解】
如图,作半径于C,连接OB,
由垂径定理得:=AB=×60=30cm,
在中,,
当水位上升到圆心以下时??水面宽80cm时,
则,
水面上升的高度为:;
当水位上升到圆心以上时,水面上升的高度为:,
综上可得,水面上升的高度为30cm或70cm,
故答案为:10或70.
【点睛】本题考查了垂径定理的应用,掌握垂径定理、灵活运用分类讨论的思想是解题的关键.
三、解答题
7.(2020·江苏泰州·中考真题)如图,在中,点为的中点,弦、互相垂直,垂足为,分别与、相交于点、,连接、.21*cnjy*com
(1)求证:为的中点.
(2)若的半径为,的度数为,求线段的长.
【答案】(1)证明见详解;(2).
【解析】
【分析】
(1)通过同弧或等弧所对的圆周角相等,结合、互相垂直,证明,可得结果;
(2)连接AC,OA,OB,AB,证明M为AE中点,得MN为的中位线,结合的度数为90°,半径为8,得到AB的长度,进而得到MN长度.
【详解】
(1)∵点为的中点
∴
∴
∵
∴
∴
∵
∴°
在和中
∴
∴
∴点N为BE中点
(2)连接CA,AB,OA,OB,如图所示:
∵点为的中点
∴
在和中
∴
∴,即M为AE中点
∵N为BE中点
∴MN为的中位线
又∵的半径为,的度数为
∴,OA=OB=8
∴
∴
【点睛】本题_è?????????????¨???_周角定理的性质结合全等三角形证明中点问题,同时考查了直角三角形的边长的计算,及中位线的作用,熟知以上知识是解题的关键.
8.(2019·湖北省直辖县级单位·中考真题)已知ABC内接于,的平分线交于点D,连接DB,DC.
(1)如图①,当时,请直接写出线段AB,AC,AD之间满足的等量关系式: ;
(2)如图②,当时,试探究线段AB,AC,AD之间满足的等量关系,并证明你的结论;
(3)如图③,若BC=5,BD=4,求 的值.
【答案】(1)AB+AC=AD;(2);(3)
【解析】
【分析】
(1)在AD上截取AE=AB,_è?????BE?????±_条件可知△ABE和△BCD都是等边三角形,可证明△BED≌△BAC,可得DE=AC,则AB+AC=AD;
(2)延长AB至点M,使BM=AC,连接DM,证明△MBD≌△ACD,可得MD=AD,证得AB+AC=;
(3)延长AB至点N,使BN=AC,连接DN,证明△NBD≌△ACD,可得ND=AD,∠N=∠CAD,证△NAD∽△CBD,可得,
可由AN=AB+AC,求出的值.
【详解】
解:(1)如图①在AD上截取AE=AB,连接BE,
∵∠BAC=120°,∠BAC的平分线交⊙O于点D,
∴∠DBC=∠DAC=60°,∠DCB=∠BAD=60°,
∴△ABE和△BCD都是等边三角形,
∴∠DBE=∠ABC,AB=BE,BC=BD,
∴△BED≌△BAC(SAS),
∴DE=AC,
∴AD=AE+DE=AB+AC;
故答案为:AB+AC=AD.
(2)AB+AC=.理由如下:
如图②,延长AB至点M,使BM=AC,连接DM,
∵四边形ABDC内接于⊙O,
∴∠MBD=∠ACD,
∵∠BAD=∠CAD=45°,
∴BD=CD,
∴△MBD≌△ACD(SAS),
∴MD=AD,∠M=∠CAD=45°,
∴MD⊥AD.
∴AM=,即AB+BM=,
∴AB+AC=;
(3)如图③,延长AB至点N,使BN=AC,连接DN,
∵四边形ABDC内接于⊙O,
∴∠NBD=∠ACD,
∵∠BAD=∠CAD,
∴BD=CD,
∴△NBD≌△ACD(SAS),
∴ND=AD,∠N=∠CAD,
∴∠N=∠NAD=∠DBC=∠DCB,
∴△NAD∽△CBD,
∴,
∴,
又AN=AB+BN=AB+AC,BC=5,BD=4,
∴.
【点睛】本题属_???????????????é??_,考查了圆周角定理,全等三角形的判定与性质,相似三角形的判定和性质,等边三角形的判定与性质等知识,解题的关键是正确作出辅助线解决问题.
9.(2020·山东德州·中考真题)如图1,在平面直角坐标系中,点A的坐标是,在x轴上任取一点M.连接AM,分别以点A和点M为圆心,大于的长为半径作弧,两弧相交于G,H两点,作直线GH,过点M作x轴的垂线l交直线GH于点P.根据以上操作,完成下列问题.
探究:
(1)线段PA与PM的数量关系为________,其理由为:________________.
(2)在x轴上多次改变点M的位置,按上述作图方法得到相应点P的坐标,并完成下列表格:
M的坐标 …
…
P的坐标 …
…
猜想:
(3)请根据上述表格中P点的坐标,把这些点用平滑的曲线在图2中连接起来;观察画出的曲线L,猜想曲线L的形状是________.
验证:
(4)设点P的坐标是,根据图1中线段PA与PM的关系,求出y关于x的函数解析式.
应用:
(5)如图3,点,,点D为曲线L上任意一点,且,求点D的纵坐标的取值范围.
【答案】(1),线段垂直平分线上的点与这条线段两个端点的距离相等;(2)图见解析,抛物线;(3)见解析;(4);(5)
【解析】
【分析】
(1)由尺规作图的步骤可知,HG是AM的中垂线,结合中垂线的性质,即可得到答案;
(2)根据第(1)的作图方法,得到相应点P的位置,即可求解;
(3)用平滑的曲线作出图象,即可;
(4)过点P作轴于点E,用含x,y的代数式表示,,,结合勾股定理,即可得到答案;
(5)连接,由题意得当时,在的外接圆上,弧所对的圆心角为60°,的外接圆圆心为坐标原点O,设,求出b的值,进而即可求解.
【详解】
解:(1) 线段垂直平分线上的点与这条线段两个端点的距离相等
(2)
M的坐标 …
…
P的坐标 …
…
(3)草图见图2:形状:抛物线
(4)如图1,过点P作轴于点E,
,,
在中,
即
化简,得
∴y关于x的函数解析式为.
(5)连接,易得,又
∴为等边三角形,∴
当时,在的外接圆上,弧所对的圆心角为60°
其圆心在的垂直平分线y轴上,
∴的外接圆圆心为坐标原点O,
设,则,即 ①
又点D在该抛物线上
∴ ②
由①②联立解得:(舍去)
数形结合可得,
当时,点D的纵坐标的取值范围为
【点睛】本题主要考查尺规作作中垂线,二次函数的图象和性质,圆周角定理,解题关键是:熟练掌握垂直平分线的性质定理,构造三角形的外接圆.21教育名师原创作品
10.(202_0?·????±????è??_真题)如图,在△ABC中,∠ACB=90°,将△ABC沿直线AB翻折得到△ABD,连接CD交AB于点M.E是线段CM上的点,连接BE.F是△BDE的外接圆与AD的另一个交点,连接EF,BF,
(1)求证:△BEF是直角三角形;
(2)求证:△BEF∽△BCA;
(3)当AB=6,BC=m时,在线段CM正存在点E,使得EF和AB互相平分,求m的值.
【答案】(1)见解析;(2)见解析;(3)
【解析】
【分析】
(1)想办法证明∠BEF=90°即可解决问题(也可以利用圆内接四边形的性质直接证明).
(2)根据两角对应相等两三角形相似证明.
(3)证明四边形AFBE是平行四边形,推出FJ=BD=m,EF=m,由△ABC∽△CBM,可得BM=,由△BEF∽△BCA,推出,由此构建方程求解即可.
【详解】
(1)证明:由折叠可知,∠ADB=∠ACB=90°
∵∠EFB=∠EDB,∠EBF=∠EDF,
∴∠EFB+∠EBF=∠EDB+∠EDF=∠ADB=90°,
∴∠BEF=90°,
∴△BEF是直角三角形.
(2) 证明:∵BC=BD,
∴∠BDC=∠BCD,
∵∠EFB=∠EDB,
∴∠EFB=∠BCD,
∵AC=AD,BC=BD,
∴AB⊥CD,
∴∠AMC=90°,
∵∠BCD+∠ACD=∠ACD+∠CAB=90°,
∴∠BCD=∠CAB,
∴∠BFE=∠CAB,
∵∠ACB=∠FEB=90°,
∴△BEF∽△BCA.
(3) 设EF交AB于J.连接AE,如下图所示:
∵EF与AB互相平分,
∴四边形AFBE是平行四边形,
∴∠EFA=∠FEB=90°,即EF⊥AD,
∵BD⊥AD,
∴EF∥BD,
∵AJ=JB,
∴AF=DF,
∴ FJ=
∴ EF=
∵ △ABC∽△CBM
∴ BC:MB=AB:BC
∴ BM=,
∵ △BEJ∽△BME,
∴ BE:BM=BJ:BE
∴ BE=,
∵ △BEF∽△BCA,
∴
即
解得(负根舍去).
故答案为:
【点睛】本题_?±?????????????é??_,考查了圆周角定理,相似三角形的判定和性质平行四边形的判定和性质等知识,解题的关键是学会利用参数构建方程解决问题,属于中考压轴题.
_21?????????è?????(www.21cnjy.com)_
第24章 圆
24.1 圆的有关性质
1.圆
在一个平面内,一条线段OA绕它的一个端点O旋转一周,另一个端点A所形成的图形叫作______________.21教育网
圆心:固定的端点叫作圆心.
半径:线段OA的长度叫作这个圆的______________.
圆的表示方法:以点O为圆心的圆,记作“______________”,读作“圆O”.
同时从圆的定义中归纳:
(1)圆上各点到定点(圆心)的距离都等于定长(半径);
(2)到定点的距离等于定长的点都在同一个圆上.
圆的第二定义:所有到定点的距离等于定长的点组成的图形叫作圆.
2.垂直于弦的直径
(1)圆是轴对称图形,任何一条直径所在的直线都是它的________________,圆有_______________条对称轴.21·cn·jy·com
(2)垂直于弦的______________平分弦,并且平分弦所对的弧;平分弦(不是直径)的直径__________于弦,并且________________弦所对的弧.
3.弧、弦、圆心角
(1)顶点在圆心的角叫做_______________.
(2)在同圆或等圆中,相等的圆心角所对的弧________________,所对的弦也________________.
(3)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等.
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧也相等.
4.圆周角
(1)圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.
特征:①角的顶点在圆上;②角的两边都与圆相交.
(2)同弧所对的圆周角的度数没有变化,并且它的度数恰好等于这条弧所对的圆心角的度数的___________.
(3)在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的_______________.
(4)半圆(或直径)所对的圆周角是_____________,90°的圆周角所对的弦是_______________.
(5)如果一_????¤?è???????????_有顶点都在同一个圆上,这个多边形叫做_____________,这个圆叫做这个多边形的外接圆.圆内接四边形的______________.
1.圆 半径 ⊙O
2.(1)对称轴 无数 (2)直径 垂直 平分
3.(1)圆心角 (2)相等 相等
4.(2)一半 (3)一半 (4)直角 直径 (5)圆内接多边形 对角互补
帮—重点 垂径定理及其推论,圆周角定理及其推论
帮—难点 圆的有关概念、圆心角、圆周角的概念
帮—易错 弧、弦、圆心角的关系
一、圆的有关概念
圆中容易混淆的“两组基本概念”
1.弦与直径:(1)弦是连接圆上任意两点的线段,直径是经过圆心的弦.
(2)直径是弦,是圆中最长的弦,但弦不一定是直径.
2.弧与半圆:
(1)圆上任意两点分圆成两段弧,圆上任意一条直径的两个端点把圆分成两条孤,每一条弧叫作半圆.
(2)半圆是弧,但弧不一定是半圆.
下列说法:①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,但弧不一定是半圆.正确的说法有( )【来源:21·世纪·教育·网】
A.1个 B.2个 C.3个 D.4个
【答案】C
【解析】
【分析】
利用圆的有关定义及性质分别进行判断后即可确定正确的选项.
【详解】
①直径是弦,正确,符合题意;
②弦不一定是直径,错误,不符合题意;
③半径相等的两个半圆是等弧,正确,符合题意;
④能够完全重合的两条弧是等弧,原命题错误,不符合题意;
⑤半圆是弧,但弧不一定是半圆,正确,符合题意;
正确的有3个,
故选:C.
【点睛】本题考查了圆的认识及圆的有关定义,解题的关键是了解圆的有关概念,难度不大.
二、垂径定理及其推论的有关计算与证明
垂径定理应用中常作的辅助线:
(1)若已知圆心和弦,则连接圆心和弦的一个端点,即“连半径”,并作垂直于弦的直径,构造直角三角形;
(2)若已知圆心和弦(弧)的中点,则连接圆心和弦(弧)的中点,并延长使其与圆相交,得圆的直径,再“连半径”,构造直角三角形.
如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC、BC为直径作半圆,其中M,N分别是AC、BC为直径作半圆弧的中点,,的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )
A.17 B.18 C.19 D.20
【答案】C
【解析】
【分析】
连接OP,OQ,根据M,N分别是AC、BC为直径作半圆弧的中点,,的中点分别是P,Q.得到OP⊥AC,OQ⊥BC,从而得到H、I是AC、BC的中点,利用中位线定理得到OH+OI=(AC+BC)=13和PH+QI=6,从而利用AB=OP+OQ=OH+OI+PH+QI求解.
【详解】
连接OP,OQ,分别交AC,BC于H,I,
∵M,N分别是AC、BC为直径作半圆弧的中点,,的中点分别是P,Q,
∴OP⊥AC,OQ⊥BC,由对称性可知:H,P,M三点共线,I,Q,N三点共线,
∴H、I是AC、BC的中点,
∴OH+OI=(AC+BC)=13,
∵MH+NI=AC+BC=13,MP+NQ=7,
∴PH+QI=13﹣7=6,
∴AB=OP+OQ=OH+OI+PH+QI=13+6=19,
故选C.
【点睛】本题考查了中位线定理的应用,解题的关键是正确作出辅助线,题目中还考查了垂径定理和轴对称的知识,有难度.
三、应用垂径定理作图
圆弧中点的确定:由垂径定理可知垂直于弦的直径平分弦,并且平分弦所对的两条弧,所以常通过作孤所对的弦的垂直平分线确定孤的中点.
如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是
A.点Q B.点P
C.点R D.点M
【答案】A
【解析】连接BC,
作AB和BC的垂直平分线,它们相交于Q点.
故选A.
四、利用垂径定理解决实际问题
利用垂径定理解答弓形问题时,常通过作辅助线构造直角三角形,然后利用勾股定理求得相关线段的长,从而解决问题.【版权所有:21教育】
在直径为的圆柱形油槽内装入一些油后,截面如图,油面宽为,当油面宽为时,油上升了多少厘米?
王源的解题步骤如下:
[解]连接,过点作于点.
于点,且为弦,.
当时,在中,.
当时,在中,.
.即油上升了.
请问王源的解题过程正确吗?如果不正确,请写出正确的解题步骤.
【答案】王源的解题过程不正确.正确解题步骤见解析.油上升了或.
【解析】
【分析】
连接AO,过点O作OC⊥AB于点C,根据垂径定理结合勾股定理求出当AB=6cm和8cm时OC的长度,即可得出结论.
【详解】
王源的解题过程不正确.正确解题步骤如下:
连接,过点作于点,如图所示.
∵于点,且为弦,.
当时,在中,,;
当时,在中,.
或.
答:油上升了或.
【点睛】本题主要考查了垂径定理以及勾股定理,解题的关键是求出OC的长,根据OC的变化来得出结论.
五、利用圆周角定理及其推论求角的度数
计算圆心角和_?????¨è§?????????¨_意事项:
1.在进行有关圆心角与圆周角的计算时,应适当添加辅助线,以方便角度之间的转化.一条弧所对的圆心角只有一个,而所对的圆周角有无数个,它们都相等;
2.一条弦所对的圆心角只有一个,但它所对的圆周角却有无数个,在同一条弦的同侧的圆周角相等,在同一条弦的异侧的两个圆周角互补.
如图,在的外接圆上,所对的圆心角的度数比为.在上取一点,过分别作直线的平行线,交于两点,则的度数为( )
A.55° B.60° C.65° D.70°
【答案】C
【解析】
【分析】
根据题意即可求出所对的圆心角的度数,然后根据圆周角定理即可求出∠BAC的度数,再根据平行线的性质即可证出,最后根据三角形的内角和定理即可求出结论.
【详解】
解:所对的圆心角的度数比为
所对的圆心角的度数为
.
故选C.
【点睛】此题考查的是圆周角定理、平行线的性质和三角形的内角和定理,掌握圆周角定理、平行线的性质和三角形的内角和定理是解决此题的关键.
六、运用弧、弦、圆心角、圆周角的关系进行证明
圆中证明弧、弦、圆心角、圆周角相等或倍分关系的方法:
在圆中证明弧、弦、圆心角、圆周角_??????????????????_关系时,应从同类型元素(指弧、弦、角)的相等或倍分关系入手,转化为另一种元素的相等或倍分关系,从而得到问题的结论.
如图,以平行四边形的顶点为圆心,长为半径作,分别交于两点,交的延长线于点.
(1)求证:;
(2)连接,若,求的度数.
【答案】(1)详见解析;(2)70°
【解析】
【分析】
(1)通过平行四边形的对边平行,得到同位角和内错角相等,再利用等腰△ABE的两底角相等进行等量代换,进行求证;www-2-1-cnjy-com
(2)通过邻补角求得等腰△ABE的顶角∠BAE读数,再利用三角形内角和求底角∠B,平行四边形对角相等可求出∠D.
【详解】
(1)
证明:连接.
∵四边形是平行四边形,
,
,,
,
,
,
.
(2)解:为的直径,,
,
,
∵四边形是平行四边形,
.
【点睛】在圆的证明和计算中,证明两弧相等,常常需要构造弧所对的圆心角,通过证明圆心角相等来再进一步证明弧相等.
七、圆内接四边形
如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是
A.50° B.60°
C.80° D.100°
【答案】D
【解析】圆上取一点A,连接AB,AD,
∵点A、B,C,D在⊙O上,∠BCD=130°,∴∠BAD=50°,∴∠BOD=100°.
故选D.
八、圆中计算防漏解
已知圆的半径为13 cm,两弦AB∥CD,AB=24 cm,CD=10 cm,则两弦AB,CD间的距离是
A.7 cm B.17 cm
C.12 cm D.7 cm或17 cm
【易错提示】本题应分两种情况解答:(1)两弦在圆心的同侧;(2)两弦在圆心的异侧,易遗漏两弦在圆
心的异侧时的情况.
【正解】第一种情况:两弦在圆心的同侧时,如图,过点O作OE⊥弦CD,交CD于点E,交AB于点F.
∵AB∥CD,∴EF⊥AB,∴线段EF的长是AB,CD间的距离.
∵CD=10 cm,∴DE=5 cm.
∵OD=13 cm,∴由勾股定理可得OE=12 cm.
同理可求OF=5 cm,∴EF=OE?OF=7 cm.
第二种情况:两弦在圆心的异侧时,如图,过点O作OE⊥CD于点E,延长EO交AB于点F.
∵CD∥AB,∴EF⊥AB.∴线段EF的长是AB,CD间的距离,
∴EF=OE+OF=17 cm.故选D.
九、对圆心角与圆周角的性质理解不透彻
判断:(1)相等的圆心角所对的弧相等,所对的弦相等.( )
(2)相等的圆周角所对的弧相等.( )
【易错提示】误以为这两个题均是正确的.如图①,在同心圆中,∠AOB=∠COD,但即.
在图②中,与有公共点M,显然圆周角∠AMB=∠CMD,而.
【正解】(1)错误;(2)错误.
十、求圆周角时未分类讨论而漏解
如图,∠AOB=100°,点C在⊙O上,且点C不与A、B重合,则∠ACB的度数为
A.50° B.80°或50°
C.130° D.?50°或130°
【易错提示】点C可能在优弧上也可能在劣弧上,此题应分两种情况进行讨论.
【正解】①如图所示,当C点在优弧上时,因为∠AOB=100°,根据同弧所对圆周角是圆心角的一半,所以∠ACB=∠AOB=50°.
②如图所示,当C点在劣弧上时,
因为∠AOB=100°,所以优弧所对的圆心角为:360°?100°=260°,
根据同弧所对圆周角是圆心角的一半,所以∠ACB=130°.
综上所述,∠ACB的度数为50°或130°.
故选D.
一、单选题
1.已知点在线段上(点与点不重合),过点的圆记为圆,过点的圆记为圆,过点的圆记为圆,则下列说法中正确的是( )
A.圆可以经过点 B.点可以在圆的内部
C.点可以在圆的内部 D.点可以在圆内部
【答案】B
【解析】
【分析】
根据题意,画出符合题意的示意图,然后求解.
【详解】
解:∵点在线段上(点与点不重合),过点的圆记为圆,∴点可以在圆的内部,故A错误,B正确;∵过点的圆记为圆,∴点可以在圆的外部,故C错误;∵过点的圆记为圆,∴点可以在圆的外部,故D错误.
故选B.
【点睛】本题考查点与圆的位置关系,画出适当的辅助图形,采用数形结合的方法,更有助于解题.
2.如图,点A,B,C都在⊙O上,∠ABC=70°,则∠AOC的度数是( )
A.35° B.70° C.110° D.140°
【答案】D
【解析】
【分析】
根据圆周角定理问题可解.
【详解】
解:∵∠ABC所对的弧是,
∠AOC所对的弧是,
∴∠AOC=2∠ABC=2×70°=140°.
故选D.
【点睛】本题考查圆周角定理,解答关键是掌握圆周角和同弧所对的圆心角的数量关系.
3.如图,图中的弦共有( )
A.1条 B.2条 C.3条 D.4条
【答案】B
【解析】
【分析】
根据弦的定义解答即可.
【详解】
解:图形中有弦AB和弦CD,共2条,
故选B.
【点睛】本题考查弦的定义,熟记弦的定义是解题的关键.
4.下列说法错误的是( )
A.圆内接四边形的对角互补 B.圆内接四边形的邻角互补
C.圆内接平行四边形是矩形 D.圆内接梯形是等腰梯形
【答案】B
【解析】
【分析】
根据圆内接四边形的性质分别分析得出即可.
【详解】
解:A、圆内接四_è???????????è§????_补,正确,不合题意;
B、圆内接四边形的邻角互补,错误,符合题意;
C、圆内接平行四边形是矩形,正确,不合题意;
D、圆内接梯形是等腰梯形,正确,不合题意.
故选:B.21*cnjy*com
【点睛】此题主要考查了圆内接四边形的性质,正确把握圆内接四边形对角互补进而得出是解题关键.
二、填空题
5.如图,是⊙O的直径,交⊙O于点交⊙O于点,给出以下结论:①;②;③;④.其中正确结论的序号是_________.
【答案】①②③
【解析】
【分析】
①根据圆周角定理,同弧所对的圆周角等于其所对的圆心角的一半,②根据直径所对的圆周角是判断,③同一个圆中,圆周角相等,弧相等,④根据等腰直角三角形的判断方法判定.
【详解】
解:如图,连接.是的直径,.又,故②正确.是的平分线,.故③正确.是的直径,..是的直角边,是斜边,.故④错误.由圆周角定理知,,故①正确.
综上,正确的结论是①②③.
【点睛】本题考查直径所对的圆周角是、等腰三角形的性质、角平分线的性质、圆周角定理等,知识综合性较强,是常见考点,难度一般,熟练掌握相关知识是解题关键.
6.在同一个_??????,_??????_心角不超过180°时, 圆心角越大, 所对的弧______;所对的弦__________, 所对弦的弦心距____________.
【答案】越长 越长 越短
【解析】
【分析】
根据圆心角定理解答即可.
【详解】
在同一个圆中, 当圆心角不超过180°时, 圆心角越大, 所对的弧越长,所对的弦越长,所对弦的弦心距越短.
故答案为越长;越长;越短.
【点睛】本题考查了圆心角定理及其推理,解此题的关键在于熟练掌握其知识点.
7.如图,分别以四边形ABCD(边长均大于4)的四个顶点为圆心,2为半径画圆,则图中四个阴影部分的面积之和是________.
【答案】4π
【解析】
【分析】
根据平行四边形的内角和等于360°可知,图中阴影部分的面积正好等于一个圆的面积,然后根据圆的面积公式列式计算即可得解.
【详解】
解:∵平行四边形ABCD的边长均大于4,各弧的半径都是2,
∴图中阴影部分的面积等于一个圆的面积,
即π?22=4π.
故答案为4π.
【点睛】本题考查了平行四边形的内角和等于360°的性质,判断出阴影部分的面积等于一个圆的面积是解题的关键.
8.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积(弦×矢+矢2).孤田是由圆弧和其所对的弦围成(如图中的阴影部分),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,运用垂径定理(当半径⊥弦时,平分)可以求解.现已知弦米,半径等于5米的弧田,按照上述公式计算出弧田的面积为_____平方米.
【答案】10
【解析】
【分析】
根据垂径定理得到,由勾股定理得到,求得,根据弧田面积(弦×矢+矢2)即可得到结论.
【详解】
解:∵弦米,半径弦,
∴,
∴,
∴,
∴弧田面积(弦×矢+矢2),
故答案为10
【点睛】此题考查垂径定理的应用,关键是根据垂径定理和扇形面积解答.
三、解答题
9.如图,已知E是⊙O上任意一点,CD平分∠ACB,求证:ED平分∠AEB.
【答案】见解析.
【解析】
【分析】
根据CD平分∠ACB,判断出,再根据弧相等,判断出∠AED=∠BED即可.
【详解】
∵平分,
∴,
∴
∴ED平分∠AEB.
【点睛】本题考查了圆周角定理,根据同弧所对的圆周角相等解答.
10.如图,在⊙O中,AB.AC是弦,,求的关系.
【答案】
【解析】
【分析】
过A作⊙O的直径,交⊙O于D,分别在等腰△OAB、等腰△OAC中,根据三角形外角的性质即可求出答案.
【详解】
过A作⊙O的直径,交⊙O于D;
中,,则,
同理可得:,
∵,
∴.
【点睛】本题考查了等腰三角形的性质及三角形的外角性质,正确添加辅助线是解题的关键.
一、单选题
1.如图,在中,已知AB=CD,则AC与BD的关系是( )
A. B. C. D.不确定
【答案】A
【解析】
【分析】
根据已知条件可得,进而可得,根据圆心角、弧、弦的关系即可得
.
【详解】
,
,
,
故选:A.
【点睛】本题主要考查圆心角、弧、弦的关系,熟练掌握圆的性质是解题关键.
2.如图,在圆O中,弦AB=4,点C在AB上移动,连接OC,过点C作CD⊥OC交圆O于点D,则CD的最大值为 ( )
A. B.2 C. D.
【答案】B
【解析】
【分析】
连接OD,利用勾股定理得到CD,利用垂线段最短得到当OC⊥AB时,OC最小,根据垂径定理计算即可.
【详解】
连接OD,如图,设圆O的半径为r,
∵CD⊥OC,
∴∠DCO=90°,
∴CD=,
∴当OC的值最小时,CD的值最大,而OC⊥AB时,OC最小,
此时D、B重合,则由垂径定理可得:CD=CB=AC=AB=2,
∴CD的最大值为2.
故答案为:2.
【点睛】本题考查垂径定理和勾股定理,作辅助线构造直角三角形应用勾股定理,并熟记垂径定理内容是解题的关键.
3.如图,AB是⊙O的直径,BC是弦,点P是劣弧(含端点)上任意一点,若AB=5,BC=4,则AP的长不可能是( )
A.2 B.3 C.4 D.5
【答案】A
【解析】
【分析】
连接AC,如图,利用圆周角定理得到∠ACB=90°,利用勾股定理得到AC=3,则3≤AP≤5,然后对各选项进行判断.
【详解】
解:连接AC,如图,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴AC===3,
∵点P是劣弧(含端点)上任意一点,
∴AC≤AP≤AB,
即3≤AP≤5.
故选A.
【点睛】本题考查_????????¨è§???????_:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
二、填空题
4.如图,已知点经过原点,交轴正半轴于点.点在上,,圆心的坐标为__________.
【答案】
【解析】
【分析】
连接OP,OB,PB,延长BP交⊙P于E,连接OE,作EF⊥OA于F,BH⊥x轴于H.利用全等三角形的性质求出点E坐标即可解决问题.
【详解】
解:连接OP,OB,PB,延长BP交⊙P于E,连接OE,作EF⊥OA于F,BH⊥x轴于H.
∵∠BPO=2∠BAO,∠BAO=45°,
∴∠BPO=90°,
∵PO=OB,
∴△PBO是等腰直角三角形,
∵BE是直径,
∴∠BOE=90°,
∴∠OBE=∠OEB=45°,
∴OE=OB,
∵∠EOB=∠AOH=90°,
∴∠EOF=∠BOH,
∵∠EFO=∠BHO=90°,
∴△EFO≌△BHO(AAS),
∴OF=OH=5,EF=BH=2,
∴E(?2,5),
∵PE=PB,
∴P.
故答案为.
【点睛】本题考查圆周角定_????????¨??????è§?_形的判定和性质,等腰直角三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
5.如图,点A,B,D在⊙O上,∠A=25°,OD的延长线交直线BC于点C,且∠OCB=________,则直线BC与⊙O的位置关系为
【答案】40°
【解析】
【分析】
先根据直线BC与⊙O相切,得到∠OBC=90°,再利用同弧所对的圆周角与圆心角的关系求出∠BOC=2∠A=50°,可求出∠OCB=40°.
【详解】
∵直线BC与⊙O相切,
∴∠OBC=90°,
∵∠BOC=2∠A=50°,
∴∠OCB=40°,答案为:40°.
【点睛】本题考查了同弧所对的圆周角与圆心角的关系,及圆的切线的性质,关键是熟练掌握这些性质.
6.如图,半圆形纸片AMB_????????????1__cm,用如图所示的方法将纸片对折,使对折后半圆弧的中点M与圆心O重合,则折痕CD的长为________ .
【答案】cm
【解析】
【分析】
作MO交CD于E,则MO⊥CD.连接CO.根据勾股定理和垂径定理求解.
【详解】
作MO交CD于E,则MO⊥CD,连接CO,
对折后半圆弧的中点M与圆心O重合,
则ME=OE=OC,
在直角三角形COE中,CE=,
折痕CD的长为2×=(cm).
故答案为:cm
【点睛】作出辅助线,构造直角三角形,根据对称性,利用勾股定理解答.
三、解答题
7.如图,过的直径上两点,分别作弦,.
求证:(1);
(2).
【答案】(1)详见解析;(2)详见解析
【解析】
【分析】
(1)连接OC、OF,根据圆_???è§??????§??????_的关系即可得到结论;
(2)根据等腰三角形的性质得到∠A=∠OCA=∠BFC=∠B,等量代换得到∠BFC=∠ACF.根据平行线的性质得到∠AMC=∠ANE.根据全等三角形的性质即可得到结论.
【详解】
解:(1)如图,连接.
,
.
.
(2)
,
.
.
又.
.
在和中,
.
【点睛】本题考查了圆心角、弧、弦的关系,全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.【出处:21教育名师】
8.如图,已知为⊙O的直径且,点(不与重合)为⊙O上一个动点,线段经过点,且为⊙O上一点,的延长线与的延长线交于点.
(1)求证:;
(2)当点在⊙O上移动时,求四边形的最大面积.
【答案】(1)见解析;(2)8
【解析】
【分析】
(1)连接D_F???AF???é??_先证明四边形ADFE是矩形,推出EF=AD,即可解决问题.
(2)证明四边形EFCD是平行四边形,推出S矩形EFDA=S平行四边形EFCD,推出矩形EFDA的面积最大时,四边形EFCD的面积最大.
【详解】
(1)证明:连接DF,AF.
∵DE是直径,
∴∠EAD=90°,
∵FE⊥AB,
∴∠FEA=90°,
∴AF是直径,
∴∠ADF=90°,
∴∠FEA=∠EAD=∠ADF=90°,
∴四边形ADFE是矩形,
∴EF=AD,
∵EB=EA,∠BEF=∠EAD=90°,
∴△EFB≌△ADE(HL);
(2)解∵四边形ADFE是矩形,
∴EF∥AC,EF=AD,
∵BE=AE,
∴BF=CF,
∴AC=2EF,
∴EF=AD=CD,
∵EF∥CD,
∴四边形EFCD是平行四边形,
∵AD=CD,EF∥AC,
∴S矩形EFDA=S平行四边形EFCD,
∴矩形EFDA的面积最大时,四边形EFCD的面积最大,
当AF⊥DE时,矩形EFDA的面积最大,即矩形EFDA为正方形时,面积最大,
此时矩形EFDA的面积的最大值.
∴四边形FCDE的最大面积为8.
【点睛】本题考查了全等_???è§?????????¤???_和性质,圆周角定理,平行四边形的判定和性质,矩形的判定和性质,正方形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
9.说出下列点的轨迹是什么图形,并画出图形.
(1)在平面直角坐标系内,到x轴,y轴距离相等的点的轨迹.
(2)以已知点A为端点的线段AB=10cm,这线段的另一个端点的轨迹.
(3)已知直线上有两点A、B,且AB=3cm,与A、B构成面积为3cm2的三角形的点的轨迹.
【答案】(1)x轴、y轴所构成的四个角的平分线;(2)以点A为圆心,半径长为10cm的圆;(3)平行于直线且与直线的距离为的两条直线.
【解析】
【分析】
(1)根据角平分线的性质即可得答案;(2)根据圆的定义即可得答案;(3)根据等底等高的三角形面积相等,平行线间的距离相等的性质即可得答案.【来源:21cnj*y.co*m】
【详解】
(1)如图:∵角平分线上的点到角两边的距离相等,
∴在平面直角坐标系内,到x轴,y轴距离相等的点的轨迹是x轴、y轴所构成的四个角的平分线;
(2)如图,∵到定点的距离为定长的点的轨迹是以定点为圆心,定长为半径的圆,
∴点A为端点的线段AB=10cm,另一个端点B的轨迹为以点A为圆心,半径长为10cm的圆,
(3)如图,∵AB=3cm,与A、B构成面积为3cm2,
∴AB边的高为2cm,
∵等底等高的三角形面积相等,平行线间的距离相等,
∴另一个点的轨迹为平行于直线且与直线的距离为的两条直线.
【点睛】本题考查的是点的轨迹,熟练掌握角平分线的性质、圆的定义及平行线的性质是解题关键.
10.如图,B_C?????????O???_直径,点P是半圆弧的中点,点A是弧BP的中点,AD⊥BC于D,连结AB、PB、AC,BP分别与AD、AC相交于点E、F.
(1)求证:AE=BE;
(2)判断BE与EF是否相等吗,并说明理由;
(3)小李通过操作发现CF=2AB,请问小李的发现是否正确?若正确,请说明理由;若不正确,请写出CF与AB正确的关系式.
【答案】(1)见解析;(2)BE=EF,理由见解析;(3)小李的发现是正确的,理由见解析
【解析】
【分析】
(1)如图1,连_???AP?????±B_C是半⊙O的直径,AD⊥BC于D,得到∠ACB+∠ABC=∠BAD+∠ABD=90°,于是得到∠ACB=∠BAD,根据圆周角定理得到∠P=∠ACB=∠ABP,即可求出结论;
(2)根据圆周角定理求出∠ABE=∠BAE,求出AE=BE,求出∠CAD=∠AFB,求出AE=EF,即可得出答案;
(3)根据全等三角形的性质和判定求出BG=CF,AB=AG,即可得出答案.
【详解】
(1)如图1,连接AP,
∵BC是半⊙O的直径,
∴∠BAC=90°,
∵AD⊥BC于D,
∴∠ADB=90°,
∴∠ACB+∠ABC=∠BAD+∠ABD=90°,
∴∠ACB=∠BAD,
∵点A是弧BP的中点,
∴∠P=∠ACB=∠ABP,
∴∠ABE=∠BAE,
∴AE=BE;
(2)BE=EF,
理由是:∵BC是直径,AD⊥BC,
∴∠BAC=∠ADC=90°,
∴∠BAD=∠ACB,
∵A为弧BP中点,
∴∠ABP=∠ACB,
∴∠BAD=∠ABP,
∴BE=AE,∠FAD=∠AFB,
∴EF=AE,
∴BE=EF;
(3)小李的发现是正确的,
理由是:如图2,延长BA、CP,两线交于G,
∵P为半圆弧的中点,A是弧BP的中点,
∴∠PCF=∠GBP,∠CPF=∠BPG=90°,BP=PC,
在△PCF和△PBG中,
,
∴△PCF≌△PBG(ASA),
∴CF=BG,
∵BC为直径,
∴∠BAC=90°,
∵A为弧BP中点,
∴∠GCA=∠BCA,
在△BAC和△GAC中,
∴△BAC≌△GAC(ASA),
∴AG=AB=BG,
∴CF=2AB.
【点睛】本题考查_????????¨è§???????_,圆心角、弧、弦之间的关系,全等三角形的性质和判定等知识点的应用,主要考查学生综合运用性质进行推理和计算的能力,题目综合性比较强,有一定的难度.
一、单选题
1.(2020·浙_?±?????·??·???è??_真题)如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E.设∠AED=α,∠AOD=β,则( )
A.3α+β=180° B.2α+β=180° C.3α﹣β=90° D.2α﹣β=90°
【答案】D
【解析】
【分析】
根据直角三角形两锐角互余性质,用α表示∠CBD,进而由圆心角与圆周角关系,用α表示∠COD,最后由角的和差关系得结果.2-1-c-n-j-y
【详解】
解:∵OA⊥BC,
∴∠AOB=∠AOC=90°,
∴∠DBC=90°﹣∠BEO
=90°﹣∠AED
=90°﹣α,
∴∠COD=2∠DBC
=180°﹣2α,
∵∠AOD+∠COD=90°,
∴β+180°﹣2α=90°,
∴2α﹣β=90°,
故选:D.
【点睛】本题考查了圆周角定理以及直角三角形的两个锐角互余的关系,熟练掌握圆周角定理是解决本题的关键.
2.(2020·湖北武汉·中考真题)如图,在半径为3的⊙O中,是直径,是弦,是的中点,与交于点.若是的中点,则的长是( )
A. B. C. D.
【答案】D
【解析】
【分析】
连接DO、DA、DC,_è??DO???AC_交于点H,证明△DHE≌△BCE,得到DH=CB,同时OH是三角形ABC中位线,设OH=x,则BC=2x=DH,故半径DO=3x,解出x,最后在Rt△ACB中由勾股定理即可求解.
【详解】
解:连接DO、DA、DC、OC,设DO与AC交于点H,如下图所示,
∵D是的中点,∴DA=DC,∴D在线段AC的垂直平分线上,
∵OC=OA,∴O在线段AC的垂直平分线上,
∴DO⊥AC,∠DHC=90°,
∵AB是圆的直径,∴∠BCA=90°,
∵E是BD的中点,∴DE=BE,且∠DEH=∠BEC,
∴△DHE≌△BCE(AAS),
∴DH=BC,
又O是AB中点,H是AC中点,
∴HO是△ABC的中位线,
设OH=x,则BC=DH=2x,
∴OD=3x=3,∴x=1,
即BC=2x=2,
在Rt△ABC中,.
故选:D.
【点睛】本题考查了圆周角定理、三角形全等、勾股定理等,属于综合题,熟练掌握其性质和定理是解决此题的关键
3.(2020·浙江嘉兴·中考真题)如图,在等腰△ABC中,AB=AC=2,BC=8,按下列步骤作图:
①以点A为圆心,适当的长度为半径作弧,分别交AB,AC于点E,F,再分别以点E,F为圆心,大于EF的长为半径作弧相交于点H,作射线AH;
②分别以点A,B为圆心,大于AB的长为半径作弧相交于点M,N,作直线MN,交射线AH于点O;
③以点O为圆心,线段OA长为半径作圆.
则⊙O的半径为( )
A.2 B.10 C.4 D.5
【答案】D
【解析】
【分析】
如图,设OA交BC于T.解直角三角形求出AT,再在Rt△OCT中,利用勾股定理构建方程即可解决问题.21·世纪*教育网
【详解】
解:如图,设OA交BC于T.
∵AB=AC=2,AO平分∠BAC,
∴AO⊥BC,BT=TC=4,
∴AE=,
在Rt△OCT中,则有r2=(r﹣2)2+42,
解得r=5,
故选:D.
【点睛】本题考查作图——复杂作图,等腰三角形的性质,垂径定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.www.21-cn-jy.com
二、填空题
4.(2020·宁夏中考真题)我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”意思是:今有一圆柱形木材,埋在墙壁中,不知其大小.用锯去锯这木材,锯口深寸,锯道长尺(1尺寸).问这根圆形木材的直径是______寸.2·1·c·n·j·y
【答案】26
【解析】
【分析】
根据题意可得,由垂径定理可得尺寸,设半径,则,在中,根据勾股定理可得:,解方程可得出木材半径,即可得出木材直径.
【详解】
解:由题可知,
为半径,
尺寸,
设半径,
,
在中,根据勾股定理可得:
解得:,
木材直径为26寸;
故答案为:26.
【点睛】本题考查垂径定理结合_???è????????è?????_半径长度.如果题干中出现弦的垂线或者弦的中点,则可验证是否满足垂径定理;与圆有关的题目中如果求弦长或者求半径直径,也可以从题中寻找是否有垂径定理,然后构造直角三角形,用勾股定理求解.
5.(2018·海南中考真题_??????????????¨???_面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为_____.
【答案】(2,6)
【解析】
【分析】
此题涉及的知识点是平面直角坐标系_????????§è?¨??????_合应用.过点M作MF⊥CD于F,过C作CE⊥OA于E,在Rt△CMF中,根据勾股定理即可求得MF与EM,进而就可求得OE,CE的长,从而求得C的坐标.21cnjy.com
【详解】
∵四边形OCDB是平行四边形,点B的坐标为(16,0),
CD∥OA,CD=OB=16,
过点M作MF⊥CD于F,则
过C作CE⊥OA于E,
∵A(20,0),
∴OA=20,OM=10,
∴OE=OM?ME=OM?CF=10?8=2,
连接MC,
∴在Rt△CMF中,
∴点C的坐标为(2,6).
故答案为(2,6).
【点睛】此题重点考察学生对坐标与图形性质的实际应用,勾股定理,注意数形结合思想在解题的关键.
6.(2018·_é??é???±????????·_中考真题)如图,一下水管道横截面为圆形,直径为100cm,下雨前水面宽为60cm,一场大雨过后,水面宽为80cm,则水位上升______cm.21世纪教育网版权所有
【答案】10或70
【解析】
【分析】
分水位在圆心下以及圆心上两种情况,画出符合题意的图形进行求解即可得.
【详解】
如图,作半径于C,连接OB,
由垂径定理得:=AB=×60=30cm,
在中,,
当水位上升到圆心以下时??水面宽80cm时,
则,
水面上升的高度为:;
当水位上升到圆心以上时,水面上升的高度为:,
综上可得,水面上升的高度为30cm或70cm,
故答案为:10或70.
【点睛】本题考查了垂径定理的应用,掌握垂径定理、灵活运用分类讨论的思想是解题的关键.
三、解答题
7.(2020·江苏泰州·中考真题)如图,在中,点为的中点,弦、互相垂直,垂足为,分别与、相交于点、,连接、.21*cnjy*com
(1)求证:为的中点.
(2)若的半径为,的度数为,求线段的长.
【答案】(1)证明见详解;(2).
【解析】
【分析】
(1)通过同弧或等弧所对的圆周角相等,结合、互相垂直,证明,可得结果;
(2)连接AC,OA,OB,AB,证明M为AE中点,得MN为的中位线,结合的度数为90°,半径为8,得到AB的长度,进而得到MN长度.
【详解】
(1)∵点为的中点
∴
∴
∵
∴
∴
∵
∴°
在和中
∴
∴
∴点N为BE中点
(2)连接CA,AB,OA,OB,如图所示:
∵点为的中点
∴
在和中
∴
∴,即M为AE中点
∵N为BE中点
∴MN为的中位线
又∵的半径为,的度数为
∴,OA=OB=8
∴
∴
【点睛】本题_è?????????????¨???_周角定理的性质结合全等三角形证明中点问题,同时考查了直角三角形的边长的计算,及中位线的作用,熟知以上知识是解题的关键.
8.(2019·湖北省直辖县级单位·中考真题)已知ABC内接于,的平分线交于点D,连接DB,DC.
(1)如图①,当时,请直接写出线段AB,AC,AD之间满足的等量关系式: ;
(2)如图②,当时,试探究线段AB,AC,AD之间满足的等量关系,并证明你的结论;
(3)如图③,若BC=5,BD=4,求 的值.
【答案】(1)AB+AC=AD;(2);(3)
【解析】
【分析】
(1)在AD上截取AE=AB,_è?????BE?????±_条件可知△ABE和△BCD都是等边三角形,可证明△BED≌△BAC,可得DE=AC,则AB+AC=AD;
(2)延长AB至点M,使BM=AC,连接DM,证明△MBD≌△ACD,可得MD=AD,证得AB+AC=;
(3)延长AB至点N,使BN=AC,连接DN,证明△NBD≌△ACD,可得ND=AD,∠N=∠CAD,证△NAD∽△CBD,可得,
可由AN=AB+AC,求出的值.
【详解】
解:(1)如图①在AD上截取AE=AB,连接BE,
∵∠BAC=120°,∠BAC的平分线交⊙O于点D,
∴∠DBC=∠DAC=60°,∠DCB=∠BAD=60°,
∴△ABE和△BCD都是等边三角形,
∴∠DBE=∠ABC,AB=BE,BC=BD,
∴△BED≌△BAC(SAS),
∴DE=AC,
∴AD=AE+DE=AB+AC;
故答案为:AB+AC=AD.
(2)AB+AC=.理由如下:
如图②,延长AB至点M,使BM=AC,连接DM,
∵四边形ABDC内接于⊙O,
∴∠MBD=∠ACD,
∵∠BAD=∠CAD=45°,
∴BD=CD,
∴△MBD≌△ACD(SAS),
∴MD=AD,∠M=∠CAD=45°,
∴MD⊥AD.
∴AM=,即AB+BM=,
∴AB+AC=;
(3)如图③,延长AB至点N,使BN=AC,连接DN,
∵四边形ABDC内接于⊙O,
∴∠NBD=∠ACD,
∵∠BAD=∠CAD,
∴BD=CD,
∴△NBD≌△ACD(SAS),
∴ND=AD,∠N=∠CAD,
∴∠N=∠NAD=∠DBC=∠DCB,
∴△NAD∽△CBD,
∴,
∴,
又AN=AB+BN=AB+AC,BC=5,BD=4,
∴.
【点睛】本题属_???????????????é??_,考查了圆周角定理,全等三角形的判定与性质,相似三角形的判定和性质,等边三角形的判定与性质等知识,解题的关键是正确作出辅助线解决问题.
9.(2020·山东德州·中考真题)如图1,在平面直角坐标系中,点A的坐标是,在x轴上任取一点M.连接AM,分别以点A和点M为圆心,大于的长为半径作弧,两弧相交于G,H两点,作直线GH,过点M作x轴的垂线l交直线GH于点P.根据以上操作,完成下列问题.
探究:
(1)线段PA与PM的数量关系为________,其理由为:________________.
(2)在x轴上多次改变点M的位置,按上述作图方法得到相应点P的坐标,并完成下列表格:
M的坐标 …
…
P的坐标 …
…
猜想:
(3)请根据上述表格中P点的坐标,把这些点用平滑的曲线在图2中连接起来;观察画出的曲线L,猜想曲线L的形状是________.
验证:
(4)设点P的坐标是,根据图1中线段PA与PM的关系,求出y关于x的函数解析式.
应用:
(5)如图3,点,,点D为曲线L上任意一点,且,求点D的纵坐标的取值范围.
【答案】(1),线段垂直平分线上的点与这条线段两个端点的距离相等;(2)图见解析,抛物线;(3)见解析;(4);(5)
【解析】
【分析】
(1)由尺规作图的步骤可知,HG是AM的中垂线,结合中垂线的性质,即可得到答案;
(2)根据第(1)的作图方法,得到相应点P的位置,即可求解;
(3)用平滑的曲线作出图象,即可;
(4)过点P作轴于点E,用含x,y的代数式表示,,,结合勾股定理,即可得到答案;
(5)连接,由题意得当时,在的外接圆上,弧所对的圆心角为60°,的外接圆圆心为坐标原点O,设,求出b的值,进而即可求解.
【详解】
解:(1) 线段垂直平分线上的点与这条线段两个端点的距离相等
(2)
M的坐标 …
…
P的坐标 …
…
(3)草图见图2:形状:抛物线
(4)如图1,过点P作轴于点E,
,,
在中,
即
化简,得
∴y关于x的函数解析式为.
(5)连接,易得,又
∴为等边三角形,∴
当时,在的外接圆上,弧所对的圆心角为60°
其圆心在的垂直平分线y轴上,
∴的外接圆圆心为坐标原点O,
设,则,即 ①
又点D在该抛物线上
∴ ②
由①②联立解得:(舍去)
数形结合可得,
当时,点D的纵坐标的取值范围为
【点睛】本题主要考查尺规作作中垂线,二次函数的图象和性质,圆周角定理,解题关键是:熟练掌握垂直平分线的性质定理,构造三角形的外接圆.21教育名师原创作品
10.(202_0?·????±????è??_真题)如图,在△ABC中,∠ACB=90°,将△ABC沿直线AB翻折得到△ABD,连接CD交AB于点M.E是线段CM上的点,连接BE.F是△BDE的外接圆与AD的另一个交点,连接EF,BF,
(1)求证:△BEF是直角三角形;
(2)求证:△BEF∽△BCA;
(3)当AB=6,BC=m时,在线段CM正存在点E,使得EF和AB互相平分,求m的值.
【答案】(1)见解析;(2)见解析;(3)
【解析】
【分析】
(1)想办法证明∠BEF=90°即可解决问题(也可以利用圆内接四边形的性质直接证明).
(2)根据两角对应相等两三角形相似证明.
(3)证明四边形AFBE是平行四边形,推出FJ=BD=m,EF=m,由△ABC∽△CBM,可得BM=,由△BEF∽△BCA,推出,由此构建方程求解即可.
【详解】
(1)证明:由折叠可知,∠ADB=∠ACB=90°
∵∠EFB=∠EDB,∠EBF=∠EDF,
∴∠EFB+∠EBF=∠EDB+∠EDF=∠ADB=90°,
∴∠BEF=90°,
∴△BEF是直角三角形.
(2) 证明:∵BC=BD,
∴∠BDC=∠BCD,
∵∠EFB=∠EDB,
∴∠EFB=∠BCD,
∵AC=AD,BC=BD,
∴AB⊥CD,
∴∠AMC=90°,
∵∠BCD+∠ACD=∠ACD+∠CAB=90°,
∴∠BCD=∠CAB,
∴∠BFE=∠CAB,
∵∠ACB=∠FEB=90°,
∴△BEF∽△BCA.
(3) 设EF交AB于J.连接AE,如下图所示:
∵EF与AB互相平分,
∴四边形AFBE是平行四边形,
∴∠EFA=∠FEB=90°,即EF⊥AD,
∵BD⊥AD,
∴EF∥BD,
∵AJ=JB,
∴AF=DF,
∴ FJ=
∴ EF=
∵ △ABC∽△CBM
∴ BC:MB=AB:BC
∴ BM=,
∵ △BEJ∽△BME,
∴ BE:BM=BJ:BE
∴ BE=,
∵ △BEF∽△BCA,
∴
即
解得(负根舍去).
故答案为:
【点睛】本题_?±?????????????é??_,考查了圆周角定理,相似三角形的判定和性质平行四边形的判定和性质等知识,解题的关键是学会利用参数构建方程解决问题,属于中考压轴题.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
