专题24.3 正多边形和圆-2020-2021数学九上册同步课堂帮帮帮(含解析)
文档属性
| 名称 | 专题24.3 正多边形和圆-2020-2021数学九上册同步课堂帮帮帮(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-30 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第24章 圆
24.3 正多边形和圆
1.正多边形及有关概念
只要把一个圆分成 的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的
圆.
一个正多边形的外接圆的 叫_???è?????????¤?è??_形的中心,外接圆的 叫作这个正多边形的半径;正多边形每一边所对的 叫作正多边形的中心角;中心到正多边形的一边的距离叫做正多边形的 .
2.正多边形的有关计算
一般地,正n边形的一个内角的度数为 ,中心角的度数等于 ;正多边形的中心角与外角的大小 .
易错点:易把正多边形的内切圆的半径(即边心距)当作正多边形的半径.
1.相等 外接 圆心 半径 圆心角 边心距
2. 相等
帮—重点 正多边形及有关概念
帮—难点 正多边形及有关概念
帮—易错 混淆正多边形和圆的有关概念
一、圆内接正多边形的判断
证明一个圆内接多边形是正多边形的两种方法:
(1)证明圆内接多边形的每个内角相等,每条边也相等,二者缺一不可.
(2)证明圆内接多边形的各边所对的弧相等.
技巧:当边数是奇数时,各个内角相等的圆内接多边形是正多边形.
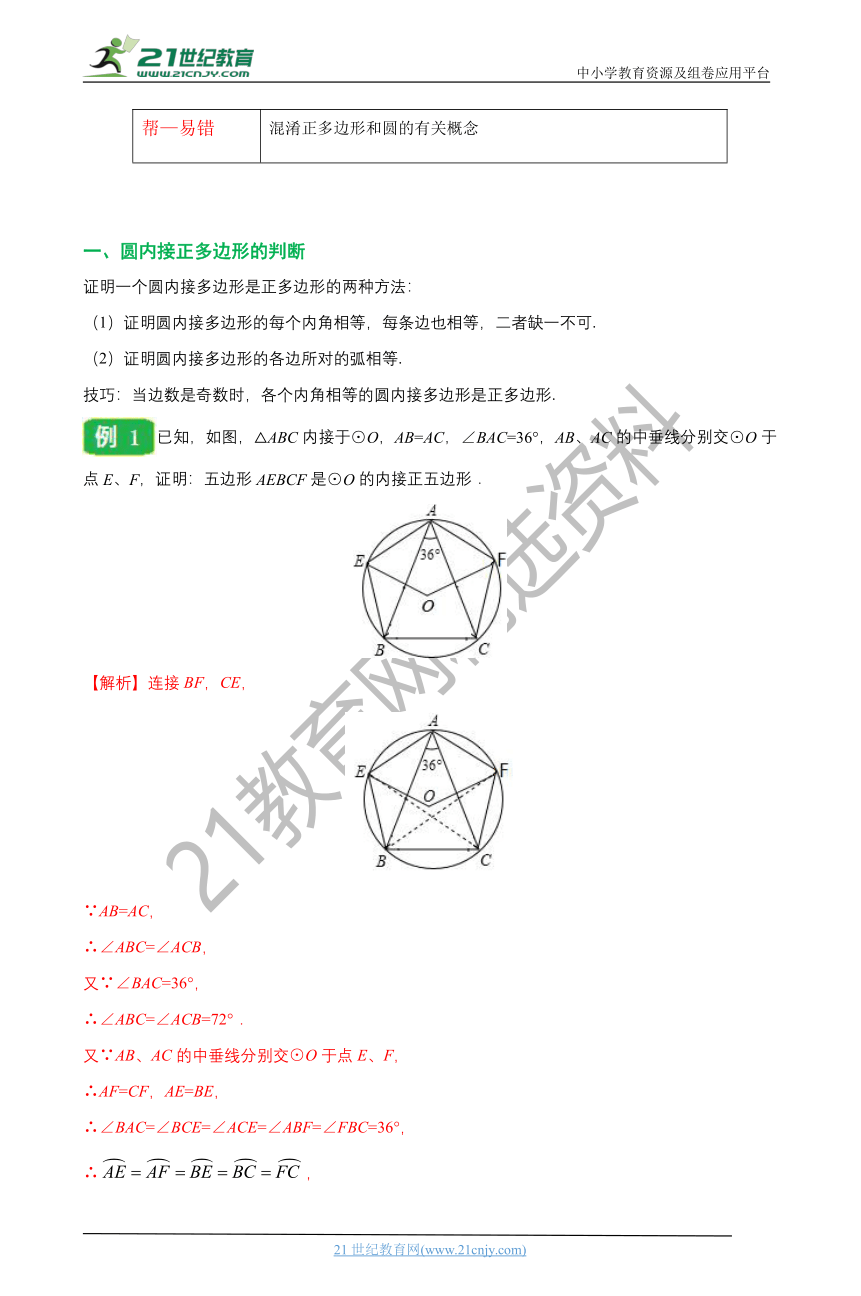
已知,如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,AB、AC的中垂线分别交⊙O于点E、F,证明:五边形AEBCF是⊙O的内接正五边形.
【解析】连接BF,CE,
∵AB=AC,
∴∠ABC=∠ACB,
又∵∠BAC=36°,
∴∠ABC=∠ACB=72°.
又∵AB、AC的中垂线分别交⊙O于点E、F,
∴AF=CF,AE=BE,
∴∠BAC=∠BCE=∠ACE=∠ABF=∠FBC=36°,
∴,
∴AE=AF=BE=BC=FC,
∴∠EAF=∠AFC=∠FCB=∠CBE=∠BEA.
∴五边形AEBCF为正五边形.
二、正多边形的有关计算
正多边形的相关计算技_?·§???
???1???_正n边形的半径、边心距、边的一半构成一个直角三角形.有关正n边形的计算问题都转化为直角三角形的问题,常作半径、边心距构造直角三角形;
(2)正六边形的边长等于它的半径,正三角形的边长等于它的半径的倍,正方形的边长等于它的半径的倍.
(2019·贵阳市)如图,正六边形ABCDEF内接于,连接BD.则∠CBD的度数是
A.30° B.45°
C.60° D.90°
【答案】A
【解析】∵在正六边形ABCDEF中,,
∴,故选A.
三、对正多边形的概念、性质理解模糊
判断题(正确的画“√”,错误的画“×”).
(1)各边相等的多边形是正多边形;( )
(2)圆内接菱形是正方形;( )
(3)各个角相等的圆内接多边形是正多边形;( )
(4)正多边形都是中心对称图形.( )
【易错提示】易因不理解正多边形的概念、性质而出错.
(1)菱形的各边相等,但它不一定是正方形;
(2)圆内接菱形的四个顶点将圆周4等分,所以它是正方形;
(3)圆内接矩形的各角都相等,但它不一定是正方形;
(4)当正多边形的边数为奇数时,该正多边形不是中心对称图形.
【正解】(1)×(2)√(3)×(4)×
四、混淆正多边形和圆的有关概念致错
求边长为a的正方形的半径.
【易错提示】正多边形有外接圆和内切圆,这两个圆是同心圆.正多边形的半径是指它的外接圆的半径,不要误认为正多边形的半径是它的内切圆半径
【正解】作正方形ABCD的外接圆,连接OA,OB.
在△AOB中,AB=a,∠AOB==90°,OA=OB.
由勾股定理,得OA2+OB2=a2,
∴,即边长为a的正方形的半径为.
一、单选题
1.如图,四边形ABCD内接于⊙O,F是上一点,且,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=110°,∠BAC=20°,则∠E的度数为( )
A.60° B.55° C.50° D.45°
【答案】C
【解析】
【分析】
先根据圆内接四边形的性质求出∠ADC的度数, 再由圆周角定理得出∠DCE的度数,根据三角形外角的性质即可得出结论.21·cn·jy·com
【详解】
解:四边形ABCD内接于⊙O,∠ABC=110°,
∠ADC=- ∠ABC=,
, ∠BAC=,
∠DCE=∠BAC=,
∠E=∠ADC - ∠DCE=70 - =.
故选C.
【点睛】本题主要考查圆内接四边形的性质及 圆心角、 弧、 弦的关系,需灵活运用各知识求解.
2.如图,已知△ABC为⊙O的内接三角形,AB>AC.E为的中点,过E作EF⊥AB于F.若AF=1,AC=4,∠C=60°,则⊙O的面积是( )
A.8π B.10π C.12π D.18π
【答案】C
【解析】
【分析】
在BF上截取_BM???AC???_连接BE,EM,AE,CE,证明△BEM≌△CEA(SAS),得出EM=AE,则AF=FM=1,求出AB=6,过点A作直径AN,连结BN,求出AN,则答案可求出.
【详解】
解:在BF上截取BM=AC,连接BE,EM,AE,CE,
∵E为的中点,
∴
∴BE=CE,
在△BEM和△CEA中,
,
∴△BEM≌△CEA(SAS),
∴EM=AE,
∵EF⊥AB,
∴AF=FM=1,
∴AB=AF+FM+BM=1+1+4=6,
过点A作直径AN,连结BN,
∵∠ACB=60°,
∴∠ANB=60°,
∴=sin60°,
∴AN==
∴OA=,
∴⊙O的面积是=12π.
故选:C.
【点睛】本题考查了三角形的外接圆_????¤?????????¨???_三角形的判定与性质,直角三角形的性质,垂径定理,等腰三角形的性质等知识,正确作出辅助线,构造全等三角形是解题的关键.
3.如图所示,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为( )
A.8 B.9 C.10 D.11
【答案】D
【解析】
∵⊙O内切于四边形ABCD,
∴AD+BC=AB+CD,
∵AB=10,BC=7,CD=8,
∴AD+7=10+8,
解得:AD=11.
故选D.
4.如图,把正六边形各边按同_????????????é?????_使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,…,重复上述过程,经过2020次后,所得到的正六边形的边长是原正六边形边长的( )21*cnjy*com
A.倍 B.倍 C.倍 D.倍
【答案】C
【解析】
【分析】
先根据正六边形的性质_?????????1??????_数,再根据AD=CD=BC判断出△ABC的形状及∠2的度数,求出AB的长,进而可得出,经过2020次后,即可得出所得到的正六边形的边长.
【详解】
∵此六边形是正六边形,
∴∠1=180°-120°=60°,
∵AD=CD=BC,
∴△BCD为等边三角形,
∴BD=AC,
∴△ABC是直角三角形
又∵BC=AC,
∴∠2=30°,
∴AB=BC=CD,
同理可得,经过2次后,所得到的正六边形是原正六边形边长的倍,
,
∴经过2020次后,所得到的正六边形的边长是原正六边形边长的倍.
【点睛】本题考查了正多边形和圆,正多边形内角的性质,直角三角形的判定,含30度角的直角三角形的性质等,能总结出规律是解此题的关键.
5.正五边形的画法通常是先把圆分成五等份,然后连接五等分点而得,这种画法的理论依据应( )
A.把圆等分,顺次连接各分点得到的多边形是圆的内接正边形
B.把圆等分,依次过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正边形
C.各边相等,并且各角也相等的多边形是正多边形
D.用量角器等分圆是一种简单而常用的方法
【答案】A
【解析】
【分析】
根据圆的内接正多边形的定义即可得答案.
【详解】
正五边形的画法通常是先把圆分成五等份,然后连接五等分点而得,这种画法的理论依据是把圆等分,顺次连接各分点得到的多边形是圆的内接正边形.
故选A.
【点睛】本题考查圆的内接正多边形的定义,把圆等分,顺次连接各分点得到的多边形是圆的内接正边形.
6.正五边形的中心角等于( )
A.18° B.36° C.54° D.72°
【答案】D
【解析】
【分析】
根据正n边形的圆中心角为计算即可.
【详解】
解:正五边形的中心角为.
故选D.
【点睛】本题考查正多边形的中心角,根据正多边形的圆心角定义可知:正n边形的圆中心角为.
7.若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r3,r4,r6,则r3:r4:r6等于( )
A. B. C. D.
【答案】A
【解析】
【分析】
经过圆心O作圆的内接正n边形的一边AB的垂线OC,垂足是C.连接OA,则在直角△OAC中,∠O=.OC是边心距,OA即半径.根据三角函数即可求解.
【详解】
解:设圆的半径为R,
则正三角形的边心距为R×cos60°.
四边形的边心距为R×cos45°,
正六边形的边心距为R×cos30°.
∴等于 .
故选A.
【点睛】此题主要考查了正_?¤?è??????????????_性质,解决本题的关键是构造直角三角形,得到用半径表示的边心距;注意:正多边形的计算一般要转化为解直角三角形的问题来解决.
二、填空题
8.如图,半径为1的⊙O与正五边形ABCDE的边AB、AE相切于点M、N,则劣弧弧MN的长度为__________.
【答案】
【解析】
试题分析:连接OM,ON,首先根据切线的性质和正五边形的性质求得圆心角的度数,然后利用弧长公式进行计算.
试题解析:如图:连接OM,ON,
∵⊙O与正五边形ABCDE的边AB、AE相切于点M、N,
∴OM⊥AB,ON⊥AC,
∵∠A=108°,
∴∠MON=72°,
∵半径为1,
∴劣弧的长度为:.
考点:正多边形和圆
三、解答题
9.如图所示,的底边BC的长为10cm,,,求它外接圆的直径.
【答案】
【解析】
【分析】
连接OA交BC于D,根据三线合一定理得出BD=DC,∠OAC=∠BAC,得出等边三角形OAC,推出∠AOC=60°,在△ODC中根据勾股定理求出即可半径,进而求得直径.
【详解】
解:如图所示,是的外接圆,连接OA交BC于D,
∵O是等腰三角形ABC的外心,AB=AC,
∴∠AOC=∠BOA,
∵OB=OC,
∴BD=DC,OA⊥BC,
∴由垂径定理得:BD=DC=5cm,
∠OAC=∠BAC=×120°=60°,
∵OA=OC,
∴△AOC是等边三角形,
∴∠AOC=60°,
∴∠DCO=90°-60°=30°
∴OC=2OD,
设OD=a,OC=2a,由勾股定理得:a2+52=(2a)2,
a=,
∴OC=2a=,
∴外接圆的直径=2OC=(cm).21·世纪*教育网
【点睛】本题考查等腰三角形_?????§è?¨??????è§?_形的外接圆和外心,勾股定理,等边三角形的性质和判定等知识点,此题有一定的难度,注意:此等腰三角形的外心在三角形外部.
10.如图所示,四边形ABCD内接于⊙O,延长AD,BC相交于点M,延长AB,DC相交于点N,∠M=40°,∠N=20°,求∠A的度数.
【答案】∠A=60°.
【解析】
【分析】
根据圆内接四边形的性质可得∠1=∠2=∠A,由圆周角定理可得答案.
【详解】
∵四边形ABCD内接于⊙O
∴∠1=∠2=∠A.
∵∠ADC+∠ABC=180°,∠ADC=∠M+∠2,∠ABC=∠1+∠N,
∴∠M+∠1+∠2+∠N=180°
∵∠M=40°,∠N=20°,∠1=∠2=∠A
∴∠A=60°.
【点睛】本题考查圆周角定理和圆内接四边形的性质,解题的关键是熟练掌握圆周角定理和圆内接四边形的性质.
一、单选题
1.如图,边长为_3?????????è?????_ABCDE,顶点A、B在半径为3的圆上,其他各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在圆上时,则点C转过的度数为( )
A.12° B.16° C.20° D.24°
【答案】A
【解析】
【分析】
根据点E旋转的角度和点C旋转的角度相等,所以求出点E旋转的角度即可.
【详解】
解: 如图
设圆心为O,连接OA, OB,点E落在圆上的点E'处.
AB=OA=OB,
∠OAB=,同理∠OAE'=,
∠EAB=,
∠EAO=∠EAB-∠OAB=,
∠EAE'=∠OAE'-∠EAO=-=
点E旋转的角度和点C旋转的角度相等,
点C旋转的角度为,
故选A.
【点睛】本题主要考查旋转的性质,注意与圆的性质的综合.
2.如图,正六边形的边长为_2???????????????_六边形的六条边为直径向外作半圆,与正六边形的外接圆围成的6个月牙形的面积之和(阴影部分面积)是( )www-2-1-cnjy-com
A. B. C. D.
【答案】A
【解析】
【分析】
图中阴影部分面积等于6个小半圆的面积和﹣(大圆的面积﹣正六边形的面积)即可得到结果.
【详解】
解:6个月牙形的面积之和,
故选A.
【点睛】本题考查了正多边形与圆,圆的面积的计算,正六边形的面积的计算,正确的识别图形是解题的关键.
3.边长为的正三角形的外接圆的半径为
A. B. C. D.
【答案】C
【解析】
【分析】
先根据题意画出图形,再根据正三角形的特点求出∠BOC的度数,由等腰三角形的性质及直角三角形的性质解答即可.【来源:21cnj*y.co*m】
【详解】
如图所示,连接OB,OC,过O作OD⊥BC;
∵BC=1,
∴BD=,
∵△ABC是正三角形,
∴∠BOC==120°,
∵OB=OC,
∴∠BOD==60°,
∴∠OBD=30°,OB=.
故选C.
【点睛】解决本题的关键是构造与外接圆半径相关的直角三角形.
4.如图,O是的外心,则
A. B. C. D.
【答案】C
【解析】
【分析】
根据等腰三角形的性质得到,根据三角形内角和定理计算即可.
【详解】
如图,
,
,
同理,,,
,
,
故选C.
【点睛】本题考查的是三角形的外接圆与外心,掌握三角形的外接圆的概念,三角形内角和定理是解题的关键.
二、填空题
5.如图,AB为半圆O的直径,C、D是半圆上的三等分点,若⊙O的半径为1,E为线段AB上任意一点,则图中阴影部分的面积为_____.【出处:21教育名师】
【答案】
【解析】
【分析】
根据同底同高的三角_???é???§??????????_可知点E无论在哪一点都与在点O时的面积相等,根据C、D是半圆上的三等分点,可知△OCD是等边三角形,即阴影部分的面积就是一个圆心角为60度的扇形的面积.
【详解】
连接CO,DO.
∵C、D是半圆上的三等分点,∴△OCD是等边三角形,∴阴影部分的面积=扇形COD的面积=.
【点睛】本题的关键是看出阴影部分的面积就是一个圆心角为60度的扇形的面积.
6.将一个边长为1的正八边形补成如图所示的正方形,这个正方形的边长等于________.(结果保留根号)
【答案】1+
【解析】
【分析】把正八边形的四条不相邻的_è?????é??????????°_的四边形就是满足条件的正方形,则三角形BDE是等腰直角三角形;正方形的边长等于正八边形的边长1加上DB的2倍,根据三角函数求得DE的长即可求解.
【详解】∵△BDE是等腰直角三角形,BE=1.
∴BD=BE?=.
∴正方形的边长等于AB+2BD=1+.
故答案为1+
【点睛】正确作出满足条件的正方形,理解所作正方形与已知正八边形之间的关系是解题的关键.
三、解答题
7.如图,AB是⊙O的直径,AC⊥AB,E为⊙O上的一点,AC=EC,延长CE交AB的延长线于点D.21教育网
(1)求证:CE为⊙O的切线;
(2)若OF⊥AE,OF=1,∠OAF=30°,求图中阴影部分的面积.(结果保留π)
【答案】(1)见解析;(2).
【解析】
【分析】
(1)首先连接_OE?????±AC_⊥AB,,可得∠CAD=90°,又由AC=EC,OA=OE,易证得∠CAE=∠CEA, ∠FAO=∠FEO,即可证得CD为⊙O的切线;
(2)根据题意可知∠OAF=30°,OF=1,可求得AE的长,又由S阴影= -,即可求得答案.
【详解】
(1)证明:连接OE
∵AC=EC,OA=OE
∴∠CAE=∠CEA, ∠FAO=∠FEO
∵AC⊥AB,
∴∠CAD=90°
∴∠CAE+∠EAO=90°
∴∠CEA+∠AEO=90°
即∠CEA=90°
∴OE⊥CD
∴CE为⊙O的切线
(2)解:
∵∠OAF=30°,OF=1
∴AO=2
∴AF= 即AE=
∴
∵∠AOE= 120°,AO=2
∴
∴S阴影=
【点睛】此题考查垂径定理及其推论,切线的判定与性质,扇形面积的计算,解题关键在于作辅助线.
8.如图,∠A=∠B=30°_???P???AB???_点,线段MV绕点P旋转,且M为射线AC上(不与点d重合)的任意一点,且N为射线BD上(不与点B重合)的一点,设∠BPN=α.
(1)求证:△APM≌△BPN;
(2)当MN=2BN时,求α的度数;
(3)若AB=4,60°≤α≤90°,直接写出△BPN的外心运动路线的长度。
【答案】(1)见解析;(2)30°;(3)
【解析】
【分析】
(1)由P为AB的中点,可得PA=PB,再由已知中∠A=∠B=30°,对顶角∠APM=∠BPN,根据ASA即可判定△APM≌△BPN;www.21-cn-jy.com
(2)由(1)中结论可知PM=PN,即MN=2PN,由已知MN=2BN,可得BN=PN,根据等边对等角,即α=∠B=30°;
(3)当α=60°时,由∠B=30°,可知MN⊥BD,此时BP的中点为△BPN的外心,当α=90°时,由∠B=30°,此时BN的中点为△BPN的外心,根据三角形中位线定理可得△BPN的外心运动路线的长度为PN的一半,即为.
【详解】
(1)证明:∵P是AB的中点,∴PA=PB , 在△APM和△BPN中,
∴△APM≌△BPN(ASA)
(2)解:由(1)得_??????APM???_△BPN , ∴PM=PN , ∴MN=2PN , ∵MN=2BN , ∴BN=PN , ∴α=∠B=30°
(3)解:
【点睛】本题考查三角形的外接圆与外心,解题关键在于熟练掌握全等三角形的判定与性质
9.如图,已知BD是四边形ABCD的一条对角线.请利用直尺和圆规在AB边上作一点P,使得∠BPC=∠BDC.(不写作法,保留作图痕迹)
【答案】见解析
【解析】
【分析】
作△BDC的外接圆,△DBC的外接圆与AB的交点P,即为所作的点P.
【详解】
(1)作△BDC的外接圆
(2)如图,△DBC的外接圆与AB的交点P,即为所作的点P.
【点睛】本题主要考查了复杂作图,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
10.如图,已知正五边形ABCDE,M是CD的中点,连接AC,BE,AM.
求证:(1)AC=BE;
(2)AM⊥CD.
【答案】见解析
【解析】
【分析】(1)先_è????????ABC_≌△EAB:AB=BC,AE=BA,∠ABC=∠EAB,所以全等,所以AC=BE;(2)连接AD,易证AC=AD(三角形ABC全等于三角形AED),所以三角形ACD为等腰三角形,又M为CD中点,所以AM垂直于CD
【详解】解:(1)由五边形ABCDE是正五边形,得AB=AE,∠ABC=∠BAE,AB=BC,
∴△ABC≌△EAB,∴AC=BE.
(2)连接AD,由五边形ABCDE是正五边形,得AB=AE,∠ABC=∠AED,BC=ED,
∴△ABC≌△AED,
∴AC=AD.
又∵M是CD的中点,
∴AM⊥CD.
【点睛】本题考核知识点:正多边形. 解题关键点:证三角形全等.
11.如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.21教育名师原创作品
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围.
【答案】(1)AB=AC(2)≤r<5
【解析】
【分析】
(1)连接,根据切线的性质和垂直得出,推出,求出,根据等腰三角形的判定推出即可;
(2)根据已知得出在的垂直平分线上,作出线段的垂直平分线,作,求出,求出范围,再根据相离得出,即可得出答案.21*cnjy*com
【详解】
(1)AB=AC,理由如下:
如图1,连结OB.
∵AB切⊙O于B,OA⊥AC,
∴∠OBA=∠OAC=90°,
∴∠OBP+∠ABP=90°,∠ACP+∠APC=90°,
∵OP=OB,
∴∠OBP=∠OPB,
∵∠OPB=∠APC,
∴∠ACP=∠ABC,
∴AB=AC;
(2)如图2,作出线段AC的垂直平分线MN,作OE⊥MN,则可以推出;
又∵圆O与直线MN有交点,
∴,
,
,
r2≥5,
∴,
又∵圆O与直线l相离,
∴r<5,
即.
图1 图2
【点睛】本题考查了等腰_???è§?????????§è?¨_和判定、直线与圆的位置关系等知识点的应用,主要培养学生运用性质进行推理和计算的能力.本题综合性比较强,有一定的难度.
一、单选题
1.(2020·辽宁营口·中考_???é??????????????_AB为⊙O的直径,点C,点D是⊙O上的两点,连接CA,CD,AD.若∠CAB=40°,则∠ADC的度数是( )
A.110° B.130° C.140° D.160°
【答案】B
【解析】
【分析】
连接BC,如图,利用圆周角定理得到∠ACB=90°,则∠B=50°,然后利用圆的内接四边形的性质求∠ADC的度数.
【详解】
解:如图,连接BC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠B=90°﹣∠CAB=90°﹣40°=50°,
∵∠B+∠ADC=180°,
∴∠ADC=180°﹣50°=130°.
故选:B.
【点睛】本题考查了圆_??¨è§????????????¨_同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
2.(2020·福建中考真题)如图,四边形内接于,,为中点,,则等于( )
A. B. C. D.
【答案】A
【解析】
【分析】
根据,为中点求出∠CBD=∠ADB=∠ABD,再根据圆内接四边形的性质得到∠ABC+∠ADC=180°,即可求出答案.
【详解】
∵为中点,
∴,
∴∠ADB=∠ABD,AB=AD,
∵,
∴∠CBD=∠ADB=∠ABD,
∵四边形内接于,
∴∠ABC+∠ADC=180°,
∴3∠ADB+60°=180°,
∴=40°,
故选:A.
【点睛】此题考查圆周角定理:在同圆中等弧所对的圆周角相等、相等的弦所对的圆周角相等,圆内接四边形的性质:对角互补.
3.(2019·富顺县_è?????????????????_考真题)如图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形翻折起来后,就能形成一个圆形桌面(可以近似看作正方形的外接圆),正方形桌面与翻折成圆形桌面的面积之比最接近( )
A. B. C. D.
【答案】C
【解析】
【分析】
连接AC,根据正方形的性质得到∠B=90°,根据圆周角定理得到AC为圆的直径,根据正方形面积公式、圆的面积公式计算即可.
【详解】
连接AC,
设正方形的边长为a,
∵四边形ABCD是正方形,
∴∠B=90°,
∴AC为圆的直径,
∴AC=AB=a,
则正方形桌面与翻折成的圆形桌面的面积之比为:,
故选C.
【点睛】本题考查的是正多边形和圆,掌握圆周角定理、正方形的性质是解题的关键.
二、填空题
4.(2020·黑龙江绥化·中考真题)如图,正五边形内接于,点P为上一点(点P与点D,点E不重合),连接、,,垂足为G,等于________度.
【答案】54
【解析】
【分析】
连接OC,OD,利用正五边形的性质求出∠COD的度数,再根据圆周角定理求得∠CPD,然后利用直角三角形的两锐角互余即可解答.【来源:21·世纪·教育·网】
【详解】
连接OC,OD,
∵ABCDE是正五边形,
∴∠COD=,
∴∠CPD=∠COD=36?,
∵,
∴∠DGP=90?
∴∠PDG=90?-∠CPD=90?-36?=54?,
故答案为:54?.
【点睛】本题主要考查了圆内接正多边形的性质、圆周角定理、直角三角形的性质,熟练掌握圆心角与圆周角之间的关系是解答的关键.2-1-c-n-j-y
5.(2018·四川宜宾·中考真_é?????????????????_国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积,设圆O的半径为1,若用圆O的外切正六边形的面积来近似估计圆O的面积,则S=_____.(结果保留根号)
【答案】
【解析】
分析:根据正多边形的定义可_?????????ABO_为等边三角形,根据等边三角形的性质结合OM的长度可求出AB的长度,再利用三角形的面积公式即可求出S的值.
详解:依照题意画出图象,如图所示.
∵六边形ABCDEF为正六边形,
∴△ABO为等边三角形,
∵⊙O的半径为1,
∴OM=1,
∴BM=AM=,
∴AB=,
∴S=6S△ABO=6×××1=2.
故答案为2.
点睛:本题考查了正多边形和圆、三角形的面积以及数学常识,根据等边三角形的性质求出正六边形的边长是解题的关键.
6.(201_7?·???è????????_·中考真题)如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是_____.
【答案】8+8
【解析】
解设直角三角形边是x,由勾股定理知22,解得x=,
所以周长等于8+8.
三、解答题
7.(2020·四川雅安·中考真题)如图,四边形内接于圆,,对角线平分.
(1)求证:是等边三角形;
(2)过点作交的延长线于点,若,求的面积.
【答案】(1)见解析;(2);
【解析】
【分析】
(1)根据三个内角相等的三角形是等边三角形即可判断;
(2)过点A作AE⊥CD,垂足为点E,过点B作BF⊥AC,垂足为点F.根据S四边形ABCD=S△ABC+S△ACD,分别求出△ABC,△ACD的面积,即可求得四边形ABCD的面积,然后通过证得△EAB≌△DCB(AAS),即可求得△BDE的面积=四边形ABCD的面积=.【版权所有:21教育】
【详解】
解:(1)证明:∵四边形ABCD内接于⊙O.
∴∠ABC+∠ADC=180°,
∵∠ABC=60°,
∴∠ADC=120°,
∵DB平分∠ADC,
∴∠ADB=∠CDB=60°,
∴∠ACB=∠ADB=60°,∠BAC=∠CDB=60°,
∴∠ABC=∠BCA=∠BAC,
∴△ABC是等边三角形;
(2)过点A作AM⊥CD,垂足为点M,过点B作BN⊥AC,垂足为点N.
∴∠AMD=90°
∵∠ADC=120°,
∴∠ADM=60°,
∴∠DAM=30°,
∴DM=AD=1,AM=,
∵CD=3,
∴CM=CD+DE=1+3=4,
∴S△ACD=CD-AM=×3×=,
在Rt△AMC中,∠AMD=90°,
∴AC=,
∵△ABC是等边三角形,
∴AB=BC=AC=,
∴BN=,
∴S△ABC=××=,
∴四边形ABCD的面积=+=,
∵BE∥CD,
∴∠E+∠ADC_=180?°???_
∵∠ADC=120°,
∴∠E=60°,
∴∠E=BDC,
∵四边形ABCD内接于⊙O,
∴∠EAB=∠BCD,
在△EAB和△DCB中,
,
∴△EAB≌△DCB(AAS),
∴△BDE的面积=四边形ABCD的面积=.
【点睛】本题考查圆内接四边_????????§è?¨??????_边三角形的判定和性质,勾股定理,三角形的面积等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
8.(2019·西藏中考真题)如图,在中.,以为直径的⊙分别交于点,点在的延长线上,且.
(1)求证:是⊙的切线;
(2)若,求点到的距离.
【答案】(1)见解析;(2)点到的距离为.
【解析】
【分析】
(1)连接,则,证明为等腰三角形,则,即,即可求解;
(2)在中,,,设点到的距离为,利用,即可求解.
【详解】
(1)连接,则,
为等腰三角形,
,
∴,即,
是⊙的切线;
(2)为等腰三角形,
,
∵,则,
在中,,,
设点到的距离为,
则,
即: ,
解得:,
故点到的距离为.
【点睛】本题考查的是切线定理的判断与运用,涉及到解直角三角形、三角形面积计算等,难度适中.
9.(2019·湖南张家界·中考真题)如图,AB为的直径,且,点C是上的一动点(不与A,B重合),过点B作的切线交AC的延长线于点D,点E是BD的中点,连接EC.
(1)求证:EC是的切线;
(2)当时,求阴影部分面积.
【答案】(1)证明见解析;(2)阴影部分面积为.
【解析】
【分析】
(1)如图,连接BC,OC,OE,证明,可得,进而根据BD是的切线,得到,继而得到,即可求得结论;
(2)先求出四边形OBEC的面积,继而根据阴影部分面积为进行求解即可得.
【详解】
(1)如图,连接BC,OC,OE,
AB为的直径,
,
在中,,
,
,,
,
,
BD是的切线,
,
,
OC为半径,
EC是的切线;
(2),,
,
,
,
,,
,
,
,
.
四边形OBEC的面积为,
阴影部分面积为.
【点睛】本题考查了切线的判定与性质,扇形的面积,熟练掌握相关知识是解题的关键.
10.(2019·山东威海·中考真题)(1)方法选择
如图①,四边形是的内接四边形,连接,,.求证:.
小颖认为可用截长法证明:在上截取,连接…
小军认为可用补短法证明:延长至点,使得…
请你选择一种方法证明.
(2)类比探究
(探究1)
如图②,四边形是的内接四边形,连接,,是的直径,.试用等式表示线段,,之间的数量关系,并证明你的结论.21cnjy.com
(探究2)
如图③,四边形是的内接四边形,连接,.若是的直径,,则线段,,之间的等量关系式是______.
(3)拓展猜想
如图④,四边形是的内接四边形,连接,.若是的直径,,则线段,,之间的等量关系式是______.
【答案】(1)方法选择:证明见解析;(2)【探究1】:;【探究2】;(3)拓展猜想:.
【解析】
【分析】
(1)方法选择:_?????????è?????è§?_形的性质得到∠ACB=∠ABC=60°,如图①,在BD上截取DM=AD,连接AM,由圆周角定理得到∠ADB=∠ACB=60°,得到AM=AD,根据全等三角形的性质得到BM=CD,于是得到结论;2·1·c·n·j·y
(2)类比探究:如图②,由BC是⊙O的直径,得到∠BAC=90°,根据等腰直角三角形的性质得到∠ABC=∠ACB=45°,过A作AM⊥AD交BD于M,推出△ADM是等腰直角三角形,求得DM=AD根据全等三角形的性质得到结论;
【探究2】
如图③,根据圆周角定理和三角形的内角和得到∠BAC=90°,∠ACB=60°,过A作AM⊥AD交BD于M,求得∠AMD=30°,根据直角三角形的性质得到MD=2AD,根据相似三角形的性质得到BM=CD,于是得到结论;
(3)如图④,由BC是⊙O的直径,得到∠BAC=90°,过A作AM⊥AD交BD于M,求得∠MAD=90°,根据相似三角形的性质得到BM=CD,DM=AD,于是得到结论.
【详解】
(1)方法选择:∵,
∴,
如图①,在上截取,连接,
∵,
∴是等边三角形,
∴,
∵,
∵,
∴,
∴,
∴;
(2)类比探究:如图②,
∵是的直径,
∴,
∵,
∴,
过作交于,
∵,
∴是等腰直角三角形,
∴,,
∴,
∴,
∵,
∴,
∴,
∴;
[探究2]如图③,∵若是的直径,,
∴,,
过作交于,
∵,
∴,
∴,
∵,,
∴,
∴,
∴,
∴;
故答案为;
(3)拓展猜想:;
理由:如图④,∵若是的直径,
∴,
过作交于,
∴,
∴,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
∴.
故答案为.
【点睛】本题考查了圆周角定理,圆内接四边形的性质,相似三角形的判定和性质,等腰直角三角形的性质,等边三角形的性质,正确的作出辅助线是解题的关键.21世纪教育网版权所有
_21?????????è?????(www.21cnjy.com)_
第24章 圆
24.3 正多边形和圆
1.正多边形及有关概念
只要把一个圆分成 的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的
圆.
一个正多边形的外接圆的 叫_???è?????????¤?è??_形的中心,外接圆的 叫作这个正多边形的半径;正多边形每一边所对的 叫作正多边形的中心角;中心到正多边形的一边的距离叫做正多边形的 .
2.正多边形的有关计算
一般地,正n边形的一个内角的度数为 ,中心角的度数等于 ;正多边形的中心角与外角的大小 .
易错点:易把正多边形的内切圆的半径(即边心距)当作正多边形的半径.
1.相等 外接 圆心 半径 圆心角 边心距
2. 相等
帮—重点 正多边形及有关概念
帮—难点 正多边形及有关概念
帮—易错 混淆正多边形和圆的有关概念
一、圆内接正多边形的判断
证明一个圆内接多边形是正多边形的两种方法:
(1)证明圆内接多边形的每个内角相等,每条边也相等,二者缺一不可.
(2)证明圆内接多边形的各边所对的弧相等.
技巧:当边数是奇数时,各个内角相等的圆内接多边形是正多边形.
已知,如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,AB、AC的中垂线分别交⊙O于点E、F,证明:五边形AEBCF是⊙O的内接正五边形.
【解析】连接BF,CE,
∵AB=AC,
∴∠ABC=∠ACB,
又∵∠BAC=36°,
∴∠ABC=∠ACB=72°.
又∵AB、AC的中垂线分别交⊙O于点E、F,
∴AF=CF,AE=BE,
∴∠BAC=∠BCE=∠ACE=∠ABF=∠FBC=36°,
∴,
∴AE=AF=BE=BC=FC,
∴∠EAF=∠AFC=∠FCB=∠CBE=∠BEA.
∴五边形AEBCF为正五边形.
二、正多边形的有关计算
正多边形的相关计算技_?·§???
???1???_正n边形的半径、边心距、边的一半构成一个直角三角形.有关正n边形的计算问题都转化为直角三角形的问题,常作半径、边心距构造直角三角形;
(2)正六边形的边长等于它的半径,正三角形的边长等于它的半径的倍,正方形的边长等于它的半径的倍.
(2019·贵阳市)如图,正六边形ABCDEF内接于,连接BD.则∠CBD的度数是
A.30° B.45°
C.60° D.90°
【答案】A
【解析】∵在正六边形ABCDEF中,,
∴,故选A.
三、对正多边形的概念、性质理解模糊
判断题(正确的画“√”,错误的画“×”).
(1)各边相等的多边形是正多边形;( )
(2)圆内接菱形是正方形;( )
(3)各个角相等的圆内接多边形是正多边形;( )
(4)正多边形都是中心对称图形.( )
【易错提示】易因不理解正多边形的概念、性质而出错.
(1)菱形的各边相等,但它不一定是正方形;
(2)圆内接菱形的四个顶点将圆周4等分,所以它是正方形;
(3)圆内接矩形的各角都相等,但它不一定是正方形;
(4)当正多边形的边数为奇数时,该正多边形不是中心对称图形.
【正解】(1)×(2)√(3)×(4)×
四、混淆正多边形和圆的有关概念致错
求边长为a的正方形的半径.
【易错提示】正多边形有外接圆和内切圆,这两个圆是同心圆.正多边形的半径是指它的外接圆的半径,不要误认为正多边形的半径是它的内切圆半径
【正解】作正方形ABCD的外接圆,连接OA,OB.
在△AOB中,AB=a,∠AOB==90°,OA=OB.
由勾股定理,得OA2+OB2=a2,
∴,即边长为a的正方形的半径为.
一、单选题
1.如图,四边形ABCD内接于⊙O,F是上一点,且,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=110°,∠BAC=20°,则∠E的度数为( )
A.60° B.55° C.50° D.45°
【答案】C
【解析】
【分析】
先根据圆内接四边形的性质求出∠ADC的度数, 再由圆周角定理得出∠DCE的度数,根据三角形外角的性质即可得出结论.21·cn·jy·com
【详解】
解:四边形ABCD内接于⊙O,∠ABC=110°,
∠ADC=- ∠ABC=,
, ∠BAC=,
∠DCE=∠BAC=,
∠E=∠ADC - ∠DCE=70 - =.
故选C.
【点睛】本题主要考查圆内接四边形的性质及 圆心角、 弧、 弦的关系,需灵活运用各知识求解.
2.如图,已知△ABC为⊙O的内接三角形,AB>AC.E为的中点,过E作EF⊥AB于F.若AF=1,AC=4,∠C=60°,则⊙O的面积是( )
A.8π B.10π C.12π D.18π
【答案】C
【解析】
【分析】
在BF上截取_BM???AC???_连接BE,EM,AE,CE,证明△BEM≌△CEA(SAS),得出EM=AE,则AF=FM=1,求出AB=6,过点A作直径AN,连结BN,求出AN,则答案可求出.
【详解】
解:在BF上截取BM=AC,连接BE,EM,AE,CE,
∵E为的中点,
∴
∴BE=CE,
在△BEM和△CEA中,
,
∴△BEM≌△CEA(SAS),
∴EM=AE,
∵EF⊥AB,
∴AF=FM=1,
∴AB=AF+FM+BM=1+1+4=6,
过点A作直径AN,连结BN,
∵∠ACB=60°,
∴∠ANB=60°,
∴=sin60°,
∴AN==
∴OA=,
∴⊙O的面积是=12π.
故选:C.
【点睛】本题考查了三角形的外接圆_????¤?????????¨???_三角形的判定与性质,直角三角形的性质,垂径定理,等腰三角形的性质等知识,正确作出辅助线,构造全等三角形是解题的关键.
3.如图所示,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为( )
A.8 B.9 C.10 D.11
【答案】D
【解析】
∵⊙O内切于四边形ABCD,
∴AD+BC=AB+CD,
∵AB=10,BC=7,CD=8,
∴AD+7=10+8,
解得:AD=11.
故选D.
4.如图,把正六边形各边按同_????????????é?????_使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,…,重复上述过程,经过2020次后,所得到的正六边形的边长是原正六边形边长的( )21*cnjy*com
A.倍 B.倍 C.倍 D.倍
【答案】C
【解析】
【分析】
先根据正六边形的性质_?????????1??????_数,再根据AD=CD=BC判断出△ABC的形状及∠2的度数,求出AB的长,进而可得出,经过2020次后,即可得出所得到的正六边形的边长.
【详解】
∵此六边形是正六边形,
∴∠1=180°-120°=60°,
∵AD=CD=BC,
∴△BCD为等边三角形,
∴BD=AC,
∴△ABC是直角三角形
又∵BC=AC,
∴∠2=30°,
∴AB=BC=CD,
同理可得,经过2次后,所得到的正六边形是原正六边形边长的倍,
,
∴经过2020次后,所得到的正六边形的边长是原正六边形边长的倍.
【点睛】本题考查了正多边形和圆,正多边形内角的性质,直角三角形的判定,含30度角的直角三角形的性质等,能总结出规律是解此题的关键.
5.正五边形的画法通常是先把圆分成五等份,然后连接五等分点而得,这种画法的理论依据应( )
A.把圆等分,顺次连接各分点得到的多边形是圆的内接正边形
B.把圆等分,依次过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正边形
C.各边相等,并且各角也相等的多边形是正多边形
D.用量角器等分圆是一种简单而常用的方法
【答案】A
【解析】
【分析】
根据圆的内接正多边形的定义即可得答案.
【详解】
正五边形的画法通常是先把圆分成五等份,然后连接五等分点而得,这种画法的理论依据是把圆等分,顺次连接各分点得到的多边形是圆的内接正边形.
故选A.
【点睛】本题考查圆的内接正多边形的定义,把圆等分,顺次连接各分点得到的多边形是圆的内接正边形.
6.正五边形的中心角等于( )
A.18° B.36° C.54° D.72°
【答案】D
【解析】
【分析】
根据正n边形的圆中心角为计算即可.
【详解】
解:正五边形的中心角为.
故选D.
【点睛】本题考查正多边形的中心角,根据正多边形的圆心角定义可知:正n边形的圆中心角为.
7.若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r3,r4,r6,则r3:r4:r6等于( )
A. B. C. D.
【答案】A
【解析】
【分析】
经过圆心O作圆的内接正n边形的一边AB的垂线OC,垂足是C.连接OA,则在直角△OAC中,∠O=.OC是边心距,OA即半径.根据三角函数即可求解.
【详解】
解:设圆的半径为R,
则正三角形的边心距为R×cos60°.
四边形的边心距为R×cos45°,
正六边形的边心距为R×cos30°.
∴等于 .
故选A.
【点睛】此题主要考查了正_?¤?è??????????????_性质,解决本题的关键是构造直角三角形,得到用半径表示的边心距;注意:正多边形的计算一般要转化为解直角三角形的问题来解决.
二、填空题
8.如图,半径为1的⊙O与正五边形ABCDE的边AB、AE相切于点M、N,则劣弧弧MN的长度为__________.
【答案】
【解析】
试题分析:连接OM,ON,首先根据切线的性质和正五边形的性质求得圆心角的度数,然后利用弧长公式进行计算.
试题解析:如图:连接OM,ON,
∵⊙O与正五边形ABCDE的边AB、AE相切于点M、N,
∴OM⊥AB,ON⊥AC,
∵∠A=108°,
∴∠MON=72°,
∵半径为1,
∴劣弧的长度为:.
考点:正多边形和圆
三、解答题
9.如图所示,的底边BC的长为10cm,,,求它外接圆的直径.
【答案】
【解析】
【分析】
连接OA交BC于D,根据三线合一定理得出BD=DC,∠OAC=∠BAC,得出等边三角形OAC,推出∠AOC=60°,在△ODC中根据勾股定理求出即可半径,进而求得直径.
【详解】
解:如图所示,是的外接圆,连接OA交BC于D,
∵O是等腰三角形ABC的外心,AB=AC,
∴∠AOC=∠BOA,
∵OB=OC,
∴BD=DC,OA⊥BC,
∴由垂径定理得:BD=DC=5cm,
∠OAC=∠BAC=×120°=60°,
∵OA=OC,
∴△AOC是等边三角形,
∴∠AOC=60°,
∴∠DCO=90°-60°=30°
∴OC=2OD,
设OD=a,OC=2a,由勾股定理得:a2+52=(2a)2,
a=,
∴OC=2a=,
∴外接圆的直径=2OC=(cm).21·世纪*教育网
【点睛】本题考查等腰三角形_?????§è?¨??????è§?_形的外接圆和外心,勾股定理,等边三角形的性质和判定等知识点,此题有一定的难度,注意:此等腰三角形的外心在三角形外部.
10.如图所示,四边形ABCD内接于⊙O,延长AD,BC相交于点M,延长AB,DC相交于点N,∠M=40°,∠N=20°,求∠A的度数.
【答案】∠A=60°.
【解析】
【分析】
根据圆内接四边形的性质可得∠1=∠2=∠A,由圆周角定理可得答案.
【详解】
∵四边形ABCD内接于⊙O
∴∠1=∠2=∠A.
∵∠ADC+∠ABC=180°,∠ADC=∠M+∠2,∠ABC=∠1+∠N,
∴∠M+∠1+∠2+∠N=180°
∵∠M=40°,∠N=20°,∠1=∠2=∠A
∴∠A=60°.
【点睛】本题考查圆周角定理和圆内接四边形的性质,解题的关键是熟练掌握圆周角定理和圆内接四边形的性质.
一、单选题
1.如图,边长为_3?????????è?????_ABCDE,顶点A、B在半径为3的圆上,其他各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在圆上时,则点C转过的度数为( )
A.12° B.16° C.20° D.24°
【答案】A
【解析】
【分析】
根据点E旋转的角度和点C旋转的角度相等,所以求出点E旋转的角度即可.
【详解】
解: 如图
设圆心为O,连接OA, OB,点E落在圆上的点E'处.
AB=OA=OB,
∠OAB=,同理∠OAE'=,
∠EAB=,
∠EAO=∠EAB-∠OAB=,
∠EAE'=∠OAE'-∠EAO=-=
点E旋转的角度和点C旋转的角度相等,
点C旋转的角度为,
故选A.
【点睛】本题主要考查旋转的性质,注意与圆的性质的综合.
2.如图,正六边形的边长为_2???????????????_六边形的六条边为直径向外作半圆,与正六边形的外接圆围成的6个月牙形的面积之和(阴影部分面积)是( )www-2-1-cnjy-com
A. B. C. D.
【答案】A
【解析】
【分析】
图中阴影部分面积等于6个小半圆的面积和﹣(大圆的面积﹣正六边形的面积)即可得到结果.
【详解】
解:6个月牙形的面积之和,
故选A.
【点睛】本题考查了正多边形与圆,圆的面积的计算,正六边形的面积的计算,正确的识别图形是解题的关键.
3.边长为的正三角形的外接圆的半径为
A. B. C. D.
【答案】C
【解析】
【分析】
先根据题意画出图形,再根据正三角形的特点求出∠BOC的度数,由等腰三角形的性质及直角三角形的性质解答即可.【来源:21cnj*y.co*m】
【详解】
如图所示,连接OB,OC,过O作OD⊥BC;
∵BC=1,
∴BD=,
∵△ABC是正三角形,
∴∠BOC==120°,
∵OB=OC,
∴∠BOD==60°,
∴∠OBD=30°,OB=.
故选C.
【点睛】解决本题的关键是构造与外接圆半径相关的直角三角形.
4.如图,O是的外心,则
A. B. C. D.
【答案】C
【解析】
【分析】
根据等腰三角形的性质得到,根据三角形内角和定理计算即可.
【详解】
如图,
,
,
同理,,,
,
,
故选C.
【点睛】本题考查的是三角形的外接圆与外心,掌握三角形的外接圆的概念,三角形内角和定理是解题的关键.
二、填空题
5.如图,AB为半圆O的直径,C、D是半圆上的三等分点,若⊙O的半径为1,E为线段AB上任意一点,则图中阴影部分的面积为_____.【出处:21教育名师】
【答案】
【解析】
【分析】
根据同底同高的三角_???é???§??????????_可知点E无论在哪一点都与在点O时的面积相等,根据C、D是半圆上的三等分点,可知△OCD是等边三角形,即阴影部分的面积就是一个圆心角为60度的扇形的面积.
【详解】
连接CO,DO.
∵C、D是半圆上的三等分点,∴△OCD是等边三角形,∴阴影部分的面积=扇形COD的面积=.
【点睛】本题的关键是看出阴影部分的面积就是一个圆心角为60度的扇形的面积.
6.将一个边长为1的正八边形补成如图所示的正方形,这个正方形的边长等于________.(结果保留根号)
【答案】1+
【解析】
【分析】把正八边形的四条不相邻的_è?????é??????????°_的四边形就是满足条件的正方形,则三角形BDE是等腰直角三角形;正方形的边长等于正八边形的边长1加上DB的2倍,根据三角函数求得DE的长即可求解.
【详解】∵△BDE是等腰直角三角形,BE=1.
∴BD=BE?=.
∴正方形的边长等于AB+2BD=1+.
故答案为1+
【点睛】正确作出满足条件的正方形,理解所作正方形与已知正八边形之间的关系是解题的关键.
三、解答题
7.如图,AB是⊙O的直径,AC⊥AB,E为⊙O上的一点,AC=EC,延长CE交AB的延长线于点D.21教育网
(1)求证:CE为⊙O的切线;
(2)若OF⊥AE,OF=1,∠OAF=30°,求图中阴影部分的面积.(结果保留π)
【答案】(1)见解析;(2).
【解析】
【分析】
(1)首先连接_OE?????±AC_⊥AB,,可得∠CAD=90°,又由AC=EC,OA=OE,易证得∠CAE=∠CEA, ∠FAO=∠FEO,即可证得CD为⊙O的切线;
(2)根据题意可知∠OAF=30°,OF=1,可求得AE的长,又由S阴影= -,即可求得答案.
【详解】
(1)证明:连接OE
∵AC=EC,OA=OE
∴∠CAE=∠CEA, ∠FAO=∠FEO
∵AC⊥AB,
∴∠CAD=90°
∴∠CAE+∠EAO=90°
∴∠CEA+∠AEO=90°
即∠CEA=90°
∴OE⊥CD
∴CE为⊙O的切线
(2)解:
∵∠OAF=30°,OF=1
∴AO=2
∴AF= 即AE=
∴
∵∠AOE= 120°,AO=2
∴
∴S阴影=
【点睛】此题考查垂径定理及其推论,切线的判定与性质,扇形面积的计算,解题关键在于作辅助线.
8.如图,∠A=∠B=30°_???P???AB???_点,线段MV绕点P旋转,且M为射线AC上(不与点d重合)的任意一点,且N为射线BD上(不与点B重合)的一点,设∠BPN=α.
(1)求证:△APM≌△BPN;
(2)当MN=2BN时,求α的度数;
(3)若AB=4,60°≤α≤90°,直接写出△BPN的外心运动路线的长度。
【答案】(1)见解析;(2)30°;(3)
【解析】
【分析】
(1)由P为AB的中点,可得PA=PB,再由已知中∠A=∠B=30°,对顶角∠APM=∠BPN,根据ASA即可判定△APM≌△BPN;www.21-cn-jy.com
(2)由(1)中结论可知PM=PN,即MN=2PN,由已知MN=2BN,可得BN=PN,根据等边对等角,即α=∠B=30°;
(3)当α=60°时,由∠B=30°,可知MN⊥BD,此时BP的中点为△BPN的外心,当α=90°时,由∠B=30°,此时BN的中点为△BPN的外心,根据三角形中位线定理可得△BPN的外心运动路线的长度为PN的一半,即为.
【详解】
(1)证明:∵P是AB的中点,∴PA=PB , 在△APM和△BPN中,
∴△APM≌△BPN(ASA)
(2)解:由(1)得_??????APM???_△BPN , ∴PM=PN , ∴MN=2PN , ∵MN=2BN , ∴BN=PN , ∴α=∠B=30°
(3)解:
【点睛】本题考查三角形的外接圆与外心,解题关键在于熟练掌握全等三角形的判定与性质
9.如图,已知BD是四边形ABCD的一条对角线.请利用直尺和圆规在AB边上作一点P,使得∠BPC=∠BDC.(不写作法,保留作图痕迹)
【答案】见解析
【解析】
【分析】
作△BDC的外接圆,△DBC的外接圆与AB的交点P,即为所作的点P.
【详解】
(1)作△BDC的外接圆
(2)如图,△DBC的外接圆与AB的交点P,即为所作的点P.
【点睛】本题主要考查了复杂作图,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
10.如图,已知正五边形ABCDE,M是CD的中点,连接AC,BE,AM.
求证:(1)AC=BE;
(2)AM⊥CD.
【答案】见解析
【解析】
【分析】(1)先_è????????ABC_≌△EAB:AB=BC,AE=BA,∠ABC=∠EAB,所以全等,所以AC=BE;(2)连接AD,易证AC=AD(三角形ABC全等于三角形AED),所以三角形ACD为等腰三角形,又M为CD中点,所以AM垂直于CD
【详解】解:(1)由五边形ABCDE是正五边形,得AB=AE,∠ABC=∠BAE,AB=BC,
∴△ABC≌△EAB,∴AC=BE.
(2)连接AD,由五边形ABCDE是正五边形,得AB=AE,∠ABC=∠AED,BC=ED,
∴△ABC≌△AED,
∴AC=AD.
又∵M是CD的中点,
∴AM⊥CD.
【点睛】本题考核知识点:正多边形. 解题关键点:证三角形全等.
11.如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.21教育名师原创作品
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围.
【答案】(1)AB=AC(2)≤r<5
【解析】
【分析】
(1)连接,根据切线的性质和垂直得出,推出,求出,根据等腰三角形的判定推出即可;
(2)根据已知得出在的垂直平分线上,作出线段的垂直平分线,作,求出,求出范围,再根据相离得出,即可得出答案.21*cnjy*com
【详解】
(1)AB=AC,理由如下:
如图1,连结OB.
∵AB切⊙O于B,OA⊥AC,
∴∠OBA=∠OAC=90°,
∴∠OBP+∠ABP=90°,∠ACP+∠APC=90°,
∵OP=OB,
∴∠OBP=∠OPB,
∵∠OPB=∠APC,
∴∠ACP=∠ABC,
∴AB=AC;
(2)如图2,作出线段AC的垂直平分线MN,作OE⊥MN,则可以推出;
又∵圆O与直线MN有交点,
∴,
,
,
r2≥5,
∴,
又∵圆O与直线l相离,
∴r<5,
即.
图1 图2
【点睛】本题考查了等腰_???è§?????????§è?¨_和判定、直线与圆的位置关系等知识点的应用,主要培养学生运用性质进行推理和计算的能力.本题综合性比较强,有一定的难度.
一、单选题
1.(2020·辽宁营口·中考_???é??????????????_AB为⊙O的直径,点C,点D是⊙O上的两点,连接CA,CD,AD.若∠CAB=40°,则∠ADC的度数是( )
A.110° B.130° C.140° D.160°
【答案】B
【解析】
【分析】
连接BC,如图,利用圆周角定理得到∠ACB=90°,则∠B=50°,然后利用圆的内接四边形的性质求∠ADC的度数.
【详解】
解:如图,连接BC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠B=90°﹣∠CAB=90°﹣40°=50°,
∵∠B+∠ADC=180°,
∴∠ADC=180°﹣50°=130°.
故选:B.
【点睛】本题考查了圆_??¨è§????????????¨_同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
2.(2020·福建中考真题)如图,四边形内接于,,为中点,,则等于( )
A. B. C. D.
【答案】A
【解析】
【分析】
根据,为中点求出∠CBD=∠ADB=∠ABD,再根据圆内接四边形的性质得到∠ABC+∠ADC=180°,即可求出答案.
【详解】
∵为中点,
∴,
∴∠ADB=∠ABD,AB=AD,
∵,
∴∠CBD=∠ADB=∠ABD,
∵四边形内接于,
∴∠ABC+∠ADC=180°,
∴3∠ADB+60°=180°,
∴=40°,
故选:A.
【点睛】此题考查圆周角定理:在同圆中等弧所对的圆周角相等、相等的弦所对的圆周角相等,圆内接四边形的性质:对角互补.
3.(2019·富顺县_è?????????????????_考真题)如图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形翻折起来后,就能形成一个圆形桌面(可以近似看作正方形的外接圆),正方形桌面与翻折成圆形桌面的面积之比最接近( )
A. B. C. D.
【答案】C
【解析】
【分析】
连接AC,根据正方形的性质得到∠B=90°,根据圆周角定理得到AC为圆的直径,根据正方形面积公式、圆的面积公式计算即可.
【详解】
连接AC,
设正方形的边长为a,
∵四边形ABCD是正方形,
∴∠B=90°,
∴AC为圆的直径,
∴AC=AB=a,
则正方形桌面与翻折成的圆形桌面的面积之比为:,
故选C.
【点睛】本题考查的是正多边形和圆,掌握圆周角定理、正方形的性质是解题的关键.
二、填空题
4.(2020·黑龙江绥化·中考真题)如图,正五边形内接于,点P为上一点(点P与点D,点E不重合),连接、,,垂足为G,等于________度.
【答案】54
【解析】
【分析】
连接OC,OD,利用正五边形的性质求出∠COD的度数,再根据圆周角定理求得∠CPD,然后利用直角三角形的两锐角互余即可解答.【来源:21·世纪·教育·网】
【详解】
连接OC,OD,
∵ABCDE是正五边形,
∴∠COD=,
∴∠CPD=∠COD=36?,
∵,
∴∠DGP=90?
∴∠PDG=90?-∠CPD=90?-36?=54?,
故答案为:54?.
【点睛】本题主要考查了圆内接正多边形的性质、圆周角定理、直角三角形的性质,熟练掌握圆心角与圆周角之间的关系是解答的关键.2-1-c-n-j-y
5.(2018·四川宜宾·中考真_é?????????????????_国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积,设圆O的半径为1,若用圆O的外切正六边形的面积来近似估计圆O的面积,则S=_____.(结果保留根号)
【答案】
【解析】
分析:根据正多边形的定义可_?????????ABO_为等边三角形,根据等边三角形的性质结合OM的长度可求出AB的长度,再利用三角形的面积公式即可求出S的值.
详解:依照题意画出图象,如图所示.
∵六边形ABCDEF为正六边形,
∴△ABO为等边三角形,
∵⊙O的半径为1,
∴OM=1,
∴BM=AM=,
∴AB=,
∴S=6S△ABO=6×××1=2.
故答案为2.
点睛:本题考查了正多边形和圆、三角形的面积以及数学常识,根据等边三角形的性质求出正六边形的边长是解题的关键.
6.(201_7?·???è????????_·中考真题)如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是_____.
【答案】8+8
【解析】
解设直角三角形边是x,由勾股定理知22,解得x=,
所以周长等于8+8.
三、解答题
7.(2020·四川雅安·中考真题)如图,四边形内接于圆,,对角线平分.
(1)求证:是等边三角形;
(2)过点作交的延长线于点,若,求的面积.
【答案】(1)见解析;(2);
【解析】
【分析】
(1)根据三个内角相等的三角形是等边三角形即可判断;
(2)过点A作AE⊥CD,垂足为点E,过点B作BF⊥AC,垂足为点F.根据S四边形ABCD=S△ABC+S△ACD,分别求出△ABC,△ACD的面积,即可求得四边形ABCD的面积,然后通过证得△EAB≌△DCB(AAS),即可求得△BDE的面积=四边形ABCD的面积=.【版权所有:21教育】
【详解】
解:(1)证明:∵四边形ABCD内接于⊙O.
∴∠ABC+∠ADC=180°,
∵∠ABC=60°,
∴∠ADC=120°,
∵DB平分∠ADC,
∴∠ADB=∠CDB=60°,
∴∠ACB=∠ADB=60°,∠BAC=∠CDB=60°,
∴∠ABC=∠BCA=∠BAC,
∴△ABC是等边三角形;
(2)过点A作AM⊥CD,垂足为点M,过点B作BN⊥AC,垂足为点N.
∴∠AMD=90°
∵∠ADC=120°,
∴∠ADM=60°,
∴∠DAM=30°,
∴DM=AD=1,AM=,
∵CD=3,
∴CM=CD+DE=1+3=4,
∴S△ACD=CD-AM=×3×=,
在Rt△AMC中,∠AMD=90°,
∴AC=,
∵△ABC是等边三角形,
∴AB=BC=AC=,
∴BN=,
∴S△ABC=××=,
∴四边形ABCD的面积=+=,
∵BE∥CD,
∴∠E+∠ADC_=180?°???_
∵∠ADC=120°,
∴∠E=60°,
∴∠E=BDC,
∵四边形ABCD内接于⊙O,
∴∠EAB=∠BCD,
在△EAB和△DCB中,
,
∴△EAB≌△DCB(AAS),
∴△BDE的面积=四边形ABCD的面积=.
【点睛】本题考查圆内接四边_????????§è?¨??????_边三角形的判定和性质,勾股定理,三角形的面积等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
8.(2019·西藏中考真题)如图,在中.,以为直径的⊙分别交于点,点在的延长线上,且.
(1)求证:是⊙的切线;
(2)若,求点到的距离.
【答案】(1)见解析;(2)点到的距离为.
【解析】
【分析】
(1)连接,则,证明为等腰三角形,则,即,即可求解;
(2)在中,,,设点到的距离为,利用,即可求解.
【详解】
(1)连接,则,
为等腰三角形,
,
∴,即,
是⊙的切线;
(2)为等腰三角形,
,
∵,则,
在中,,,
设点到的距离为,
则,
即: ,
解得:,
故点到的距离为.
【点睛】本题考查的是切线定理的判断与运用,涉及到解直角三角形、三角形面积计算等,难度适中.
9.(2019·湖南张家界·中考真题)如图,AB为的直径,且,点C是上的一动点(不与A,B重合),过点B作的切线交AC的延长线于点D,点E是BD的中点,连接EC.
(1)求证:EC是的切线;
(2)当时,求阴影部分面积.
【答案】(1)证明见解析;(2)阴影部分面积为.
【解析】
【分析】
(1)如图,连接BC,OC,OE,证明,可得,进而根据BD是的切线,得到,继而得到,即可求得结论;
(2)先求出四边形OBEC的面积,继而根据阴影部分面积为进行求解即可得.
【详解】
(1)如图,连接BC,OC,OE,
AB为的直径,
,
在中,,
,
,,
,
,
BD是的切线,
,
,
OC为半径,
EC是的切线;
(2),,
,
,
,
,,
,
,
,
.
四边形OBEC的面积为,
阴影部分面积为.
【点睛】本题考查了切线的判定与性质,扇形的面积,熟练掌握相关知识是解题的关键.
10.(2019·山东威海·中考真题)(1)方法选择
如图①,四边形是的内接四边形,连接,,.求证:.
小颖认为可用截长法证明:在上截取,连接…
小军认为可用补短法证明:延长至点,使得…
请你选择一种方法证明.
(2)类比探究
(探究1)
如图②,四边形是的内接四边形,连接,,是的直径,.试用等式表示线段,,之间的数量关系,并证明你的结论.21cnjy.com
(探究2)
如图③,四边形是的内接四边形,连接,.若是的直径,,则线段,,之间的等量关系式是______.
(3)拓展猜想
如图④,四边形是的内接四边形,连接,.若是的直径,,则线段,,之间的等量关系式是______.
【答案】(1)方法选择:证明见解析;(2)【探究1】:;【探究2】;(3)拓展猜想:.
【解析】
【分析】
(1)方法选择:_?????????è?????è§?_形的性质得到∠ACB=∠ABC=60°,如图①,在BD上截取DM=AD,连接AM,由圆周角定理得到∠ADB=∠ACB=60°,得到AM=AD,根据全等三角形的性质得到BM=CD,于是得到结论;2·1·c·n·j·y
(2)类比探究:如图②,由BC是⊙O的直径,得到∠BAC=90°,根据等腰直角三角形的性质得到∠ABC=∠ACB=45°,过A作AM⊥AD交BD于M,推出△ADM是等腰直角三角形,求得DM=AD根据全等三角形的性质得到结论;
【探究2】
如图③,根据圆周角定理和三角形的内角和得到∠BAC=90°,∠ACB=60°,过A作AM⊥AD交BD于M,求得∠AMD=30°,根据直角三角形的性质得到MD=2AD,根据相似三角形的性质得到BM=CD,于是得到结论;
(3)如图④,由BC是⊙O的直径,得到∠BAC=90°,过A作AM⊥AD交BD于M,求得∠MAD=90°,根据相似三角形的性质得到BM=CD,DM=AD,于是得到结论.
【详解】
(1)方法选择:∵,
∴,
如图①,在上截取,连接,
∵,
∴是等边三角形,
∴,
∵,
∵,
∴,
∴,
∴;
(2)类比探究:如图②,
∵是的直径,
∴,
∵,
∴,
过作交于,
∵,
∴是等腰直角三角形,
∴,,
∴,
∴,
∵,
∴,
∴,
∴;
[探究2]如图③,∵若是的直径,,
∴,,
过作交于,
∵,
∴,
∴,
∵,,
∴,
∴,
∴,
∴;
故答案为;
(3)拓展猜想:;
理由:如图④,∵若是的直径,
∴,
过作交于,
∴,
∴,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
∴.
故答案为.
【点睛】本题考查了圆周角定理,圆内接四边形的性质,相似三角形的判定和性质,等腰直角三角形的性质,等边三角形的性质,正确的作出辅助线是解题的关键.21世纪教育网版权所有
_21?????????è?????(www.21cnjy.com)_
同课章节目录
