人教版高中物理计算题强化专练-光学-普通用卷
文档属性
| 名称 | 人教版高中物理计算题强化专练-光学-普通用卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 172.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-29 00:00:00 | ||
图片预览

文档简介
计算题强化专练-光学
学校:___________姓名:___________班级:___________考号:___________
一、计算题
如图,某棱镜的横截面积为等腰直角三角形ABC,其折射率,一束单色光从AB面的O点入射,恰好在AC面上发生全反射,O、A的距离,求:
?
光在AB面的入射角的正弦值;
光从O点入射到AC面上发生全反射所经历的时间.
如图所示,光学玻璃制成的透明球体,半径为R.AB是竖直方向的直径.现有一束横截面为半径为R的细圆环的环形光束,沿AB方向射向球体,AB直径为光束的中心轴线.所有的光线经折射后恰好经过B点,从B点射出的光在水平光屏上形成一圆形亮环.水平光屏到B点的距离为L=R.求:
①球体材料的折射率;
②光屏上圆亮环的半径.
??
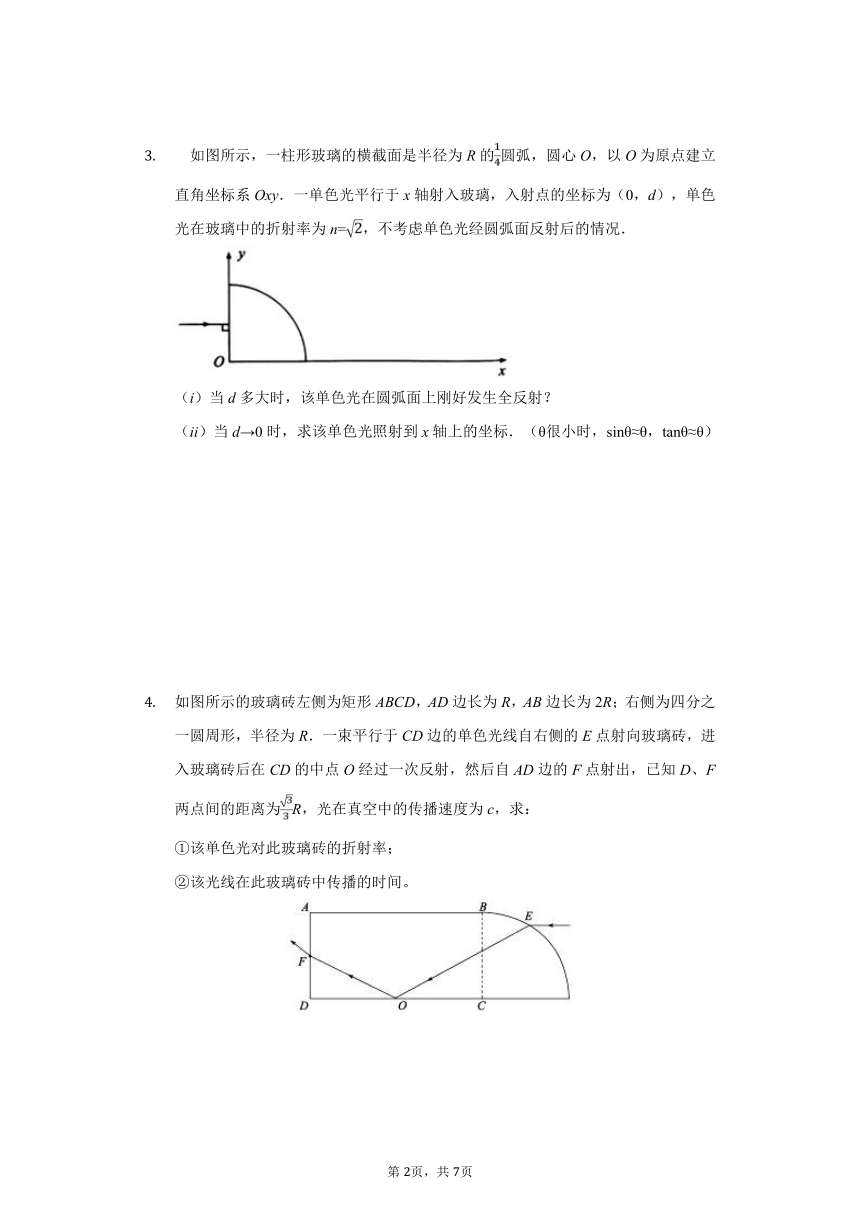
如图所示,一柱形玻璃的横截面是半径为R的圆弧,圆心O,以O为原点建立直角坐标系Oxy.一单色光平行于x轴射入玻璃,入射点的坐标为(0,d),单色光在玻璃中的折射率为n=,不考虑单色光经圆弧面反射后的情况.
(i)当d多大时,该单色光在圆弧面上刚好发生全反射?
(ii)当d→0时,求该单色光照射到x轴上的坐标.(θ很小时,sinθ≈θ,tanθ≈θ)
如图所示的玻璃砖左侧为矩形ABCD,AD边长为R,AB边长为2R;右侧为四分之一圆周形,半径为R.一束平行于CD边的单色光线自右侧的E点射向玻璃砖,进入玻璃砖后在CD的中点O经过一次反射,然后自AD边的F点射出,已知D、F两点间的距离为R,光在真空中的传播速度为c,求:
①该单色光对此玻璃砖的折射率;
②该光线在此玻璃砖中传播的时间。
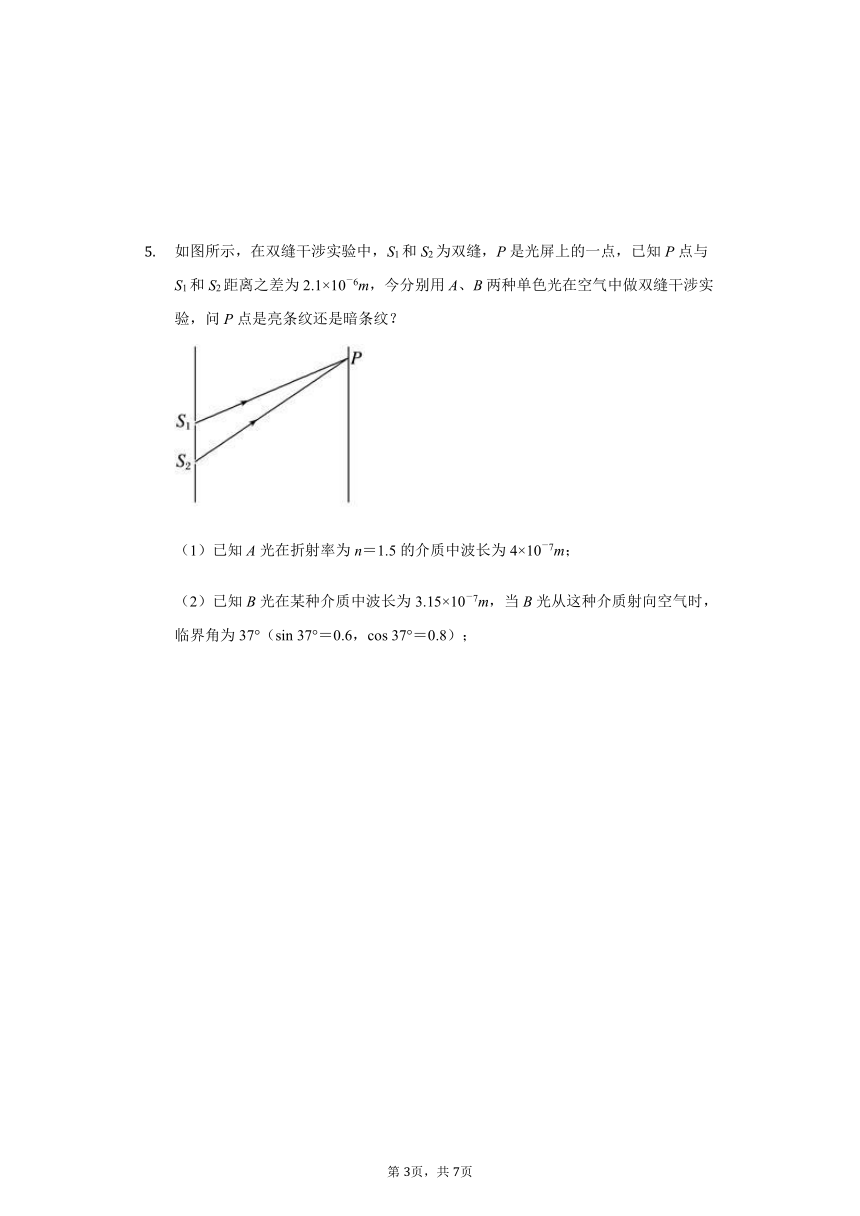
如图所示,在双缝干涉实验中,S1和S2为双缝,P是光屏上的一点,已知P点与S1和S2距离之差为2.1×10-6m,今分别用A、B两种单色光在空气中做双缝干涉实验,问P点是亮条纹还是暗条纹?
(1)已知A光在折射率为n=1.5的介质中波长为4×10-7m;
(2)已知B光在某种介质中波长为3.15×10-7m,当B光从这种介质射向空气时,临界角为37°(sin
37°=0.6,cos
37°=0.8);
答案和解析
1.【答案】解:①光路如图
根据全反射定律:sinC=?????????…①
解得????C=60°??????????…②
由几何关系得r=30°????…③
n=????????????…④
得?sini=??????????…⑤
②v==×108m/s???????…⑥
由几何关系得?x=????…⑦
而??t=?????…⑧
解得??t=2×10-9s?????…⑨
答:(1)光在AB面的入射角的正弦值为;
(2)光从O点入射到AC面上发生全反射所经历的时间为2×10-9s。
【解析】①单色光恰好在AC面上发生全反射,在AC面上的入射角恰好等于临界角C.先根据临界角公式sinC=,求得C,再由几何关系求得光线在AB面的折射角,即可由折射定律求解光在AB面的入射角的正弦值;
②光在棱镜中的传播速度由公式v=求解,进而得到经历时间。
对于几何光学问题,往往是折射定律、全反射临界角公式、光速公式和几何知识的综合应用,解答的基础是正确画出光路图,理清各个角度的关系,再进行研究。
2.【答案】解:①作出光路图如图所示,由几何关系知:
Rsinα=R,即:α=60°
由图知,α=2β,得β=30°
由折射定律有:n==
②由几何知识可得:光屏上圆亮环的半径为:
r=Ltanα=Rtan60°=R
答:①球体材料的折射率是;
②光屏上圆亮环的半径是R.
【解析】①作出光路图,由几何关系求出入射角和折射角,根据折射定律求解折射率.
②结合几何关系求出光屏上圆亮环的半径.
解决几何光学问题的关键画出光路图,结合折射定律和几何关系进行求解.
3.【答案】解:
?(i)如图答图1,当光射到圆弧面上的入射角等于临界角C时刚好发生全反射,则
??
sinθ==
解得
θ=45°
根据几何关系得d=Rsin45°=R
(ii)如图答2,当射到圆弧面上的入射角很小时,设折射角为α,入射角为β,由折射定律得:
??n=
在△OEF中,由正弦定理得=
当d→0时,sinθ≈θ,则得OF=R,α=nβ
联立解得OF=(2)R。
答:
(i)当d是R时,该单色光在圆弧面上刚好发生全反射;
(ii)当d→0时,该单色光照射到x轴上的坐标为(2)R。
【解析】?
?
本题的关键是作出光路图,运用几何知识辅助分析,结合折射定律和数学知识进行求解。
(i)当光射到圆弧面上时入射角等于临界角C时,恰好发生全反射.由sinC=求出临界角C,再由几何知识求d;
(ii)当d→0时,光射到圆弧面上的入射角很小,在圆弧面上发生折射,由折射定律列式,结合正弦定理求解即可。
4.【答案】解:①该单色光在玻璃砖中的光路如图所示,有:tanα==
解得:α=30°
由几何知识得在E点的入射角为:i1=60°,折射角为:i2=30°
得该单色光对此玻璃砖的折射率为:
n==
②由n=知该单色光在此玻璃砖中的传播速度为:v=
OF==
OE=2Rcos30°=R
该单色光在此玻璃砖中的路程为:x=OF+OE=R
该单色光在此玻璃砖中传播的时间为:t==
答:①该单色光对此玻璃砖的折射率是;
②该光线在此玻璃砖中传播的时间是。
【解析】①画出光路图,由几何关系求得入射角和折射角,根据折射定律可求得折射率;
②根据n=求得该单色光在此玻璃砖中的传播速度,再由几何关系求得光在玻璃中的传播距离,则传播时间可求解。
解决本题关键是作出光路图,再运用几何知识求解入射角折射角,要掌握几何光学常用的三个规律:折射定律n=、临界角公式sinC=和光速公式v=。
5.【答案】解:(1)设A光在空气中波长为λA,在介质中波长为λA',
由n===得,
?λA=nλA'=1.5×4×10-7m=6×10-7m.
根据光程差:δ=2.1×10-6m=(3+)λA,
知A光在P点是暗条纹
(2)设B光在空气中波长为λB,在介质中波长为λB',由n'=得,λB=n'λB',
又临界角C=37°所以n'=
所以λB==?m=5.25×10-7?m
根据光程差:δ=2.1×10-6?m=4λB知,B光在P点是亮条纹
【解析】解决本题的关键掌握形成明条纹或暗条纹的条件、折射率与波长的关系等等知识,基础题。
已知P点与S1和S2的距离之差,由出现亮暗的条件可判断是亮条纹或暗条纹.根据n=,v=λf,频率f相等,求出A光在空气中的波长;
对于B光,根据临界角公式sinC=求出折射率,再用同样的方法求出B光在空气中的波长.再判断是亮条纹还是暗条纹。
第2页,共2页
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、计算题
如图,某棱镜的横截面积为等腰直角三角形ABC,其折射率,一束单色光从AB面的O点入射,恰好在AC面上发生全反射,O、A的距离,求:
?
光在AB面的入射角的正弦值;
光从O点入射到AC面上发生全反射所经历的时间.
如图所示,光学玻璃制成的透明球体,半径为R.AB是竖直方向的直径.现有一束横截面为半径为R的细圆环的环形光束,沿AB方向射向球体,AB直径为光束的中心轴线.所有的光线经折射后恰好经过B点,从B点射出的光在水平光屏上形成一圆形亮环.水平光屏到B点的距离为L=R.求:
①球体材料的折射率;
②光屏上圆亮环的半径.
??
如图所示,一柱形玻璃的横截面是半径为R的圆弧,圆心O,以O为原点建立直角坐标系Oxy.一单色光平行于x轴射入玻璃,入射点的坐标为(0,d),单色光在玻璃中的折射率为n=,不考虑单色光经圆弧面反射后的情况.
(i)当d多大时,该单色光在圆弧面上刚好发生全反射?
(ii)当d→0时,求该单色光照射到x轴上的坐标.(θ很小时,sinθ≈θ,tanθ≈θ)
如图所示的玻璃砖左侧为矩形ABCD,AD边长为R,AB边长为2R;右侧为四分之一圆周形,半径为R.一束平行于CD边的单色光线自右侧的E点射向玻璃砖,进入玻璃砖后在CD的中点O经过一次反射,然后自AD边的F点射出,已知D、F两点间的距离为R,光在真空中的传播速度为c,求:
①该单色光对此玻璃砖的折射率;
②该光线在此玻璃砖中传播的时间。
如图所示,在双缝干涉实验中,S1和S2为双缝,P是光屏上的一点,已知P点与S1和S2距离之差为2.1×10-6m,今分别用A、B两种单色光在空气中做双缝干涉实验,问P点是亮条纹还是暗条纹?
(1)已知A光在折射率为n=1.5的介质中波长为4×10-7m;
(2)已知B光在某种介质中波长为3.15×10-7m,当B光从这种介质射向空气时,临界角为37°(sin
37°=0.6,cos
37°=0.8);
答案和解析
1.【答案】解:①光路如图
根据全反射定律:sinC=?????????…①
解得????C=60°??????????…②
由几何关系得r=30°????…③
n=????????????…④
得?sini=??????????…⑤
②v==×108m/s???????…⑥
由几何关系得?x=????…⑦
而??t=?????…⑧
解得??t=2×10-9s?????…⑨
答:(1)光在AB面的入射角的正弦值为;
(2)光从O点入射到AC面上发生全反射所经历的时间为2×10-9s。
【解析】①单色光恰好在AC面上发生全反射,在AC面上的入射角恰好等于临界角C.先根据临界角公式sinC=,求得C,再由几何关系求得光线在AB面的折射角,即可由折射定律求解光在AB面的入射角的正弦值;
②光在棱镜中的传播速度由公式v=求解,进而得到经历时间。
对于几何光学问题,往往是折射定律、全反射临界角公式、光速公式和几何知识的综合应用,解答的基础是正确画出光路图,理清各个角度的关系,再进行研究。
2.【答案】解:①作出光路图如图所示,由几何关系知:
Rsinα=R,即:α=60°
由图知,α=2β,得β=30°
由折射定律有:n==
②由几何知识可得:光屏上圆亮环的半径为:
r=Ltanα=Rtan60°=R
答:①球体材料的折射率是;
②光屏上圆亮环的半径是R.
【解析】①作出光路图,由几何关系求出入射角和折射角,根据折射定律求解折射率.
②结合几何关系求出光屏上圆亮环的半径.
解决几何光学问题的关键画出光路图,结合折射定律和几何关系进行求解.
3.【答案】解:
?(i)如图答图1,当光射到圆弧面上的入射角等于临界角C时刚好发生全反射,则
??
sinθ==
解得
θ=45°
根据几何关系得d=Rsin45°=R
(ii)如图答2,当射到圆弧面上的入射角很小时,设折射角为α,入射角为β,由折射定律得:
??n=
在△OEF中,由正弦定理得=
当d→0时,sinθ≈θ,则得OF=R,α=nβ
联立解得OF=(2)R。
答:
(i)当d是R时,该单色光在圆弧面上刚好发生全反射;
(ii)当d→0时,该单色光照射到x轴上的坐标为(2)R。
【解析】?
?
本题的关键是作出光路图,运用几何知识辅助分析,结合折射定律和数学知识进行求解。
(i)当光射到圆弧面上时入射角等于临界角C时,恰好发生全反射.由sinC=求出临界角C,再由几何知识求d;
(ii)当d→0时,光射到圆弧面上的入射角很小,在圆弧面上发生折射,由折射定律列式,结合正弦定理求解即可。
4.【答案】解:①该单色光在玻璃砖中的光路如图所示,有:tanα==
解得:α=30°
由几何知识得在E点的入射角为:i1=60°,折射角为:i2=30°
得该单色光对此玻璃砖的折射率为:
n==
②由n=知该单色光在此玻璃砖中的传播速度为:v=
OF==
OE=2Rcos30°=R
该单色光在此玻璃砖中的路程为:x=OF+OE=R
该单色光在此玻璃砖中传播的时间为:t==
答:①该单色光对此玻璃砖的折射率是;
②该光线在此玻璃砖中传播的时间是。
【解析】①画出光路图,由几何关系求得入射角和折射角,根据折射定律可求得折射率;
②根据n=求得该单色光在此玻璃砖中的传播速度,再由几何关系求得光在玻璃中的传播距离,则传播时间可求解。
解决本题关键是作出光路图,再运用几何知识求解入射角折射角,要掌握几何光学常用的三个规律:折射定律n=、临界角公式sinC=和光速公式v=。
5.【答案】解:(1)设A光在空气中波长为λA,在介质中波长为λA',
由n===得,
?λA=nλA'=1.5×4×10-7m=6×10-7m.
根据光程差:δ=2.1×10-6m=(3+)λA,
知A光在P点是暗条纹
(2)设B光在空气中波长为λB,在介质中波长为λB',由n'=得,λB=n'λB',
又临界角C=37°所以n'=
所以λB==?m=5.25×10-7?m
根据光程差:δ=2.1×10-6?m=4λB知,B光在P点是亮条纹
【解析】解决本题的关键掌握形成明条纹或暗条纹的条件、折射率与波长的关系等等知识,基础题。
已知P点与S1和S2的距离之差,由出现亮暗的条件可判断是亮条纹或暗条纹.根据n=,v=λf,频率f相等,求出A光在空气中的波长;
对于B光,根据临界角公式sinC=求出折射率,再用同样的方法求出B光在空气中的波长.再判断是亮条纹还是暗条纹。
第2页,共2页
第1页,共1页
同课章节目录
