新人教版七年级上册第二章《整式的加减》导学案
文档属性
| 名称 | 新人教版七年级上册第二章《整式的加减》导学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 128.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-12 00:00:00 | ||
图片预览



文档简介
课题:整式(1)单项式
【学习目标】:1.掌握代数式的正确抒写方式
2.理解单项式及单项式系数、次数的概念。
3.会准确迅速地确定一个单项式的系数和次数。
【自主学习】:(阅读教科书第54—56页,2.1整式,并完成下列填空)
1.下列说法或书写是否正确:
①1x ②-1x ③a×3 ④a÷2 ⑤
⑥b的系数为1,次数为0 ⑦ 的系数为2,次数为2
2.单项式:即由_________与______的乘积组成的代数式称为单项式。
补充: 单独_________或___________也是单项式,如a,5。
3.练习:判断下列各代数式哪些是单项式?
(1); (2)abc; (3)b2; (4)-5ab2; (5)y+x; (6)-xy2; (7)-5。
解:是单项式的有(填序号):________________________
4.单项式系数和次数:
四个单项式a2h,2πr,abc,-m中,请说出它们的数字因数和字母因数分别是什么?
单项式 a2h 2πr abc -m
数字因数
字母因数
小结:一个单项式中,单项式中的数字因数称为这个单项式的________一个单项式中,_____________的指数的和叫做这个单项式的次数。
注意点:
①圆周率π是常数;
②当一个单项式的系数是1或-1时,“1” 通常省略不写,如x2,-a2b等;
③单项式次数只与字母指数有关
【限时练习】:
(一).判断下列各代数式是否是单项式。如不是,请说明理由;如是,请写出它的系数和次数。
①x+1; ②; ③πr2; ④-a2b。
(二).下面各题的判断是否正确?
①-7xy2的系数是7;( ) ②-x2y3与x3没有系数;( )
③-ab3c2的次数是0+8+2;( ) ④-a3的系数是-1;( )
⑤-32x2y3的次数是7;( ) ⑥πr2h的系数是。( )
(三).选择题
1.下面说法中,正确的是( )
A.x的系数为0 B.x的次数为0 C.的系数为1 D.的次数为1
2.下面说法中,正确的是( )
A.xy+1是单项式 B.是单项式 C.是单项式 D.是单项式
3.单项式-ab2c3的系数和次数分别是( )
A.系数为-1,次数为3 B.系数为-1,次数为5
C.系数为-1,次数为6 D.以上说法都不对
4. ,x+1, -2,, 0.72xy,各式中单项式的个数是( )
A. 2个 B.3个 C.4个 D.5个
5.单项式-x2yz2的系数、次数分别是( )
A. 0,2 B. 0, 4 . C. -1,5 D.1,4
(四)、填空题
1.整式3x,-ab,t+1,0.12h+b中,单项式有_________,
2.长方形的宽为a,长为b,则周长为_________,面积为________
(五)、解答题
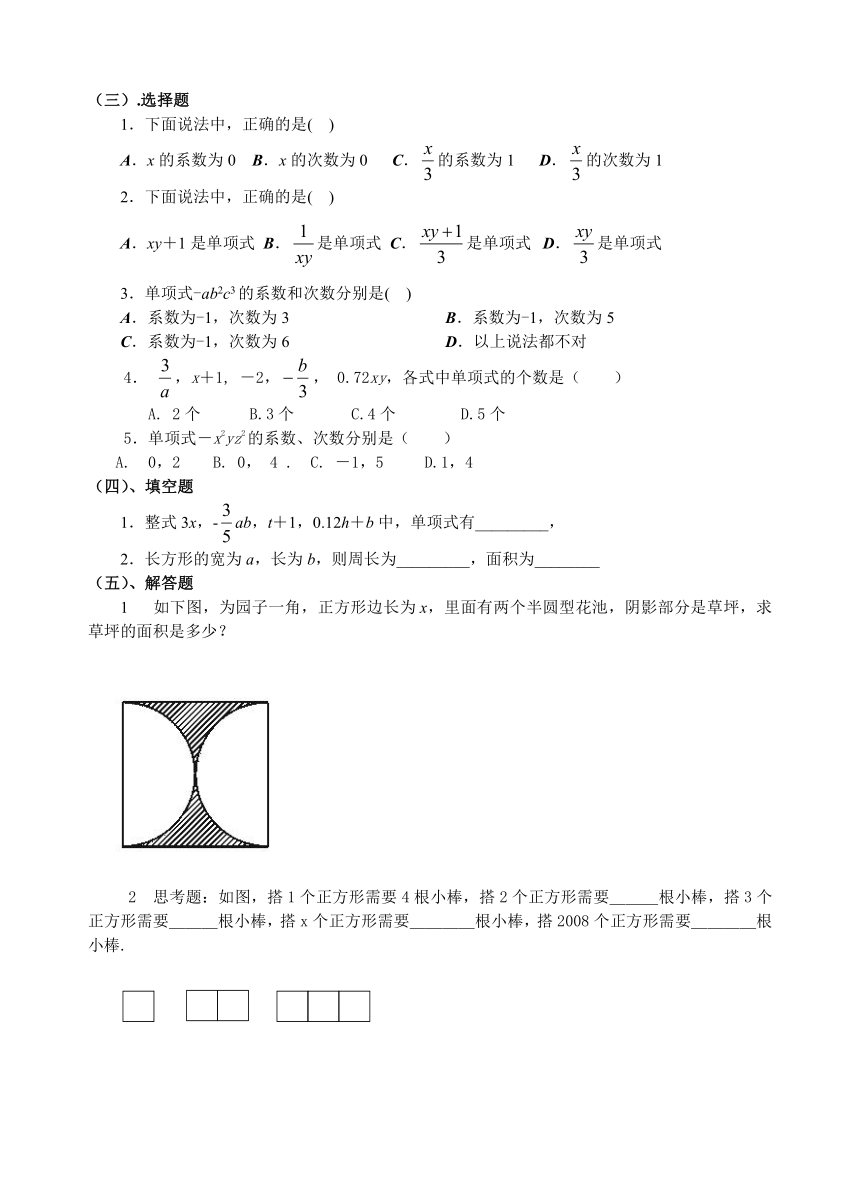
1 如下图,为园子一角,正方形边长为x,里面有两个半圆型花池,阴影部分是草坪,求草坪的面积是多少?
2 思考题:如图,搭1个正方形需要4根小棒,搭2个正方形需要___根小棒,搭3个正方形需要___根小棒,搭x个正方形需要____根小棒,搭2008个正方形需要____根小棒.
课题:整式(2) 多项式
【学习目标】:1.通过本节课的学习,使学生掌握整式多项式的项及其次数、常数项的概念。
2.能确定一个多项式的项数及其次数。
【课前小测】(5分钟):
1.下列结论中正确的是( )
A.没有加减运算的代数式一定是单项式 B.单项式的系数是,次数是3
C.单项式-a既没有系数,也没有次数 D.是2次单项式
2.组成多项式xy - 6x2y -12xy3+14的各项是 ( )
A. xy ,- 6x2y ,-12xy3 B. xy , 6x2y ,12xy3,14
C. xy, - 6x2y, -12xy3,14D. 以上答案都不对
3.单项式的系数是 ,次数是 ,是 次单项式.
4.在代数式a,-mn,5,,,7p中单项式有________个。
5.系数为-5,含有字母m、n的4次单项式有_____个,它们是 ___________________。
二、自主探究(阅读课本56-59页完成下列问题):
1、_______________的和叫做多项式。在多项式中,每个单项式叫做多项式的___。其中,不含字母的项,叫做_______。
例如多项式有_____项,它们是______________。其中常数项是________。
一个多项式含有几项,就叫几项式。多项式里________________________,叫做这个多项式的次数。例如,多项式是一个____次______项式。
注意事项:(1)多项式的次数不是所有项的次数之和;
(2)多项式的每一项都包括它前面的符号。
2、__________与___________统称为整式。
三、【限时训练】:
(一)、填空题:
(1)几个单项式的 ,叫做 .
(2) 和 统称整式.
(3)多项式2x4-3x5-5是 次 项式,最高次项的系数是 ,四次项的系数是 ,常数项是 .
(4)多项式a3-3ab2+3a2b-b3是 次 项式,它的各项的次数都是 .
(5).-a2b-ab+1是 次 项式,其中三次项系数是 ,二次项为 ,常数项为 ,写出所有的项 。
(6).如果为四次单项式,则m=____;
(7)把下列代数式,分别填在相应的集合中:-5a2,-ab,-,a2-2ab,,1-,;
单项式集合:{ …} 多项式集合:{ …}
整 式集合:{ …}
(8).三个连续偶数中,n是最小的一个,这三个数的和为 .
(9)已知轮船在逆水中前进的速度是千米/时,水流的速度是2千米/时,则这轮船在静水中航行的速度是 千米/时.
(二).判断题(对的画“√”,错的画“×”)
(1)是整式;( ) (2)单项式6ab3的系数是6,次数是4;( )
(3)是多项式;( )
(三)选择题
(1)单项式-xy2z3的系数和次数分别是( ).
A.-1,5 B.0,6 C.-1,6 D.0,5
(2)多项式-x2-x-1的各项分别是( )
A.-x2, x,1; B.-x2,-x,-1; C.x2, x,1; D.以上答案都不对.
(3)下列说法正确的是( ).
A.不是单项式; B.是单项式 C.x的系数是0;D.是整式.
(4)如果一个多项式是五次多项式,那么( )
A.这个多项式最多有六项;ww w.xkb 1.co m ( http: / / www.xkb1.com / )
B.这个多项式只能有一项的次数是六;
C.这个多项式一定是五次六项式;
D.这个多项式最少有二项,并且最高次项的次数是五.
(四)解答题
1.一辆汽车以x千米/小时行驶d 千米路程,若速度加快10千米/小时,则可少用多少小时?
2.已知代数式3xn-(m-1)x+1是关于x的三次二项式,求m、n的条件。
课题:整式的加减(1) 同类项
【学习目标】:1.理解同类项的概念,理解合并同类项的概念
2.熟练掌握根据合并两个同类项的法则进行计算化简
【课前小测】:(5分钟)
1.填空:
(1)多项式3-m2的项是_________,最高次项是__,常数项是___,次数是___;
(2)温度由-3度下降t度后是___度;
(3)一个数比x的2倍小3,则这个数为______;
(4)a与b两数平方的和为______;
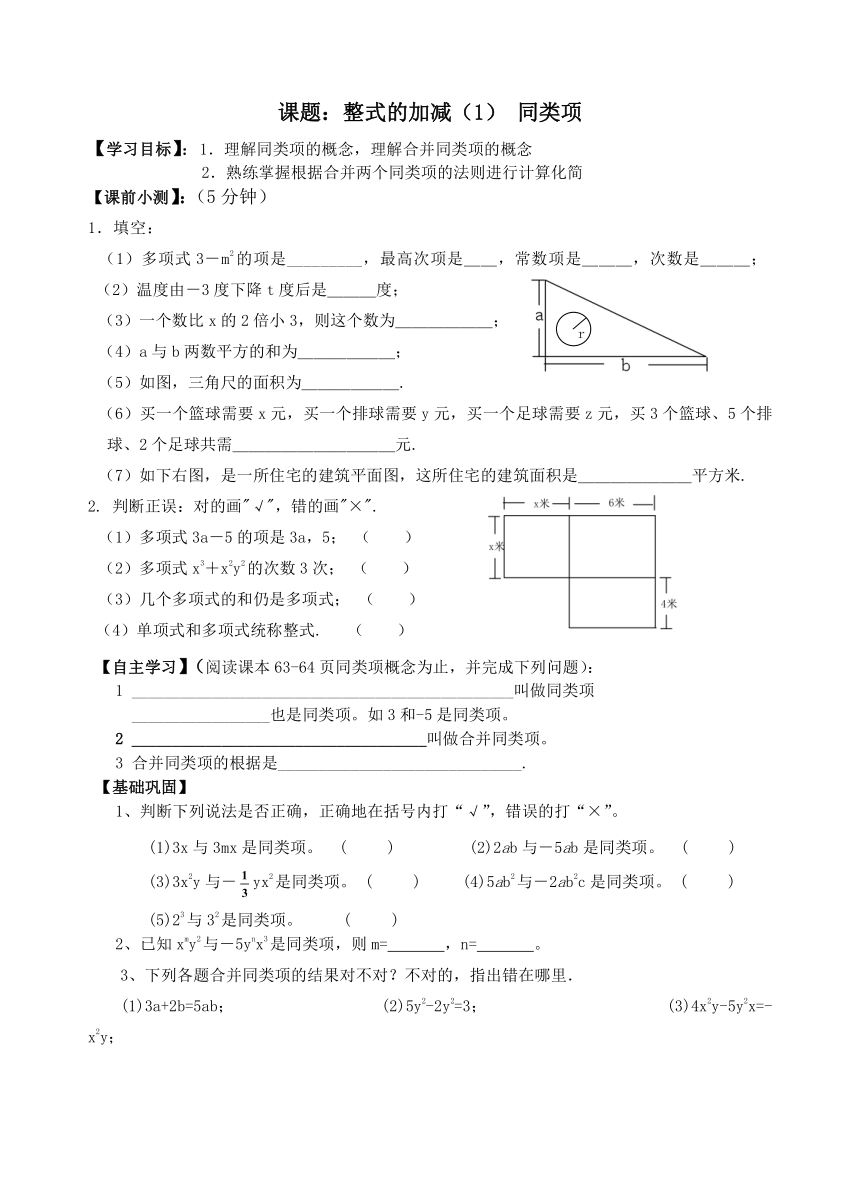
(5)如图,三角尺的面积为______.
(6)买一个篮球需要x元,买一个排球需要y元,买一个足球需要z元,买3个篮球、5个排球、2个足球共需__________元.
(7)如下右图,是一所住宅的建筑平面图,这所住宅的建筑面积是_______平方米.
2. 判断正误:对的画"√",错的画"×".
(1)多项式3a-5的项是3a,5; ( )
(2)多项式x3+x2y2的次数3次; ( )
(3)几个多项式的和仍是多项式; ( )
(4)单项式和多项式统称整式. ( )
【自主学习】(阅读课本63-64页同类项概念为止,并完成下列问题):
1 _______________________________________________叫做同类项
_________________也是同类项。如3和-5是同类项。
2 ____________________________________叫做合并同类项。
3 合并同类项的根据是______________________________.
【基础巩固】
1、判断下列说法是否正确,正确地在括号内打“√”,错误的打“×”。
(1)3x与3mx是同类项。 ( ) (2)2ab与-5ab是同类项。 ( )
(3)3x2y与-yx2是同类项。 ( ) (4)5ab2与-2ab2c是同类项。 ( )
(5)23与32是同类项。 ( )
2、已知xmy2与-5ynx3是同类项,则m= ,n= 。
3、下列各题合并同类项的结果对不对?不对的,指出错在哪里.
(1)3a+2b=5ab; (2)5y2-2y2=3; (3)4x2y-5y2x=-x2y;
(4)a+a=2a; (5)7ab-7ba=0; (6)3x2+2x3=5x5.
4、合并下列各式中的同类项:
(1)15x+4x-10x; (2)-6ab+ba+8ab; (3)-p2-p2-p2;
【限时训练】:
1.找出多项式4x2-8x+5-3x2+6x-2中的同类项:
(1)4x2与____是同类项;
(2)-8x与____是同类项;
(3)5与____是同类项.
2.填空并指出根据:
(1)6x-4x=(____)x=____;
(2)-7ab+6ab=(___)ab=____;
(3)10y2+y2=(____)y2=____;
(4)-0.5a+2a-3.5a=(______)a=____.
3.合并下列各式的同类项:
(1)-8x2-7x2= (2)xy-xy=
(3)-4a2b+4a2b= (4)y-y+2y=
(5)-3x2y+2x2y= (6)3xy2-2xy2=
(7)2x2+x2-3x2= (8)(x+y)3-2(x+y)3=
4.思考题:如图,大圆的半径是R,小圆的面积是大圆面积的,则阴影部分的面积为多少?
5.非典时期,同学们积极做网页歌颂白衣战士,一班同学做了x张,二班比一班的2倍少y张,二班做了_________张,两个班共做了_________张.
6. (备选题)求下列多项式的值。
其中
课题:整式的加减(2)合并同类项
【学习目标】:1 熟练找出在三项式以上中的各类同类项及合并化简
2 会按升(降)幂排列所给代数式
【课前小测】:(5分钟)
1.判断下列各组的两项是不是同类项:
(1)12x与2x; ( ) (2)2x2y与-5x2y ( )
(3)2a与a2; ( ) (4)4xy与5yx; ( )
(5)4abc与4ab;( ) (6)7xy2与7x2y; ( )
(7)a3与53; ( ) (8)-25与12. ( )
2.下列各题合并同类项的结果对不对?若不对,请改正。
(1)2x2+3x2=5x4;( ) (2)3x+2y=5xy; ( )
(3)7x2-3x2=4; ( ) (4)9a2b-9ba2=0; ( )
3.已知单项式3与-是同类项,那么= ,n=
4. 判断正误:对的画“√”,错的画“×”.
(1)a+b=b+a; ( )
(2)a-b=b-a; ( )
(3)a-b=-b+a; ( )
(4)x2+2-x=x2+x-2; ( )
(5)x2+2-x=x2-x+2; ( )
(6)x2+2-x=x+2-x2; ( )
(7)x2+2-x=-x+2+x2. ( )
【自主学习】(20分钟,阅读课本64倒数第三段-66页例3为止内容,完成下列问题):
布置思考:
1.思考:具备什么特点的多项式可以合并呢?
2.思考:交换项的位置时应注意什么事项?
3.什么是升幂排列与降幂排列?
【限时训练】:
1.合并下列多项式的同类项:
(1)8a+2b-5a-b (2)8x-3y+z-4x-3y+2z
2.合并下列各式的同类项:
(1)a2-3a+8-3a2+5a-7 (2)-3x2y-2xy2+3xy2+2x2y
(3)4a2+3b2+2ab-4a2-4b2( (4)2x2-5x+x2+4x-3x2-2
3.把多项式-5x2-6x4+2x-x3+5按字母x的升幂排列为: .
4. 求多项式3x2+4x-2x2-x+x2-3x-1的值,其中x=-3。
5.求多项式a2b-6ab-3a2b+5ab+2a2b的值,其中a=0.1,b=0.01;
6.某村土豆种植面积是a亩,白菜种植面积比土豆种植面积少8亩,青稞种植面积是土豆种植面积的10倍少7亩,问该村土豆、白菜、青稞一共种植多少亩.
7.(备选)某工厂第一车间有人,第二车间比第一车间人数的少30人,如果从第二车间调出10人到第一车间,那么:
(1)两个车间共有多少人?
(2)调动后,第一车间的人数比第二车间多多少人?
课题:整式的加减(3) 去括号
【学习目标】:能运用运算律探究去括号法则,并且利用去括号法则将整式化简。
【课前小测】:(5分钟)
1.合并同类项:
(1) (2) (3) (4)
(5) -5a+3a-2-3a-7 (6)
【自主学习】(15分钟,阅读课本66页-68页为止内容,完成下列问题):
去括号的法则:
法则1: 如果括号外的因数是正数,______________________________________.
法则2: 如果括号外的因数是负数,______________________________________。
特别地,+(x-3)与-(x-3)可以分别看作1与-1分别乘(x-3);
【要点归纳】:去括号时,特别是括号前面是“-”号时,括号连同括号前面的“-”号去掉,括号里的各项都改变符号.去括号规律可以简单记为“-”变“+”不变,要变全都变.当括号前带有数字因数时,这个数字要乘以括号内的每一项,切勿漏乘某些项.
【限时训练】:
1 去括号:
(1)a+(b-c)=_____________; (2)a-(b-c)=__________________;
(3)a-(-b+c)=______________; (4)a+(-b+c)=_____________;
(5)(a+b)-c=________________; (6)-(a+b)-c=_____________
2.化简:
(1)12(x-0.5)=
(2)-5(1-x)=
(3)-5a+(3a-2)-(3a-7)=
(4)(9y-3)+2(y+1) =
3.下列各式化简正确的是( )。
A.a-(2a-b+c)=-a-b+c B.(a+b)-(-b+c)=a+2b+c
C.3a-[5b-(2c-a)]=2a-5b+2c D.a-(b+c)-d=a-b+c-d
4.下面去括号错误的是( ).
A.a2-(a-b+c)=a2-a+b-c B.5+a-2(3a-5)=5+a-6a+5
C.3a-(3a2 - 2a)=3a-a2+a D.a3-[(a2-(-b))=a3-a2-b
5.计算:(1) 3(-2+3)-(2-)
(2).一个多项式与多项式-2+1的和是3-2,求这个多项式。
6.长方形的长是,宽是,求它的周长
7.计算:5xy2-[3xy2-(4xy2-2x2y)]+2x2y-xy2. (一般地,先去小括号,再去中括号。)
8.先化简,再求值:,其中
课题:整式的加减(4)
【学习目标】:能灵活运用整式的加减的步骤、方法进行运算。
【课前小测】:
1.判断正误:对的画“√”,错的画“×”.
(1)a-(b-c+d)=a-b-c+d; ( )
(2)a-(b+c)-d=a-b-c-d; ( )
(3)(a+b) -(-c+d)=a+b-c-d; ( )
(4)a+(-b+c-d)=a-b+c-d; ( )
(5)-(a-b)+(c-d)=-a+b-c+d. ( )
2.计算: (1) (2)
3.已知,,求的值。
【自主学习】(首先独立完成下列例6—例9,然后再对照书本解答检验是否正确)
例6.计算:(1)(2x-3y)+(5x+4y) (2)(8a-7b)-(4a-5b).
例7.一种笔记本的单价是x(元),圆珠笔的单价是y(元),小红买这种笔记本3本,买圆珠笔2枝;小明买这种笔记本4个,买圆珠笔3枝,买这些笔记本和圆珠笔,小红和小明共花费多少钱?
长 宽 高
小纸盒 a b c
大纸盒 1.5a 2b 2c
例8.做大小两个长方体纸盒,尺寸如下(单位:厘米).
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比小纸盒多用料多少平方厘米?
(学生小组学习,讨论解题方法.)
归纳:一般地,几个整式相加减步骤:_________________________________________.
例9.求x-2(x-y2)+(-x+y2)的值,其中x=-2,y=.
(思路点拨:先去括号,合并同类项化简后,再代入数值进行计算比较简便,去括号时,特别注意符号问题。)
【要点归纳】:
1.整式的加减实际上就是去括号、合并同类项这两个知识的综合。
2.整式的加减的一般步骤:
①如果有括号,那么先算括号。②如果有同类项,则合并同类项。
3.求多项式的值,一般先将多项式化简再代入求值,这样使计算简便。
【限时训练】:
1.如果a-b=,那么-3(b-a)的值是( ).
A.- B.HYPERLINK "http://www./" C. D.
2.一个多项式与x2-2x+1的和是3x-2,则这个多项式为( ).
A.x2-5x+3 B.-x2+x-1 C.-x2+5x-3 D.x2-5x-13
3.填空:整式x+y与整式x-y的和为 ,差为 .
4.计算:
(1)(-x+2x2+5)+(4x2-3-6x);
(2)(3a2-ab+7)-(-4a2+2ab+7);
(3)(2a-3b)-[4a+(3a-b)].
5.先化简下式,再求值:
(1) 5(3a2b-ab2)-(ab2+3a2b),其中a=,b=.
(2) 4x2y-[6xy-3(4xy-2)-x2y]+1,其中x=2,y=-;
课题:第二章 整式的加减复习(两课时)
【复习目标】: 1. 进一步理解单项式、多项式、整式及其有关概念,准确确定单项式的系数、次数、多项式的项、次数;
2.理解同类项概念,掌握合并同类项法则和去括号规律,熟练地进行整式加减。
【重点难点】:整式加减运算
【导学指导】
一、知识回顾
1、______和______统称整式。
(1)单项式:由 与 的乘积式子称为单项式。单独一个数或一个字母也是单项式,如a ,5。
单项式的系数:单式项里的 叫做单项式的系数
单项式的次数:单项式中 叫做单项式的次数
(2)多项式:几个 的和叫做多项式。其中,每个单项式叫做多项式的 ,不含字母的项叫做 。
多项式的次数:多项式里 的次数,叫做多项式的次数
2、同类项:必须同时具备的两个条件(缺一不可):
①所含的 相同; ②相同 也相同
合并同类项:就是把多项式中的同类项合并成一项。
方法:把各项的 相加,而 不变。
3、去括号法则
法则1:
法则2:
去括号法则的依据实际是 。
4、整式的加减
整式的加减的运算法则:如遇到括号,则先 ,再 ;
5、本章需要注意的几个问题
①整式(既单项式和多项式)中,分母一律不能含有字母。
②π不是字母,而是一个数字,
③多项式相加(减)时,必须用括号把多项式括起来,才能进行计算。
④去括号时,要特别注意括号前面的因数。
二、【限时练习】
1、在,中,单项式有:
多项式有: ,整式有: .
2、已知-7x2ym是7次单项式则m=
3、一种商品每件a元,按成本增加20%定出的价格是 ;后来因库存积压,又以原价的八五折出售,则现价是 元;每件还能盈利 元。
4.单项式-的系数是 ,次数是 ;
5.已知-5xmy3与4x3yn能合并,则mn = 。
6、7-2xy-3x2y3+5x3y2z-9x4y3z2是 次 项式,其中最高次项是 ,最高次项的系数是 ,常数项是 ,是按字母 作 幂排列。
8、已知x-y=5,xy=3,则3xy-7x+7y= 。
9、已知A=3x+1,B=6x-3,则3A-B= 。
10.已知单项式3与-的和是单项式,那么= ,n=
11.化简3-2(-3)的结果是 .
12.计算:
(1)3(xy2-x2y)-2(xy+xy2)+3x2y; (2)5a2-[a2+(5a2-2a)-2(a2-3a)];
思路点拨:整式加减运算,有括号时,应先去括号,再合并同类项,多种括号时,一般地先去小括号,再去中括号,最后再去大括号.
解:(1)原式= (2)原式=
13、求5ab-2[3ab- (4ab2+ab)] -5ab2的值,其中a=,b=-;
14.电影院第1排有a个座位,后面每排都比前一排多1个座位,第2排有多少个座位?第3排呢?用m表示第n排座位数,m是多少?当a=20,n=19时,计算m的值.
15、某中学3名老师带18名学生,门票每张a元,有两种购买方式:第一种是老师每人a元,学生半价;第二种是不论老师学生一律七五折,请你帮他们算一下,按哪种方式购买门票比较省钱。
【拓展训练】:
1.多项式2--4,它的项数为 ,次数是 ;
2.已知轮船在逆水中前进的速度是千米/时,水流的速度是2千米/时,则这轮船在静水中航行的速度是 千米/时。
3.计算: x-2(1-2x+x2)+3(-2+3x-x2)
4.已知ab=3,a+b=4,求3ab-[2a - (2ab-2b)+3]的值。
5、已知:(x+2)2+|y+1|=0,求5xy2-2x2y-[3xy2-(4xy2-2x2y)]的值。
6有这样一道题:“当时,求多项式的值.”有一位同学指出,题目中给出的条件与是多余的,他的说法有道理吗?请加以说明。
7、若(x2+ax-2y+7)―(bx2―2x+9 y-1)的值与字母x的取值无关,求a、b的值。
8.用式子表示十位上的数是a,个位上的数是b的两位数,再把这个两位数的十位上的数与个位上的数交换位置,计算所得的数与原数的和,这个数能被11整除吗?
9.大客车上原有人,中途有一半人下车,又上车若干人,此时车上共有乘客人,请问中途上车的共有多少人?当时,中途上车的乘客有多少人?
10.某学生由于看错了运算符号,把一个整式减去多项式误认为是加上这个多项式,结果得出的答案是,求原题的正确答案。
第二章 整式加减检测试卷(满分100分)
班级___________姓名_____________分数_____________
一、填空题(每小题4分,共32分)
1、“的平方与2的差”用代数式表示为___________。
2、单项式的系数是___________ ,次数是______________。
3、多项式是________次_________项式,常数项是___________。
4、若和是同类项,则m=_________,n=___________。
5、如果+=0,那么=____________。
6、如果代数式的值是3,则代数式的值是___________。
7、与多项式的和是的多项式是______________。
8、飞机的无风飞行航速为千米/时,风速为20千米/时.则飞机顺风飞行4小时的行程是__________千米;飞机逆风飞行3小时的行程是__________千米。
二、选择题(每小题4分,共24分)
9、在下列代数式:中,单项式有( )
A.3个 B.4个 C.5个 D.6个
10、下列各项式中,是二次三项式的是 ( )
A、 B、 C、 D、
11、下面计算正确的是( )
A.3-=3 B.3+2=5
C.3+=3 D.-0.25+=0
12、化简的结果为( )
A. B. C. D.
13、三个连续奇数的第一个是n,则三个连续奇数的和是 ( )
A、 B、 C、 D、
14.两个四次多项式的和的次数是( )
A.八次 B.四次 C.不低于四次 D.不高于四次
三、解答题
15、化简下列各式。(每小题7分,共14分)
(1) (2) ;
16、先化简,再求值.(每小题10分,共20分)
(1),其中;
(2);
17、(10分)有这样一道题:
“时,求多项式
的值”,马小虎做题时把错抄成,王小真没抄错题,但他们做出的结果却都一样,你知道这是怎么回事吗?说明理由.
【学习目标】:1.掌握代数式的正确抒写方式
2.理解单项式及单项式系数、次数的概念。
3.会准确迅速地确定一个单项式的系数和次数。
【自主学习】:(阅读教科书第54—56页,2.1整式,并完成下列填空)
1.下列说法或书写是否正确:
①1x ②-1x ③a×3 ④a÷2 ⑤
⑥b的系数为1,次数为0 ⑦ 的系数为2,次数为2
2.单项式:即由_________与______的乘积组成的代数式称为单项式。
补充: 单独_________或___________也是单项式,如a,5。
3.练习:判断下列各代数式哪些是单项式?
(1); (2)abc; (3)b2; (4)-5ab2; (5)y+x; (6)-xy2; (7)-5。
解:是单项式的有(填序号):________________________
4.单项式系数和次数:
四个单项式a2h,2πr,abc,-m中,请说出它们的数字因数和字母因数分别是什么?
单项式 a2h 2πr abc -m
数字因数
字母因数
小结:一个单项式中,单项式中的数字因数称为这个单项式的________一个单项式中,_____________的指数的和叫做这个单项式的次数。
注意点:
①圆周率π是常数;
②当一个单项式的系数是1或-1时,“1” 通常省略不写,如x2,-a2b等;
③单项式次数只与字母指数有关
【限时练习】:
(一).判断下列各代数式是否是单项式。如不是,请说明理由;如是,请写出它的系数和次数。
①x+1; ②; ③πr2; ④-a2b。
(二).下面各题的判断是否正确?
①-7xy2的系数是7;( ) ②-x2y3与x3没有系数;( )
③-ab3c2的次数是0+8+2;( ) ④-a3的系数是-1;( )
⑤-32x2y3的次数是7;( ) ⑥πr2h的系数是。( )
(三).选择题
1.下面说法中,正确的是( )
A.x的系数为0 B.x的次数为0 C.的系数为1 D.的次数为1
2.下面说法中,正确的是( )
A.xy+1是单项式 B.是单项式 C.是单项式 D.是单项式
3.单项式-ab2c3的系数和次数分别是( )
A.系数为-1,次数为3 B.系数为-1,次数为5
C.系数为-1,次数为6 D.以上说法都不对
4. ,x+1, -2,, 0.72xy,各式中单项式的个数是( )
A. 2个 B.3个 C.4个 D.5个
5.单项式-x2yz2的系数、次数分别是( )
A. 0,2 B. 0, 4 . C. -1,5 D.1,4
(四)、填空题
1.整式3x,-ab,t+1,0.12h+b中,单项式有_________,
2.长方形的宽为a,长为b,则周长为_________,面积为________
(五)、解答题
1 如下图,为园子一角,正方形边长为x,里面有两个半圆型花池,阴影部分是草坪,求草坪的面积是多少?
2 思考题:如图,搭1个正方形需要4根小棒,搭2个正方形需要___根小棒,搭3个正方形需要___根小棒,搭x个正方形需要____根小棒,搭2008个正方形需要____根小棒.
课题:整式(2) 多项式
【学习目标】:1.通过本节课的学习,使学生掌握整式多项式的项及其次数、常数项的概念。
2.能确定一个多项式的项数及其次数。
【课前小测】(5分钟):
1.下列结论中正确的是( )
A.没有加减运算的代数式一定是单项式 B.单项式的系数是,次数是3
C.单项式-a既没有系数,也没有次数 D.是2次单项式
2.组成多项式xy - 6x2y -12xy3+14的各项是 ( )
A. xy ,- 6x2y ,-12xy3 B. xy , 6x2y ,12xy3,14
C. xy, - 6x2y, -12xy3,14D. 以上答案都不对
3.单项式的系数是 ,次数是 ,是 次单项式.
4.在代数式a,-mn,5,,,7p中单项式有________个。
5.系数为-5,含有字母m、n的4次单项式有_____个,它们是 ___________________。
二、自主探究(阅读课本56-59页完成下列问题):
1、_______________的和叫做多项式。在多项式中,每个单项式叫做多项式的___。其中,不含字母的项,叫做_______。
例如多项式有_____项,它们是______________。其中常数项是________。
一个多项式含有几项,就叫几项式。多项式里________________________,叫做这个多项式的次数。例如,多项式是一个____次______项式。
注意事项:(1)多项式的次数不是所有项的次数之和;
(2)多项式的每一项都包括它前面的符号。
2、__________与___________统称为整式。
三、【限时训练】:
(一)、填空题:
(1)几个单项式的 ,叫做 .
(2) 和 统称整式.
(3)多项式2x4-3x5-5是 次 项式,最高次项的系数是 ,四次项的系数是 ,常数项是 .
(4)多项式a3-3ab2+3a2b-b3是 次 项式,它的各项的次数都是 .
(5).-a2b-ab+1是 次 项式,其中三次项系数是 ,二次项为 ,常数项为 ,写出所有的项 。
(6).如果为四次单项式,则m=____;
(7)把下列代数式,分别填在相应的集合中:-5a2,-ab,-,a2-2ab,,1-,;
单项式集合:{ …} 多项式集合:{ …}
整 式集合:{ …}
(8).三个连续偶数中,n是最小的一个,这三个数的和为 .
(9)已知轮船在逆水中前进的速度是千米/时,水流的速度是2千米/时,则这轮船在静水中航行的速度是 千米/时.
(二).判断题(对的画“√”,错的画“×”)
(1)是整式;( ) (2)单项式6ab3的系数是6,次数是4;( )
(3)是多项式;( )
(三)选择题
(1)单项式-xy2z3的系数和次数分别是( ).
A.-1,5 B.0,6 C.-1,6 D.0,5
(2)多项式-x2-x-1的各项分别是( )
A.-x2, x,1; B.-x2,-x,-1; C.x2, x,1; D.以上答案都不对.
(3)下列说法正确的是( ).
A.不是单项式; B.是单项式 C.x的系数是0;D.是整式.
(4)如果一个多项式是五次多项式,那么( )
A.这个多项式最多有六项;ww w.xkb 1.co m ( http: / / www.xkb1.com / )
B.这个多项式只能有一项的次数是六;
C.这个多项式一定是五次六项式;
D.这个多项式最少有二项,并且最高次项的次数是五.
(四)解答题
1.一辆汽车以x千米/小时行驶d 千米路程,若速度加快10千米/小时,则可少用多少小时?
2.已知代数式3xn-(m-1)x+1是关于x的三次二项式,求m、n的条件。
课题:整式的加减(1) 同类项
【学习目标】:1.理解同类项的概念,理解合并同类项的概念
2.熟练掌握根据合并两个同类项的法则进行计算化简
【课前小测】:(5分钟)
1.填空:
(1)多项式3-m2的项是_________,最高次项是__,常数项是___,次数是___;
(2)温度由-3度下降t度后是___度;
(3)一个数比x的2倍小3,则这个数为______;
(4)a与b两数平方的和为______;
(5)如图,三角尺的面积为______.
(6)买一个篮球需要x元,买一个排球需要y元,买一个足球需要z元,买3个篮球、5个排球、2个足球共需__________元.
(7)如下右图,是一所住宅的建筑平面图,这所住宅的建筑面积是_______平方米.
2. 判断正误:对的画"√",错的画"×".
(1)多项式3a-5的项是3a,5; ( )
(2)多项式x3+x2y2的次数3次; ( )
(3)几个多项式的和仍是多项式; ( )
(4)单项式和多项式统称整式. ( )
【自主学习】(阅读课本63-64页同类项概念为止,并完成下列问题):
1 _______________________________________________叫做同类项
_________________也是同类项。如3和-5是同类项。
2 ____________________________________叫做合并同类项。
3 合并同类项的根据是______________________________.
【基础巩固】
1、判断下列说法是否正确,正确地在括号内打“√”,错误的打“×”。
(1)3x与3mx是同类项。 ( ) (2)2ab与-5ab是同类项。 ( )
(3)3x2y与-yx2是同类项。 ( ) (4)5ab2与-2ab2c是同类项。 ( )
(5)23与32是同类项。 ( )
2、已知xmy2与-5ynx3是同类项,则m= ,n= 。
3、下列各题合并同类项的结果对不对?不对的,指出错在哪里.
(1)3a+2b=5ab; (2)5y2-2y2=3; (3)4x2y-5y2x=-x2y;
(4)a+a=2a; (5)7ab-7ba=0; (6)3x2+2x3=5x5.
4、合并下列各式中的同类项:
(1)15x+4x-10x; (2)-6ab+ba+8ab; (3)-p2-p2-p2;
【限时训练】:
1.找出多项式4x2-8x+5-3x2+6x-2中的同类项:
(1)4x2与____是同类项;
(2)-8x与____是同类项;
(3)5与____是同类项.
2.填空并指出根据:
(1)6x-4x=(____)x=____;
(2)-7ab+6ab=(___)ab=____;
(3)10y2+y2=(____)y2=____;
(4)-0.5a+2a-3.5a=(______)a=____.
3.合并下列各式的同类项:
(1)-8x2-7x2= (2)xy-xy=
(3)-4a2b+4a2b= (4)y-y+2y=
(5)-3x2y+2x2y= (6)3xy2-2xy2=
(7)2x2+x2-3x2= (8)(x+y)3-2(x+y)3=
4.思考题:如图,大圆的半径是R,小圆的面积是大圆面积的,则阴影部分的面积为多少?
5.非典时期,同学们积极做网页歌颂白衣战士,一班同学做了x张,二班比一班的2倍少y张,二班做了_________张,两个班共做了_________张.
6. (备选题)求下列多项式的值。
其中
课题:整式的加减(2)合并同类项
【学习目标】:1 熟练找出在三项式以上中的各类同类项及合并化简
2 会按升(降)幂排列所给代数式
【课前小测】:(5分钟)
1.判断下列各组的两项是不是同类项:
(1)12x与2x; ( ) (2)2x2y与-5x2y ( )
(3)2a与a2; ( ) (4)4xy与5yx; ( )
(5)4abc与4ab;( ) (6)7xy2与7x2y; ( )
(7)a3与53; ( ) (8)-25与12. ( )
2.下列各题合并同类项的结果对不对?若不对,请改正。
(1)2x2+3x2=5x4;( ) (2)3x+2y=5xy; ( )
(3)7x2-3x2=4; ( ) (4)9a2b-9ba2=0; ( )
3.已知单项式3与-是同类项,那么= ,n=
4. 判断正误:对的画“√”,错的画“×”.
(1)a+b=b+a; ( )
(2)a-b=b-a; ( )
(3)a-b=-b+a; ( )
(4)x2+2-x=x2+x-2; ( )
(5)x2+2-x=x2-x+2; ( )
(6)x2+2-x=x+2-x2; ( )
(7)x2+2-x=-x+2+x2. ( )
【自主学习】(20分钟,阅读课本64倒数第三段-66页例3为止内容,完成下列问题):
布置思考:
1.思考:具备什么特点的多项式可以合并呢?
2.思考:交换项的位置时应注意什么事项?
3.什么是升幂排列与降幂排列?
【限时训练】:
1.合并下列多项式的同类项:
(1)8a+2b-5a-b (2)8x-3y+z-4x-3y+2z
2.合并下列各式的同类项:
(1)a2-3a+8-3a2+5a-7 (2)-3x2y-2xy2+3xy2+2x2y
(3)4a2+3b2+2ab-4a2-4b2( (4)2x2-5x+x2+4x-3x2-2
3.把多项式-5x2-6x4+2x-x3+5按字母x的升幂排列为: .
4. 求多项式3x2+4x-2x2-x+x2-3x-1的值,其中x=-3。
5.求多项式a2b-6ab-3a2b+5ab+2a2b的值,其中a=0.1,b=0.01;
6.某村土豆种植面积是a亩,白菜种植面积比土豆种植面积少8亩,青稞种植面积是土豆种植面积的10倍少7亩,问该村土豆、白菜、青稞一共种植多少亩.
7.(备选)某工厂第一车间有人,第二车间比第一车间人数的少30人,如果从第二车间调出10人到第一车间,那么:
(1)两个车间共有多少人?
(2)调动后,第一车间的人数比第二车间多多少人?
课题:整式的加减(3) 去括号
【学习目标】:能运用运算律探究去括号法则,并且利用去括号法则将整式化简。
【课前小测】:(5分钟)
1.合并同类项:
(1) (2) (3) (4)
(5) -5a+3a-2-3a-7 (6)
【自主学习】(15分钟,阅读课本66页-68页为止内容,完成下列问题):
去括号的法则:
法则1: 如果括号外的因数是正数,______________________________________.
法则2: 如果括号外的因数是负数,______________________________________。
特别地,+(x-3)与-(x-3)可以分别看作1与-1分别乘(x-3);
【要点归纳】:去括号时,特别是括号前面是“-”号时,括号连同括号前面的“-”号去掉,括号里的各项都改变符号.去括号规律可以简单记为“-”变“+”不变,要变全都变.当括号前带有数字因数时,这个数字要乘以括号内的每一项,切勿漏乘某些项.
【限时训练】:
1 去括号:
(1)a+(b-c)=_____________; (2)a-(b-c)=__________________;
(3)a-(-b+c)=______________; (4)a+(-b+c)=_____________;
(5)(a+b)-c=________________; (6)-(a+b)-c=_____________
2.化简:
(1)12(x-0.5)=
(2)-5(1-x)=
(3)-5a+(3a-2)-(3a-7)=
(4)(9y-3)+2(y+1) =
3.下列各式化简正确的是( )。
A.a-(2a-b+c)=-a-b+c B.(a+b)-(-b+c)=a+2b+c
C.3a-[5b-(2c-a)]=2a-5b+2c D.a-(b+c)-d=a-b+c-d
4.下面去括号错误的是( ).
A.a2-(a-b+c)=a2-a+b-c B.5+a-2(3a-5)=5+a-6a+5
C.3a-(3a2 - 2a)=3a-a2+a D.a3-[(a2-(-b))=a3-a2-b
5.计算:(1) 3(-2+3)-(2-)
(2).一个多项式与多项式-2+1的和是3-2,求这个多项式。
6.长方形的长是,宽是,求它的周长
7.计算:5xy2-[3xy2-(4xy2-2x2y)]+2x2y-xy2. (一般地,先去小括号,再去中括号。)
8.先化简,再求值:,其中
课题:整式的加减(4)
【学习目标】:能灵活运用整式的加减的步骤、方法进行运算。
【课前小测】:
1.判断正误:对的画“√”,错的画“×”.
(1)a-(b-c+d)=a-b-c+d; ( )
(2)a-(b+c)-d=a-b-c-d; ( )
(3)(a+b) -(-c+d)=a+b-c-d; ( )
(4)a+(-b+c-d)=a-b+c-d; ( )
(5)-(a-b)+(c-d)=-a+b-c+d. ( )
2.计算: (1) (2)
3.已知,,求的值。
【自主学习】(首先独立完成下列例6—例9,然后再对照书本解答检验是否正确)
例6.计算:(1)(2x-3y)+(5x+4y) (2)(8a-7b)-(4a-5b).
例7.一种笔记本的单价是x(元),圆珠笔的单价是y(元),小红买这种笔记本3本,买圆珠笔2枝;小明买这种笔记本4个,买圆珠笔3枝,买这些笔记本和圆珠笔,小红和小明共花费多少钱?
长 宽 高
小纸盒 a b c
大纸盒 1.5a 2b 2c
例8.做大小两个长方体纸盒,尺寸如下(单位:厘米).
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比小纸盒多用料多少平方厘米?
(学生小组学习,讨论解题方法.)
归纳:一般地,几个整式相加减步骤:_________________________________________.
例9.求x-2(x-y2)+(-x+y2)的值,其中x=-2,y=.
(思路点拨:先去括号,合并同类项化简后,再代入数值进行计算比较简便,去括号时,特别注意符号问题。)
【要点归纳】:
1.整式的加减实际上就是去括号、合并同类项这两个知识的综合。
2.整式的加减的一般步骤:
①如果有括号,那么先算括号。②如果有同类项,则合并同类项。
3.求多项式的值,一般先将多项式化简再代入求值,这样使计算简便。
【限时训练】:
1.如果a-b=,那么-3(b-a)的值是( ).
A.- B.HYPERLINK "http://www./" C. D.
2.一个多项式与x2-2x+1的和是3x-2,则这个多项式为( ).
A.x2-5x+3 B.-x2+x-1 C.-x2+5x-3 D.x2-5x-13
3.填空:整式x+y与整式x-y的和为 ,差为 .
4.计算:
(1)(-x+2x2+5)+(4x2-3-6x);
(2)(3a2-ab+7)-(-4a2+2ab+7);
(3)(2a-3b)-[4a+(3a-b)].
5.先化简下式,再求值:
(1) 5(3a2b-ab2)-(ab2+3a2b),其中a=,b=.
(2) 4x2y-[6xy-3(4xy-2)-x2y]+1,其中x=2,y=-;
课题:第二章 整式的加减复习(两课时)
【复习目标】: 1. 进一步理解单项式、多项式、整式及其有关概念,准确确定单项式的系数、次数、多项式的项、次数;
2.理解同类项概念,掌握合并同类项法则和去括号规律,熟练地进行整式加减。
【重点难点】:整式加减运算
【导学指导】
一、知识回顾
1、______和______统称整式。
(1)单项式:由 与 的乘积式子称为单项式。单独一个数或一个字母也是单项式,如a ,5。
单项式的系数:单式项里的 叫做单项式的系数
单项式的次数:单项式中 叫做单项式的次数
(2)多项式:几个 的和叫做多项式。其中,每个单项式叫做多项式的 ,不含字母的项叫做 。
多项式的次数:多项式里 的次数,叫做多项式的次数
2、同类项:必须同时具备的两个条件(缺一不可):
①所含的 相同; ②相同 也相同
合并同类项:就是把多项式中的同类项合并成一项。
方法:把各项的 相加,而 不变。
3、去括号法则
法则1:
法则2:
去括号法则的依据实际是 。
4、整式的加减
整式的加减的运算法则:如遇到括号,则先 ,再 ;
5、本章需要注意的几个问题
①整式(既单项式和多项式)中,分母一律不能含有字母。
②π不是字母,而是一个数字,
③多项式相加(减)时,必须用括号把多项式括起来,才能进行计算。
④去括号时,要特别注意括号前面的因数。
二、【限时练习】
1、在,中,单项式有:
多项式有: ,整式有: .
2、已知-7x2ym是7次单项式则m=
3、一种商品每件a元,按成本增加20%定出的价格是 ;后来因库存积压,又以原价的八五折出售,则现价是 元;每件还能盈利 元。
4.单项式-的系数是 ,次数是 ;
5.已知-5xmy3与4x3yn能合并,则mn = 。
6、7-2xy-3x2y3+5x3y2z-9x4y3z2是 次 项式,其中最高次项是 ,最高次项的系数是 ,常数项是 ,是按字母 作 幂排列。
8、已知x-y=5,xy=3,则3xy-7x+7y= 。
9、已知A=3x+1,B=6x-3,则3A-B= 。
10.已知单项式3与-的和是单项式,那么= ,n=
11.化简3-2(-3)的结果是 .
12.计算:
(1)3(xy2-x2y)-2(xy+xy2)+3x2y; (2)5a2-[a2+(5a2-2a)-2(a2-3a)];
思路点拨:整式加减运算,有括号时,应先去括号,再合并同类项,多种括号时,一般地先去小括号,再去中括号,最后再去大括号.
解:(1)原式= (2)原式=
13、求5ab-2[3ab- (4ab2+ab)] -5ab2的值,其中a=,b=-;
14.电影院第1排有a个座位,后面每排都比前一排多1个座位,第2排有多少个座位?第3排呢?用m表示第n排座位数,m是多少?当a=20,n=19时,计算m的值.
15、某中学3名老师带18名学生,门票每张a元,有两种购买方式:第一种是老师每人a元,学生半价;第二种是不论老师学生一律七五折,请你帮他们算一下,按哪种方式购买门票比较省钱。
【拓展训练】:
1.多项式2--4,它的项数为 ,次数是 ;
2.已知轮船在逆水中前进的速度是千米/时,水流的速度是2千米/时,则这轮船在静水中航行的速度是 千米/时。
3.计算: x-2(1-2x+x2)+3(-2+3x-x2)
4.已知ab=3,a+b=4,求3ab-[2a - (2ab-2b)+3]的值。
5、已知:(x+2)2+|y+1|=0,求5xy2-2x2y-[3xy2-(4xy2-2x2y)]的值。
6有这样一道题:“当时,求多项式的值.”有一位同学指出,题目中给出的条件与是多余的,他的说法有道理吗?请加以说明。
7、若(x2+ax-2y+7)―(bx2―2x+9 y-1)的值与字母x的取值无关,求a、b的值。
8.用式子表示十位上的数是a,个位上的数是b的两位数,再把这个两位数的十位上的数与个位上的数交换位置,计算所得的数与原数的和,这个数能被11整除吗?
9.大客车上原有人,中途有一半人下车,又上车若干人,此时车上共有乘客人,请问中途上车的共有多少人?当时,中途上车的乘客有多少人?
10.某学生由于看错了运算符号,把一个整式减去多项式误认为是加上这个多项式,结果得出的答案是,求原题的正确答案。
第二章 整式加减检测试卷(满分100分)
班级___________姓名_____________分数_____________
一、填空题(每小题4分,共32分)
1、“的平方与2的差”用代数式表示为___________。
2、单项式的系数是___________ ,次数是______________。
3、多项式是________次_________项式,常数项是___________。
4、若和是同类项,则m=_________,n=___________。
5、如果+=0,那么=____________。
6、如果代数式的值是3,则代数式的值是___________。
7、与多项式的和是的多项式是______________。
8、飞机的无风飞行航速为千米/时,风速为20千米/时.则飞机顺风飞行4小时的行程是__________千米;飞机逆风飞行3小时的行程是__________千米。
二、选择题(每小题4分,共24分)
9、在下列代数式:中,单项式有( )
A.3个 B.4个 C.5个 D.6个
10、下列各项式中,是二次三项式的是 ( )
A、 B、 C、 D、
11、下面计算正确的是( )
A.3-=3 B.3+2=5
C.3+=3 D.-0.25+=0
12、化简的结果为( )
A. B. C. D.
13、三个连续奇数的第一个是n,则三个连续奇数的和是 ( )
A、 B、 C、 D、
14.两个四次多项式的和的次数是( )
A.八次 B.四次 C.不低于四次 D.不高于四次
三、解答题
15、化简下列各式。(每小题7分,共14分)
(1) (2) ;
16、先化简,再求值.(每小题10分,共20分)
(1),其中;
(2);
17、(10分)有这样一道题:
“时,求多项式
的值”,马小虎做题时把错抄成,王小真没抄错题,但他们做出的结果却都一样,你知道这是怎么回事吗?说明理由.
