人教高中数学必修四第二章《平面向量复习小结》-课件(28张ppt)
文档属性
| 名称 | 人教高中数学必修四第二章《平面向量复习小结》-课件(28张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-29 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
一、向量的基本概念
向量、零向量、单位向量、共线向量(平行向量)、相等向量、相反向量等.
2、向量的表示
A
B
1、字母表示:AB或a
2、坐标表示:
x
y
O
(x,y)
A
x
y
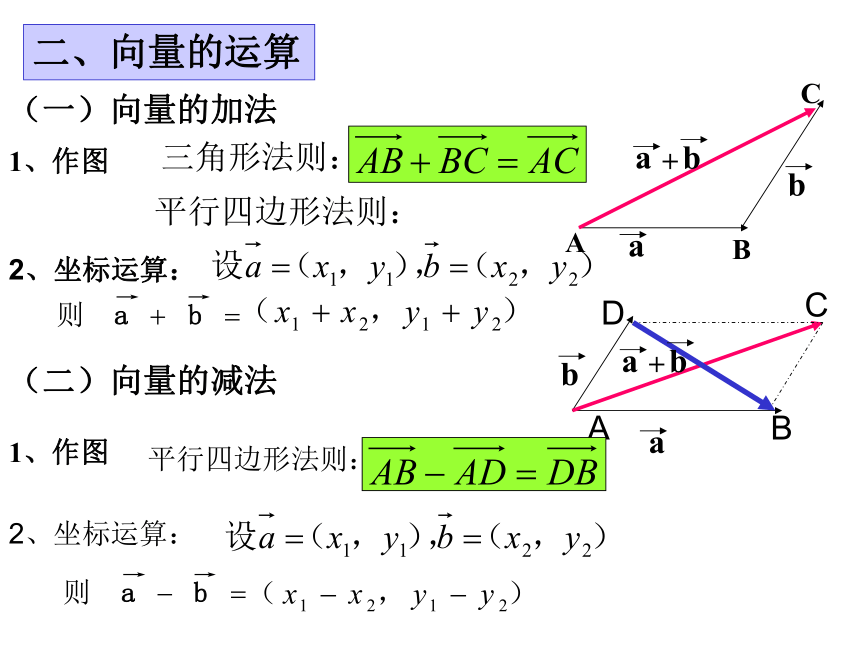
二、向量的运算
(一)向量的加法
A
B
C
三角形法则:
A
B
C
D
平行四边形法则:
a
b
2、坐标运算:
1、作图
(二)向量的减法
2、坐标运算:
1、作图
平行四边形法则:
a
b
a
b
+
a
b
+
(1)长度:
(2)方向:
(三)数乘向量
5、平面向量基本定理
向量
与非零向量
共线
有且只有一个实数
,使得
=
。
4、共线向量基本定理
1、平面向量数量积的定义:
2、数量积的几何意义:
O
A
B
θ
B1
(四)
数量积
4、运算律:
3、数量积的坐标运算
五、向量垂直的判定
六、向量平行的判定(共线向量的判定)
七、向量的长度
八、向量的夹角
向量表示
坐标表示
向量表示
坐标表示
C
-3
解:∵
∴
同理可得
∴θ=120°
2
1
2
2
2
1
1
1
2
1
PP
P
P
y
x
P
y
x
P
P
P
y
x
P
l
l
=
即
)
,
(
),
,
(
,其中
所成定比为
)分有向线段
,
(
点
定比分点P的坐标
中点坐标
九、线段的定比分点
十、平移公式
知二求一
重心坐标
十一、正弦余弦定理
(R为外接圆半径)
2R
两边一对角
两角任一边
两边一夹角
三边
1、正弦定理:
2、余弦定理:
c2=a2+b2-2abcosC
b2=c2+a2-2cacosB;
a2=b2+c2-2bccosA;
cosC=
cosB=
cosA=
内角和定理:
A+B+C=180°,sin(A+B)=sinC,
cos(A+B)=
-cosC,
cos
=sin
sin
=cos
面积公式:
S=
absinC=
bcsinA=
casinB
3
一、向量的基本概念
向量、零向量、单位向量、共线向量(平行向量)、相等向量、相反向量等.
2、向量的表示
A
B
1、字母表示:AB或a
2、坐标表示:
x
y
O
(x,y)
A
x
y
二、向量的运算
(一)向量的加法
A
B
C
三角形法则:
A
B
C
D
平行四边形法则:
a
b
2、坐标运算:
1、作图
(二)向量的减法
2、坐标运算:
1、作图
平行四边形法则:
a
b
a
b
+
a
b
+
(1)长度:
(2)方向:
(三)数乘向量
5、平面向量基本定理
向量
与非零向量
共线
有且只有一个实数
,使得
=
。
4、共线向量基本定理
1、平面向量数量积的定义:
2、数量积的几何意义:
O
A
B
θ
B1
(四)
数量积
4、运算律:
3、数量积的坐标运算
五、向量垂直的判定
六、向量平行的判定(共线向量的判定)
七、向量的长度
八、向量的夹角
向量表示
坐标表示
向量表示
坐标表示
C
-3
解:∵
∴
同理可得
∴θ=120°
2
1
2
2
2
1
1
1
2
1
PP
P
P
y
x
P
y
x
P
P
P
y
x
P
l
l
=
即
)
,
(
),
,
(
,其中
所成定比为
)分有向线段
,
(
点
定比分点P的坐标
中点坐标
九、线段的定比分点
十、平移公式
知二求一
重心坐标
十一、正弦余弦定理
(R为外接圆半径)
2R
两边一对角
两角任一边
两边一夹角
三边
1、正弦定理:
2、余弦定理:
c2=a2+b2-2abcosC
b2=c2+a2-2cacosB;
a2=b2+c2-2bccosA;
cosC=
cosB=
cosA=
内角和定理:
A+B+C=180°,sin(A+B)=sinC,
cos(A+B)=
-cosC,
cos
=sin
sin
=cos
面积公式:
S=
absinC=
bcsinA=
casinB
3
